—Estoy preocupada —dijo la madre de Robert—. No sé lo que le pasa a este chico. Antes siempre estaba en el patio o en el parque, jugando al fútbol con Albert, Charlie, Enzio y los otros. Ahora está todo el día metido en su cuarto. En vez de hacer sus deberes, ha extendido en la mesa un gran pliego de papel y pinta liebres.
—Calla —dijo Robert—. Me confundes. Tengo que concentrarme.
—Y se pasa el día murmurando números, números, números. Eso no es normal.
Hablaba para sus adentros, como si Robert no estuviera en la habitación.
—Antes nunca se interesaba por los números. Al contrario, siempre se quejaba de su profesor por los deberes de matemáticas. Sal de una vez a tomar el aire —gritó por fin.
Robert levantó la cabeza de la hoja y dijo:
—Tienes razón. Si sigo contando liebres me dará dolor de cabeza.
Y Robert salió de casa. En el parque había una enorme pradera por la que no corría ni una sola liebre.
—Hola, Robert —gritó Albert al verle venir—. ¿Juegas?
También estaban Enzio, Gerardo, Ivan y Karol. Estaban jugando al fútbol, pero a Robert no le apetecía. No tienen ni idea de cómo crecen los árboles, pensó.
Cuando volvió a casa, era bastante tarde. Nada más cenar, se fue a la cama. Precavido, se metió un grueso rotulador en el bolsillo del pijama.
—¿Desde cuándo te vas tan pronto a la cama? —se sorprendió su madre—. Antes siempre querías quedarte lo más posible.
Pero Robert sabía muy bien lo que quería, y sabía también por qué no le contaba nada a su madre. No le hubiera creído cuando le hubiera dicho que las liebres, los árboles e incluso los moluscos saben contar, y que era amigo de un diablo de los números.
Apenas se había dormido cuando el anciano apareció.
—Hoy voy a enseñarte algo estupendo —dijo.
—Lo que sea, menos liebres. He pasado todo el día rompiéndome la cabeza con ellas. Siempre confundo las blancas y las pardas.
—¡Olvídalo! Ven conmigo.
Llevó a Robert hasta una casa blanca en forma de cubos. También dentro todo estaba pintado de blanco, incluso la escalera y las puertas. Llegaron a una gran habitación desierta, blanca como la nieve.
—Aquí ni siquiera puede uno sentarse —se quejó Robert—. ¿Y qué clase de ladrillos son esos?

Se acercó hasta el alto montón que había en la esquina y miró los ladrillos con más atención.
—Parece cristal o plástico —constató—. Grandes cubos. Dentro de ellos brilla algo. Tienen que ser filamentos eléctricos, o algo por el estilo.
—Electrónica —dijo el anciano—. Si quieres, construiremos una pirámide.
Cogió el primer par de cubos y los puso en fila en el blanco suelo.
—Ahora tú, Robert.
Siguieron construyendo hasta que la fila tuvo el siguiente aspecto:

—¡Alto! —gritó el diablo de los números—. ¿Cuántos cubos tenemos ahora?
Robert contó.
—Diecisiete. Pero es una cifra coja —dijo.
—No tan coja como tú piensas. Sólo tienes que restarle uno.
—Dieciséis. Otra vez un número saltado. Un dos saltado cuatro veces: 24.
—Fíjate —dijo el anciano—. Te das cuenta de todo. Pero ahora sigamos construyendo. El siguiente ladrillo se pone siempre sobre la grieta entre los dos anteriores, exactamente igual a como hacen los albañiles.
—O. K. —dijo Robert—. Pero esto nunca llegará a ser una pirámide. Las pirámides tienen tres o cuatro esquinas en la base, y esta cosa es plana. Esto no se convertirá en una pirámide, sino en un triángulo.
—Bien —dijo el diablo de los números—. Entonces construiremos un triángulo.
Y siguieron hasta que estuvo listo.

—¡Listo! —gritó Robert.
—¿Listo? Ahora es cuando empieza lo bueno.
El diablo de los números trepó por un lado del triángulo y escribió un uno en el cubo más alto.
—Como siempre —murmuró Robert—: ¡tú y tus unos!
—¡Claro! —respondió el anciano—. Todo empieza en el uno. Ya lo sabes.
—Pero ¿cómo sigue?

«Parece cristal o plástico», constató Robert. «Grandes cubos. Dentro brilla algo. Tienen que ser filamentos eléctricos o algo por el estilo».
—Enseguida lo verás. En cada uno de los otros cubos escribiremos lo que resulte de sumar lo que hay encima.
—Una obra de arte —dijo Robert.
Sacó del bolsillo su grueso rotulador y escribió:
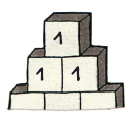
—Nada más que unos —dijo—. Hasta hoy soy capaz de hacerlo incluso sin calculadora.
—Enseguida serán más. Sigue —gritó el diablo de los números, y Robert escribió:
—Un juego de niños —dijo.
—No seas tan arrogante, querido. Espera a ver cómo sigue.
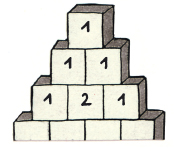
Robert calculó y escribió:
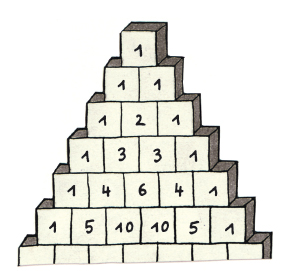
—Ya veo, las cifras al borde son unos, no importa lo abajo que lleguemos. Y las de al lado en diagonal también puedo escribirlas enseguida, son sencillamente los números normales: 1, 2, 3, 4, 5, 6, 7…
—¿Y qué pasa con la siguiente diagonal, la que está justo al lado de 1, 2, 3, 4, 5, 6, 7…? Lee las primeras cuatro cifras —el diablo de los números había vuelto a poner su sonrisa astuta, y Robert leyó de arriba a la derecha abajo a la izquierda:
—1, 3, 6, 10… Me suenan familiares.
—Cocos, cocos —gritó el anciano.
—¡Ah, sí!, ahora me acuerdo. 1, 3, 6, 10… son los números triangulares.
—¿Y cómo se hacen?
—Por desgracia lo he olvidado —dijo Robert.
—Muy sencillo:
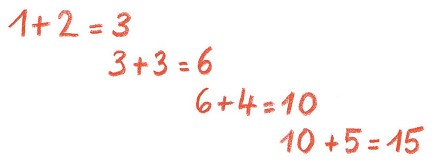
—… 15 + 6 = 21 —prosiguió Robert.
—¡Ahí lo tienes!
De esa forma, Robert escribió cada vez más números en los cubos. Por una parte, la cosa era cada vez más fácil, porque ya no tenía que estirarse tanto, pero, por otra, las malditas cifras se volvían cada vez más elevadas.
—¡Ehhh! —dijo—. No puedes pedirme que calcule todo eso de cabeza.
—Como tú digas —contestó el anciano—. Pero no te excites. ¡Que todo esto se vaya al diablo si no lo hago en un abrir y cerrar de ojos!
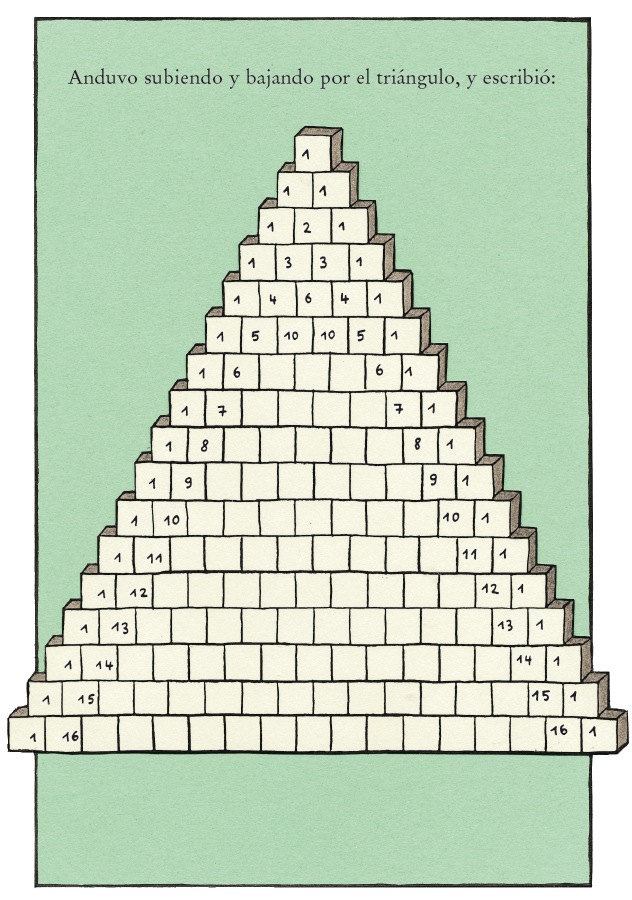
Y, a un ritmo de locos, escribió el triángulo entero.
—Ahí abajo se vuelve un rato estrecho —dijo Robert—. ¡12870! ¡Qué auténtico!
—Oh, eso son pequeñeces. Hay aún mucho más en este triángulo.

¡Así es! Quizá creáis que esto sólo sirve para romperse la cabeza. ¡Falso! Lo contrario es lo que es cierto. Es cosa de gente vaga, a la que no le gusta hacer muchas cuentas. Si, por ejemplo, queréis saber qué sale al sumar los doce primeros números triangulares, sólo tenéis que coger la tercera fila en diagonal a la derecha hacia abajo, la que empieza con 1, 3, 6, 10. Seguid con el dedo hasta el cubo número doce de esta fila. Luego buscad el número que está justo debajo a la derecha. ¿Cuál es? De este modo os habréis ahorrado calcular cuántos son 1 + 3 + 6 + 10 + 15 + 21 + 28 + 36 + 45 + 55 + 66 + 78.
»¿Sabes lo que hemos construido? —preguntó el diablo de los números—. ¡Esto no es un simple triángulo, es un monitor! Una pantalla. ¿Por qué crees que todos los cubos tienen vida electrónica interior? Sólo tengo que conectar esta cosa y se iluminan.
Dio unas palmadas y la habitación se oscureció. Luego dio otra más, y el cubo de arriba del todo se iluminó en rojo.

—Otra vez el uno —dijo Robert.
Cuando el anciano volvió a dar palmas, la primera línea se apagó y la segunda brilló como un semáforo que pasa a rojo.
—Quizá puedas sumarla —dijo.
—1 + 1 = 2 —murmuró Robert—. ¡No es que sea precisamente sensacional!
El diablo de los números dio otra palmada, y la tercera línea se volvió roja.
—1 + 2 + 1 = 4 —exclamó Robert—. No hace falta que sigas dando palmadas. Ya lo he entendido. Se trata de nuestros viejos conocidos, los doses saltarines. La siguiente línea sale 2 x 2 x 2 o 23, igual a 8. Etcétera: 16, 32, 64. Hasta que el triángulo termina por abajo.
—La última línea —dijo el anciano— da 216, y eso es bastante: 65.536, por si quieres saberlo con exactitud.
—¡Mejor que no!
—Está bien —el diablo de los números batió palmas, y volvió a hacerse la oscuridad.
—¿Quieres volver a ver a unos cuantos viejos conocidos? —preguntó.
—Depende.
El anciano dio tres palmadas, y los cubos volvieron a iluminarse: algunos en amarillo, otros en azul, los siguientes en verde o rojo.
—Parece carnaval —dijo Robert.
—¿Ves las escalerillas del mismo color que van de arriba a la derecha hasta abajo a la izquierda?

Vamos a sumar todo lo que sale en una de ellas, y veremos qué sale. ¡Empieza con la roja, arriba del todo!
—Sólo tiene un escalón —dijo Robert—. Uno, como siempre.
—Luego, la amarilla de debajo.
—Tampoco tiene más que uno: uno.
—La próxima es una azul. Dos cubos.
—1 + 1 = 2.
—Luego la verde, justo debajo. Dos cubos verdes.
—2 + 1 = 3.
Ahora Robert sabía cómo seguir:
—Otra vez rojo: 1 + 3 + 1 = 5. Y amarillo: 3 + 4 + 1 = 8. Azul: 1 + 6 + 5 + 1 = 13.
—¿Qué podría significar: 1, 1, 2, 3, 5, 8, 13…?
—¡Bonatschi, naturalmente! Los números de las liebres.
—Ya ves que todo está en nuestro triángulo. Podríamos seguir durante días, pero creo que tienes suficiente por hoy.
—Puedes decirlo bien fuerte —admitió Robert.
—Está bien, basta de cálculos.
El diablo de los números batió palmas, y los cubos de colores se apagaron.
—Pero nuestro monitor aún es capaz de hacer muchas más cosas. Si vuelvo a batir palmas, ¿sabes lo que ocurrirá? Se iluminarán los números pares en todo el triángulo, y los impares seguirán oscuros. ¿Quieres que lo haga?

—Por mí…
Lo que Robert vio entonces fue una auténtica sorpresa.
—¡Es una locura! Un dibujo. Triángulos dentro del triángulo, sólo que cabeza abajo.
Robert estaba fuera de sí.
—Mayores y menores —dijo el diablo de los números—. Sin duda el pequeño parece un cubo, pero en realidad es un triángulo. El mediano consta de 6 cubos, y el grande de 28. Naturalmente, son números triangulares.
»Así que ahora sólo brillan en amarillo los números pares. ¿Qué crees que pasará si encendemos todos los números de nuestro monitor que se puedan dividir entre tres, cuatro o cinco? Sólo tengo que dar una palmada y lo verás. ¿Con qué divisor lo intentamos, con el cinco?
—Sí —dijo Robert—. Todos los que se puedan dividir entre cinco.
El anciano dio una palmada, las cifras amarillas se apagaron y las verdes se encendieron.

—Es increíble —dijo Robert—. Otra vez triángulos, pero ahora son otros. ¡La más pura brujería!

—Sí, querido, a veces yo mismo me pregunto dónde terminan las Matemáticas y dónde empieza la brujería.
—Fantástico. ¿Has inventado tú todo esto?
—No.
—¿Quién ha sido entonces?
—¡Sabe el Diablo! El gran triángulo de números es una cosa antiquísima, mucho más vieja que yo.
—Pues a mí me pareces bastante viejo.
—¿Yo? Permite que te diga que soy uno de los más jóvenes del paraíso de los números. Nuestro triángulo tiene por lo menos dos mil años. Creo que la idea se le ocurrió a algún chino. Pero hoy aún seguimos dándole vueltas, y seguimos hallando nuevos trucos que se pueden hacer con él.
Si seguís así, pensó Robert para sus adentros, es posible que no acabéis nunca. Pero no lo dijo. Sin embargo, el diablo de los números le había entendido.
—Sí, las Matemáticas son una historia interminable —dijo—. Hurgas y hurgas y siempre encuentras cosas nuevas.
—¿No podéis dejar de hacerlo nunca? —preguntó Robert.

—Yo no, pero tú sí —susurró el diablo de los números, y cuando lo dijo los cubos verdes se hicieron cada vez más pálidos y él mismo se volvió cada vez más delgado, hasta que se quedó igual que un fideo y con cara de pito. La habitación estaba oscura como boca de lobo, y pronto Robert lo hubo olvidado todo, los cubos de colores, los triángulos, los números de Bonatschi e incluso a su amigo, el diablo de los números.

Durmió y durmió, y cuando despertó a la mañana siguiente su madre le preguntó:
—Estás muy pálido, Robert. ¿Has tenido pesadillas?
—Nooo —dijo Robert—. ¿Por qué?
—Estoy preocupada.
—Pero, mamá —respondió Robert—, ya sabes lo que dicen: No hay que mentar al Diablo.

¿Alguno de vosotros quiere saber qué dibujo sale cuando se iluminan todos los números del monitor que se pueden dividir entre cuatro? ¡Adelante! Para eso no hace falta ser ningún diablo de los números. ¡Cualquiera de vosotros puede hacerlo! Coged un lápiz de colores y pintad todos los números que salen en la tabla del cuatro. Cuando los números os resulten demasiado grandes, utilizad una calculadora. Simplemente coged el número, pulsad los signos: 4, y veréis si sale. En la página siguiente está el triángulo.
