Escribe los números del 0 al 9 en una hoja de papel. Subraya cinco de esos números. Con los dígitos que has subrayado, utilizándolos en cualquier orden, forma un número de 5 cifras. Ahora, con los 5 dígitos que no has utilizado forma otro número de 5 cifras. Suma los dos números que has construido y rodea una de las cifras del resultado, una cifra que no sea un nueve. Suma ahora todos los dígitos del resultado menos el que no has rodeado. Si el resultado es un número de dos cifras, suma estas dos hasta que te quede un solo dígito. Resta a 9 el dígito que te ha quedado. Comprueba que el resultado ahora coincide con la cifra que habías rodeado.
El 9 simboliza el amor y la gestación (en humanos, ésta dura 9 meses). También es el cuadrado del primer número impar.
La prueba del 9
Entre las cosas que hemos aprendido en la asignatura de matemáticas cuando éramos pequeños, está la prueba del 9. Puede que nos pareciera absurdo hacerla, sobre todo cuando no nos equivocábamos en las operaciones, pero un sistema matemático parecido a esa prueba se utiliza hoy en casi todos los comercios, y tiene que ver con el sistema de lectura de los códigos de barras. En el capítulo segundo nos ocupábamos del sistema de numeración en base 2, y en el séptimo hablábamos de la aritmética módulo 7. Hacer la prueba de los nueves es equivalente a calcular el resto módulo 9 y verificar la operación para esos restos. Tomemos un número al azar: por ejemplo 50; si dividimos 50 entre 9 nos queda como cociente 5 y como resto también 5. Curiosamente, la suma de los dígitos que componen el número 50 es 5. Tomemos otro número como ejemplo: 2153. Al dividirlo entre 9, el cociente es 239 y el resto 2. La suma de los dígitos que componen 2153 es 2 + 1 + 5 + 3 = 11. Si continuamos sumando los dígitos que componen 11, obtenemos 1 + 1 = 2, precisamente, el resto que se obtenía al dividir por 9. No vamos a probar por qué esto es así, pero es una consecuencia sencilla de que el sistema de numeración que utilizamos es el de base 10 y de que 9 = 10 – 1. Un número es múltiplo de nueve cuando la suma de las cifras que lo componen es también múltiplo de 9.
Las operaciones habituales de la aritmética se conservan cuando consideramos la aritmética modular. Así, si tomamos la suma de 111 y 587 (que es 698), dividimos entre 9 y calculamos el resto, veremos que éste es 5. Nos habría dado igual haber calculado primero los restos que se obtienen al dividir 111 entre 9 (el resto es 3) y 587 entre 9 (el resto es 2) y haber sumado esos restos. Esta propiedad que he expuesto aquí con esos números concretos se extiende a cualesquiera otros números; recordemos, por ejemplo, la aritmética módulo 7 estudiada en el séptimo capítulo, en la que 6 + 4 = 3 o, equivalentemente, sábado + 4 = miércoles.
La aplicación más común de la prueba del 9 aparece en las divisiones. La prueba del 9 no nos garantiza que la operación esté bien hecha, pero lo que sí permite detectar es cuándo nos hemos equivocado. Recordemos que siempre se tiene que el dividendo es igual al divisor multiplicado por el cociente más el resto. Esa misma relación se tiene que verificar para los restos módulo 9; cuando no es así, se deduce que la división está mal hecha.
Veamos con un ejemplo el funcionamiento de la prueba del 9. Supongamos para ello que queremos dividir 25396 entre 48. El cociente es 529 y el resto, 4 unidades. Los restos módulo 9 para 25396, 48, 529 y 4 son, respectivamente, 7, 3, 7 y 4, calculados de la manera que hemos enseñado antes: sumando los dígitos que componen esos números. Observamos que 3 x 7 + 4 = 25; 5 + 2 = 7; y ese valor, 7, es justamente el resto que queda al dividir 25396 entre 9, que es lo que cabía esperar. Supongamos que nos hemos equivocado al dividir y nos resulta que el cociente es 46 en vez de 48; el resto de la división de 46 entre 9 es 1 (4 + 6 = 10; 1 + 0 = 1). Al aplicar la fórmula «divisor por cociente más resto» para los restos módulo 9, nos resulta: 1 x 7 + 4 = 11 = 2 (módulo 9). Si la operación hubiera sido correcta, debería haber resultado 7 en lugar de 2, lo que nos indica que nos hemos equivocado en la división.
 Triángulo numérico
v.1.0
Triángulo numérico
v.1.0
Veremos una primera versión de una aplicación de la aritmética modular a la magia. Tras la primera descripción del juego, en la que se intenta que sea una sorpresa para el lector, proporcionaré otra versión, para hacer el juego a otras personas.
1. Escribe 10 cifras en fila, una a continuación de otra.
2. Calcula la suma de cada par de dígitos adyacentes. Si te queda un número de dos cifras, suma esas cifras hasta que te haya quedado reducido a un único dígito. Escríbelo debajo de los dos números de los que proviene, en una fila aparte.
3. Continúa realizando el mismo proceso con cada una de las filas que se van formando en cada paso.
4. Cuando llegues a un solo número, apúntalo en una hoja de papel.
5. Por otra parte, calcula la suma de la cuarta y la séptima cifra de las que escribiste al principio. Multiplica ese resultado por 3 y redúcelo a un dígito sumando las cifras que lo componen.
6. Al resultado de la operación anterior súmale el primer y el décimo dígito de los que escribiste. Reduce todo ese resultado a una cifra.
7. Comprueba que has llegado al número que habías apuntado en el papel.
Para poder seguir mejor los pasos que acabo de describir pondré un ejemplo: supongamos que inicialmente partimos de los 10 números 2, 4, 2, 1, 0, 6, 7, 3, 5 y 8. El proceso de sumar dos adyacentes, calcular el resto módulo 9 (precisamente eso es lo que estamos haciendo cuando pedíamos reducir a un solo dígito el número sumando las cifras que lo componían) y escribir ese resultado en otra fila nos da lugar a un triángulo numérico. Para los dígitos que he elegido como ejemplo, la segunda fila empezará por 6 = 2 + 4, 6 = 4 + 2, 3 = 2 + 1... (recordemos que cada número de la segunda fila es la suma de los dos que se encuentran justo encima de él; y que cuando resulta un número de dos cifras hay que sumar éstas, para reducirlas a un único dígito). Haciendo todas las operaciones, nos resulta el siguiente triángulo:

Por otra parte, la suma de las cifras cuarta y séptima es 8, lo que multiplicado por 3 es 24; y reducido a un solo dígito, 6. Si sumamos a ese número las cifras primera y última, nos queda 16; y, al calcular el resto módulo 9, obtenemos finalmente como resultado 7, que coincide con lo que arrojan todas las operaciones que hemos realizado en el triángulo.
Éste es un bonito juego de mentalismo. Al ejecutarlo (y aquí es donde viene la versión 1.1) conviene pedir al espectador que escriba en una fila diez cifras y, a la vista de lo que escriba, hacer los pasos 5 y 6 del procedimiento anterior, calculando mentalmente. El resultado de hacer las operaciones descritas en los pasos 5 y 6 lo escribimos en una hoja y la doblamos, a modo de predicción, la dejamos en un lugar visible y no volvemos a acercarnos a ella. Mientras tanto, el espectador irá completando las filas del triángulo. ¿El lector se hace una idea de por qué puede ser esto así?
 Triángulo numérico
v.2.0
Triángulo numérico
v.2.0
Este juego es similar al anterior, pero se hace más vistoso porque para su realización se utilizan naipes. Emplearemos únicamente las cartas cuyos valores están comprendidos entre el 1 y el 9 (ambos incluidos). Tomaremos cartas de los cuatro palos de la baraja para construir una pirámide de cartas como la representada en la figura 65.
El espectador debe mezclar las cartas y coger cinco de ellas
para formar la base de la pirámide. A partir de las cartas de la
primera fila construiremos la segunda. Si observamos la figura, nos
daremos cuenta de que sobre cada par de cartas adyacentes se ha
situado otra, cuyo valor es la suma de las dos cartas inferiores
reducido a un solo dígito (si fuera un número de dos cifras, se
suman éstas, tal como ya hemos hecho en el juego anterior). Debemos
calcular dónde va a quedar el vértice de la pirámide y allí
situaremos una carta boca abajo, que nos servirá de predicción. La
carta situada boca abajo puede ser determinada mediante una simple
operación aritmética: si esas cinco cartas son 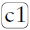



 , se calcula el valor de la
carta haciendo
, se calcula el valor de la
carta haciendo 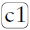 + 4 x
+ 4 x  + 6 x
+ 6 x  + 4 x
+ 4 x  +
+  y sumando los dígitos que componen ese número
hasta que nos quedemos con una única cifra.
y sumando los dígitos que componen ese número
hasta que nos quedemos con una única cifra.
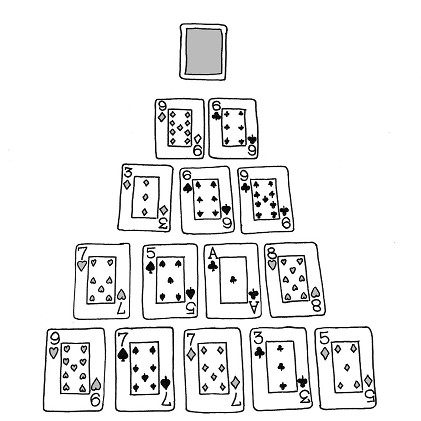
FIGURA 65. Pirámide de cartas.
Existe una forma sencilla para realizar la operación que nos proporcionará la predicción: reducir los números a un único dígito en cada paso que hagamos y considerar los nueves como ceros. ¿No se entiende? Hacer los cálculos para el ejemplo propuesto ayudará: si hiciéramos todas las operaciones, deberíamos computar 9 + 4 x 7 + 6 x 7 + 4 x 3 + 5 = 96. Sumando las cifras del resultado obtenemos 9 + 6 = 15; y, como este número sigue teniendo dos cifras, volvemos a repetir la operación: 1 + 5 = 6. El método rápido para hacer ese cálculo necesitaría únicamente realizar estos pasos: 0 + 1 + 6 + 3 + 5 =15; 1 + 5 = 6, que resulta mucho más sencillo, por ser más pequeños los valores que debemos sumar.
Los dos juegos de triángulos numéricos que se han descrito se basan tanto en la aritmética módulo 9 como en el triángulo de Tartaglia, que vuelve a entrar en escena. Si nos fijamos en cómo se llega al vértice, veremos que el proceso seguido es similar a la manera en que se construía el famoso triángulo. La forma como se hacen las «predicciones» se basa en los coeficientes binomiales. En el caso en el que comenzamos con 10 números, aparecen como coeficientes los números de la novena fila del triángulo de Tartaglia, que tienen la propiedad de ser todos múltiplos de 9, salvo el primero, el cuarto, el séptimo y el décimo, con lo que no aportarán nada a la suma cuando calculemos el residuo módulo 9. En la versión 2.0, en la que utilizamos las cartas, los coeficientes son 1, 4, 6, 4, 1: exactamente los que hemos utilizado.
Estos juegos permiten también volver a incidir en la idea de recurrencia: obtenemos unos valores en función de otros calculados ya previamente. Y si estiramos ese concepto, podemos hasta llegar a hablar del método de inducción matemática, que excede los límites que nos hemos propuesto aquí.
Códigos de barras
Recordar aquí el funcionamiento de la prueba del nueve no es gratuito. El hecho de comprobar la coherencia de los resultados que se obtienen es algo fundamental en el pensamiento matemático, ya se trate del resultado de una operación aritmética o de la solución a un problema práctico. Hace unos pocos años, cuando el uso de calculadoras y ordenadores no estaba tan extendido, era frecuente comprobar los resultados de las operaciones cada poco tiempo y ver si todo «cuadraba»; y para eso se empleaba. Hoy, diariamente se hace una comprobación similar por parte de las máquinas, pero esto pasa desapercibido: cuando vamos al supermercado y en la caja pasan nuestra compra por el lector de códigos de barras, se está comprobando que el lector de códigos ha funcionado bien. Al comprar un libro, vemos que tiene asignado un código universal ISBN, que también utiliza aritmética modular. Cuando damos nuestro número de DNI, tenemos también que dar la letra que determina el NIF. Lo que ocurría antes de implantar el uso de la letra en ese documento es que, si se producía lo que se llama coloquialmente un «baile de números» y que técnicamente es una transposición en los dígitos del DNI, se podía confundir a un contribuyente con otro; ahora, si la letra que se asigna no es la que tiene que corresponder con el resto de los dígitos, el sistema no admite ese DNI.
El juego con el que se ha abierto este capítulo utiliza el mismo principio. En efecto, pedíamos escribir los 10 dígitos del 1 al 9. La suma de esos 10 dígitos es 0 + 1 + 2 +…+ 9 = 45, que es múltiplo de 9, con lo que, al escribir dos números utilizando todos esos dígitos y sumar esos dos números, vamos a obtener un número que no sabremos cuál es, pero del que podemos asegurar que es múltiplo de 9, con lo que, al reducirlo a un solo dígito del modo que venimos haciendo, nos tiene que quedar 9; por consiguiente, la diferencia entre la suma de los números que no hemos elegido y 9 tiene que ser precisamente el número rodeado con una circunferencia.
La presentación habitual de este juego, para hacérselo a otras personas, es un poco diferente. Tras pedir que escriban dos números de cinco cifras y los sumen, debemos pedir que rodeen una cifra del resultado que no sea un cero. Se suele justificar que no rodeen esta cifra diciendo: «Como un cero no significa nada, rodea un número distinto de cero». A continuación, debemos pedir que nos digan, de uno en uno y en el orden que quieran, el resto de los dígitos del resultado. Mientras nos los dicen, los iremos sumando y reduciéndolos a un único dígito. Como el resultado final ha de ser múltiplo de 9, el número desconocido tiene que ser «lo que falta» para que lo sea. Si el número que nos queda tras reducir a un solo dígito es menor que 9, la cifra rodeada es la diferencia entre 9 y ese número. Si el número que nos ha resultado tras la reducción es un 9, el espectador podría haber rodeado un 0 o un 9; en ambos casos el resultado final sería múltiplo de 9; de ahí la prohibición de que rodee un 0 (o, en el ejemplo inicial, de que rodearas un 9). Si uno olvida este detalle, puede tener una situación complicada, como le ocurrió, en un programa de radio, a quien está escribiendo (era la primera vez que estaba en uno). Lo que podemos sacar de los errores es no volver a repetirlos; aunque si uno no los comete, ¡mejor!
Como indicaba antes, los programas asociados a los lectores de códigos de barras tienen también implementada una función de comprobación. Fijémonos en el código de barras de la figura 66, que corresponde a una lata de fabada asturiana. Podemos interpretar qué representa el código 8413000065504 gracias a un sistema normalizado de representación denominado EAN (European Article Number). En este sistema, los dos primeros dígitos identifican la organización a través de la cual se ha adscrito la empresa fabricante del producto al sistema EAN. El código de la organización que opera en España es 84; por eso el código de muchos productos españoles comienza por esos dígitos. El siguiente tramo de dígitos, que está constituido por un número comprendido entre 5 y 8 dígitos, identifica al propietario de la marca. Todos los dígitos que restan, salvo el último, representan el código de producto. Para calcular el último dígito, el llamado dígito de control, se suman las cifras del código de barras que ocupan las posiciones pares, se multiplica por 3 esta cantidad y se suman los dígitos de las posiciones impares (obviamente, sin considerar el dígito número 13: el propio dígito de control). Nos fijamos en el último dígito que nos ha quedado y lo restamos de 10; este último número que obtenemos es el dígito de control que sirve para comprobar que el escáner de códigos de barras ha efectuado una lectura correcta.

FIGURA 66. Un código de barras.
En nuestro ejemplo tenemos:
| 4 + 3 + 0 + 0 + 5 + 0 = 12 | Suma de los dígitos pares |
| 12 x 3 = 36 | Multiplicamos por 3 lo anterior |
| 8 + 1 + 0 + 0 + 6 + 5 = 20 | Suma de los dígitos impares |
| 36 + 20 = 56 | Suma de esas dos cantidades |
| 6 | Último dígito de la suma anterior |
| 10 – 6 = 4 | Dígito de control |
El proceso de verificación es mucho más sencillo: sólo hay que comprobar que el resultado de la suma de los dígitos que ocupan una posición par, multiplicada por 3, sumado, a su vez, a los dígitos que ocupan una posición impar sea un múltiplo de 10.
El cálculo de la letra que aparece en el NIF (Número de Identificación Fiscal) utiliza aritmética módulo 23. Se calcula el resto módulo 23 y al número resultante, comprendido entre 0 y 22, se le asigna una letra de acuerdo con la tabla siguiente:

 Nueve cartas
Nueve cartas
Para realizar este juego necesitamos 9 cartas con los 9 valores comprendidos entre el 1 y el 9. También será conveniente que en esas 9 cartas haya palos distintos. Por ejemplo, podemos elegir cartas rojas para los valores pares y negras para los impares. Si recordamos de qué palo es cada una de las cartas con las que vamos a trabajar, podremos lograr un efecto más sorprendente. En nuestro ejemplo trabajaremos con el as de tréboles, el 2 de diamantes, el 3 de tréboles, el 4 de corazones, el 5 de picas, el 6 de diamantes, el 7 de picas, el 8 de corazones y el 9 de tréboles.
1. Coloca las 9 cartas en la parte de arriba de la baraja.
2. Di que vas a hacer un juego con 9 cartas. Pide a un espectador que retire 9 cartas de la parte superior del mazo dejándolas sobre la mesa.
3. Pide al espectador que mezcle las 9 cartas. A partir de este momento te debes poner de espaldas al público.
4. Ahora, indica que reparta las cartas en tres hileras de tres cartas cada una.
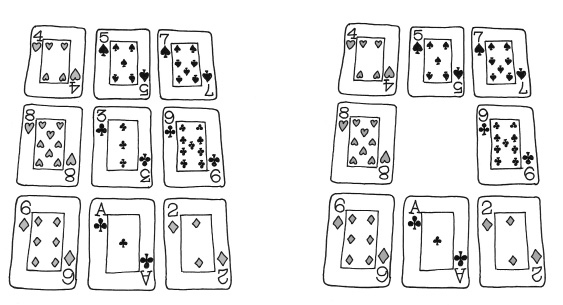
FIGURA 67. Nueve cartas al repartir; y después de retirar una.
5. Pide al espectador que coja una de las cartas y se la guarde en el bolsillo.
6. Pide que apunte los números que determinan cada una de las filas (en el ejemplo de la figura 67 los números serían: 457, 89 y 612).
7. Solicita al espectador que sume esos tres números.
8. Pide, por último, que te diga la suma de las cifras del resultado anterior.
9. Calcula el resto módulo 9 de la suma que te diga el espectador. Sustrae ese resto a 9. El número resultante indica el valor de la carta que ha retirado el espectador. El palo debes recordarlo.
Dejemos unos momentos para disfrutar del juego. El fundamento es exactamente el mismo que el del juego con el que se abría el capítulo o el de cómo se calcula el dígito de control en los códigos de barras o el ISBN. Tan sólo debemos tener en cuenta que en el juego se están empleando los 9 primeros números naturales, que su suma es múltiplo de 9 y que cualquier número que se construya utilizando todos ellos también ha de ser múltiplo de 9. Por todo ello, el valor de la carta que se oculta ha de coincidir con el complemento a 9 del número que nos indican (es decir, lo que le falta para que éste sea múltiplo de 9).
 El juego del 9
El juego del 9
Otra vez nos encontramos ante un juego en el que aparece el número 9. Para este juego necesitarás 24 monedas; forma con ellas un nueve, tal como se muestra en la figura 68, y reserva algunas para luego.
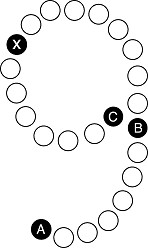
FIGURA 68. El juego del 9.
1. Piensa un número que sea mayor que 10.
2. Cuenta, desde la moneda marcada con una A en el dibujo, tantas monedas como indica el número que has pensado, de una en una y tocándolas con el dedo. Si el número que pensaste es tan grande como para que hayas llegado a C, a partir de ahí continúa dando vueltas dentro de la circunferencia del 9, hasta que termines de contar.
3. Una vez que has terminado la cuenta, vuelve a hacerla, pero ahora hacia atrás, comenzando por la misma moneda en la que terminaste la cuenta anterior. Si es necesario, puedes dar varias vueltas al círculo.
4. Marca con un lápiz o con un rotulador permanente la moneda en la que has terminado esta vez la cuenta.
5. Comprueba que se trata de la moneda representada con una X en la figura.
Si queremos hacer este juego delante de público, debemos hacer un ejemplo previo. Contamos de la forma descrita antes: primero, en sentido contrario a las agujas del reloj (sentido positivo para los matemáticos); y después en el sentido de las agujas del reloj (sentido negativo), siempre dando vueltas alrededor de la circunferencia que compone la parte superior del 9. Después de hacer las dos cuentas diríamos: «La moneda a la que habrías llegado sería ésta»; y señalas la marcada con una X. Si vuelves a hacer el juego tras el ejemplo, aunque cambies el número pensado, llegarías a la misma moneda. La clave está en cambiar el número de monedas que conforman la cola del 9.
En el ejemplo, la cola es el tramo de 8 monedas que empieza en A y termina en B. La moneda a la que llegamos, la marcada con X, es la octava si comenzamos a contar por C (en el sentido de las agujas del reloj). Si la cola tuviera 11 monedas, al final llegaríamos a la moneda que se encuentra a distancia 11 de C; y si la cola se redujese a sólo 5 monedas, todo el proceso terminaría en la quinta moneda. La idea aquí es otra que aparece en muchas demostraciones matemáticas y a la que ya nos hemos referido antes en este libro: si uno suma y resta la misma cantidad, lo que hace en realidad es dejar todo como estaba. Supongamos que reducimos la cola a 0 monedas. Al contar hacia adelante y luego hacia atrás, siempre estamos contando siguiendo la circunferencia y llegaríamos al punto donde hemos iniciado la cuenta. Al contar hacia adelante empezando por la cola y luego hacia atrás, siguiendo por la circunferencia, sin bajar por la cola, necesariamente terminaremos la cuenta en una posición «hacia atrás» equivalente al número de monedas de la cola.
Para realizar el juego, conviene cambiar el número de monedas que forman la cola del 9 en cada ejecución; así se terminará en monedas diferentes cada vez. También es conveniente que, cuando lo haga el espectador, tú te des la vuelta, le pidas que marque, por su cara oculta, la moneda en la que ha terminado la cuenta e inmediatamente tú vuelves a ponerte de cara al público y señalas la moneda a la que ha llegado.
 Una gran memoria
Una gran memoria
Terminaremos el capítulo con un juego de los que ensalzan la personalidad del mago. Aun cuando cualquier espectador puede darse cuenta de la agilidad manual que tiene un mago, en este juego realmente los que lo ven piensan que no hay ningún tipo de «truco» en su realización, sino que se debe a la gran memoria que posee quien lo hace. En realidad, no interviene para nada la memoria, sino una técnica y unas cuantas horas de ensayo hasta que se depura. La técnica está basada en la aritmética modular. Por comodidad, utilizaremos esta vez una baraja de 40 cartas, que puede ser una baraja española en la que asignaremos a las sotas, caballos y reyes los valores de 8, 9 y 10, respectivamente. Alternativamente, podemos utilizar una baraja francesa de la que hayamos retirado las figuras. También puede hacerse el juego con una baraja completa de 52 cartas, pero tendríamos que utilizar aritmética módulo 13 y resultaría más difícil su ejecución. Después lo comentaremos.
Comenzaremos recordando que el resto módulo 10 se calcula simplemente recordando el último dígito del correspondiente número. Recalco esto porque en el juego necesitaremos sumar valores de cartas y calcular el resto módulo 10 de los valores acumulados. Supongamos que la serie de valores que tenemos es 1, 10, 8, 3, 3, 4, 7, 2, 9. Las sumas que deberíamos ir haciendo mentalmente son 1 + 10 = 1; 1 + 8 = 9; 9 + 3 = 2; 2 + 3 = 5; 5 + 4 = 9; 9 + 7 = 6; 6 + 2 = 8; 8 + 9 = 7... Esta parte es muy sencilla y te recomiendo que, si tienes una baraja a mano, la mezcles y sumes, según el procedimiento que acabamos de mostrar, los valores de las 40 cartas del mazo. Recuerda que en la aritmética módulo 10 el número 10 es equivalente al 0, con lo que cada vez que aparezca un rey no debes sumar nada.
Si has concluido la suma anterior, habrás observado que el resultado final ha sido 0. Eso es porque la suma de valores de todas las cartas es múltiplo de 10. En efecto, la suma de valores de cada palo es 1 + 2 +… + 10 = 55; y, como hay 4 palos en la baraja, el total de valores es 55 x 4 = 220. Hagamos ahora un experimento: mezcla la baraja y esconde una carta (sin ver cuál es). Calcula la suma módulo 10 de los valores de las 39 cartas que quedan en el mazo (insisto, decir «suma módulo 10» parece una palabrota, pero es lo que hemos hecho antes: ir sumando valores y quedarnos sólo con el último dígito de la suma). ¿Ya tienes terminada la suma? ¿Te atreves a predecir cuál es el valor de la carta que has escondido? Si recuerdas todo lo que hemos hablado sobre el dígito de control en el código de barras EAN, y sabiendo que la suma de todas las cartas de la baraja es múltiplo de 10, puedes deducir que el valor de la carta escondida es 10 si la suma te ha quedado 0; y si la suma es un número s, entonces el valor de la carta escondida es 10 – s. Esta parte del juego no es demasiado complicada, pero necesita ser ensayada.
De momento, ya tenemos el procedimiento para calcular el valor de la carta escondida. Ahora nos hace falta un método para determinar el palo. Si hubiera sólo dos palos en la baraja, también sería sencillo conocer el palo basándonos en la paridad del número de cartas de un determinado palo mediante un procedimiento similar al que utilizábamos al contar el número de vueltas que dábamos a las monedas en el capítulo 2. Supondremos a partir de ahora que nos encontramos sentados y diremos que un movimiento del pie es levantarlo por los pulgares o bajarlo, si es que está levantado; así, si movemos el pie izquierdo cada vez que veamos una carta de oros o copas y no lo movemos cuando sea de espadas o bastos cuando hayamos visto las 39 cartas, deduciremos que si el pie izquierdo está en la posición inicial de reposo la carta escondida era de espadas o bastos, puesto que se ha producido un número par de movimientos del pie. Si los pulgares del pie izquierdo terminan levantados, quiere decir que ha habido un número impar de movimientos, de forma que la carta que falta es de oros o copas. ¿Comprendido?
Con lo que acabo de describir no hemos solucionado el problema por completo, porque tenemos cuatro palos en la baraja. Lo que vamos a hacer es combinar dos veces el mismo procedimiento (ésta es otra idea matemática muy importante) y lo que haremos será mover el pie izquierdo cada vez que veamos una carta de oros; el derecho, cada vez que veamos una de copas; los dos pies, cada vez que veamos una de espadas; y ninguno, cuando la carta que pasemos sea de bastos. Esta parte del juego necesita una importante coordinación de los miembros, ya que las manos pasan cartas, los ojos la miran, el cerebro procesa y los pies deben moverse según el palo que estemos viendo. Si quieres, puedes hacer de nuevo un ensayo: coge la baraja (completa, con 40 cartas), mézclala, esconde una carta sin ver cuál es y comienza a mirar el resto de las cartas de una en una, haciendo movimientos en los pies dependiendo de los palos. Cuando hayas concluido, puedes llegar a una de estas cuatro situaciones:
| Pie izquierdo levantado | OROS |
| Pie derecho levantado | COPAS |
| Los dos pies levantados | ESPADAS |
| Los dos pies en reposo | BASTOS |
Comprueba ahora el palo de la carta escondida y si has realizado correctamente los movimientos. Es posible que no te quede todo como esperabas, pero ése es un fallo de ejecución, no de las matemáticas en las que se basa el juego. Este juego necesita mucho ensayo, pero el esfuerzo merece la pena.
El porqué de la tabla anterior es fácil de comprender: si se termina con el pie izquierdo o el derecho levantado, como sabemos que sólo hay uno de los palos con un número impar de cartas, ello quiere decir que el número de cartas vistas de oros o copas, respectivamente, ha sido impar. Si los dos pies están en reposo, quiere decir que el número de copas, oros y espadas ha sido par, con lo que el impar ha de ser el de bastos. Si los dos pies están levantados, es porque el número de cartas de espadas vistas ha sido impar. Insisto en que es fundamental que la baraja esté completa y en que es muy importante ensayar previamente el juego, ya que hay que combinar ambos procedimientos: el de los pies para la determinación del palo y el de las sumas módulo 10 para el cálculo del valor de la carta.
Un método alternativo para deducir el palo de la carta escondida es el que me sugirió un profesor del IES Infanta Elena de Jumilla, en Murcia. Él era jugador de tute y está acostumbrado a tener en cuenta las cartas que han ido saliendo (claro, es importante al final de cada juego quién se lleva las diez de monte). Cada palo de la baraja española tiene las cartas enmarcadas de un modo diferente: los oros aparecen rodeados por un rectángulo continuo, mientras que el marco de las copas aparece con un hueco en medio en la parte superior y la inferior, quedando partido el marco en 2 trozos. Las espadas tienen dos huecos y los bastos tres. Así, contando el número de huecos de la parte superior de las cartas podemos saber cuál es el palo de la carta que falta.
En efecto, el total de huecos es 10+20+30=60 (recordemos que los oros no presentan un espacio, las copas tienen uno, espadas dos y bastos tres, además hay 10 cartas de cada uno de estos palos). Y ese número, 60, es múltiplo de 4. Si la carta escondida es de oros no aportará huecos: el resultado de contar todos seguirá siendo 60. Si la carta escondida es de copas el total sería 59, si es de espadas 58 y si es de bastos 57.
Pero es que se puede simplificar esta cuenta, trabajando con aritmética módulo 4 (recordamos: dividir entre 4 y quedarnos con el resto). Para llevar el conteo en módulo 4 basta con restar 4 al número que tengamos cada vez que supere este valor. Así, por ejemplo, el 4 es equivalente a 0, 5 equivalente a 1, 6 a 2 y 7 a 3. Sumar estos números es mucho más sencillo. De este modo, si el resultado final al contar todos los huecos es 0, la carta será de oros, si es 3 será de copas (claro, falta 1 para que el resultado sea 0 y esa es la carta escondida), si es 2 será de espadas y si es 1 será de bastos (faltarían 3 para llegar a 0).
Describamos, a modo de resumen, el procedimiento a emplear en este juego:
1. Comienza el juego haciendo gala de tus aptitudes memorísticas, que te permiten recordar los valores de todas las cartas de la baraja.
2. Entrega la baraja a un espectador. Pídele que la mezcle a fondo, que corte y, si quiere, que la vuelva a mezclar. Lo que interesa es que se convenza de que la baraja está mezclada.
3. Pide al espectador que retire una carta y se la guarde sin mirarla. Te debe entregar el resto de la baraja.
4. Recuerda que posees una gran memoria, que una persona normal sería incapaz de recordar qué carta falta en el mazo viendo una única vez cada carta. Si quieres, puedes invitar a alguien a intentarlo.
5. Emplea el procedimiento descrito para el cálculo del valor de la carta y del palo. Tranquilamente y sin equivocarte. Tómate tu tiempo.
6. Pide al espectador que saque la carta que se había guardado. Que vea él sólo cuál es, sin decírselo a nadie.
7. Anuncia cuál es la carta y pide al espectador que la muestre.
Como ves, el juego es completamente automático, pero necesita ensayo. El público no va a creer que hay esas matemáticas debajo del juego, sino que realmente eres capaz de recordar todas las cartas que has ido viendo y cuál es la que falta, con lo que pensarán en tus capacidades mentales. Recuerda que no debes realizar el juego ante público sin tenerlo completamente dominado.
Un último comentario, por si quieres hacer el juego con una baraja completa francesa de 52 cartas. Todo cambia, aunque sigue siendo lo mismo: la aritmética que hay que emplear es aritmética módulo 13, que es mucho más difícil de llevar «de cabeza». Para la misma secuencia que utilizábamos antes: 1, 10, 8, 3, 3, 4, 7, 2, 9, las sumas ahora serán: 1 + 10 = 11; 11 + 8 = 6; 6 + 3 = 9; 9 + 3 = 12; 12 + 4 = 3; 3 + 7 = 10; 10 + 2 = 12; 12 + 9 = 8. A los reyes se les asigna el valor 13, que es equivalente al valor nulo en la aritmética módulo 13. Con ensayo, también se puede usar esta versión. Con los palos ocurre algo parecido: ahora, el número de cartas en cada palo es impar, con lo que, utilizando el orden «picas, corazones, tréboles y diamantes» y las acciones respectivas de «mover pie izquierdo, mover pie derecho, mover ambos pies, no hacer nada», llegamos a estas situaciones:
| Pie izquierdo levantado | PICAS |
| Pie derecho levantado | CORAZONES |
| Los dos pies levantados | TRÉBOLES |
| Los dos pies en reposo | DIAMANTES |
En efecto, aunque parezca extraño, la tabla es similar a la anterior, una vez más por un problema de paridad: si la carta oculta es de picas, moveremos el pie izquierdo un número par de veces por cada vez que veamos picas y un número impar por las 13 cartas de tréboles, con lo que resulta un número impar (el pie derecho estará en la posición de reposo por haber sido movido 26 veces: 13, correspondientes a los corazones; y 13, a los tréboles).
Razonamientos similares permiten completar la tabla.