6 Limits: Imperfect Programs
Up until now, we’ve considered only small ideal programs and processes. Starting in this chapter, we take the first step toward a more realistic view by understanding some of the limits the universe imposes on the construction and running of processes. In this chapter we take up various ways in which processes are flawed, while in the next chapter we consider the limits even when processes are perfect. However, both chapters assume only a single process running on correctly functioning step-taking machinery. In later chapters we’ll encounter still another set of problems caused by multiple processes (chapter 8) or by failures (chapter 16).
All Software Is Flawed
Professional programmers tend not to criticize each other solely for the presence of flaws in programs. It would be strange for company A to criticize company B’s software product simply because company B had published a list of known problems with its product—because the reality is that company A’s software product almost certainly has a roughly similar list of known problems. Can we ever expect to have software that is free of flaws? Today, that is not a realistic expectation. What we can hope—but cannot guarantee—is that the flaws are not serious. Even that condition is sometimes hard to achieve, and it’s worth understanding why.
There are program design techniques to help us make programs that are easier to understand, and there are tools that can help us to identify likely sources of error; but the normal state of software is that it contains some errors (sometimes called “bugs”) and accordingly can fail to meet the expectations of its users.
This acceptance of bugs often comes as a surprise to people who are not programmers. Some of the problems are caused by bad practices in the software industry, but most of them are related to the fundamental nature of software—and so they’re not likely to go away any time soon.
In this chapter we take up four key problems that lead to software flaws:
- 1. Use of discrete states
- 2. Massive scale of state changes
- 3. Malleability
- 4. Difficulty of accurately capturing requirements and building corresponding implementations
The next chapter considers some additional problems that arise even when software is not flawed. But for the rest of this chapter, we take up each of these flaw-producing issues in turn. These problems are limits imposed by reality; we might consider them to be the hazards imposed by our inability to have perfect computation.
Discrete States
Let’s first consider that the use of discrete states can itself be a source of error. We’ve previously looked at the digital nature of both data and action in the world of software and processes (chapters 2 and 3). A digital view of the world sees it as composed of discrete levels of value; in contrast, an analog view of the world sees it as composed of continuous, smoothly varying curves of value. We need to revisit the digital view of the world to understand that it can be a source of error—particularly if we make the mistake of thinking only in analog terms.
Analog elements are typically not only analog (smoothly varying) but also linear: each small change in input produces a corresponding small change in output. For example, when we turn a volume knob up one notch, we expect that the relatively small change in the position of the knob corresponds to a relatively small change in the perceived loudness of the sound.
In contrast, digital elements are typically not only digital but also nonlinear: that is, knowing the size of the input change doesn’t give much ability to predict the size of the output change. Turning a system on is a kind of digital change. When we turn a power knob from “off” to “on,” the knob may only move as much as we moved the adjacent volume knob to make an almost-imperceptible change in the volume. But with the power knob, the relatively small change in the position of the knob gives no information whatsoever about how large the resulting change in loudness will be. Depending on how the volume was set and/or how the system is constructed, it might start up very quietly or very loudly.
Testing
For a linear analog system, it’s not hard to come up with a simple and sensible set of tests. There is some range of acceptable input: think of a volume knob, for example. We would want to check performance at the lowest acceptable input (knob turned all the way down); at the highest acceptable input (knob turned all the way up); and probably also at some middle input in the range between the two extremes. If the system performs acceptably on these three tests, and if the system is subsequently used for inputs only between the expected lowest setting and the expected highest setting, then the testers can have a high degree of confidence that the system will perform acceptably.
If the designers want to be conservative and cautious, they can build in a “safety factor” or “margin of error” by ensuring that their system performs acceptably for a range of input values much wider than the input values that are really expected to occur. This approach is essentially how modern society is able to build tall buildings or long bridges. We can rely on them because they are overbuilt for what we expect will happen to them.
Successful as that approach is in many important domains, it doesn’t work at all for programs, or in general for any system with many discrete states (such as computer hardware). To see why, consider this slightly ridiculous example of an infinite program that responds to numbers chosen by a user:
- Print “Pick a number”
- If the chosen number is exactly 27,873 then detonate a large pile of dynamite
- Otherwise print “OK” and go back to step 1
If you encounter a computer running this program and you don’t have a way of seeing these steps that make up the program, then it’s not obvious how you would learn about the particular value that detonates the dynamite. You could type a few different numbers at the program, but it would most likely look like a program that simply replies “OK” in response to any number at all. Even if you happened to try the immediately adjacent numbers 27,782 and 27,784, you’d get no indication that the number between them could have such an enormously different effect. This is nonlinearity with a vengeance!
It would be bad enough if these discrete nonlinear behaviors were the only source of trouble. They aren’t.
Massive Scale
Let’s assume that we have found a way to construct a process with smooth and linear behavior or that we have a tool that verifies the linear behavior of our process. Are we now in a position where it’s easy to write correct and predictable processes? Unfortunately, no. Now we have to be concerned about our second key problem: massive scale of state changes as a source of error.
What do we mean by massive scale? It’s not that any single change is itself a problem. It’s unusual for a problem with a computer program to be something conceptually deep and intellectually challenging, so that only a few brilliant people can understand the issue. (The problem of deep intellectual challenge is partly true for coordinating multiple processes, to which we will return later, but not for most kinds of programming.)
Instead, the typical problems with computer programs are roughly analogous to the problems of an architect designing a building. There are lots of small decisions to make and lots of rules as to how those decisions should be made for the best result. Any single problem in isolation is typically not very hard to solve. The challenge arises because there are a lot of decisions to be made, and sometimes they interact in unanticipated or unpleasant ways. “The breakfast nook should be about this big for comfortable seating … the mud room should be about this big … the back door should be here … oops, we’re close to the lot line now so let’s move the back door, oops, now the door swings into the breakfast table….”
So our problem in programming is not only the digital, nonlinear nature of the states we manipulate, as we previously mentioned. Those problems are even worse than they initially appeared, because of the sheer number of states that could be involved.
Modern computers are really fast—almost incomprehensibly so. When a computer’s specifications include a number with its “clock speed,” usually specified as some number of gigahertz (GHz), you can think of that as representing approximately how many additions the computer can accomplish every second: 1 GHz is a billion sums performed every second. That high speed is good because it means that computers can do really long sequences of steps to solve really hard or interesting problems, in ways that seem magical to a plodding human. But all that speed has a matching bad aspect: as we’ll see shortly, even relatively simple programs can have such large complex branching structures that they can’t be tested exhaustively. Of course, it’s not the speed itself that makes large untestable structures. Rather, increasing speed makes it feasible to build longer and more complex sequences as elements of our solutions. It is tempting to think that increasing speed of computation should be matched by increasing speed of testing, so that this issue wouldn’t really matter in the end; unfortunately, that casual optimistic analysis turns out to be incorrect.
Doubling
To give some context for the problem, a relevant story is about doubling on each square of a chessboard. In one version of the story, a fabulously wealthy emperor of old offered a reward to a cunning inventor (in some versions, the inventor of chess itself). The inventor asked “only” for one grain of gold on the first square, two grains on the second square, four grains on the third square, and continuing the doubling until the sixty-four squares of the chessboard were covered. The emperor felt very wealthy, wanted to reward the inventor, and was unfamiliar with how fast doubling grows. So he thought that the arrangement sounded OK, and agreed. As a result, he ended up handing over all his gold (and all his other possessions!) well before the board was covered.
To understand what happened in more detail, we can represent the number of grains of gold on each square using exponent notation. (You can just skip to the conclusion if you don’t like or don’t understand exponents.) The first square has 1 grain, which is 20, and the second square 2 grains, which is 21, the third square has 4 grains, which is 22, and so the nth square has 2n–1 grains of gold on it. As it happens, people who think about these things have estimated that all the gold ever mined in the world is less than 3 trillion grains. That’s a lot of gold, but 3 trillion converted into this exponent notation is less than 242. Accordingly, we can see that well before even the 43rd square of the 64-square chessboard, the unwise emperor would have run out of gold.
Branching
In the case of a program, the doubling to be concerned about is not the doubling of grains of gold but the doubling of test cases. If we have a simple program like this one:
If something is true then do thing 1; otherwise do thing 2
then we can see that we need at least two test cases: one where we “do thing 1” and the other where we “do thing 2.” Figure 6.1 represents this two-way choice.
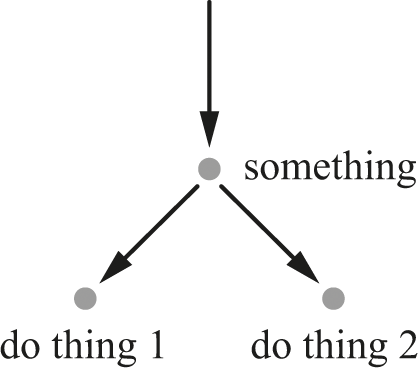
A two-way choice.
With the chessboard doubling, things got worse with each additional square to be covered. Our version of marching along to the next square of the chessboard comes if the program gets just a little bit more complicated. Let’s assume that “do thing 1” has more choices inside, like this:
If something-else is true then do thing 3; otherwise do thing 4
and “do thing 2” is similarly more complicated inside:
If yet-another-thing is true then do thing 5; otherwise do thing 6
Figure 6.2 captures this new branching.
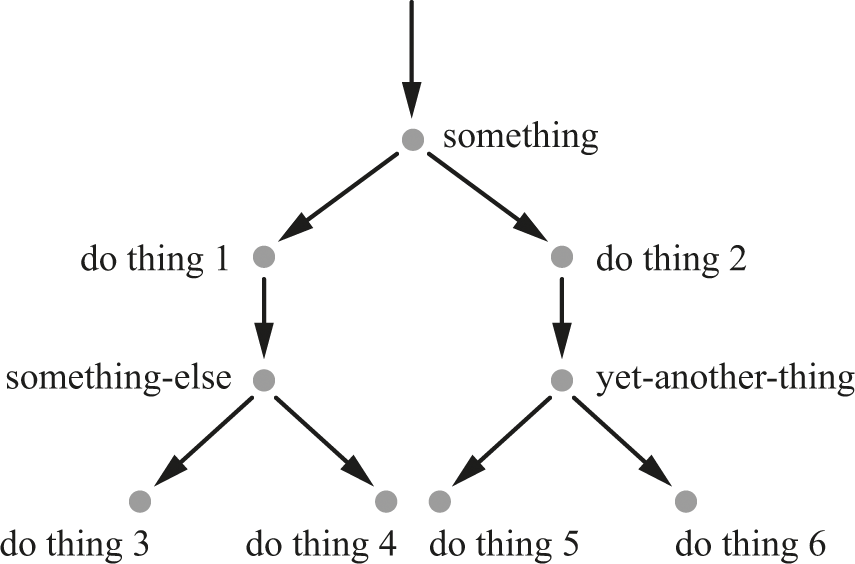
Multiple levels of choice.
We’ve been deliberately vague in this description. We’re just trying to capture the idea that each time we introduce another two-way choice we’re potentially doubling the number of test cases involved. The chessboard had only 64 squares, and that level of doubling was already enough to overwhelm the treasure of an empire. Now consider that the clock speed of a computer is also roughly the speed with which it can choose between possibilities—clearly when clock speed is measured in units of GHz (one billion actions per second) it doesn’t take long to build up an incomprehensibly large set of alternative paths.
Of course, no real program actually makes a new two-way choice at every single opportunity—it does some kind of “real work,” along with deciding which things to do. So a billion opportunities to make choices doesn’t necessarily mean a billion different choices. Even so, it’s easy to have a ridiculous number of alternatives.
What does the increase in possibilities mean in practical terms? It means that we have to abandon any idea of “complete coverage” or “exhaustive testing” for any but the very smallest and simplest programs. There are just too many possibilities. So if our programs contain errors, we have little confidence in our ability to find all of them.
But if we could find those errors, would we be in good shape? No. Surprisingly, the flexibility of software undercuts our efforts to build it well … as we’ll see next.
Malleability
In some ways, software seems like an ideal material. We don’t have to worry about its weight or its strength, and it doesn’t take heavy tools or enormous factories to produce it. If we can think clearly about a solution and write it down accurately, we don’t have a difficult fabrication process ahead of us—instead, we have basically produced the end product. Software offers very little resistance of its own and is easily shaped. Paradoxically, this very malleability of software is our third key source of trouble. Software exposes the weaknesses of our design skills and thinking.
Because it’s “easy” to write a line of program, it’s also “easy” to correct a line of program. That ease means that it becomes (apparently) less important to write any given line of software correctly. In fact, software professionals often want to make a program available to users as early as possible—typically, at the first point where it can be expected to be a net benefit for that user. At that early stage (which sometimes goes by a Greek letter like “alpha” or “beta”) the program likely still contains a huge number of known but unfixed errors. The expectation is that those errors will be found and fixed later.
This early-release behavior is economically rational in many cases, although it is unpleasant for an unsuspecting consumer. Often there is a premium on being first to market with the first viable implementation of some new product or feature; while you are the only available choice, you can rack up sales without competition from others. As long as your version is first to market and not too awful in its flaws, you will probably come out ahead of a competitor who is more careful but comes to market well after you.
Downloading fixes or new features has become widespread, even for products that were once sold as simple unchanging appliances. Embedded software in consumer electronics (such as a TV) used to be constructed with the expectation that it could not be updated once it left the factory. The software was built primarily around the expectation that it should work reliably without ever being updated, and accordingly it was not very sophisticated. However, modern consumer electronics are increasingly built with an expectation of internet connectivity and sophisticated software capabilities, with the corresponding increase of “software update” approaches to fixing or extending functionality.
Many people object to the practice of releasing poor software and fixing it later. There have been various attempts to solve this problem by essentially moralizing about it, shaming programmers in various ways, and/or pretending that the software is less malleable than it really is. But in almost all serious programming efforts, there comes some point at which a difficult choice must be made. At those times, the reality of software malleability almost always wins out over mere good intentions. In some unusual settings (like old-school consumer electronics, or NASA programming the space shuttle) there are real physical constraints on when and how software can be updated, and the malleability problem is accordingly less of a concern; instead, the concern is with ensuring that this essentially unfixable software is carefully built so that it doesn’t fail. But anywhere that the software is actually malleable, it is somewhere between rare and impossible for that malleability to be constrained and for people to focus on delivering programs that work the first time. Instead, customers are increasingly taught to be familiar with support websites, from which they can download “updates” that are improved versions of programs they already have. Or they use “cloud” services across networks, where the services available may be updated invisibly at any time. (We will look more at networks and clouds in chapters 13, 14, 18, and 19.)
Making Things Worse
Even worse is that the work done to fix detected errors sometimes introduces new errors. The underlying causes of flaws (human cognitive limits, misunderstandings, poor choices under pressure) don’t typically change between the first implementation and the correction or reimplementation. In some cases these problems actually get worse: “maintenance” work is low-prestige and so is often handed to less-capable programmers, even though the task of understanding and correcting someone else’s program is typically harder than writing a new program.
It’s glamorous to do something new, with the possibility that the result will be great. By comparison, it’s pretty unpleasant to deal with some old pile of junk and patch it yet again. Since programmers often aren’t very motivated to work on older programs, it’s common to see situations in which an attempt to fix a problem inadvertently creates a new problem, which might even be worse than the original problem. This phenomenon is a key reason why computing professionals are often distrustful of new versions of critical programs. Those same professionals often make elaborate arrangements that allow them to “roll back” to previous versions even after they install a new (and allegedly improved) version.
Some computer scientists have measured error rates in certain kinds of large programs. Those studies support the idea that there is actually a point at which it’s better to leave the program unfixed, because on average each “improvement” makes things worse. However, just as it’s hard to have the discipline to get programs right in the beginning, it’s very unusual to have the discipline to forgo “fixing” old programs. As with our other problems created by the apparently attractive malleability of software, it just seems so simple to go and fix the problem.
A closely related concern is the common misunderstanding of how expensive it really is to add a feature to a software product. Often it seems as though the work required to implement some small change is trivial—and the change, considered in isolation, might well be only a tiny effort. Unfortunately, it is very common for any such tiny change to have huge costs. The source of those costs may be only weakly related to the actual change required, but those costs are nevertheless unavoidable. One such cost is the integration of the new feature with the existing program—for example, a modified user interface to control the new feature’s behavior. Another such cost is the testing of the new feature, ensuring that it doesn’t break any of the program’s other features. There is no way to take short cuts on these costs. After all, if the feature isn’t made available to users, it isn’t actually useful. And because software is digital and nonlinear, involving enormous numbers of states, there really are no “small changes” that can bypass testing. Every programmer with extensive real-world experience has stories of how an apparently harmless change had severe unexpected effects.
Requirements
From earlier sections we know that the number of possible paths through a program can grow very rapidly as the program gets longer and has more decision or branching points. If there are any errors in our implementation, they may be hard to find. But if we put aside that concern with some kind of magical testing tool, are we OK? Unfortunately, no. We then run into the difficulty of accurately capturing requirements: our fourth and last key problem of this chapter.
Sometimes it’s hard to even decide what a system should do. For example, if the system is to be used by another person, we have to make some judgments about what that person will like or not like, what they will find helpful or annoying. Often we have trouble knowing our own minds, especially when dealing with complex trade-offs—but the problem is much harder when trying to establish someone else’s preferences.
Consider a program to sort numbers. At one level, it doesn’t seem very hard to say that the program should accept some numbers that might be out of order, and then provide the same numbers in sorted order. We might not have any idea how to do the sorting well, but surely it’s easy to explain what it means to sort numbers. But when we actually start trying to do the explaining carefully enough to build a program, we see there are challenges.
For example, how will the numbers be provided? (Typed in from a keyboard? Read from a file? Scanned from a document?)
Then we might ask, How will the result be delivered? (Displayed on a screen? Written into a file? Printed?)
Generally, when a program like this is written, it’s not running alone on the “bare metal” of the step-taking machinery. So there may be various kinds of services available to help tackle some of these questions for us, almost like magical spells we can invoke. Let’s assume that we can hand off many of these details so the program “only” needs to deal with the stream of input numbers and the stream of output numbers. Even so, there are still some design choices to be made where it’s partly a matter of judgment, rather than mathematically provable correctness.
Even when we have those supporting services to help us, there are questions that those services probably don’t know enough to solve. Are negative numbers OK, or are they a symptom of a misunderstanding? Are numbers with a fractional component or in scientific notation OK? Are words OK, and how should they be sorted in comparison to numbers if they are OK? Some of these comparisons can get quite bizarre, especially in terms of how they look on a page: for example, the zero-length (null) string “” compared to a single blank “ ” compared to two blanks “ ”—these are all different items, although we don’t usually find ourselves comparing them. It is possible to sort these, but is that really what we wanted?
Further, it’s not just user-to-program interactions that can be hard to design. There are challenges in taking a program that we’ve already constructed, and figuring out how to best have it interact with a new program that we’re building. For example, our number-sorting program may need to take numbers that are generated by some other measurement or analysis program. What is the format of the numbers generated by that program? How often does it generate them? How many numbers does it generate? How does the sorting program know that all of the numbers to be sorted have been received?
We’ve been getting a flavor of the challenges involved in fleshing out a vague problem statement into the requirements for a real working program. It’s even harder to take two programs written by other people, where these various trade-offs and detailed design choices may well be unknown, and figure out how to best combine them so they will work well together. And yet that is the kind of task that faces real-world system builders all the time.
Expressing Requirements
Separately from the serious problem of how to figure out what the requirements are, there is a serious problem of how to express the requirements so that they can be understood. Even if you believe you know something about how a complex system will work, that’s not the same as expressing it so that another person will have the same understanding.
For example, you might have a high degree of confidence that you, personally, would be able to separate numbers from non-numbers and sort the numbers—but that doesn’t necessarily mean that you have the same degree of confidence that you could write down all the tests and cases for someone else to behave in the exact same way. As we solve problems, it is easy for us to rely on tacit knowledge: knowledge that we may use without being aware of it and without necessarily knowing how to articulate it.
If you are an adult reader of this book, there’s a fairly good chance that you know how to ride a bicycle. But your ability to ride a bicycle doesn’t mean that you can write a book that would allow someone with no previous experience to ride a bicycle well.
A further, closely related question is whether you can express some procedure so that a computer or mechanical implementation (rather than a person) can match your understanding. To return to riding a bicycle, we can see again that being able to ride a bicycle does not imply an ability to write a program so that a robot could ride a bike.
Specifications
Even if we have some good way of expressing requirements so that we can distinguish between success and failure in solving the problem, we may still struggle with expressing specifications. The specifications express some preferred set of solutions that meet the requirements. Compared to the requirements, they are closer to the ultimate implementation technology while still preserving some implementation flexibility.
Most statements of requirements and specifications are written informally in human (natural) languages. Those descriptions have the advantage that they are comfortable for the reader, but they are hard to write precisely—natural languages seem to all come with a considerable degree of ambiguity and fuzziness in their typical usage. As a result, it’s hard to write natural-language text that is sure to be understood exactly the same way by different readers. For an informal confirmation of this problem in a different domain, we can look at court cases. Although some legal disputes turn on different versions of facts and the evidence supporting those contested versions, there are also a surprising number of cases where the facts are not in dispute but the correct application of the law is in doubt. Even when regulatory agencies attempt to produce very detailed rules, there are often disputes about what terms mean or how they apply in particular situations.
In contrast, formal (artificial) languages can be much more precise and can be used to produce specifications that represent the same functionality when analyzed by different readers. By developing exact grammars and rules, and using formal semantics, we can be very precise about the meaning of a statement like
P → A | B | C • D
(This equation doesn’t necessarily mean anything interesting. It’s just an example of how these kinds of statements look in various formal languages.)
However, any such formal language requires specialized knowledge, making it unlikely that “real users” will be able to genuinely understand and review the description for accuracy.
There seems to be an awkward but unavoidable trade-off. On one hand, there are languages that are imprecise but can be reviewed for accuracy. On the other hand, there are languages that are precise but cannot be reviewed for accuracy. To date, the best compromise between precision and accuracy probably occurs when formal specifications are produced and then converted into natural language by people who are competent in both the formal language and good (natural language) writing. However, such a process is expensive and inevitably introduces additional opportunities for error, since there are additional translation steps required.
Mock-ups
Building a mock-up (a limited implementation) is another common approach to capturing requirements and specifications. Building a “quick and dirty” version of a sorting program, for example, would force us to identify issues about the boundaries of the acceptable inputs—so we would then be better prepared to ask the right questions of the users. In addition, having the users try out our sorting program might well prompt them to notice things we hadn’t done right (or to confirm the things we had done right).
Such an approach is often particularly useful for certain domains where a language-based description is hard to understand: for example, when trying to design how a website looks and how users will interact with it. However, the approach is not a universal solution. Mock-ups by their nature leave out details. Ideally, those details don’t matter. But it is sometimes hard to be sure what matters and what doesn’t.
One response to these problems has been to build programming practices around repeated iterations of small changes to the product or service. This approach sidesteps some of the problems of requirements and specifications in favor of a belief that repeated tinkering eventually leads to recognizable improvements. The lurking hazard is that there may never be a point at which anyone is thinking about the whole system in any kind of architectural or strategic way. If we start with a small car for a job that really needs a semi-trailer truck, it won’t matter how many after-market accessories we add or how many times we repaint the exterior—the car will still be inadequate for the job. Sometimes there is a similar challenge when people think entirely in terms of small increments of functionality, even though the approach is appealing for limiting the scope and risk of any given change.
Implementation
Now we know that there are problems with capturing and specifying what systems should do. Let’s put those problems aside for a moment. Repeating a common pattern in this chapter, there are still problems lurking: even if we assume a perfect specification, there is still the problem of ensuring that the implementation matches the specification.
A specification is the “higher level” description of what we want to happen. Correspondingly, an implementation is the “lower level” realization of how we want it to happen. A correct implementation is one that exactly meets its specification. Given a complete, precise, accurate specification, building a correct implementation is much easier; many programming errors arise from problems of specification incompleteness or inaccuracy, not from programmers being unable to write correct programs. Nevertheless, it is also true that having a good specification is not always sufficient to write a flawless program; errors can also arise from misunderstandings or the incompetence of programmers.
It’s very unusual for a programmer to build something that doesn’t work at all, in at least some important cases. But it’s very common, bordering on universal, for a programmer to neglect at least some minor, obscure, or unusual cases—or to get a boundary condition “off by one.”
This clustering of problems along boundaries is one reason that testing a program can be useful, in spite of the explosion of possible paths we mentioned previously. Although the program’s execution may proceed along many different paths, programmer errors will tend to cluster along only a few of those paths. We may recall our example (earlier in this chapter) of the program that exploded on a particular single input value. Although it is possible in principle for a program to have such a completely arbitrary behavior, in practice that situation is unusual. Instead, human problems of poor communication and/or cognitive limits tend to produce particular kinds of implementation errors, which can often be prevented, or found and removed.
From the use of discrete states to the challenges of implementation, we’ve now identified some of the most important ways in which programs are usually flawed. We’ll next take up some of the ways programs are limited even when they are flawless.