Igen kevés ember van, aki a legapróbb részletekig érti Einstein általános relativitáselméleti egyenleteit. Ezek egyike Steven Weinberg, a Nobel-díjas fizikus, nagy hatású monográfiájában, amelynek címe A kozmológiai állandó problémája, ezt írta: „Sajnos nem volt elég egyszerűen elhagyni a kozmológiai állandót, mert bármi, ami a vákuum energiasűrűségéhez hozzájárul, éppen úgy viselkedik, mint egy kozmológiai állandó.”52 Einstein a kozmológiai állandó bevezetésével egy új matematikai eszközt hozott létre a tudomány számára - amelyet még ő sem tudott később visszavenni. Csak az maradt kérdéses, hogy az új találmányt a fizikusok és a kozmológusok fel tudják-e használni a világegyetemről alkotott elméletekhez.
Ha a kozmológiai állandó pozitív, akkor egy taszítóerő száll szembe a tömegvonzással. Einstein az állandót azért vezette be, hogy valami megtartsa az egyenletei szerint befelé összeomlani készülő világegyetemet. Tulajdonképpen mesterségesen létrehozott egy erőt, amely nem engedi összehúzódni a világegyetemet. Így tehát, amikor kiderült, hogy a
világegyetem tágul, Einstein kivette az egyenletből a kozmológiai állandót.
Amikor Alexander Friedmann szakított Einstein feltételezésével, hogy a világegyetem statikus, és Einstein eredeti téregyenletének megoldásául egy táguló világegyetemet kapott, új fejezetet nyitott a modern kozmológia történetében. Itt volt az ideje, hogy Lemaitre és mások feltegyék a magától értetődő kérdést: Ha a világegyetem tágul, ez a folyamat mikor kezdődött? Az ösztönös válasz erre az lenne, hogy valamikor a távoli múltban a világegyetem nagyon-nagyon kicsi, forró és sűrű volt. Ebből a kicsi és sűrű anyag- és energiacsomóból egy gyors változással keletkezett a világegyetem. Fred Hoyle, egy cambridge-i kozmológus az 1940-es végén egy rádióelőadásban „Big Bang”-nek, ősrobbanásnak nevezte el ezt a hihetetlen erejű hirtelen kiterjedést, amely elindította világegyetemünket a tágulás útján.
A téridő görbülete az adott objektum tömegével arányosan nő, ezért, amikor a világegyetem még nagyon kicsi volt, a tér görbülete óriási lehetett. Amikor az egész világegyetem még csak egy pont volt, az idő sem telt, mivel ebben a pontban - a téridő szingularitásában - a tömegsűrűség végtelen, és a tér és az idő elméletei nem alkalmazhatóak. Az idő fogalma a szingularitási pontban nem értelmezhető. Lemaitre a világegyetem kezdőpontját ezért egy „tegnap nélküli napnak” nevezte.
Az oxfordi egyetemen dolgozó Roger Penrose 1965-ben megjelentetett egy cikket, amelyben topológiai fogalmakkal írja le, hogy egy nagy tömegű objektum hogyan tud egy pontra összezsugorodni - összeomlani saját súlya alatt. Ennek eredménye mindig egy fekete lyuk lesz; ezt a folyamatot először Karl Schwarzschild úttörő munkájából ismerhette meg a világ, aki Einstein téregyenletének első megoldója volt, és aki bevezette a ma Schwarzschild-sugár néven ismert fogalmat. Ez az a méret, amelynél ha kisebb egy csillag valódi sugara (ezt a
csillag tömege határozza meg), akkor a csillag egy ponttá zsugorodik. A Schwarzschild-sugár a kritikus pont - minden objektum, vagy fénysugár, amely egy olyan fekete lyukba kerül, amely ez alá az érték alá esik, örökre elvész. Penrose bebizonyította, hogy a fekete lyuk közepén van egy különleges pont. Ez a pont a téridő szingularitás. Itt végtelen a görbület, és az idő megszűnik.
Penrose ragyogó meglátásának az a következménye, hogy egy csillag tömegösszeomlása során el kell, hogy jusson egy olyan állapotra, amelyből nincs kiút. Matematikai nyelven ezt úgy lehet mondani, hogy a csillag belsejében egy zárt felület keletkezik, és amint egyre gyorsul a visszafordíthatatlan összeomlás, az eredmény a szingularitás lesz: az a pont, ahol az általunk ismert matematika és fizika nem alkalmazható. Még ha a csillag nem tökéletesen gömb alakú, akkor is összeomlik, és szingularitás követezik be.53 Egyébként az idő már sokkal a szingularitás előtt, a Schwarzschild-sugár elérésekor megáll - a külső szemlélő ezt látja. Így ha valaki egy fekete lyukba esne, a külső szemlélő azt látná, hogy az illető megfagy a Schwarzschild-sugár által meghatározott gömb felületén. A szegény áldozat pedig nem is tudna magáról.54
Az a gond a szingularitással, hogy az általunk ismert matematikai és fizikai fogalmakkal nem igazán írható le. Matematikai értelemben az a szingularitás, amikor valami „kóros” dolog történik. Egy egyszerű példával megérthetjük. Ha az y = fx) egyváltozós függvényre gondolunk, ez lehet egy „jólfésült” függvény: sima és folytonos, differenciálható (tehát meg lehet állapítani a függvény minden egyes pontján a

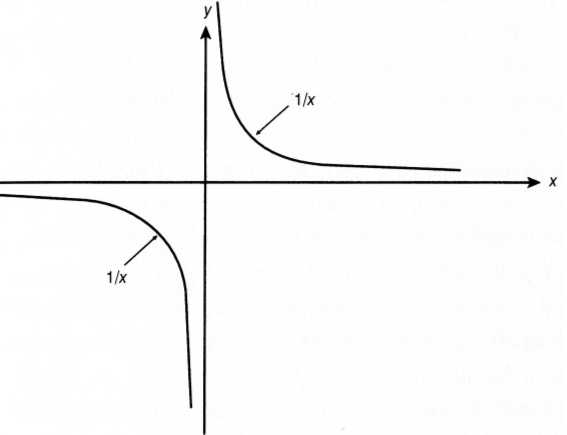
Egy fekete lyuk közepében (a világegyetem kezdőpontjában) minden törvény érvényét veszti, ugyanúgy, ahogyan az y = 1/x függvény nem értelmezhető az x = 0 helyen. A gravitáció végtelen, a téridő görbülete végtelen, az idő megáll.
Penrose fordítva érvelt - ez nem ütközik az általános relativitáselmélet törvényeibe - az összeomlástól a tágulás felé. Így, ha a „filmet” visszapörgetnénk az összeomlás pillanatától, akkor azt látnánk, hogy a világegyetem egy fehér lyukból származik - egy téridő szingularitásból. Mivel ezen a ponton a matematika és a fizika nem működik, és nem tudjuk, mi történik a robbanás előtt, ha feltételezzük, hogy akkor keletkezett a tér és az idő, a világegyetem kezdetéről szóló elméletek általában az ősrobbanás utáni másodperc első kis töredéke eltelte után kezdődnek. Itt lényegében két megközelítést ismerünk.
A szokványosabb ősrobbanási elmélet azt állítja, hogy a hatalmas robbanás után a tér tágulni kezdett. Egy kicsit később létrejött a barionanyag; ez az általunk ismert anyag őse, protonok, elektronok, neutronok, mind egy nagyon forró őslevesben, amely a tágulás során lassan hűlni kezdett. Ez a korai világegyetem a nagy sűrűség miatt nem volt átlátszó, hiszen a fotonsugárzás elnyelődött, majd újra kibocsátódott. A világegyetem csak körülbelül 300 000 éves korára lett elég átlátszó ahhoz, hogy a fotonok egyenes vonalban haladhassanak. A korai világegyetemet behatárolta átlátszatlansága.
Ha az egyre erősebb távcsövekkel egyre távolabb tekintünk az űrbe, ezzel időben is egyre hátrébb látunk, amíg el nem érünk egy határt. Ha távcsöveinkkel 14 milliárd fényévnyire látnánk, akkor semmit nem látnánk. A legtöbb becslés a világegyetem korát 12 és 14 milliárd év közé teszi, így a 14 milliárd évvel ezelőtti időpont valamikor az ősrobbanás körül 300 000 éves környezetében lehet. De 300 000 éves korában a világegyetem még átlátszatlan volt, ezért ilyen távolságban, vagy ennél messzebb semmit sem látnánk.
Az ősrobbanás után kb. egymilliárd évvel megjelentek az első csillagok és galaxisok. Utána kialakultak a galaxishalmazok és szuperhalmazok. A világegyetem tovább tágult, míg végül elérte mai méretét.
A felfúvódó (inflációs) világegyetem elmélete másképpen magyarázza a világegyetem fejlődését, mint a szokásos ősrobbanás-elmélet. Alan Guth fizikus, az MIT Weisskopf fizikusprofesszora 1979-ben megalkotta a felfúvódó világegyetem modelljét. Alan Guth a New Jersey-beli New Brunswickben született 1947-ben. Az MIT-n szerzett diplomát 1969-ben, majd ott szerzett fizikai doktori címet is 1972-ben.
Princetonban fizikát oktatott, a Columbia Egyetemen pedig kutatásokat végzett, majd részecskefizikával foglalkozott a Cornell Egyetemen. 1979 őszén egy évre elhagyta állását a Cornellen, hogy a Stanfordi Lineáris Gyorsító Központban dolgozzon. Decemberben ragyogó ötlete támadt. Guth is azt próbálta elképzelni, hogy mi történhetett az ősrobbanás utáni pillanatokban, és elméletével a kozmológia két nagy rejtélyét is megoldja: a laposság- és a horizontproblémát.
A laposságprobléma akkor merül fel, ha valaki azt hiedelmet támogatja a világegyetemmel kapcsolatban, hogy a világegyetem geometriája lapos (sík), vagy euklideszi. Guth és kozmológus elődei ezt a következtetést a világegyetem anyaga sűrűségével kapcsolatos becsléseikből vonták le. Kiszámították a világegyetem kritikus sűrűségét: azt a sűrűséget, amelyen a világegyetem sem nem omlik össze, sem nem tágulna tovább állandó vagy gyorsuló sebességgel, hanem a tágulás egyre lassulna, majd végül megállna. A tudósok szerint a világegyetem jelenlegi sűrűsége e kritikus érték közelében van (a „közelében” itt a kritikus sűrűség egy tört részét, vagy akár a kétszeresét is jelentheti). Úgy jutottak erre az eredményre, hogy a becsléseiket arra az időre extrapolálták, amikor a világegyetem még nagyon fiatal volt. Véleményük szerint egy másodperccel az ősrobbanás után a világegyetem sűrűsége a kritikus sűrűséggel 15 tizedesjegyig megegyezett. Akkor viszont a világegyetem hihetetlenül lapos. De miért? A szokásos ősrobbanáselmélet erre nem ad választ.
A szokásos ősrobbanás-elmélet másik nagy problémája a horizontprobléma. A horizont, csakúgy, mint a Földön, az a pont, amelynél távolabbra nem látunk. Relativitáselméleti kontextusban, ha egy fényjelet messzebbről küldenek nekünk, mint ahonnan az meg tud érkezni, akkor azt a horizonton túlról küldték.
A Hawaii Egyetemen dolgozó Esther Hu és munkatársai 1998-ban arról számoltak be, hogy a világ legnagyobb távcsövével, a 9,8 méteres Keck-ikertávcsövek egyikével megpillantottak egy eddig túl távolinak bizonyuló galaxist. Ez a halvány galaxis mintegy 13 milliárd fényév távolságra van tőlünk. A világegyetem körülbelül 14 milliárd éves. Tételezzük fel, hogy Hu, vagy egy másik csillagász az égbolton az ellenkező irányba nézne, és megpillantana egy másik, tőlünk szintén 13 milliárd fényév távolságra lévő galaxist. Ez a két galaxis nyilvánvalóan kívül esik egymás horizontján. Miért? Mert a világegyetem csak 14 milliárd éves, és a fény az egyikből a másikba 13 + 13 = 26 milliárd év alatt jutna el, ami ennek az időnek majdnem a kétszerese.55 A fény tehát nem érkezik meg egyik galaxisból a másikba. Továbbá, a világegyetem tágulása miatt a két galaxis a fénysebességgel összemérhető sebességgel távolodik egymástól, és a fény ezért soha nem jutna el az egyik galaxisból a másikba.
A horizontproblémát a kozmikus háttérsugárzás tanulmányozása vetette fel. Hogyan lehet ez a sugárzás ennyire homogén (1 a 100 000-hez), ha minden egyes irányból érkezik? Mivel a különböző irányban elhelyezkedő pontok nem „látják” egymást, amikor egymás horizontján kívül kerülnek, nem állhat fenn közöttük olyan információcsere, amelynek az eredménye homogenitás lehetne.
Ezen jelenségek magyarázatára alkotta meg Guth a felfúvódás-elméletet, amely azt mondja ki, hogy az első másodperc első töredékében a világegyetem hatalmas, exponenciális mértékben tágult. Guth kozmológiája egy, a részecskefizikusok által jól ismert mechanizmust idéz fel, amely megmagyarázhatja, hogy a korai világegyetemben egy különleges anyagforma olyan gravitációs taszítást hozhatott létre, amely a világegyetem tágulásának hajtóerejét jelentheti. Ez a tágulás tartja meg a tér homogenitását, és teszi lehetővé a horizontprobléma végső megoldását. Ugyanakkor az ezen erő által előidézett tágulás hatására a világegyetem el fogja érni a kritikus sűrűséget.
A felfúvódásnak több különböző formája is van. Az einsteini egyenlet kozmológiai állandója a felfúvódás-elméletet hihetőbbé tenné. Az is lehet, hogy a legújabb, a világegyetem gyorsuló tágulását alátámasztó eredmények megtárgyalására összegyűlt kozmológusokat az vezette vissza a kozmológiai állandóhoz, hogy szerették volna megtartani a lapossági feltételezést, és ezzel együtt a felfúvódáselméletet.
Alan Guthban először akkor merült fel a felfúvódó világegyetem gondolata, amikor a mágneses egypólusokat (monopólusokat) vizsgálta. E részecskéknek a szokásos mágnes két pólusával szemben csak egy pólusuk van. Némely elméletek szerint ilyeneknek létezniük kellene a világegyetemben - mégsem léteznek. Munkája a Higgs-mező elméletén alapult, amely elméleti eszközt gyakran használják a részecskefizikában. A Higgs-mezőt a gyakorlatban még nem észlelték, de némely tudós szerint ezzel magyarázhatók a természetben a nem tökéletes szimmetriák. Guth felfúvódó világegyetem-elmélete szerint világegyetemünk egy nagyobb, szuper-világegyetem része, és az ott jelenlévő vákuumingadozás eredményeképpen jött létre. Guth elmélete szerint elképzelhetőek más „gyermek-világegyetemek” is, amelyek szintén az anya-világegyetemtől származnak. Még az is lehetséges, hogy egy szuperfejlett civilizáció laboratóriumi úton is létrehozhat ilyen gyermek-világegyetemeket.
Hogyan győződhetünk meg arról, hogy az ősrobbanás valóban megtörtént? Ha a galaxisok távolodnak egymástól, akkor régebben közelebb voltak. Ha ezt az elvet visszavezetjük az időben, akkor arra a következtetésre jutunk, hogy a kezdő időpontban minden együtt volt. De honnan tudjuk, hogy valóban így volt-e? Ha a világegyetem egy ősrobbanással kezdődött, és közvetlenül ezután elkezdte a kiterjedést, egészen a mai napig, akkor kezdetben nagyon forró volt, és azóta folyamatosan hűl. George Gamow, Ralph Alpher és Robert Herman elméleti fizikusok az 1950-es években azt állították, hogy az ősrobbanásról árulkodó sugárzások még fellelhetők a világegyetemben. Vagyis, ha a világegyetem az ősrobbanáskori hihetetlenül magas hőmérsékletről folyamatosan hűl, akkor mostanra el kellett érnie egy mérhető hőmérsékletet.
A princetoni Robert H. Dicke és James E. Peebles az 1960-as években hasonlóan gondolkodtak, és ki is számították a fent említett sugárzás, az ősrobbanás okozta feketetest-sugárzás mértékét. A feketetest-sugárzást minden test kibocsátja az abszolút 0 fok hőmérséklet fölött. Ez a sugárzás észlelhető. A legjobb példa erre a meleg testek által kibocsátott infravörös sugárzás. De még a hidegebb testek is sugároznak, alacsonyabb energiaszinteken.
Amikor a fotonok kiszabadultak az őslevesből, és a világegyetem az ősrobbanás után mintegy 300 000 évvel elkezdett átlátszóvá válni, a fotonok egyenes pályákon kezdtek közlekedni, és ezt a tulajdonságukat máig megtartották. A Doppler-hatás miatt ezek a fotonok energiát vesztettek. Jelenlegi energiaszintjüket - és így hullámhosszukat is - ki lehet számítani az elméletből.
1965-ben a Bell Laboratóriumok két rádiócsillagásza éppen ezt fedezte fel, anélkül, hogy ismerték volna az elméletet. Arno Penzias és Robert Wilson később Nobel-díjat is kaptak a mikrohullámú háttérsugárzás felfedezéséért. 1989-ben a NASA fellőtte a COBE (Cosmic Background Explorer, vagyis kozmikus háttérsugárzás-vizsgáló) műholdat, amelynek segítségével még pontosabb méréseket lehet végezni. A világűr bármely irányából meglepően hasonló sugárzási értékeket mértek; ez az érték 2,7 fokkal magasabb az abszolút 0-nál (2,7 °K). Ez a felfedezés a Hubble-törvénnyel együtt az egyik legfontosabb csillagászati tény, amely alátámasztja az ősrobbanás elméletét. A sugárzás egyenletessége valószínűleg a felfúvódó világegyetem elméletét támogatja. A csillagok, galaxisok és galaxishalmazok feltehetően az ősrobbanáskor és a korai világegyetemben bekövetkezett energiaegyenetlenségek következtében jöttek létre.
Az ősrobbanás-elmélet egy másik bizonyítéka a világegyetem kémiai elemeinek viszonylagos bősége. A tudósok kiszámították az elemek várható túlsúlyát az ősrobbanás-elmélet szerint. Az ekkor felszabadult energia szintje alapján a világegyetemben kb. 75% hidrogénnek és 25% héliumnak kellene lennie. Az összes többi elem (és a deutérium, a hélium-3 és lítium-7 izotópok) csak nyomokban lennének jelen a világegyetem összetevői között. Ezek a nehezebb elemek - amelyek a körülöttünk lévő világ, sőt a mi saját összetevőink (bár a hidrogén is testünk egyik fő eleme) -később jöttek létre, a csillagokban bekövetkezett nukleáris reakciók során. A világegyetem elemei keletkezésének tanulmányozása megerősítette ezt a feltevést. Ezek a kutatások tehát az ősrobbanás-elmélet bizonyítékának tekinthetők.
Az ősrobbanással kezdődött a világegyetem tágulása. Függetlenül attól, hogy ez a tágulás exponenciálisan kezdődött-e, ahogyan azt a felfúvódáselmélet állítja, vagy sem, a kérdés a következő: Milyen a kozmikus tágulás? Erre a legjobb analógiát az Eredetek: A modern kozmológusok élete és világa című könyvben találtam.56 Vegyünk egy gumidarabot, és jelöljünk meg rajta mondjuk centiméterenként egy-egy pontot tollal. A tintapöttyök jelentsenek egy-egy galaxist. Most húzzuk szét a gumidarabot. Vegyük észre, hogy eközben a pontok távolodnak egymástól. A galaxisok közötti távolság tehát nő; 1 cm-nél nagyobb lesz. De mi történik két nem szomszédos ponttal? Ezek még gyorsabban távolodnak: a köztük lévő távolság gyorsabban nő. Ha a gumidarabot úgy húzzuk ki, hogy a pontok/galaxisok közötti távolság 2 cm legyen, akkor két másodszomszéd-galaxis most 4 cm-re lesz egymástól. Ez történik a kozmikus tágulás során is.
Amikor a tér tágul, a viszonylag közeli galaxisok lassabban távolodnak egymástól, mint a távolabbiaktól. Két galaxis között a távolodás sebessége távolságukkal arányos. Ez pedig éppen a Hubble-törvény.
Vegyünk észre egy másik fontos tulajdonságot is. A gumidarab kihúzásakor minden pont ugyanúgy távolodik szomszédaitól. Nincsen kiváltságos pont: mindegyik tekinthető a tágulás középpontjának, amelytől az összes többi pont távolodik. A világegyetemnek sincsen középpontja és széle. Még ha azt is látjuk, hogy minden galaxis távolodik tőlünk, tudnunk kell, hogy ez bármelyik galaxisból így látszik -mindenki úgy érezheti, hogy a tágulás középpontjában áll.
Mi okozza a kiterjedést? Tér jön létre, vagy nyúlik meg. Az általános relativitáselméletből tudjuk, hogy a tér képlékeny; egy olyan alakítható közeg, amelynek a geometriáját megváltoztathatják a gravitációs hatások. A világűr nem olyan üres, mint amilyennek látszik. A világűr egy éppen sülő kuglófként tágul. Az Esther Hu és társai által felfedezett galaxis a fény sebességének 95,6%-ával távolodik tőlünk. Ez történik -legalábbis a Földről nézve - az innen látható legtávolabbi galaxisokkal. A hétmilliárd fényévnyire lévők a fénysebességnek körülbelül a felével távolodnak. Ha még közelebbi galaxisokat vizsgálunk, a tőlünk való távolodás sebessége kisebb.
Legjobban akkor érthetjük meg ezt a furcsa, nehezen hihető jelenséget, ha feltételezzük, hogy a világegyetem végtelen. Ha így van, akkor bármely pontja tekinthető középpontnak, és az itt lévő megfigyelő azt látná, hogy a közelebbi galaxisok lassabban, a távolabbiak gyorsabban távolodnak tőle, a távolságukkal arányos sebességgel. Egy kozmikus mazsolás kuglóf esetében minden mazsolaszem azt látná, hogy a többi mazsola a távolságával arányos sebességgel távolodik tőle. Ilyen egyenletes tágulás folyik az üres világűr közegében.
A távoli szupernóvákkal kapcsolatos új megfigyelések arra utalnak, hogy a tér nemcsak tágul, hanem gyorsulva tágul. Valami kifelé nyomja. Mi lehet ez az erő? A kvantumfizika szerint az űr, a vákuum - egyáltalán nem vákuum, hanem tele van energiával. Virtuális részecskék jelennek meg és tűnnek el az „űrben”. Rengeteg energia van odakint, amely úgy látszik, mintha üresség lenne; nem ismerjük ezt az energiát, és nem tudjuk, honnan jön. Olyan a vákuum, mint egy összenyomott rugó, amely ki akar tágulni. A láthatatlan rugó által gyakorolt nyomás miatt tágul a tér. De a rugó sokkal lassabban tágul, mint a tér, amelyet tágít, a tágulás tehát gyorsul. A vákuumenergia, a teret kifelé nyomó erő modellje: Einstein kozmológiai állandója.57
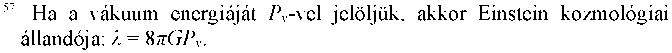
A világegyetem természetének tanulmányozása során az érdekli leginkább a tudósokat, hogy milyen az anyag összetétele. Mi az anyag? A világegyetemnek ez a fő összetevője, vagy másféle elemek is szerepet játszanak a világegyetem tulajdonságainak kialakulása során? Az általános relativitáselmélet felől, vizsgálva a kérdést, az anyag milyensége határozza meg Einstein T energia-impulzus tenzorát. Az anyag különbözőképpen viselkedik a huszadik század két fontos fizikai rendszerében: az általános relativitáselmélet, illetve a kvantumelmélet keretei között. Az általános relativitáselmélet az anyag (és a tér és az idő) „nagy léptékű” tulajdonságait határozza meg, míg a kvantumelmélet a „kis léptékűeket”. Az első egy teljesen determinisztikus elmélet, míg a második természete probabilisztikus: a kvantumok birodalmában a kérdésekre adott válaszok nem pontos számok, hanem valószínűségeloszlások. A kvantumelmélet, egyéb eredményei mellett, vezetett a korábban nem ismert anyagrészecskék felfedezéséhez.
Amikor a huszadik század elején felfedezték a kvantumelméletet, a fizikusok csak a neutronokat, protonokat és elektronokat ismerték. Utána felfedeztek egy érdekes fajtájú radioaktív bomlást, amelynek során a neutron egy elektront és egy protont bocsát ki. Wolfgang Pauli 1930-ban megvizsgálta a rendszer reakció előtti és utáni energiaállapotát, és ennek alapján azt feltételezte, hogy a reakció során egy eddig ismeretlen részecskének is fel kell szabadulnia. Egy évre rá az Amerikában élő, olasz származású Enrico Fermi a kilőtt részecskét neutrínónak (kis neutronnak) nevezte el. Úgy gondolták, hogy ez a részecske felelős a radioaktív bomlás után hiányzó energiáért.
A neutrínót töltés nélküli részecskeként ismerték meg, és 1998 júniusáig úgy gondolták, hogy tömege sincsen. Legalábbis soha senki nem mért neutrínótömeget. Fred Reines és Clyde Cowan 1956-ban felfedezte, hogy a Savannah folyó melletti nukleáris reaktor neutrínókat bocsát ki. Cowan 1995-ös halála után Reines Nobel-díjat kapott annak a részecskének a felfedezéséért, amelynek létezését elméletileg már negyedszázaddal korábban bizonyították. Valóban megtalálták tehát azt a részecskét, amelyet tulajdonképpen tudósok gondoltak ki, mert valami hiányzott a nukleáris reakciók végtermékeiből! A neutrínó története jó példa arra, hogy az elmélet és a matematika valóban alkalmas a tudás előmozdítására, és hogy ha egy jó elméleti tudós bízik saját feltevéseiben, az kísérleti sikereket is hozhat. De a neutrínó történetének ez csak a kezdete volt.
Amikor a tudósok kezdték alaposabban megismerni a magfúzió működését, biztosak voltak benne, hogy egy ilyen nukleáris reakcióból származik a csillagok energiája is. És ha a csillagok belsejében égő tűz valójában egy nukleáris fúzió, amely fantasztikus energiamennyiségeket szabadít fel, akkor a csillagok - a mi Napunkkal együtt - bizonyára neutrínókat bocsátanak ki. A tudósok úgy képzelték, hogy a Földre folyamatosan érkeznek a töltés nélküli, elhanyagolható tömegű részecskék, de elképzelhetetlenül kis méretük miatt úgy hatolnak át a Földön, mintha az ott sem lenne. Hogyan tudnák a tudósok észlelni ezeket a Napból jövő részecskéket?
Csak úgy volt esély a világűrből érkező neutrínók észlelésére, ha hatalmas, mélyen fekvő (például bányákban -azért kerültek a föld alá, mert itt jobban meg voltak védve a másféle sugárzástól) medencékben különböző fajtájú folyadékokat helyeztek el, és ott próbálták megfigyelni a neutrínók és a vízmolekulák (illetve egyéb molekulák) közötti kölcsönhatásokat. A Föld több pontján is folytattak ilyen kísérleteket. Az első olyan neutrínókat, amelyek a Földön kívüli forrásból származtak, egy dél-afrikai aranybányában, 1965-ben fedezte fel Fred Reines kollégáival együtt. Időközben találtak egy másféle neutrínót is, amelynek a neve müon-neutrínó, és a Brookhaven Nemzeti Laboratórium nukleáris reakcióinak melléktermékeként észlelték. A Stanfordi Lineáris Gyorsító Központban pedig felfedezték a tau részecskét, amelynek jelenlétéből egy harmadik típusú neutrínó létezésére következtettek. Sóbányák medencéiben is folytattak neutrínókereső kísérleteket, és ezek sikerrel is jártak, eltekintve attól, hogy az elméletileg jósoltnál sokkal kevesebb neutrínót találtak, és nem értették, hogy miért.
Később kiderült, hogy az elmélet itt is megelőzte a kísérleti eredményeket. Az 1950-es évek vége felé egyre több fizikai elmélet született arról, hogy a neutrínók egy elképesztő tulajdonsággal rendelkeznek: képesek alakjukat megváltoztatni. A fizikusok ezt a jelenséget neutrínóoszcillációnak nevezik. Így egy elektron-neutrínó müon-neutrínóvá vagy tau-neutrínóvá változhat (mindhárom név a nehezebbik részecskétől, tehát az elektrontól, a müontól illetve a tauontól származik). Ezek egyike könnyen észlelhető, de a többi nem. Így a tudósok arra a következtetésre jutottak, hogy a Napból jövő neutrínók némelyike esetleg azért nem észlelhető, mert időközben megváltozik a típusa.
Az 1980-as évek végén hatalmas észlelőmedencék készültek az Egyesült Államokban (az Irvine-Michigan-Brookhaven kísérletet egy ohiói bányában folytatták le) és Japánban (a Kamioka Neutrínómegfigyelőben, a „japán Alpok” egyik cinkbányájában, Takayamától 45 km-re északra). Az utóbbi egy föld alatti, 47 000 m3-es vízgyűjtő medence volt, tele különlegesen tiszta vízzel, és körülvéve nagy érzékenységű fényérzékelőkkel, amelyek a kutatók reményei szerint érzékelni fogják azokat az egyszeri fényjeleket, amelyek a neutrínók és a vízmolekulák egy atomjának ütközéséből származnak. 1987-ben a déli féltekéről megfigyelhető volt egy szupernóva robbanás a Nagy Magellán-Felhőben; mindkét hatalmas neutrínóérzékelő kísérlet során találtak innen származó neutrínókat. A neutrínóknak tehát át kellett hatolniuk a Földön ahhoz, hogy az érzékelőkbe jussanak. Ezek voltak az első, bizonyítottan a Naprendszeren kívülről származó neutrínók, amelyek megjelenése a neutrínócsillagászat kezdetét jelentette.
1998. június 5-én elképesztő kijelentés hangzott el egy sajtókonferencián a japán Takayamában. A Kamioka Neutrínómegfigyelőben dolgozó 120 amerikai és japán fizikus kísérlettel igazolta, hogy a mindeddig megfoghatatlan neutrínónak mégis van tömege. A felfedezés távoli területeken is érezteti hatását, hiszen megváltoztathatja az anyagról, a világegyetem keletkezéséről és annak sűrűségéről alkotott eddigi elképzelésünket. A japán-amerikai vegyes csapat a neutrínók tömegével kapcsolatos következtetését abból a kísérletből vonta le, amellyel igazolni tudták, hogy a neutrínók valóban „átöltöznek”: az elektron típusú neutrínó müon vagy tauon típusúvá válik. A kvantumelmélet szerint erre csak olyan részecske képes, amelynek tömege van. A neutrínó tényleges tömegét még nem tudták megmérni. De a puszta tény, hogy rendelkezik ilyennel, azt jelenti, hogy megtaláltuk a világegyetemből hiányzó tömeg egy részét. Mi is ez a „hiányzó tömeg”?
A csillagok galaxisokba tömörülnek. Egy galaxisban a csillagok a kölcsönösen kifejtett tömegvonzás miatt maradnak együtt. Ha egyre távolabb nézünk az űrben, meglepődve vehetjük észre, hogy a galaxisok nem véletlenszerűen helyezkednek el. Egy struktúra látunk kibontakozni. Az IBM kutatási központjában és a Yale Egyetemen dolgozó Benoit Mandelbrot néhány éve bebizonyította, hogy a galaxisok szerkezete egy fraktálhoz hasonlít - egy bonyolult elrendezéshez, amely határozottan nem véletlenszerű, még akkor sem, ha egyes pontokról szemlélve úgy tűnne. A galaxisok galaxishalmazokat alkotnak, amelyek szuperhalmazokba állnak össze, és így tovább, egyre nagyobb léptékben. A galaxishalmazok között nagy üres űrbuborékok vannak, amelyek mérete fényévmilliókban mérhető.
Az 1930-as évek végén a csillagászok észrevették, hogy a világegyetem „csomós”, vagyis, hogy a galaxisok halmazokat alkotnak. Az évek során azután egyre több adat gyűlt össze az anyag eloszlásáról az egyre nagyobb, ismert térben. 1986-ban a Harvard-Smithson Asztrofizikai Központ három kutatója: Margaret Geller, John Huchra és Valerie de Lapparent összeállította az északi félteke égboltjának mintegy egy 6000 galaxist feltüntető térképét. A térkép középpontja a Föld, a „tortaszelet” csúcsa, és a kiterjedése 650 millió fényév. A szerkezet szemmel láthatóan nem egyenletes, és felsejlik benne egy fraktáltermészetű elrendezés. Honnan származhat?
A világegyetem létrejötte utáni első pillanatokban történt kvantumhullámzások valószínűleg buborékokat alakítottak ki az anyagban, amelyek együtt nagyobbodtak a világegyetem tágulásával. A világegyetem anyagai által kölcsönösen kifejtett tömegvonzás alakíthatta ki a ma megfigyelhető galaxishalmazokat és -falakat. De amikor a tudósok a galaxisokon belüli gravitációs hatásokat kezdték vizsgálni -tehát a galaxisokat összetartó erőket -, egy rejtélybe ütköztek.
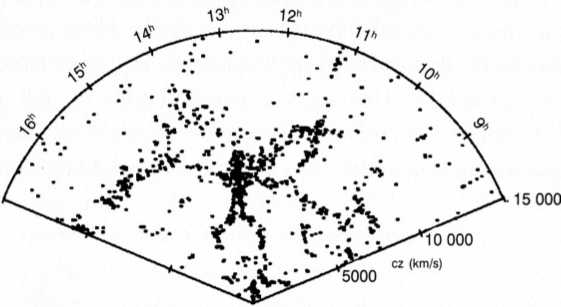
Az Asztrofizikai Központ (CfA) © John Huchra és Margaret Geller vázlata az északi félteke égboltjának egy szeletéről
Minden, az asztrofizikusok által tanulmányozott galaxisban sokkal kisebbnek bizonyult a látható anyag (csillagok vagy gáz és por) tömege, mint amennyi a számítások szerint ahhoz kellene, hogy a galaxist a gravitáció egyben tartsa. Ebből csak arra lehet következtetni, hogy a galaxisok át vannak itatva valamilyen ismeretlen anyaggal, amely a galaxisok tömegének 90%-át teszi ki! Ezt a titokzatos, láthatatlan, de mégis jelen lévő anyagot „sötét anyagnak” nevezték el. Ez az anyag egyelőre még ismeretlen a tudomány számára. Nem barionikus
- tehát nem atomokból és szubatomi részecskékből áll - hanem valami eddig soha nem látott. A sötét anyag természete a csillagászat egyik legnagyobb rejtélye.
Az anyag tulajdonságaiban rejlik a kozmológia kulcsa, világegyetemünk vajon az anyag által meghatározott, vagy van valami, aminek az anyagnál is fontosabb szerepe van a világegyetem múltjának és jövőjének meghatározásában? Ez az egyik legnagyobb kozmológiai kérdés. Vannak kozmológusok, akik kitartóan keresik a világegyetem további „hiányzó anyagát” (a sötét anyagon kívülit, amelynek létezésére a galaxisokra gyakorolt hatásából lehet következtetni). Azért biztosak a „hiányzó anyag” létezésében, mert ők a világegyetemet laposnak, tehát euklideszinek tekintik. Ahhoz, hogy ez igaz legyen, sokkal több anyagra van szükség a világegyetemben, mint amennyi látható, vagy amennyi a galaxisok gravitációjának tanulmányozásából kiszámítható. A legtöbb felfúvódó és hasonló kozmológiai elmélet „sík” geometriai modellje azon a feltételezésen alapszik, hogy a világegyetem sűrűségének van egy kritikus értéke, és hogy ha a valóban mért tömegsűrűség ezzel megegyezik, akkor a geometria „sík”.
Az ilyen nézeteket valló elméleti kutatók a hiányzó anyagot keresik. A neutrínó tömegének felfedezésekor felmerült, hogy esetleg ezzel megtalálták a hiányzó anyagot. De még ha a neutrínóknak van is tömegük - és jó sok neutrínó van szerte a világegyetemben - össztömegük akkor sem fedné le a hiányzó anyagmennyiséget. Tehát vagy vannak még valamilyen eddig ismeretlen, rejtett anyagok a világegyetemben, vagy a világegyetem tömegsűrűsége túl kicsi. Ha a világegyetem tömege kisebb a kritikusnál, akkor tágulásának semmi nem szab határt. Ha nagyobb, akkor a világegyetem összeomolhat a gravitációnak köszönhetően, és bekövetkezik a „nagy reccs”, és utána talán majd keletkezik egy új világegyetem egy újabb ősrobbanásból.
A világegyetem tömegsűrűsége, az, hogy a világegyetemet az anyag vagy valami más határozza-e meg, és hogy megvan-e a hiányzó anyag: ezek a kérdések mind egy fontos fogalomhoz vezetnek: a világegyetem átfogó geometriájához. Einstein eredeti téregyenletében azt tételezte fel, hogy a világegyetemet az anyag határozza meg. A kozmológiai állandó bevezetésével megnyílt egy másik magyarázat lehetősége. Az új modell magyarázatul szolgált mind a tömeg, mind a gravitáció hatására, és egy új jelenségre is - egy ismeretlen erő hatására, amely a gravitáció ellen dolgozik, az űr valamilyen
energiájaként van jelen a világegyetemben. Einstein egyenletei mindenképpen a tér természetével, azaz geometriájával foglalkoznak.
14. A világegyetem geometriája
Ezen a ponton fel kell tennünk egy érdekes kérdést: milyen a világegyetem átfogó geometriája? Tudjuk, hogy lokálisan, egy csillag vagy más nagy tömegű test közelében a tér görbül. A tér gömb alakban görbül az ilyen testek körül, amint ezt a napfogyatkozási expedíciók bizonyították. De milyen a világegyetem egészének alakja? Közvetlen összefüggés van a geometria és a matematikai egyenletek között. Einstein téregyenlete alapján képet alkothatunk a világegyetem geometriájáról.
Ha ismerjük a világegyetem geometriáját, meg tudjuk jósolni a jövőjét. A matematikusok három lehetséges geometriát tartanak a világegyetem egészére alkalmazhatónak. Az első a (lapos) sík, euklideszi geometria. Az euklideszi világegyetem térgörbülete definíció szerint 0. A görbület fogalmát Gauss vezette be, és a k betűvel jelölte. Ehhez azt kellett feltételeznie, hogy a világegyetem felületének görbülete állandó. Egy lapos világegyetemben tehát a görbület: k = 0. A nemnulla állandó görbülettel rendelkező felületek kétfélék lehetnek. A görbület lehet pozitív (k = +1) vagy negatív (k = -1). Egy k = +1 görbületű felület zárt. Kétdimenziós felület esetében ez egy gömböt jelent. Ha egy felület görbülete k = -1, akkor az nyílt, és geometriája hiperbolikus, mint a Bolyai-Gauss-Lobacsevszkij modellé. Itt a kétdimenziós felület egy
pszeudogömb külső felülete. A három állandó görbületű kétdimenziós modellt látjuk az alábbi ábrán.58

Tekintsük most a négydimenziós téridőt, vagy úgy is fogalmazhatunk, hogy nézzük meg, hogyan fejlődött a háromdimenziós világegyetem az időben - mindezt a három lehetséges állandó görbületű geometria szempontjából. Meg fogjuk látni, hogy alakjuk alapján a kozmológusok miért a „lapos”, „zárt” és „nyílt” jelzőkkel határozzák meg a lehetséges világegyetemeket. Ehhez újra megvizsgáljuk Einstein téregyenletét, amely meghatározza a világegyetem geometriáját.
Einstein kozmológiai állandó nélküli egyenlete:

A négydimenziós téridőben a relativitáselmélet különleges metrikájával határozhatjuk meg a távolságokat. Ebben a metrikában a negatív görbületű hiperbolikus térhez leginkább egy nyeregfelület hasonlítható.


viszont nincsen elég anyag a világegyetem összetartásához - az örökké tágulni fog. Lapos világegyetem esetén is ez a helyzet, de ekkor a tágulás mértéke egyre csökken.59
A kozmológusok el is nevezték a két sűrűség (a világegyetem egy adott pillanatban létező tömegsűrűsége, p és a fenti kifejezés szerinti kritikus sűrűség) arányát: ez Q (ómega).
Az ómega a világegyetem geometriájának kulcsa. Ha nincsen kozmológiai állandó, a következő a helyzet. Ha Q = 1, akkor a sűrűség éppen megegyezik a kritikus sűrűséggel, és a világegyetem lapos - tágulása végtelen, de egyre lassuló.
Ha Q > 1, akkor a világegyetem tömegsűrűsége nagyobb a kritikus sűrűségnél, ami egyben tartja a világegyetemet, és a világegyetem tágulása lassul. Ekkor több tömeg van jelen, mint amennyi a tágulás lelassításához szükséges, és a világegyetem tágulása egy szép napon egyszer csak megáll, és a folyamat megfordul az elkerülhetetlen „nagy reccs” irányába, amely azután mindent elnyel. Utána elképzelhető egy újjászületés, egy új ősrobbanás, és minden folytatódik tovább: mindig új világegyetem születik az előző poraiból.
Ha Q < 1, akkor a világegyetem tömegsűrűsége kisebb a kritikus sűrűségnél. Nincsen jelen elég tömegmennyiség a tágulás megfékezéséhez és az összeomláshoz, a világegyetem tágulása örökké folytatódik. Geometriája hiperbolikus.
A világegyetem sorsa a fenti három esetben akkor is különböző lesz, ha a kozmológiai állandó értéke nem nulla, de akkor nem csak Q, hanem X értékétől is függ.
A világegyetem geometriája attól függ, hogy a háromdimenziós világegyetem hogyan alakul az időben. Egy gömb alakú világegyetem, amely kitágul, majd összeomlik -ahol Q > 1 - ciklois görbét ír le, ha a vízszintes tengelyen az időt ábrázoljuk (itt a világegyetemet minden egyes pillanatban egy kör jelöli; az egyik térbeli mennyiséget nem ábrázoljuk, hogy az ábra beleférjen a könyvbe). Itt látható egy ilyen világegyetem képe.

Egy lapos világegyetem, tehát egy olyan, ahol Q = 1, egyre lassulva tágul.
Egy Q < 1 tulajdonságú világegyetem egyre gyorsulva tágul, ahogyan azt az alábbi ábra mutatja.

De mi van akkor, ha van még valami a világegyetemben, ami hatással van a tágulásra, a geometriára - az egész világegyetem sorsára? Ha van valamilyen „fura energia” valahol az űrben, amelyet nem látunk, érzünk vagy észlelünk, de amely mégis hatással van a téridő szövetére, és amitől az gyorsabban tágul -akkor az anyag és az általa keltett gravitációs erő nincsenek egyedül. Kell lennie még valaminek.
Ha a tudósok ezt az irányt akarták követni, meg kellett változtatniuk a Q definícióját. Ennek a paraméternek, amely a világegyetem kulcsának tekinthető, valamilyen módon magában kellene foglalnia ezt az ismeretlen tényezőt is. A kozmológusok azt találták ki, hogy több részre osztják a teljes Q-t: egy anyaggal kapcsolatos részre, és egy másikra, amelyet mintegy próbaképpen Einstein jó öreg kozmológiai állandójához kötöttek. Így a világegyetem geometriáját meghatározó paraméter két része: Q = Qm + Qa. Bár Q meghatározza a világegyetem geometriáját, a világegyetem sorsa szinte kizárólag Qa-íóI, a „fura energiától” függ. Einstein kozmológiai állandójának energiája olyan nagy erejű lehet, hogy ez esetleg a Qm értékétől függetlenül, önmagában is elég ahhoz, hogy a világegyetem korlátlanul táguljon tovább.
A Szupernóva Kozmológiai Projektet Saul Perlmutter és kollégái 1988-ban azért kezdték el, mert lehetségesnek tartották, hogy meg tudják majd határozni a világegyetem geometriáját és sorsát. Csillagászati megfigyelésekkel próbálták az ómega paramétereket meghatározni. Ehhez a „normálgyertyák” (Ia típusú szupernóvák) fénygörbéjét tanulmányozták. Végül a leleményes csillagászok a vártnál is közelebb jutottak a megoldáshoz. Többévi megfigyelés és számítás után világossá vált előttük, hogy valamilyen, a tudomány által soha nem tapasztalt nagyságú erő van jelen a világegyetemben. Az Qm értéke a vártnál jóval kisebbnek bizonyult. A robbanó csillagok a kozmosz túloldalán különös, fantasztikus dolgot bizonyítottak: nincsen elég tömeg a világegyetemben ahhoz, hogy bármely tömegalapú elmélet igaz legyen, és egy láthatatlan erő lök egymástól egyre gyorsabban szét mindent. Einstein kozmológiai állandója és az ehhez kapcsolódó Qa mérhetetlen túlsúlyba került. De akkor milyen is a világegyetem?
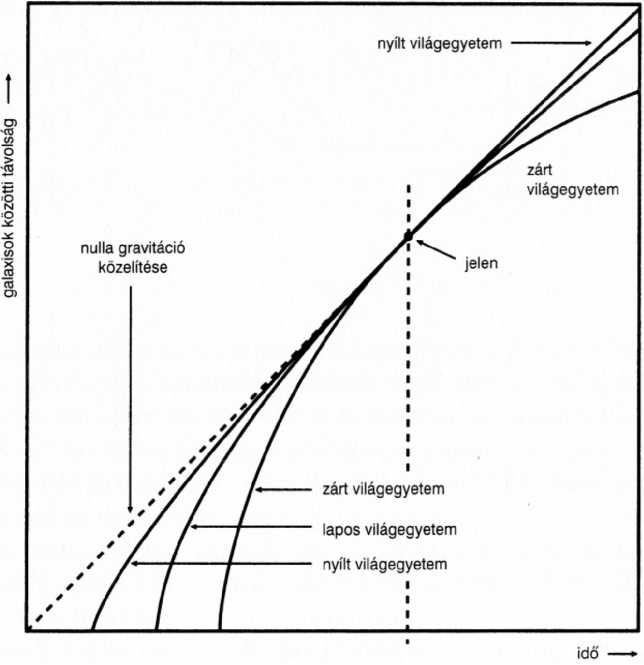
A világegyetem három modellje, illetve lehetséges sorsa
15. Illinois állam Batavia városa, 1998. május 4.
Paul Steinhardt, a kozmológia fiatal tudományának egyik legfiatalabb létrehozója 1952-ben született, és 1978-ban doktorált a Harvard fizika szakán. Részecskefizikát tanult, de hamarosan a kozmológia felé fordult. Steinhardt a Pennsylvaniai Egyetem tanára lett, és ott Guth felfúvódó modelljét tanulmányozta. Sok más tudóssal ellentétben Steinhardt nem vette készpénznek a felfúvódási modellt - meg szerette volna őrizni tárgyilagosságát, és csak az adatok (csillagászati megfigyelések, a kozmikus sugárzás mérési adatai és más fizikai adatok) alapján akart dönteni. Hamarosan rájött, hogy az érdekes és ígéretes felfúvódási modellel elméleti problémák vannak. Ezek közül az első és legfontosabb az volt, hogy nem ismerjük, mi az az erő, amely a felfúvódást megállítja, hogy következhessen az a szelídebb ütemű tágulási időszak, amelynek mi is tanúi vagyunk.
Paul Andy Albrecht doktoranduszhallgatóval dolgozott, és együtt jöttek rá a megoldásra. Úgy vizsgálták újra Guth felfúvódó modelljét, hogy feltételezték, a tágulás - és az azt okozó erőtér - lassabban nő, amely esetben még mindig a felfúvódással magyarázhatóak a fizikai jelenségek, de ugyanakkor megvan arra is az esély, hogy a folyamat egy bizonyos ponton megáll. Utána egy kiterjesztett felfúvódásnak nevezett modellt dolgozott ki, ahol egy másik erőtér is ellensúlyozza a gravitációs hatást. Elmélete szerint a világegyetem korai időszakában a gravitációs állandó értéke még nem annyi volt, mint ma. Így Einstein téregyenletének G tagja nem volt konstans a világegyetem hajnalán. Ekkor - a Planck-korszakban, amely az ősrobbanás utáni 10-44 másodperces időszakot jelenti - még érvényesültek a kvantumjelenségek. A világegyetemnek ebben az első pillanatában a kvantummechanika - a nagyon kicsi elmélete -határozta meg, hogy mi fog történni a világegyetemben, és Einstein klasszikus relativitáselmélete még nem lépett érvénybe. Új tudományterületre volt szükség. A kvantumkozmológia keletkezőben lévő tudománya sokat köszönhet Paul Steinhardtnak.
1995-ben Steinhardt megpróbálta összevetni a különböző forrásokból származó fizikai és csillagászati eredményeket, amelyek érzése szerint mind abba az irányba mutattak, hogy a világegyetem tágulása gyorsul. Ez viszont természetellenesnek tűnt. Miért működne így a világegyetem, ha egyszer a világegyetem egyetlen nagy hatótávolságú erője, a gravitáció elmélete szerint az ősrobbanáskor kezdődő tágulásnak lassulnia kellene, hiszen a világegyetemben jelen lévő anyagok vonzzák egymást?
A legújabb kozmológiai eredmények ismeretében 1997 szeptemberében Paul Steinhardt úgy dönt, hogy itt az ideje megbeszélni, mi is zajlik a világegyetemben, és összehív egy nagy találkozót, amelyen részt venne több, a kozmológiához kapcsolható tudományág képviselője is: csillagászok, asztrofizikusok, kísérleti fizikusok, részecskefizikusok, alkalmazott matematikusok és mások. Vajon a különböző területeken dolgozó tudósok hogyan értelmezik az új eredményeket, és mire következtetnek belőlük? Steinhardt úgy gondolta, hogy a legjobb helyszín a Fermi Nemzeti Részecskegyorsító Laboratórium (röviden: Fermilab) lesz az illinoisi Bataviában. Itt már több fontos kísérletet végeztek annak érdekében, hogy megvizsgálják, hogyan viselkedhetett az anyag a világegyetem kezdetén. Az itt dolgozó Joshua Frieman és Steinhardt együtt kezdtek az 1998. májusi konferencia szervezéséhez.
A Nature folyóiratban 1998 januárjában megjelent egy cikk Perlmutter és a Szupernóva Kozmológiai Projekt adatairól, amelyeket nyolc szupernóva megfigyelése alapján gyűjtöttek.60 Az adatokból úgy tűnt, hogy a térben és időben távolabbi galaxisok, például a csoport által tanulmányozott nyolc, lassabban távolodnak tőlünk, mint a közeli galaxisok. A csoport előtt állt még hatvan galaxis Ia típusú szupernóváinak elemzése. Vajon a fent említett jelenséget támasztják majd alá az újabb adatok? Ha igen, ez azt jelenti, hogy a világegyetem a mi időnkben gyorsabban tágul, mint régebben.
Az Amerikai Csillagászati Társaság 1998. januári, washingtoni ülésén Perlmutter projektje bemutatta eredményeit, amelyek arra utalnak, hogy a világegyetem egyre jobban tágul. A rivális Harvard-Smithson szupernóva-kutató csoport később arról számolt be, hogy egyes eredményeik igazolják Perlmutter feltevését. Két princetoni csapat, Ruth Daly, illetve Neta Bahcall vezetésével, szintén hasonló eredményekről számolt be. Ők is azt állították, hogy a világegyetem össztömege kevés a tágulás korlátok közt tartásához.
Neta Bahcall Izraelben született és nevelkedett. Matematikát és fizikát tanult a Héber Egyetemen, és 1964-ben nukleáris fizikából diplomázott a Weizmann Intézetben. Ugyanebben az évben ismerkedett meg jövendőbelijével, John Bahcall-lal, aki a Caltech (a Kaliforniai Műszaki Egyetem) fizikusprofesszoraként meglátogatta a Weizmann Intézetet. A következő évben összeházasodtak, és Neta a Caltechen nukleáris asztrofizikai doktori értekezésén dolgozott William Fowler felügyelete alatt (aki néhány évvel később Nobel-díjat kapott). Neta kutatásai a csillagok belsejében bekövetkező nukleáris reakciókra összpontosultak, amelyeknek a csillagok a fényüket köszönhetik. 1970-ben megkapta a doktori fokozatot a telavivi egyetemtől. Ekkor már nagyon érdekelte a csillagászat, és több közös kutatási programban is részt vett a Caltech asztrofizikusaival, akik kvazárokat és más csillagászati jelenségeket tanulmányoztak.
1972-ben a Bahcall házaspár a nemrég elkészült az izraeli negev-sivatagi Wise Csillagvizsgálóban nézte a csillagokat. Szállásuk a csillagvizsgáló közelében volt, de nem volt kire hagyni a gyerekeket, így magukkal hozták a hároméves Safit és a még nem egészen egyéves Dant, és a csillagvizsgálóban talált fiókokban ágyaztak meg nekik. A gyerekeik már aludtak, amikor Neta és John Bahcall felfedezte az első pulzáló kettős
optikai rendszert, amely ugyanaz, mint az első, műhold által érzékelt pulzáló röngtenforrású kettős rendszer. A tömör objektum, amelynek a gáza a röntgensugarakat kibocsátja, egy pulzár - az első kettős pulzár. Ez nagy szenzáció volt a csillagászatban. Ez volt az új csillagvizsgálóban tett első felfedezés, és az izraeli állam Neta Bahcallt Az év tudósnőjének választotta.
Bahcallék Princetonba költöztek, ahol Neta most az egyetem asztrofizika-professzora, John pedig a Felsőfokú Tudományok Intézete (Institute of Advanced Studies) természettudományi professzora, őt 1998-ban Clinton elnök a Nemzeti Tudományos Éremmel tüntette ki. Neta Bahcall hat évig volt az Űrtávcső Tudományos Intézet (Space Telescope Science Institute) tudományos hivatalának vezetője, ahol eldöntik, hogy a Hubble-űrtávcső milyen fontos csillagászati megfigyeléseket tegyen. Az évek során érdeklődése egyre inkább a kozmológia felé fordult, és azt kutatta, hogy az asztrofizikai felfedezések segítségével hogyan fejthető meg a világegyetem szerkezete, kezdete, kora, és további sorsa. Neta Bahcall éveken keresztül tanulmányozta a világegyetem nagyléptékű szerkezetét, és megpróbálta megválaszolni a kozmológia nagy kérdéseit. Kutatása sok eredményt hozott, és felfedezései elismeréseképpen 1997-ben az Egyesült Államok Nemzeti Tudományos Akadémiájának tagjává választották.
Az Amerikai Csillagászati Társaság 1998. januári ülésén Neta Bahcall bemutatta eredményeit, amelyek a kollégáival együtt végzett vizsgálatokon alapultak, és amelyek célja az volt, hogy több, egymástól független módon lemérik a világegyetem tömegét. A kutatók galaxishalmazokban vizsgálták a világegyetem anyagának fejlődését és eloszlását. Az egyik módszer Einstein gravitációslencsehatásán alapult. Itt a távoli galaxisok fényének elgörbülését vizsgálták, ami a Föld és köztük lévő galaxisok környékén játszódik le; a fényelgörbülés mértéke alapján meg lehet becsülni a közelebbi galaxis tömegét. Más módszerek a galaxisokban megtalálható forró gázok vizsgálatából indultak ki, vagy a sebességből, a vöröseltolódásból, illetve a tömeg és a fény arányából. Bahcall tanulmányozta a galaxisok fényudvarát, ahol kutatása szerint a világegyetem sötét anyagának nagy része elhelyezkedik. Neta Bahcall arra a következtetésre jutott, hogy a világegyetem sűrűsége csak mintegy 20%-a annak a sűrűségnek, amely megállítaná a tágulás ütemét, de nem vezetne el az összeomláshoz. Ezt az értéket több különböző kutatási módszerrel, egymástól függetlenül érték el. A következtetés helytelenségének valószínűsége körülbelül egy a millióhoz.61
A sajtóban sok szó esett Perlmutter, Bahcall és társaik meglepő felfedezéseiről. Az új tények megragadták a világ képzeletét. Úgy látszott, hogy mindenki - tudósok és laikusok egyaránt - „korlátos” világegyetemet szeretne, esetleg valami, Einstein statikus modelljére emlékeztető világot. Ha a világegyetem valóban tágul, és nem változatlan - és ezzel Hubble már az 1920-as években meglepte a világot - akkor az emberek legalább azt szerették volna látni, hogy a világegyetem a kiterjedés és az összehúzódás között oszcillál. Egy felváltva kiterjedő és összehúzódó világegyetemben megmarad a végső megújulás esélye, ha a félelmetesen távoli jövőben is. Egy korlátlanul táguló világegyetem, amelyben remény sincsen az újbóli összehúzódásra, majd egy újabb ősrobbanásra, nem túl biztató forgatókönyv. Ez lehetett az egyik oka annak, hogy a Fermilabben tartott májusi összejövetelen a sajtó is jelen volt.
A Fermilabben összegyűlt tudósokat még a végtelenné táguló világegyetemnél is fontosabb kérdés foglalkoztatta: a fizika sorsa. A tudósoknak azzal a szinte elkerülhetetlen következtetéssel kellett szembenézniük, hogy a világegyetemben valami nagyon furcsa dolog történik, valami, amit egyikük sem ért. A természet egy ötödik erőt is csatasorba állított, de ezt az erőt még senki nem tapasztalta. Ez az érzés, amelyben a fizikusok, a részecskeelmélettel foglalkozók és a csillagászok mindannyian osztoztak, egyre erősödött az eredmények elemzései hallatán. A tudósnak az a dolga, hogy kételkedjen; bizonyítékokat szerettek volna, mielőtt elvetik a régi elméleteket, hogy helyet készítsenek az újnak. Amikor mind együtt voltak, összesen hatvan tudós, megkezdődtek az előadások.
William Press, a Harvard-Smithsonian csoport egyik csillagásza, magára vállalta az ördög ügyvédjének szerepét csapatával és a Berkeley-csapattal szemben, miután a két szupernóva-kutató csoport bemutatta eredményeit. „Mi van, ha az eredmények nem igazak?” Ez volt a nagy kérdés. A másik csapat két tagja, Saul Perlmutter és Robert Kirshner az adatok védelmére kelt, amelyekkel kapcsolatban többféle kérdés is felmerülhetett. Először is, a szupernóvák valóban normálgyertyának tekinthetők?62 Honnan tudjuk, hogy egy hétmilliárd éve bekövetkezett Ia típusú szupernóva ugyanolyan fénygörbével rendelkezik, mint egy csupán félmilliárd éves? És ott volt még annak a korrekciónak a kérdése is, amelyet a csapatok a fényadatokkal kapcsolatban kényszerültek végezni azok összehasonlíthatósága érdekében. Jól sikerült a korrekció? Végül pedig ott volt az a meglepetés, amely a tanulmányozott galaxisokban érte a kutatókat: a por hiánya. Miért nem találtak port?
A két csapat hosszan tárgyalta a technikai részleteket, és láthatólag mindenki megelégedésére tisztázták a kényes pontokat. Próbaszavazást tartottak, és a tudósok nagy többsége tudományosan meggyőzőnek fogadta el az új adatokat. Nem volt tehát menekvés az elkerülhetetlen, régóta kísértő kérdés elől: mi okozza a világegyetem gyorsuló tágulását? A világegyetem össztömege inkább össze kellene, hogy húzza az egészet. Az ősrobbanáskor kezdődött tágulásnak le kellene lassulnia a világegyetem galaxisaiban elhelyezkedő anyag tömegétől. De az 1998 májusában a Fermilabben bemutatott bizonyítékok világosan azt mutatják, hogy ez mégsem így van. A világegyetemben nincsen elegendő tömeg ahhoz, hogy az lelassítsa a tágulást, sőt ellenkezőleg: azt valamilyen titokzatos erő gyorsítja. Valamilyen negatív nyomás van a vákuumban, valami olyan, ami idegen a tudomány számára. De vajon valóban így van-e?
„Van valami fura energia a világegyetemben” - írta a Fermilabben dolgozó Michael Turner a jegyzetfüzetébe. A szöveg köré csillagokat is rajzolt, fejüket vakaró embereket és a görög nagy A betűt. 1998. május 5-én rajza megjelent a New York Times tudományos mellékletének címlapján.
- Ami elég jó volt Einsteinnek, - mondta Turner a kozmológiai állandóra gondolva - legyen elég jó nekünk is.
De az új elméleteket, például a felfúvódási elméletet valló kozmológusok még egy lépéssel tovább akartak menni. A kozmológiai állandó elvileg képviselheti azt a titokzatos természeti erőt, amely kifelé nyomja a teret, dacolva a gravitációval, és a világegyetemet a végtelenségig tágítja. De a felfúvódási elmélet szerint egyszer régen, az ősrobbanás utáni első pillanattöredékben, jelen volt egy hasonló erő a világegyetemben, amely miatt a világegyetem exponenciális ütemben terjedt ki. Tehát a kozmológiai állandónak le kell írnia ezt az időszakot is. De van itt egy kis gond. A láthatatlan erő nagysága más volt abban a bizonyos rövid, ősi pillanatban, mint ma. Mit kezd a tudomány egy változó értékű A-val?
Ezt a fontos kérdést, amely megoldaná a modern kozmológia sok rejtélyét, legtermészetesebben úgy válaszolhatnánk meg, ha kozmológiai állandó helyett kozmológiai változót használnánk, amely az idő, vagy Einstein egyenlete más változóinak függvénye lenne. De ennek pontos képletét senki sem tudja. Einstein már több mint négy évtizede halott, és úgy látszik, azóta senki nem vette a bátorságot, illetve nem támadt a megfelelő ösztönös megérzése, vagy nem volt elegendő tudása ahhoz, hogy megváltoztassa az egyenletet, amelyet pedig ő maga is megváltoztatott, amikor először bevezette a kozmológiai állandót.
Einstein követői, az általános relativitáselmélettel foglalkozó fizikusok idejüket Einstein téregyenletének megoldásával töltik. Ehhez a régi és új módszerek teljes fegyvertárát felvonultatják: számítógépen futtatott numerikus eljárásokat, vagy éppen komplex differenciálegyenletek elméleti levezetéseit. De valahogy nem akaródzik nekik az új eredményekhez igazítani Einstein egyenletét.
Einstein téregyenlete szent és sérthetetlen. Az egyenletet a nagy mester alkotta. Minden tenzornak, minden állandónak, minden kis elemnek célja van. A tenzoregyenlet a természet törvényeit rögzíti. Ezek a törvények nem változnak akkor sem, ha az ember egy fizikai folyamatot más szemszögből vagy más koordináta-rendszerben vizsgál. Határhelyzetben pedig a tenzoregyenlet kiadja az egyszerűbb newtoni törvényeket, amelyek nem relativitási környezetben használhatóak.
Einstein egyenletébe bele tudta foglalni a később már fekete báránynak tekintett mennyiséget a metrikus tenzor ravasz megcsavarásával; csak egy kicsit kellett még görbítenie a téren, és az egyenletbe belefért az állandó úgy hogy egyenletének megmaradtak azok a fontos tulajdonságai, amelyeken évekig dolgozott.
De egy puszta állandóból változót kreálni? Erre talán még maga a nagy mester sem lett volna képes. Így azoknak a kozmológusoknak, akik a világegyetem „fura energiáját” úgy szerették volna megmagyarázni, hogy közben a felfúvódási elméletet is megtartják, más megoldás után kellett nézniük: egy új elméletet kellett kidolgozniuk.
Paul Steinhardt volt az egyik alternatív modell atyja. Kvintesszenciának nevezte ezt el Arisztotelész ötödik természeti eleme után, ezzel utalt a természetben feltételezett ötödik erőre. A fizikusok által ismert első négy erő a gravitáció, az elektromágnesesség, illetve az erős és gyenge nukleáris erők. A kvintesszencia, amelyet még soha senki nem tapasztalt, lenne tehát az ötödik. Steinhardt most azon dolgozik, hogy hogyan építse be a kvintesszenciái Einstein téregyenletébe. Függetlenül attól, hogy melyik elmélet oldja majd meg a problémát, Steinhardt találóan foglalta össze a kozmológusokat most nagyon is foglalkoztató rejtélyt.
- A világegyetemben egy negatív nyomás működik - mondta nekem. - Egy dolog azonban már biztos, és ez az, hogy Qm < 1. Mit jelent ez? Görbületet, kvintesszenciát, A-t? Nem tudjuk, de bármi is az, hatással van a fizika alapjaira.
Einstein kozmológiai állandója életben maradt, még ha megalkotója mossa is kezeit. Steven Weinberg monográfiájában elmeséli a nehezen megfogható konstans kalandjait.63 Weinberg megmutatja, hogy az állandó Einstein egyenletében a vákuum teljes hatásos energiájához A/8nG-t ad hozzá. Az a kérdés, hogy az állandó adja-e a vákuum teljes energiáját, vagy van esetleg valami más, ami kifelé nyomja a világegyetemet. És ha a teljes felelősség a kozmológiai állandóé, akkor az vajon mekkora?
Az 1960-as és 1970-es években a részecskefizikusokat azért érdekelte a kozmológiai állandó, mert meg kellett becsülniük az üres tér energiaszintjeit ahhoz, hogy megkülönböztethessék az ilyen energiát a gyorsítókban vizsgált részecskék energiájától. De akármilyen keményen próbálkoztak, az üres térben várt energia mennyisége nem egyezett semmilyen értékkel, amelyet a kozmológiai állandó segítségével számoltak ki. A részecskefizikusok fel is hagytak ezzel a törekvéssel. Ugyanebben az időben a kozmológusok viszont újra felfedezték a száműzött állandót, és megpróbálták saját céljaikra használni. Az 1960-as években felmerült egy halasztást nem tűrő, ugyanakkor gyors megoldást nem ígérő kozmológiai kérdés: a kvazárok problémája.
A kvazárok (más szóval: kvázi csillagszerű objektumok) rengeteg rádióenergiát bocsátanak ki, amelyet a csillagászok észlelnek. Megmagyarázhatatlanul sok olyan kvazárt találtak, amelynek a vöröseltolódási értéke kb. z = 1,95. Ezek tőlünk térben és időben is igen távol helyezkednek el, és körülbelül ugyanakkor keletkezhettek (ezt vöröseltolódásuk alapján tudjuk, amely jelzi a tőlünk való távolodásuk sebességét). De miért? A kozmológusok tudták, hogy a jelenség könnyen megmagyarázható lenne, ha a világegyetem valamilyen okból nem tágult volna túl sokat a kvazárok keletkezésének idejében, hiszen akkor körülbelül ugyanolyan távolságra helyezkedtek volna el tőlünk. A világegyetem tágulását lelassítani vagy megállítani viszont mi tudná jobban, mint a kozmológiai állandó? Több kozmológus is éveket töltött el ennek a rejtélynek a tisztázásával.64
A részecskefizikusok nem adták fel. Most az elektrogyenge-elmélet (más néven a standard modell) alapján próbálták megválaszolni a spontán szimmetriasértéssel kapcsolatban felmerülő kérdéseket. Szimmetriasértésnek nevezzük azt a folyamatot, amikor a különböző típusú részecskék keletkeztek a világegyetem kezdeti szakaszában. A részecskefizikusok szerint mivel egy elektron különbözik egy kvarktól, keletkezésükkor egy szimmetria tört meg. A tudósok egy olyan problémával szembesültek, amelyben a sűrűség értéke valahogyan negatív lett. Ekkor úgy tűnt, hogy ha a A kozmológiai állandót egyenleteikbe illesztik, akkor kiesik egy fontos tényező, és ez meghozza az eredményt. Ennek viszont az lett volna a mellékhatása, hogy a távoli múltban a A értéke valószínűleg nagyon nagy volt. Ezzel nem tudtak mit kezdeni, amíg Guth ki nem találta a felfúvódó világegyetem-modellt. Ha a kozmológiai állandó valóban olyan nagy volt az ősrobbanás utáni első pillanatban, akkor ez lehetett az az erő, amely a világegyetem exponenciális tágulását okozta. Így ha a kozmológiai állandót belevesszük az egyenletbe, értékét nagyon gondosan kell megválasztanunk.
A tudományban mindig kellenek friss, új elméletek, amelyekhez új matematikai eszközökre van szükség. Einstein egyenletét nem elég próbálgatásos módszerrel megközelíteni. A nevezetes egyenlet nagyon is jól teljesített az eltelt évek során, sok új fizikai felfedezést köszönhetünk az egyenletből következő előrejelzéseknek. De ha valaki a kozmológiai állandót is tartalmazó egyenletből próbál kiindulni, vagy a relativisztikus egyenletet kvantumelmélettel próbálja párosítani, akkor kevés sikerrel jár. Az emberiség egyszerűen még nem érti eléggé a bűvös egyenletet.
1985-ben egy új elmélet született, amely ígéretesnek tűnt többféle fizikai probléma megoldásának szempontjából is: a szuperhúrelmélet. Az elmélet a téridő négy dimenziója helyett tizeneggyel dolgozik abban az értelemben, hogy a világegyetemet modellező szuperhúrelmélet egyenletei tizenegy dimenziót használnak. Az elméletnek érdekes eredményei vannak, de még nem oldotta meg Einstein kozmológiai állandójának problémáját. Az 1980-as évek végén a matematikusok kidolgoztak egy másik szuperhúrelméletet, amelyben két térváltozót tömörítettek. De amikor megpróbálták az eredményt a négydimenziós téridőre kiterjeszteni, a módszer csődöt mondott, és az építmény összedőlt.
1996 decemberében a londoni lapok arról számoltak be, hogy Stephen Hawking, a híres kozmológus egy „matematikai gyorstalpalóra iratkozott be”.65 Egy oxfordi matematikaprofesszor előadássorozatot tervezett a négydimenziós felületek topológiájáról, és kapcsolatukról az általános relativitáselmélettel és a kvantumelmélettel. A téma több kozmológus érdeklődését is felkeltette, köztük Hawkingét. Úgy tűnt, hogy a matematikus egy érdekes kapcsolatot fedezett fel a négydimenziós felületek és az „egzotikus”, csak a négydimenziós terekre jellemző fizikai jelenségek között. Sir Roger Penrose, a nagy hírű topológus, aki szakterületének már több elvont matematikai felfedezését alkalmazta a fizikai problémák megoldására, így nyilatkozott erről az eredményről: „Az alapvető részecskék viselkedéséről szerzett ismereteket alkalmazva teljesen váratlanul tiszta matematikai eredményt ért el. Ez csak akkor igaz, ha a dimenziók száma négy.” A matematikus elméleti matematikai munkája rávilágított, hogy a kozmológusoknak és fizikusoknak miért volt annyi bajuk a kozmológiai állandóval és más problémákkal: a négydimenziós geometria viselkedése „deviáns” - és ez csak a négyre igaz. Mi viszont arra vagyunk kárhoztatva, hogy négydimenziós világegyetemben éljünk, legalábbis a fizika szempontjából.
A kozmológusokat nem rettentették el az új felfedezések, sőt új lehetőségeket láttak bennük, és azonnal munkához láttak. Megpróbálták a négydimenziós terekkel kapcsolatos új eredményeket összefésülni saját relativitás- és kvantumelméleti elgondolásaikkal. A cél túlmutatott a kozmológiai állandó nyakon csípésénél, ennél magasztosabb volt, egy valóságos fizikusálom: az egyesített térelmélet megalkotása, amely leírja az összes természeti erőt. A kozmológusok Einsteint követve jutottak el idáig, aki, miután 1932-ben kivándorolt az Egyesült Államokba, és csatlakozott a Felsőfokú Tudományok Intézetéhez (Institute of Advanced Studies), életének utolsó éveit a fizika különböző területeinek egyesítésével töltötte.
Albert Einstein tudásszomja olthatatlan volt. Hívő emberként a tudományt úgy tekintette, mint az isteni teremtés megismerési folyamatát. A mai tudósok nagy része is így van ezzel. Ők vezetik a kutatásokat, és próbálják megérteni a teremtett világ rejtélyeit. Mélyfilozófiai kérdéseket tesznek fel a világegyetem származásával, jövőjével és természetével kapcsolatban.
1997-ben Stephen Hawking azt nyilatkozta, hogy húsz éven belül kezünkben lesznek a világegyetem alapvető törvényei. Más kozmológusok ezt azonnal cáfolták, mondván, hogy húsz éve is ezt mondta volna. De Hawking úgy viselkedett, mint aki még tartogat egy-két ütőkártyát. Einstein szellemében így folytatta: „Közelítünk Istenhez.”66 1998 márciusában Hawking előhúzott egy adut. Az „instanton” fogalmával próbálta az ősrobbanást megmagyarázni. Hawking és munkatársai szerint ez a fogalom közelebb vitte a tudományt a „minden elméletéhez”. Egy hónappal később az éppen Kaliforniában tartózkodó Hawking és kollégája, a londoni Neil Turok nagy hírverés közepette bejelentették az új elmélet világra jöttét. De Hawking nem Einstein, forduljon bár Istenhez, ahogyan ő tette volna. Hawking és csapata mind a mai napig nem álltak elő semmivel, ami csak megközelítette volna Einstein elméletét.
Mit is értek el eddig? Hawking és Turok Alan Guth felfúvódó modelljéből indult ki. Sejtve azt, amit az 1998-as felfedezések megerősítettek, tehát hogy a világegyetem „nyílt”, és ezért be fogja tölteni a végtelen űrt korlátlan tágulása során, a következő kérdést tették fel: A felfúvódási elmélet világegyetemének mindenképpen laposnak kell lennie? Az elmélet hívei ugyanis általában ezt vallják, de nem lehet-e mégis nyílt? Hawking és munkatársa, James Hartle néhány éve már próbálkoztak ezzel a megközelítéssel, de a felfúvódó modellt akkor egy zárt világegyetemre próbálták alkalmazni Richard Feynman legendás amerikai fizikus útintegrál-elvét alkalmazva.
Turok, aki nem hitt a lapos és a zárt világegyetemekben, 1995-ben egy előadást tartott Cambridge-ben a nyílt világegyetemmel kapcsolatos kutatási eredményekről. Steven Hawking felfigyelt rá, és ettől fogva együtt dolgoztak. Sokáig próbálkoztak a nyílt világegyetem olyan megközelítésével, ahogyan azt Hartle és Hawking a zárt világegyetemmel tette, de próbálkozásaik kudarcba fulladtak. A problémát a végtelen jelentette. Ha az egyenletben feltűnik egy végtelen összetevő, akkor a Feynman-féle útintegrál-elv nem alkalmazható. Egy szép napon Turok éppen egy matematikai kifejezést írt Hawking táblájára. Hirtelen Hawking megszólította számítógépén keresztül (Hawking egyetlen ujja kivételével teljesen mozgásképtelen, de ez elég neki az egér mozgatásához, és a számítógép hangját használja beszéd helyett). Turok ugyanis véletlenül kihagyott egy fontos tényezőt az egyenletből. Tovább dolgoztak a javított egyenleten, és a végtelen összetevő kiesett. Hirtelen egy olyan tér bontakozott ki előttük, amely felfúvódással írta le a világegyetem fejlődését az ősrobbanástól egy nyílt világegyetemig - és a kezdetén nem volt szingularitás.
A szingularitás helyett Turok és Hawking bevezették az instanton fogalmát. Ez egy roppantul tömör téridőrészecske, tömege borsónyi, de mérete a borsóénak csak a milliomod trilliomodának a trilliomoda. Azért választották ezt az elnevezést, mert létezése csupán egyetlen pillanatra (= instant) korlátozódik. Az instanton előtt nem volt tér vagy idő. Az ősrobbanás szingularitásától eltérően az instanton sima. Robbanásakor megkezdődik az Alan Guth által feltételezett kozmikus felfúvódás. Az instantonból keletkezett világegyetem pedig végtelenül terjed tovább. Lehet, hogy az elkövetkező évek világűr-megfigyelési eredményei alapján eldől majd, hogy melyik elmélet a helyes, hogy hogyan kezdődött a világegyetem, hogy vajon egységesíthetőek-e a természeti erők, és hogy a kozmológiai állandó vajon része-e az egész fizikát átfogó egyenletnek.
A legtöbb tudós egyetért abban, hogy a világegyetem valószínűleg egy hatalmas tágulás során keletkezett egy nagyon forró, sűrű állapotból, valamiféle ősrobbanással. Ez a hihetetlen erejű kezdeti tágulás indította el az anyag, az energia, majd később a galaxisok: csillagok és bolygók kialakulását, valamint ekkor jött létre a titokzatos, láthatatlan sötét anyag. De arról, hogy hogyan folytatódott a történet az ősrobbanás után, a legkülönbözőbb nézetek, sőt filozófiai irányzatok születtek. Saul Perlmutter, aki a világ legerősebb távcsövének segítségével eddig a legközelebb jutott ahhoz, hogy gyakorlatban is megfigyelje a világegyetem tágulását, óvatos. Eredményei alapján neki is megvan a saját elmélete.
Saul Perlmutter 1959-ben született az illinoisi Urbana-Champaignban. Mindkét szülője akadémikus, fiuk születésekor az állami egyetemen dolgoztak. Saul még kisfiú volt, amikor Philadephiába költöztek, ahol kvéker iskolába járt. A
matematikával és a természettudományokkal nem volt sok gondja, ezért idejét inkább a humán tanulmányokra fordította, hiszen ez jelentett nagyobb kihívást. Hegedült is. A Harvardon tanult tovább; 1981-ben filozófiai és fizikai diplomát szerzett, majd a berkeleyi Kaliforniai Egyetemen folytatta tanulmányait a fizikai doktori cím elérése érdekében. Itt az évek folyamán több nagy teljesítményű kutatócsoport munkáját is megismerte. 1982-ben egy törtnagyságú részecskéket kutató csoporttal dolgozott, de hamarosan inkább azokhoz a végzett hallgatókhoz csatlakozott, akiket Richard Muller professzor vezetett. Muller maga Louis Alvareznek, a néhai szabadgondolkodó fizikusnak a tanítványa volt, aki Walter nevű fiával megtalálta annak bizonyítékát, hogy a 65 millió éve élt dinoszauruszok kihalását egy nagy aszteroidabecsapódás okozta.
Muller és tanítványai továbbvitték elképzelésüket: a halványvörös csillagok csillagászati megfigyeléseit használták egy Nemezis nevű csillag megtalálására. A Nemezis a Nap feltételezett társcsillaga, amely 52 millió évenként kerüli meg azt. Amikor legközelebb van hozzá, tehát 26 millió évenként, tömeges kipusztulások történnek, mivel a Nemezis gravitációs vonzereje aszteroidákat húz magával, és lódít felénk. Ha valaki megtalálná a Nemezist, az nemcsak a dinoszauruszok kihalásának módját adná meg, hanem ennek, és más hasonló katasztrófáknak az okát is. A csoport a parallaxis módszerével megmérte kb. 300 csillag távolságát. Ezeket 2000 „gyanúsított” közül választották ki egy csillagkatalógusból, de mindegyik túlságosan távolinak bizonyult. A keresést különböző okok miatt felfüggesztették. Saul egy hónapra eltűnt; mint utóbb kiderült, ezt az időt a Berkeley egyik fizikaépületének pincéjében töltötte. Amikor kijött, kezében egy új találmányt tartott: egy robottávcsövet.
Saul az új eszközhöz új célokat keresett. Számítógépes vezérlésű távcsövével egy egészen új eljárással keresett szupernóvákat: a távoli galaxisokat módszeresen végigpásztázta. 1985-re húsz ilyen ritka fajtájú robbanást talált a távolban.
1986-ban megkapta a fizikai tudományok doktora címet, majd a következő évben Carl Pennypacker kollégájával együtt rájöttek, hogy a robottávcsöves technika nem csak a szupernóvák felkutatására alkalmas, de segítségével meg lehetne mérni a világegyetem lassulásának mértékét. Tudnunk kell, hogy még 1987-ben is az volt az uralkodó fizikai nézet, hogy az ősrobbanással kezdődött világegyetemnek lassulnia kell a benne lévő anyagok kölcsönös tömegvonzása miatt. A csoport elkezdte méréseit egy ausztráliai négyméteres távcső segítségével, z = 0,3-nál szupernóva-robbanásokat találtak, de nem haladtak elég gyorsan. Az időjárás gyakran megakadályozta a megfigyelést, és más nehézségek is adódtak. A csapat egyre népesebb lett, ezért megfigyelési központját áttette a Kanári-szigetek La Palma nevű tagjára, ahol egy 2,5 méteres távcsövet használhattak. A tudósok eddigre elérték a z = 0,45-ös értéket, és nagyobb adagokban dolgozták fel az adatokat, vagyis nagyobb galaxismegfigyelési halmazokból választottak ki egyre több szupernóvát. Eredményeiket egyenesen a Berkeleyre küldték az interneten keresztül.
Ekkor Saul már a Berkeley Nemzeti Laboratórium alkalmazásában állt; ez az épület az egyetem dombjai fölött helyezkedik el. A laboratórium lett a megfigyelések központja. Mivel a csapat jó eredményeket ért el, egyre jobb távcsöveket használhattak. Végül már a Föld legjobb távcsövét használták, a hawaii 9,8 méteres Keck-ikertávcsöveket és a Hubble-űrtávcsövet. A távoli robbanásészlelések meghökkentő rendszerességgel történtek. De az összes megfigyelés egy olyan képet rajzolt ki, amely éppen ellenkezett azzal, amit a tudomány akkori állása szerint vártak. A világegyetem tágulása nem. lassul, hanem gyorsul. A különböző vöröseltolódási szinteken folytatott megfigyelések alapján úgy látszott, hogy az ősrobbanás utáni időszaktól körülbelül hétmilliárd évvel ezelőttig a világegyetem valóban egyre lassabban tágult. De a világegyetem anyagainak sűrűsége egyszerűen nem volt elegendő a tágulás leállításához. A világegyetem növekedett, anyaga ritkult, és felülkerekedett Einstein „fura energiája”. Hétmilliárd évvel ezelőtt ismét felgyorsult a tágulás, és a világegyetem most is egyre gyorsabban növekszik.
Perlmutter kísérleti tudós, ezért mindig kész adatai átértelmezésére. Alapelve, hogy minden felmerülő feltételezés minden lehetséges ágát végig kell járni. 1999 tavaszára azonban már annyi, egy irányba mutató mérési eredménnyel rendelkeztek, hogy nem volt kétséges: a világegyetem egyre gyorsabban tágul. Perlmutter a megfigyelések alapján most úgy gondolja, a világegyetem lapos, vagyis euklideszi geometriájú, és tágulása korlátlan. A kutatás végén a csillagászok már az eredetileg tervezettnél sokkal távolabbi galaxisokból gyűjtötték adataikat. Olyan távoli galaxisokból (z = 1,2), amelyekből a fény akkor indult el a Földre, amikor a világegyetem tágulása még lassult. Ez ellentétes az adatok nagy többségével, hiszen a z = 0,7 távolságra lévő galaxisok a jelenlegi, gyorsulva táguló világegyetemről tanúskodnak. Azért is mentek távolabbra, hogy kipróbálják, elméletük milyen határok között igaz. Eddig minden adat alátámasztotta feltételezésüket.
A csoport eredményei alapján Perlmutter azt is állítja, hogy a kozmológiai állandónak fontos szerepe van, és éppen hogy nem Einstein legnagyobb baklövése, hanem igenis elengedhetetlen része a világegyetemet, annak múltját és jövőjét meghatározó egyenletnek. Perlmutter, a legtöbb mai csillagászhoz hasonlóan, hisz a felfúvódó világegyetem elméletében. Ezek szerint - és a legújabb csillagászati kutatások alapján levont, széles körben elfogadott következtetések is ezt támasztják alá -világegyetemünk egy hatalmas tágulással kezdődött, ami évmilliókon keresztül lassult, majd újra gyorsulni kezdett - és ma itt tartunk. Ha a következtetések valóban helyesek, a világegyetem tágulása soha nem ér véget.
- Nem tudhatjuk pontosan, mi is történhetett akkor - az ősrobbanás egyedülálló jelenség. Nem hiszek a titokzatos, soha nem látott mezőkben és gyermek- vagy szülő-világegyetemekben. Semmi nem támasztja alá ezeket a feltételezéseket - mondta nekem Sir Roger Penrose. Ő 1965-ben állt elő saját elméletével, amelyben hatékony topológiai módszerekkel bizonyította a téridő ősrobbanáskori szingularitását. - Azt hiszem, a világegyetem geometriája hiperbolikus, de ehhez nem kell kozmológiai állandó, nem hiszek benne. Kétségeim vannak a felfúvódó világegyetem elméletével kapcsolatban is. Nem szeretem, amikor valaki kitalál egy elméletet, és ha a kísérleti adatok nem támogatják, egyszerűen megváltoztatja, újra és újra.
Alan Guth véleménye más: - Még nem tudjuk pontosan, hogy a felfúvódás hogyan történt, de majdnem biztos vagyok, hogy a világegyetem csak így kezdődhetett. Ez az egyetlen meggyőző magyarázat arra, hogyan lett a világegyetem ilyen nagy, egyenletes és lapos. A tudósok kétségtelenül addig fognak vitázni, amíg meg nem fejtik a világegyetem rejtélyét. Egy dologban azonban megegyeznek, és ez nem más, mint Einstein általános relativitáselméletének abszolút ereje és hasznossága. Ha valóban „Isten gondolataira” vagyunk kíváncsiak, valószínűleg kvantumelméleti megfontolásokkal kell kibővítenünk a relativitáselmélet. Akármilyen legyen is a végső egyenlet, Einstein egyenlete biztosan fontos része lesz. Einstein életének álma teljesült fantasztikus egyenletének leírásával - valamennyit biztosan hallott Isten gondolataiból. Álljon itt tehát még egyszer Einstein kozmológiai állandót tartalmazó téregyenlete, amely a mai napig leginkább közelíti Isten egyenletét:
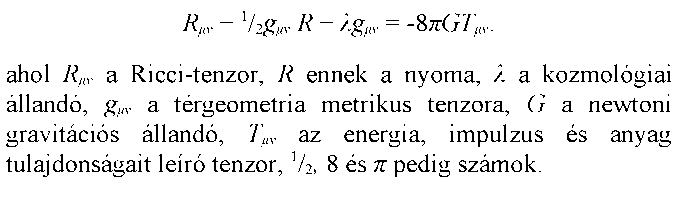
Einstein A későbbi éveim (Out of My Later Years, New York: Philosophical Library 1950, 48. oldal) című könyvében utal arra, hogy hogyan látja a jövőt, és hogy miért nem tudta megalkotni a „minden” egyesített elméletét:
Az általános relativitáselmélet még nem teljes, hiszen a relativitás általános elvét kielégítően csak gravitációs terekre tudja alkalmazni, az egész térre nem. Még nem tudjuk bizonyosan, hogy milyen matematikai eszközzel írható le az egész tér, és milyen nagyobb, változatlan törvényeknek engedelmeskedik. Egy dolog azonban biztosnak tűnik: az általános relativitáselmélet biztosan szükséges és hatékony eszköze lesz az egész tér problémája megoldásának.
Einstein tudta, hogy törekvéseit a matematikai eszközök hiánya akadályozza. A speciális relativitáselmélet kidolgozásakor Lorentz és Minkowski matematikáját használta, az általános relativitáselmélethez pedig először Ricci és Levi-Civitá, később pedig Riemann matematikáját. De itt meg kellett állnia. Közel járt Isten egyenletének kiderítéséhez, de a továbblépéshez új matematikai eszközök kellettek volna. Olyanok például, amilyenekre S. S. Chern utalt princetoni beszédében: magasabb szintű geometriai és topológiai absztrakciók. A matematikusok előbb-utóbb majd kidolgozzák ezeket, a fizikusok alkalmazzák őket, a csillagászok megerősítik, és adataikkal alátámasztják azokat, a kozmológusok pedig megrajzolják világegyetemünk képét.
Amikor majd minden egyes tudományág támogatja a többi fejlődését, megérthetjük talán a természeti törvényeket, és leírhatunk talán egy egyenletet, amely majd megközelíti -amennyire ez az embertől lehetséges - Isten egyenletét. Az egyenlettel a kezünkben meg tudjuk majd oldani a teremtés csodálatos rejtélyét. Lehet, hogy Isten éppen ezért küldött ide minket?