АКАДЕМИЯ НАУК СССР

Научно-популярная серия

Я. Е. ГЕГУЗИН

 

питается из одного источника — умения смотреть, ви­деть и удивляться. И кто знает, сколько еще будет увидено и понято благодаря капле?

Недавно встретилась мне великолепная книга о спеле­ологах — людях, изучающих пещеры, подземные каналы и коридоры, размытые миллиардами капель. Ее авторы, исходившие сотни подземных троп и тропок, назвали книгу «Вслед за каплей воды»...

А вот что написано о капле в «Толковом словаре» Да­ля. Слова «капля» нет, есть «капать», а «капля» — в качестве одного из множества производных слов. Они в словаре занимают места больше, чем находящиеся поблизости «капелла», «капитан», «капкан», «капрал» и «каприз», вместе взятые. «Капля» обросла множеством сентенций. Кто-то глубокомысленно заметил, что «океан начинается с капли», а кто-то — что «капля воды обладает всеми свой­ствами воды, но бури в ней заметить нельзя».

Много лет мечтал я написать книжку очерков о капле. Снимал кинофильмы, запоминал встречавшиеся стихи, в которых были строки о капле, сохранял короткие записи об историях, связанных с каплей. Готовился к книге, но не писал, что-то сковывало меня. И вот недавно встре­тилась мысль, которая придала мне решимость. Мысль о том, что писать книгу надо хотя бы для того, чтобы ос­вободиться от иллюзии, что можешь написать ее.

Итак, книжка очерков о капле. Не «Сталагмологии», а книжка очерков.

 

 

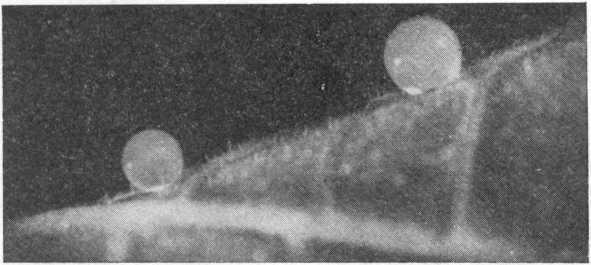
опыта,— что форма капли может оказаться близкой к сферической и в том случае, если она не находится в не­весомости. Для этого капля должна быть настолько мала, чтобы ее вес не мог заметно исказить сферическую форму, которую ей стремится придать поверхностное натяжение. Попытаемся определить, какую каплю в этом смысле сле­дует считать «маленькой». Для этого надо сравнить два давления: то, которое придает капле форму сферы, и то, которое ее расплющивает. В случае «маленькой» капли второе давление должно быть значительно меньше первого.

   

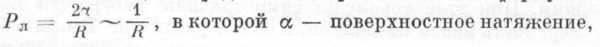
давления, равного отношению силы тяжести капли, масса которой т, к площади контакта между каплей и твердой поверхностью, точно определить трудно, потому что неизвестна величина этой площади. Его можно оценить, посчитав, что площадь контакта приблизительно равна квадрату радиуса капли.

В этом предположении

 

Все рассуждения о почти сферической форме «малень­кой» капли могут совершенно потерять смысл, если силы поверхностного натяжения на границе капля — твердая 

 

разования формы капли в сферическую капля оторвется от твердой пластинки, на которой она лежит? Решить такую задачу просто. Это могут сделать восьмиклассники в на­чале учебного года, узнав, что кинетическая энергия тела равна половине произведения его массы на квадрат скоро-

 

 

Фильм о слиянии двух капель

 

 

 

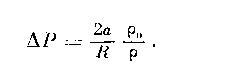
того, чтобы получить участок изогнутой поверхности, ограничивающей жидкость.

Вспомним о капле — она вся ограничена изогнутой по­верхностью, и значит, давление пара вблизи нее будет повышено на величину, определяемую формулой Кельви­на: чем меньше радиус капли, тем большее давление пара над ней. В этом легко убедиться с помощью многих опытов — далее мы с ними еще встретимся, а здесь, вместе с Эйн­штейном, восхитимся талантом Кельвина — его проница­тельным умом и великолепной логикой.

Много лет подряд вместе с моим покойным учителем Бори­сом Яковлевичем Пинесом мы занимались изучением по­ристых кристаллических тел. Так случилось, что я ни разу не спросил, как у него возникло представление о капле пустоты — поре в кристалле. А сейчас, к сожа­лению, спросить уже некого и остается лишь стро­ить догадки, сопоставляя факты и отрывки случайных раз­говоров.

Образ капли пустоты прочно вошел в физику твердого тела, о нем вспоминают всякий раз, когда надо осмыс­лить поведение различных дефектов в кристалле. И я расскажу о том, как этот образ возник. На примере рож­дения образа капли пустоты можно проследить, как вя­жется логическое кружево мысли ученого, где сосущест­вуют и конкурируют фантазия и строгая формальная ло­гика.

Борис Яковлевич не очень был склонен к аналогиям, упрощенным моделям, картинам, иллюстрирующим мысль. Он часто повторял, что картина — образование дву­мерное и, следовательно, неглубокое. Аналогия может появиться позже, а вначале должна быть формула, числен­ная оценка. И еще, посмеиваясь, он любил говорить о том, что иных формулы гипнотизируют, поскольку формула — это математика, а математика, как известно, наука точ­ная. Это преувеличенное почтение к формулам обычно испытывают люди, которые никогда не создавали их и поэтому не чувствуют ни их слабостей, ни таящихся в них возможностей.

 

 

 

 

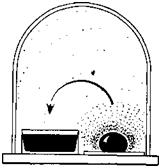
ской поверхностью воды в блюдце. Через некоторое время капли исчезнут — они испарятся, а возникшие при этом в водяном паре молекулы воды сконденсируются на по­верхности воды в блюдце.

Итак, в начале опыта под колпаком было три объекта: вода в блюдце, вода в каплях и насыщенный водяной пар. Опыт окончился, когда один из объектов исчез — капель не стало. Здесь все ясно: согласно формуле, давление пара над изогнутой поверхностью водяной капли больше, чем над плоской поверхностью воды в блюдце, и пар под влиянием этой разности давлений двигался по направлению к блюд­цу — уходил оттуда, где его давление больше, и приходил туда, где его давление меньше. Чтобы вблизи своей поверх­ности поддерживать давление, предписываемое ей форму­лой, капля должна все время испаряться. Она это добро­совестно делала и в конце концов исчезла.

А теперь тот же опыт только не с каплями и атомами ре­альной жидкости, а с «каплями» и «атомами» пустоты. Вме­сто колпака с блюдцем и каплей — монокристалл. Он огра­нен плоскими поверхностями и в объеме имеет одну пору сферической формы. Вблизи изогнутой поверхности поры (капля!) концентрация вакансий повышена, а вблизи плоской поверхности, которая отделяет кристалл от ок­ружающего пространства (вода в блюдце!), концентрация вакансий нормальная, не повышена. Очевидно, появится поток вакансий от поры к поверхности кристалла, и, подобно капле воды, пора исчезнет — «испарится в кри­сталл». Образовавшийся при этом в кристалле избыток вакансий со временем сгладится — вакансии либо по­глотятся внутренними стоками, либо с помощью диффузии переместятся к внешней поверхности кристалла.

Начали мы опыт с пористым, а окончили с беспористым кристаллом! Как быстро это произойдет? Все зависит от размеров поры и температуры кристалла. Например, пора, радиус которой один микрон, в медном кристалле при тем­пературе 1000° С исчезает приблизительно за 30 мин.

Все рассказанное о формуле, об аналогии между реаль­ными каплями и каплями пустоты лежит в основе целого раздела современной физики твердого тела— физики спе­кания, которая объясняет, как пористые кристаллические тела самопроизвольно при высоких температурах превра­щаются в плотные. Оказывается, капли пустоты могут испаряться в кристалл!

 

 

му, чтобы давление, обусловленное изогнутой поверхностью жидкий свинец — воздух, было в точности равно тому давлению, которое обусловлено искривленностью поверх­ности жидкий свинец — твердое железо, т. е. дна ямки.

Равенство двух этих давлений означает, что    . Итак, давления равны, а кривизна двух поверхностей различна, потому что различны соответствующие поверхностные энер­гии.

 

Выкопав под собой ямку, капля как бы перенеслась в невесомость — как и в невесомости, капиллярное давление оказалось одинаковым вдоль всей поверхности, огра­ничивающей каплю.

Естественно возникает вопрос: каким образом капля вы­копала ямку? Ответим на него. Вначале, когда капля была расположена на плоской поверхности железа, она прижи­малась к нему тем давлением, которое обусловлено искрив­ленностью поверхности свинец — воздух. Под влиянием этого давления железо из-под свинцовой капли перемещалось в области вокруг нее. Перемещалось в процессе диф­фузии поатомно, атом за атомом — опыт ставился при высокой температуре, когда диффузия в железе происхо­дит достаточно активно.

Надо подчеркнуть, что в описанном опыте капиллярное давление, которое обусловливает перемещение железа из-под свинцовой капли, существенно больше давления, обусловленного ее весом, так как капля свинца была очень «маленькая» в том смысле, в каком мы об этом гово­рили в очерке об опыте Плато.

Итак, в названии очерка все точно. Попав на твердую поверхность, капля действительно готовит себе удобную постель: либо изгибает подложку, если ей это удается, либо выкапывает для себя удобную ямку.

Раздавленная капля

Аналогия рождается на перекрестках памяти и раздумий и иногда связывает воедино образы и события, состоящие в очень дальнем родстве. Неожиданная аналогия, даже от­даленная или поверхностная, родившись вовремя, может помочь исследователю выйти из тупика и осветить путь к решению.

Когда-то, в конце 40-х годов, я участвовал в экспери­ментальной работе. Ее цель заключалась в определении физических характеристик вещества, которое ранее не исследовалось. Ранее этого вещества в чистом виде просто не было — ценой больших усилий его получили химики.

На первый взгляд задача совсем не новая, и решать ее следует, двигаясь путями, проторенными многими исследо­вателями, изучавшими физические характеристики других веществ. Наша задача, однако, была усложнена тем, что экспериментировать мы могли лишь с микроскопическими крупинками. Каждая крупинка весила около одной мил­лионной грамма, а размер ее — несколько десятков мик­рон. Количеством крупинок мы были очень ограничены — химики их добывали с трудом.

Группа, в которой я работал, должна была определить температуру плавления и поверхностное натяжение веще­ства в жидкой фазе.

 В обычном «макроскопическом» эксперименте температу­ра плавления измеряется легко и просто: в образец по­гружают термометр и следят за тем, как меняются его показания по мере нагрева образца. Температура посте­пенно возрастает. Когда она достигнет некоторого значе­ния, ее рост приостановится в связи с тем, что тепло, при­текающее к образцу, начнет расходоваться не на нагрев, а на процесс расплавления. Эта температура и является тем­пературой плавления. Когда же масса крупинки — одна миллионная грамма, термометр внедрить в нее невозмож­но и для определения температуры плавления следует ис­кать обходные пути.

Один из участников нашей группы, у которого за пле­чами были годы работы в литейном цехе, предложил совсем неожиданное решение задачи. Его память храни­ла воспоминание, родившее аналогию. В годы войны, ска­зал он, я вел плавку одновременно в нескольких одина­ковых тигельных электропечах. Загружал их алюмини­евыми чушками и, чтобы определить начало расплавления шихты в печи, не забираясь на ее загрузочную площадку, в каждую печь между чушками вертикально устанавливал длинный металлический стержень, который был виден над печью. В момент начала плавления стержень наклонялся — это служило сигналом.

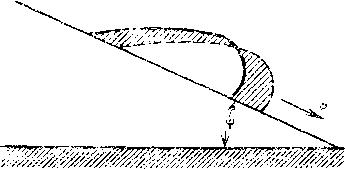
Это воспоминание подсказало идею, с помощью которой можно было измерить температуру плавления крупинки. Опыт заключался в следующем. На тщательно отполиро­ванной пластинке кварца располагалась крупинка. Свер­ху ее накрывали другой пластинкой кварца, которая, ка­саясь крупинки, образовывала некоторый угол с первой пластинкой. Это устройство нагревали, и в тот момент, когда крупинка расплавлялась, верхняя пластинка раз­давливала образовавшуюся каплю и угол между пластин­ками скачкообразно уменьшался. Чтобы надежнее этот момент зарегистрировать, на внешнюю поверхность верх^ ней пластинки нанесли зеркальное покрытие и следили за тем, как отражаемый от нее луч скачком смещается. Пластинка, меняющая свое положение, была подобна ме­таллическому стержню, который наклонялся, свидетель­ствуя о начале процесса плавления. Так как масса кру­пинки пренебрежимо мала по сравнению с массой квар­цевых пластинок, между которыми она зажата, температу­ра крупинки равна температуре пластинок и, следова­тельно, измерить ее весьма просто.

В описанном опыте, вопреки известной пословице, нам удалось убить двух зайцев: определить, во-первых, тем­пературу плавления и, во-вторых, величину поверхност­ного натяжения расплавленного вещества. Дело в том, что верхняя пластинка, раздавливая своей тяжестью кап­лю, превращала ее в лепешку определенной толщины. Сколько раз ни повторялся бы опыт по расплавлению од­ной и той же крупинки, образовывавшаяся жидкая капля весом пластинки расплющивалась до одной и той же тол­щины Эту величину можно было уменьшить, увеличивая вес верхней пластинки. Легко понять, что дальнейшему

расплющиванию препятствуют силы поверхностного на­тяжения, приложенные к той части поверхности расплю­щенной капли, которая граничит с воздухом. В наших опытах вещество капли практически не смачивало кварц (именно поэтому опыты и ставились с кварцевыми пластин­ками) и, следовательно, можно считать, что радиус за­кругления свободной поверхности = /2

Величина поверхностного натяжения может быть опре­делена из условия равенства давления, которое оказывает пластинка на жидкую каплю и лапласовского давле­ния которое обусловлено искривленностью ее свобод­ной поверхности. Если вес пластинки давит на каплю с силой а площадь ее контакта с расплющенной каплей , то = . Величина =       Приравнивая к , находим формулу, с помощью которой можно опреде­лить величину поверхностного натяжения вещества:

           

Величины и можно измерить с большой точностью, а силу легко определить, зная вес верхней пластинки.

Способ решения стоящей перед нами задачи, который подсказала возникшая вдруг аналогия, конечно же, был не единственно возможным. Видимо, можно было приду­мать и иные приемы, но нас привлекла в нем неожидан­ность аналогии и возможность опровергнуть пословицу о двух зайцах.

Что там творится в мире заоконном?

Зима в исходе, видно по всему.

Давайте вместе слушать, как со звоном

Летит сосулька из зимы в весну.

Расскажу об одном очень простом опыте, который когда- то в нашей лаборатории был поставлен и заснят на кино­пленку. «Героем» фильма, естественно, была капля.

Начну с предыстории, с «общих соображений». Во мно­гих учебниках физики утверждается, что жидкость сма­чивает твердое тело того же вещества: жидкая медь — твер­дую медь, вода — лед. Это означает, что если бы, например, на поверхности твердой меди поместить каплю жидкой меди, она должна была бы растечься по ней тонким слоем. Утверждается, что это веществу «выгодно», поскольку при этом его поверхностная энергия уменьшается, т. е. что поверхностная энергия твердой меди на границе с парами меди больше, чем сумма энергий на границе твердая медь — жидкая медь и жидкая медь — пары меди. Разумеет­ся, медь — это лишь пример. Имеется в виду, что утверж­дение справедливо применительно ко многим веществам.

Если авторы учебников физики не заблуждаются, то смачивание твердого тела жидким должно проявлять себя во многих явлениях. Ведь это означает выгодность наличия жидкой пленки на поверхности твердого тела. Чуть курьезно об этом можно сказать так: твердым те­лам выгодно быть мокрыми. Но окружающие нас твердые предметы сухи, если, разумеется, мы их специально не смочим. Впрочем, и смочить их не просто, так как смачи­вать надо жидкостью того же вещества, что и твердое тело, а такая жидкая пленка на твердом теле быстро кристал­лизуется и, присоединившись к нему, становится твердой.

Впрочем, быть может, авторы учебников не заблуж­даются и существуют условия, при которых потребность твердых тел быть мокрыми удовлетворяется. Ведь жидкая пленка на твердой поверхности — это как бы палка о двух концах. С одной стороны, пленка выгодна, так как с ее присутствием связано уменьшение поверхностной энергии,— об этом уже говорилось. С другой стороны, плен­ка невыгодна — с ней связана избыточная «объемная» энергия: если пленка закристаллизуется, выделится энер­гия, и тем большая, чем дальше отстоит температура, при которой находится твердое тело, от температуры его плавления. Если дело обстоит так, то, быть может, авторы учебников все же правы и их правота не противоречит нашему жизненному опыту, протестующему против того, что якобы все твердые тела должны быть мокрыми. Быть может, твердые тела станут мокрыми, когда их температура непосредственно приблизится к температуре плавления, когда проигрыш «объемной» энергии будет меньшим, чем выигрыш «поверхностной». Ведь процессы, которые в природе происходят самопроизвольно, всегда движимы стремлением к уменьшению энергии. Скажем так: камень сам в гору не покатится, а вот с горы — при первой воз­можности.

В первые послевоенные годы в одном из томов «Докладов АН СССР» было опубликовано описание интересного опы­та, который поставили В. И. Данилов и Д. С. Каменецкая. Опыт заключался в следующем. Маленький шарик ме­таллического натрия, состоящий из нескольких кристал­ликов, медленно нагревался в ультратермостате, где тем­пература поддерживалась и регулировалась с большой точ­ностью, кажется, не меньшей пяти тысячных градуса. Гра­ницы между отдельными зернами на поверхности шарика очерчивались канавками. Они образовывали узор, по­добный тому, который образуют швы на покрышке фут­больного мяча. Канавки на шарике сохранялись при всех температурах, однако, когда до температуры плавления оставалось менее одной сотой градуса, они исчезли и вся поверхность шарика, ранее бывшая матовой, как бы покрывалась глазурью. Когда шарик натрия немного охлаждался, канавки снова появлялись, а затем повтор­ным нагревом можно было заставить их исчезнуть, а по­верхность покрыться глазурью. Это наблюдение очень .естественно объясняется «общими соображениями»: жид­кость смачивает собственное твердое тело, и поэтому вбли­зи температуры плавления твердое тело должно покрыться жидкой пленкой — это она сглаживает канавки и придает поверхности блеск глазури.

Авторы опыта с шариком натрия изучали не причины и закономерности появления и исчезновения канавок на его поверхности. Это наблюдение — побочный результат опы­та, и поэтому они специально не стремились убедиться в том, что вблизи температуры плавления натрий запотевает, покрывается тонким жидким слоем.

Опыт, о котором рассказано, очень красив, но его ре­зультат лишь косвенно свидетельствует о правильно­сти утверждения, что жидкость смачивает твердое тело того же вещества. Если жидкая пленка появляется — ка­навки должны исчезнуть, но не исключено, что они исче­зают по каким-либо иным причинам, а причин может быть множество.

Здесь можно оставить предысторию и «общие соображе­ния» и перейти к опыту, о котором говорилось в начале очерка. Мы пытались придумать прямой опыт, результат которого, не допуская кривотолков, убедил бы нас в том, что твердое тело с готовностью покроется жидкостью того же вещества, если такая возможность будет ему предостав­лена. Вспомнили о ментоле — веществе, расплав которого очень легко переохлаждается. Кристаллики ментола пла­вятся при 35° С, но и при комнатной температуре ментол может оставаться жидким.

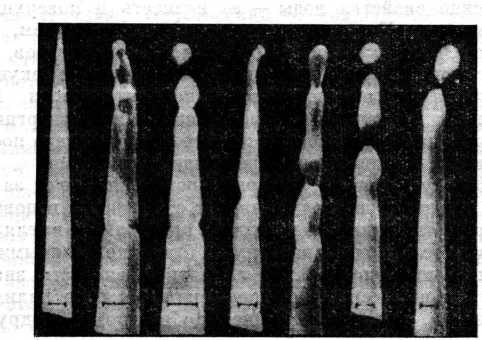
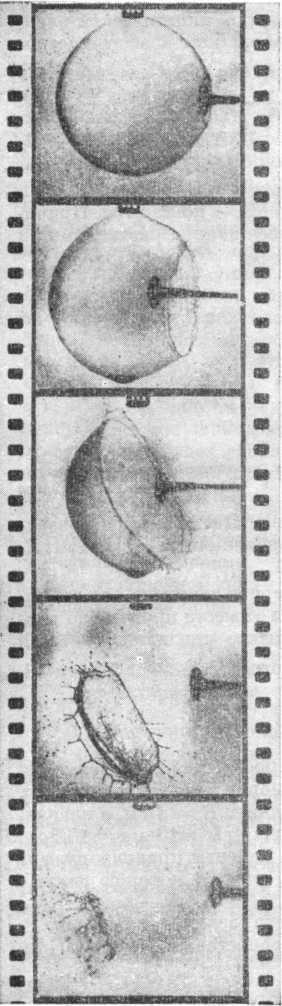
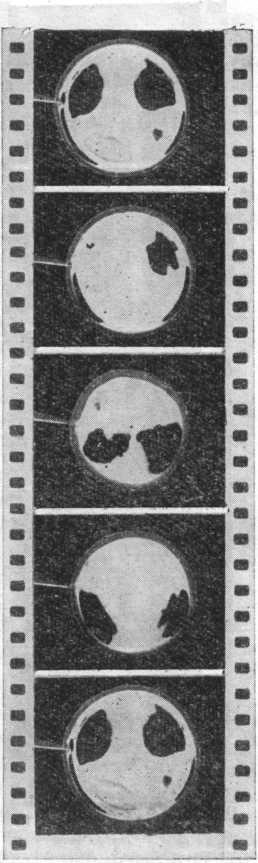
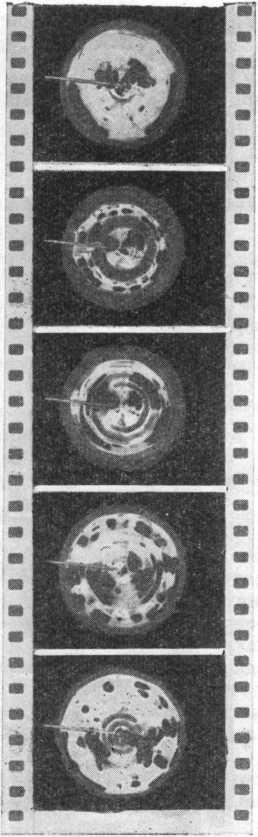
Опыт заключался в следующем. На стеклянной пластин­ке поместили маленький кристалл ментола, подогрели его, расплавили, и он превратился в жидкую каплю. Менто­ловая капля немного растеклась по стеклу и приняла форму плоской лепешки. Затем взяли ментоловую иголоч­ку — продолговатый кристаллик ментола, сечение кото­рого было много меньше площади капли,— и опустили ее в ментоловую переохлажденную жидкую каплю.

Рассуждали так. Игла из кристаллика ментола может вмешаться в судьбу капли двумя различными способами. Она может явиться затравкой, которая вызовет кристал­лизацию переохлажденной ментоловой капли. В этом слу­чае капля, затвердев, останется на стекле в виде твердой лепешки, которая по форме мало отличается от формы жид­кой капли. Может произойти и иное: ментоловая игла, ока­завшись в непосредственном контакте с жидким ментолом, начнет жадно втягивать его на свои свободные поверхности, чтобы закрыть их жидкой пленкой. Если это произойдет, игла осушит каплю, как бы промокнет ее.

Произошло именно это: у места контакта с каплей игла начала утолщаться. Дело об­стояло так. Жидкий ментол, который в виде тонкого слоя наполз на поверхность иглы, кристаллизовался. На воз­никшую при этом свежую твердую поверхность опять наползал ментол и в свою очередь тоже кристаллизо­вался. Так происходило до тех пор, пока вся масса жид­кой капли не перебралась на иглу. Разумеется, процессы наползания и кристаллиза­ции не следовали один за другим, а происходили одно­временно, но наползание бы­ло ведущим процессом.

 

Нам, конечно, повезло — могла бы осуществиться пер­вая возможность, и капля осталась бы на стекле твер­дой лепешкой. В чем же при­чина везения? Главным обра­зом в том, что наползал мен­тол на иглу со скоростью большей, чем кристаллизо­вался. Опыт с иным вещест­вом, которое, как и ментол, подчиняется правилу, описан­ному в учебнике физики, окончился бы неудачей, если бы соотношение между скоро­стью наползания и кристал­лизации было неблагоприят­ным для проявления напол­зания и капля отвердела бы прежде, чем заметная ее часть успела бы наползти на иглу.

Обнаружив, что игла мо­жет осушить каплю, мы реши­ли заснять этот процесс на киноленту и теперь показываем студентам двухминутный фильм на лекции, посвящен­ной явлениям на границе между твердой и жидкой фазами. Кинограмма, иллюстрирующая очерк, смонтирована из кадров этого фильма.

Талая вода

Весеннюю капель, таяние снега, ручейки талой воды я по­чему-то всегда встречаю с грустью. Приход весны вызы­вает у меня ощущение не начала чего-то, а конца... Все свои планы я строю не на «учебный год» и не от новогод­ней ночи и до новогодней ночи, а от талой воды и до талой воды. Гонг, отбивающий годы, в моих ушах звучит весен­ней капелью.

Каждую весну я с грустью гляжу на талую воду. Много весен мелькало, но никогда я не задумывался над тем, как снег — белый и пушистый — рождает талую воду? Вопрос этот не возникал, видимо, потому, что ответ предполагал­ся простым и давно известным: снег состоит из снежинок — кристалликов, эти кристаллики, как и все кристалли­ческие тела, при определенной температуре плавятся, пре­вращаясь в жидкость. Для снега эта «определенная тем­пература» — нуль градусов. Вот и все.

Мне «по долгу службы» следовало бы больше знать об особенностях плавления снега. Снег ведь это не просто со­вокупность отдельных снежинок, каждая из которых ве­дет себя независимо. В снеге снежинки соприкасаются, об­разуя ажурную конструкцию из кристаллов и пустоты, а это, быть может, как-то влияет на судьбу отдельной сне­жинки? Быть может, капля воды рождается снегом не так, как снежинкой? Следовало бы знать, но я этого не знал, и лишь благодаря случаю пристальнее пригляделся к то­му, как рождается талая вода — капля за каплей.

Я жил зимой в лесу, в небольшом деревянном домике. В отличие от сказочных лесных избушек, забытых богом и людьми, этот домик людьми не был забыт. Люди, персонал Дома отдыха, домик утеплили, установили в нем много батарей парового отопления и гнали по ним столько горячего пара, что в комнате было нестерпимо жарко. Темпера­тура воды в графине достигала, кажется, 30° С. Пить эту воду было неприятно, и я решил приготовить холодную воду — растопить снег и напиться талой воды. Вокруг домика было много свежего, сверкающего снега. 

Здесь начинается рассказ о физическом опыте. Назовем его так: опыт первый. Про­зрачный стеклянный стакан я доверху заполнил снегом, немного притрамбовал его и поставил в комнате на столе. Со временем снег опустился ниже кромки стакана и отстал от стекла. Минут через пят­надцать объем снега умень­шился почти вдвое. Снег те­рял белизну, в нем явно об­разовывалась вода, но на дне стакана ее не было — ни кап­ли! Первые капли талой воды появились позже, когда снег, промокнув, начал в стакане расползаться, оседать.

Этот случайно поставлен­ный опыт убедительно свидетельствовал о том, что, пла­вясь, снег удерживает в себе воду. Или лучше так: ту воду, которая раньше всего обра­зуется на поверхности снега, где температура наиболее вы­сока, снег всасывает в себя. Это удивительно напоминает осушение ментоловой капли ментоловой иглой. Вместо ментоловой иглы — пористый снег, в котором много поверх­ностей, «жаждущих» покрыть­ся водой, вместо жидкого ментола — вода, образующая­ся при плавлении поверхност­ного слоя снега.

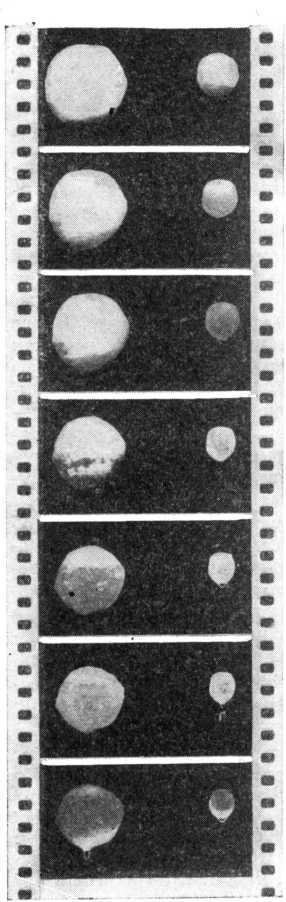
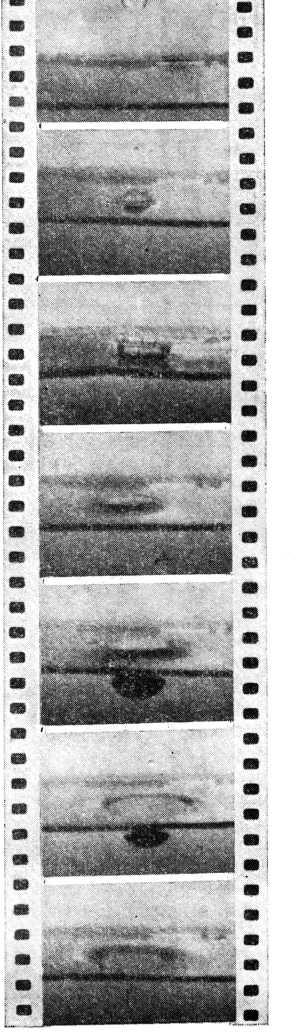
Первый случайный опыт мне показался нечистым, «упрекаемым», так как не все участки поверхности снега стакане были в одинаковых условиях: боковая поверхность и верхний торец снежного цилиндра соприкасались с воздухом, а нижний торец, на котором цилиндрик стоял,— со стеклом стакана. Я поста­вил опыт преднамеренно — опыт второй. Из снега слепил небольшой шарик — такой, каким ребята играют в снеж­ки. Продел сквозь него нитку и наблюдал за тем, что про­исходит со снежной сферой, прежде чем от нее отделится первая капля талой воды.

Позже, уже в условиях лаборатории, этот опыт был пов­торен аккуратнее, со многими снежными сферами разных размеров, и все увиденное заснято кинокамерой. Чтобы результаты опытов можно было обработать количественно, рядом с шарами расположили масштабную линейку и ча­сы. Кинолента рассказала о том, что со временем при ком­натной температуре все снежные шары уменьшаются. Внизу каждого из них появляется вода, которая, однако, не капает, а остается в снегу. Снежная сфера со всех сто­рон равномерно обогревается воздухом, и вода появляется на всей ее поверхности. Капиллярными силами она втя­гивается в объем сферы, а затем под действием силы тяже­сти собирается в ее нижней части. Здесь сфера темнеет. Накапливающаяся вода продвигается к «макушке» сферы, и, когда весь объем сферы «напьется», от нее отделится пер­вая капля. А затем капля за каплей — весь снег истечет талой водой. Чем меньше сфера, тем раньше появится пер­вая капля.

Немного простых рассуждений. Очевидно, перед рожде­нием первой капли, насытившись водой, т. е. заполнив ею все поры, снежная сфера уменьшит свой объем на величи­ну, равную объему пор. Объем пор равен произведению на­чального объема сферы на одинаковую для всех сфер величину пористости. Именно поэтому относительное изменение объема сферы до момента рождения первой капли не должно зависеть от ее начального размера. Ведь именно эта величина равна пористости. Из опы­тов и следовало, что относительное изменение объема снежной сферы не зависит от ее начального радиуса.

А теперь — немного стихов. Как-то мне попались на глаза такие строки о таянии снега:

...Что зима с землей ни делала,

Как ни била, как пи жгла —

Из-под снега, из-под белого

Снова речка потекла... 

Стихи эти очень складные, но очень неточно отражают процесс таяния: «из-под снега, из-под белого» талая вода не течет. А вот строки из стихотворения Николая Забо­лоцкого «Оттепель»:

...Оттепель после метели.

Только утихла пурга,

Разом сугробы осели

И потемнели снега...

Из-под такого снега талая вода вскоре появится — вначале капля, а затем бурный весенний поток.

Много физических явлений связано с весенней капелью. Например, можно рассказать о закономерностях образования изумительной по совершенству и красоте «каплевидной» формы капли, готовящейся оторваться от тающей сосульки. Не могу объяснить почему, но форма набухающей капли мне представляется верхом гео­метрического совершенства. Разве лишь сфера может сравниться с ней по красоте и логической законченнос­ти формы. Можно рассказать о солнечных бликах, жи­вущих на поверхности капли, которая набухает на кончи­ке сосульки. Блики колеблются в ритме дыхания набухающей капли. Можно рассказать о весеннем звоне, который, по мысли поэта, сопровождает полет сосульки из зимы в весну. Звон капели звучит во многих стихотворных и музыкальных строчках, и, ко­нечно же, следовало бы рассказать об акустике удара капли о поверхность воды или льда, покрытого водяным слоем. Капля разбивается на мелкие осколки, и каж­дый из осколков вносит свое звучание в весенний звон.

Много физических явлений связано с весенней капелью, а здесь рассказ лишь об одном из них — о том, что проис­ходит в тот момент, когда набухшая капля отрывается от родившей ее сосульки. Обычно глаз этого явления не замечает, точнее — в глаза оно не бросается. А кинокаме­ра помогла сделать его зримым, очевидным.

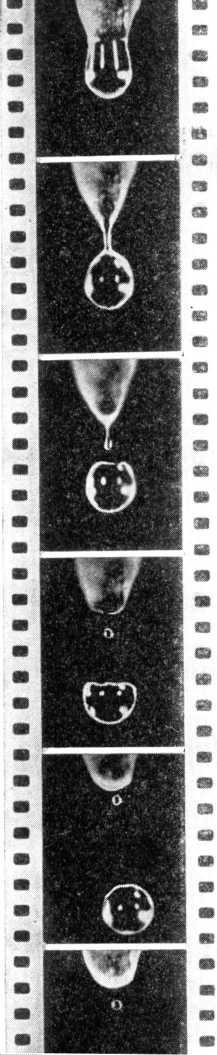
Перед нами две кинограммы, смонтированные из кад­ров ленты, на которую был заснят процесс отрыва капли от двух различных сосулек, одна из которых — поострее, а другая — потупее. Первые кадры на этих кинограммах практически одинаковы. Они рассказывают о том, что на­бухающая капля увеличивает свой объем и, двигаясь по направлению к земле, вытя­гивает тонкую перемычку — связующее звено между со­сулькой и каплей. Затем капля от перемычки отрыва­ется и свободно падает, а оставшаяся перемычка начи­нает изменять свою форму. Она укорачивается, утолща­ется в нижней части и в виде сформировавшейся капельки отрывается от сосульки. Итак, рождению каждой крупной капли сопутствует рождение еще одной малень­кой капельки. Ее объем суще­ственно, приблизительно в 100 раз, меньше объема пер­вой капли, и, как правило, глаз ее не замечает.

Судьба маленькой капли оказывается очень неожидан­ной. Возникнув,она не летит вслед за падающей большой, а, наоборот, начинает дви­гаться вверх, по направле­нию к сосульке. Иногда это движение оканчивается тем, что малая капля достигает сосульки и как бы поглоща­ется ею, а иной раз, немного переместившись вверх, она летит вниз вслед за большой.

Судьба маленькой капли зависит от того, какой тол­щины была перемычка, пре­вратившаяся в капельку, а толщина перемычки зависит от того, насколько остра таю­щая сосулька. Капельки, воз­вращающиеся в сосульку, обычно рождаются сосулька­ми остроконечными. Кинограммы потому и различают­ся последними кадрами, что они относятся к сосулькам с разным углом при вершине.

Попытаемся понять то, о чем рассказывают кинограм­мы. После отрыва большой капли с перемычкой происхо­дят два процесса: первый — на ее конце формируется маленькая капелька; вто­рой — капиллярными силами эта капелька подталкивается вверх. Эти силы не возникли бы, если бы капля была обо­собленной, ограниченной сфе­рической поверхностью. В та­кой капле было бы лишь скомпенсированное давление всестороннего сжатия. Кап­ля на кончике сосульки ввер­ху не закрывается сфериче­ской поверхностью, и поэтому к противоположному участку ее поверхности приложена нескомпенсированная сила, обусловленная лапласовским давлением она-то и тол­кает каплю вверх.

 

В тот мо­мент, когда маленькая кап­ля, сформировавшись, отрывается от сосульки, она еще продолжает двигаться вверх. Достигнет или не достигнет она сосульки, зависит от ее массы, от соотношения между силой, толкнувшей каплю вверх (), и силой тяжести (), но некоторое движение вверх, как правило, наблю­дается всегда.

 

Точно, с помощью формул, описать все происходящее с маленькой каплей очень не просто. Ограничимся прибли­женной оценкой. Сила, вы­нуждающая капельку падать вниз, определяется точно:

А вот силу, толкающую каплю вверх , можно лишь грубо оценить, придав определенное значение диаметру перемыч­ки, соединяющей капельку с сосулькой. Если — радиус капли, — радиус перемычки, а   = ,  то   =

Чтобы капелька на­чала двигаться вверх,необхо­димо выполнение условия Из этого условия следует, что <   

Предположим, что 10. Разу­меется, не точно 10, но тако­го порядка. В этом случае 

 

Капля падает на жидкость

представлялась лилия, а другому — гвоздик c алмазною шляпкой

 

  

  

 

 

 

  

 

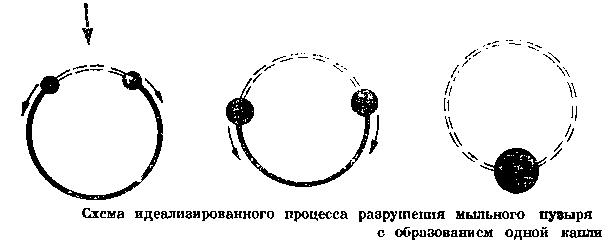
все тело пленки (пузыря) свернется в одну каплю радиусом

, найдем скорость, с которой движется валик от точки прокола к точке, диа­метрально противоположной которой и возникнет капля. Для упрощения расчета предположим, что пленка плоская. Учет ее изогнутости усложнил бы расчет и лишь немного уточнил результат. Исчезновение части пленки приво­дит к освобождению поверхностной энергии, кото­рая, будем считать, превращается в кинетическую энергию движущегося валика. К тому моменту, когда образуется отверстие, радиус которого

 

 

 

 

 

 

 

 

, которое проходит между двумя приседаниями. Его можно определить, рас­суждая следующим образом. Растущая со временем капля будет увеличивать свой раз­мер до тех пор, пока давле­ние, оказываемое ею на струю (

 

показывает, что . Удобнее эту формулу перепи­сать в виде:

 

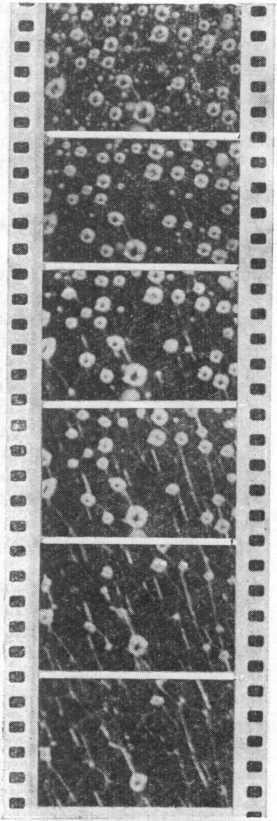
Последняя формула естественно объясняет понижение точки, в которой начинается распад капель, с ростом на­пряженности

Получается своеобразный высо

 

 

 

К. Паустовский

—

 

 

 

— 

 

  

 

 

 

 

 

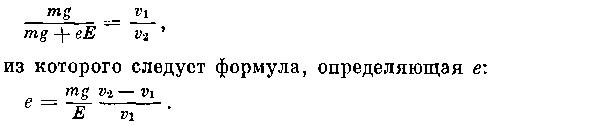
Алексей Толстой

 

 

 

   

 

 

 

  

 

 

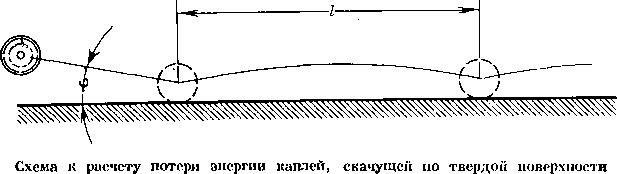
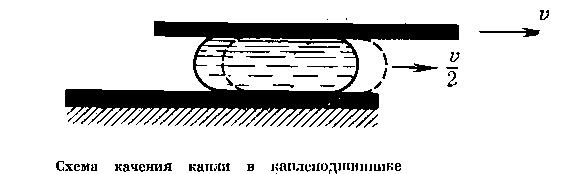
Естественно, может возникнуть следующая мысль: быть может, не следует мудрить с каплеподшипниками, а про