
Вселенная полна удивительных тайн. Возможно, она скрывает от нас дополнительные измерения, разительно отличающиеся от всего, что может себе представить наш здравый смысл, взращенный в обычном трехмерном пространстве. И хотя с каждым годом мы узнаем все больше и больше о нашем мире, сегодня как никогда ранее мы осознаем, что для понимания истинной природы Вселенной нам необходимо сделать еще очень многое.
Лиза Рэндалл принадлежит к разряду тех ученых, которые сами, своими собственными исследованиями совершают прорывы и раздвигают границы современной науки, пытаясь найти ответы на фундаментальные вопросы, поставленные природой.
Л. Рэндалл проводит нас через потрясающий мир закрученных дополнительных измерений, лежащих, возможно, в основе нашей Вселенной, и показывает путь, следуя которому мы сможем убедиться в их существовании.
Книга «Закрученные пассажи» увлекает читателя в удивительное путешествие, проводя его через цепочку открытий от начала двадцатого века до настоящих дней, объясняя суть противоречий между теорией относительности, квантовой механикой и гравитацией, описывая достижения физики элементарных частиц, проблему иерархии, скейлинг, Великое объединение, суперсимметрию, дополнительные измерения, параллельные миры, эволюцию струнных теорий и многое другое.
В непринужденной и занимательной форме Лиза Рэндалл беседует с читателем, раскрывая таинства сложной науки и увлекательно объясняя загадки мириад миров, существующих, возможно, рядом с тем миром, в котором мы живем и который мы только начинаем постигать.
Книга вызовет несомненный интерес как у специалистов естественно-научных дисциплин, так и у широкого круга читателей.
Лиза Рэндалл
Закрученные пассажи: Проникая в тайны скрытых размерностей пространства
Лиза "Рэндалл, без сомнения, является одним из ведущих, физиков-теоретиков в области космологии…
Дух захватывает от мысли, что всего в нескольких сантиметрах от нашей Вселенной может существовать другая вселенная, оставаясь для нас совершенно недоступной, ибо эти несколько сантиметров отмерены в четвертом измерении, в то время как мы находимся в плену у наших трех измерений!
Сэр Мартин Рис, член Королевского общества, профессор Кингс-колледжа
Книга «Закрученные пассажи» логично объясняет новые интригующие идеи, необходимые сегодня физикам для того, чтобы изучать природу физической реальности. От читателя не требуется специальных знаний, только любознательность и живой интерес к науке. Лиза Рэндалл ведет нас от простых интуитивных представлений к более сложным понятиям современной физики, и далее — к самым захватывающим рубежам науки.
Стивен Линкер, автор книг «Язык как инстинкт» и «Субстанция мышления»
Книга Лизы Рэндалл — это ослепительный фонтан новых понятий… которые, без сомнения, расширят кругозор и обогатят научный лексикон любого, кто прочтет эту книгу. И что удивительно — самые фантастические идеи новой физики, похоже, гармоничны с миром, каков он есть.
Адам Гопник, автор книг «Париж — Луна» и «Король в окне»
Увлекательный и поразительно ясный рассказ о том, как наличие дополнительных измерений, помимо привычных нам трех (или четырех, если учитывать время), может разрешить множество космологических загадок.
New York Times Book Review
Предисловие научного редактора
Книга Лизы Рэндалл «Закрученные пассажи», русский перевод которой предлагается вниманию читателей, посвящена изложению на общедоступном уровне важнейших результатов, полученных в последнее десятилетие в области моделей взаимодействий элементарных частиц в пространстве-времени с дополнительными измерениями. Автор книги является известным специалистом по физике элементарных частиц и по теориям с дополнительными измерениями пространства-времени и внесла значительный вклад в развитие таких моделей.
Следует заметить, что гипотеза о существовании дополнительных измерений пространства-времени обсуждается в теоретической физике уже около ста лет и за это время претерпела значительные изменения. Тот факт, что в окружающем нас макроскопическом мире дополнительные измерения пространства не наблюдаются, обязательно должен иметь объяснение в теориях, основанных на этой гипотезе. В первоначальном варианте этого подхода — в теориях Калуцы — Клейна, названных так по фамилиям их создателей, — ненаблюдаемость дополнительных измерений пространства в нашем макроскопическом мире объяснялась их очень малым, порядка длины Планка, размером. Длина Планка равна 10-33 см, что примерно в сто миллионов миллиардов (1017) раз меньше тех расстояний, которые доступны для наблюдения на самых мощных современных ускорителях частиц. Вследствие этого оказывается, что экспериментально наблюдать проявление дополнительных измерений пространства в этом случае невозможно.
Около тридцати лет назад в работах советских ученых В. А. Рубакова и М. Е. Шапошникова для теорий с дополнительными измерениями был предложен новый сценарий, основанный на идее локализации частиц, из которых состоит наш мир, в тонкой области вблизи трехмерной поверхности в многомерном пространстве с дополнительными измерениями. Такие области в физике называются доменными стенками, и на них может возникать потенциальная яма для материи, из которой состоит наш мир. Этот сценарий допускает существование больших и даже бесконечных дополнительных измерений, не наблюдаемых при доступных в настоящее время относительно низких энергиях. Однако при более высоких энергиях дополнительные измерения могут оказывать влияние на физические процессы в нашем мире и, таким образом, стать наблюдаемыми.
Если нас не интересует конкретный механизм удержания частиц на доменной стенке и последнюю можно считать бесконечно тонкой, то возникает новый физический объект — мембрана, или просто брана, т. е. трехмерная поверхность в многомерном пространстве, на которой локализована материя, из которой состоит наш мир. Модели такого типа получили название моделей мира на бране, и оказалось, что они возникают также в теории суперструн.
Мировую известность Лизе Рэндалл принесла опубликованная в 1999 г. совместно с Р. Сундрумом работа, в которой была сформулирована первая последовательная модель мира на бране, получившая название модели Рэндалл — Сундрума. Этот материал входит в число наиболее цитируемых работ во всех областях науки. Главная цель, поставленная автором данной книги, — донести до читателя новейшие идеи о дополнительных измерениях пространства, обсуждаемые в современной теоретической физике, объяснить на качественном уровне, без привлечения сложного математического аппарата, как эволюционировали представления о пространстве-времени. Эти идеи неразрывно связаны с физикой элементарных частиц и с космологией и, как полагают работающие в этих областях ученые, позволяют объяснить многие загадки микро- и макромира.
Физику элементарных частиц также невозможно представить себе без квантовой механики и специальной теории относительности. Поэтому обсуждению этой теории и возможной роли в ней дополнительных измерений предпослан достаточно подробный обзор достижений физики XX века, который отражает оригинальный взгляд автора на развитие этой науки и может представлять самостоятельный интерес для читателей.
В начале книги обсуждаются специальная и общая теории относительности Эйнштейна, квантовая механика, Стандартная модель взаимодействий элементарных частиц и ее симметрии. Затем автор рассматривает теории за рамками Стандартной модели: суперсимметрию, теории струн и бран.
Последующие главы, посвященные обсуждению дополнительных измерений пространства-времени и их роли в физике элементарных частиц и в космологии, в значительной степени основаны на результатах исследований автора книги. В них не только изложены доступным языком последние достижения в этой области, но и интересно и эмоционально рассказано о самом процессе получения результатов.
Книга написана ярким, образным языком. Для объяснения сложных физических понятий в ней используются совершенно неожиданные аналогии из повседневной жизни.
Через всю книгу проходит забавное сказочное повествование, перекликающееся с «Алисой в стране чудес», отдельные истории которого предваряют каждую главу и метафорически аннотируют ее содержание.
Английский язык оригинала весьма своеобразен, поэтому перевод этой книги был сопряжен со значительными трудностями. Переводчик А. В. Берков и редакторы перевода постарались найти максимально близкие русские эквиваленты, чтобы передать это своеобразие и донести до читателя мысли и эмоциональный настрой автора. Насколько это удалось — судить читателю.
При чтении книги может сложиться впечатление, что все достижения в этой области науки принадлежат Западу, а вклад советских и российских ученых совсем невелик. В действительности это далеко не так, просто так сложилось, что в западной научной литературе работы советских и российских ученых зачастую замалчиваются при цитировании. Как уже говорилось выше, сама идея о возможности существования макроскопически ненаблюдаемых больших дополнительных измерений впервые была высказана советскими учеными, в книге же об этом говорится вскользь, без упоминания имен. Аналогично суперсимметрия впервые была найдена советскими физиками Ю. А. Гольфандом и Е. П. Лихтманом, в книге же эти имена упоминаются вместе с группой западных ученых, впоследствии развивавших эту теорию.
Российские физики также внесли значительный вклад в исследование модели Рэндалл — Сундрума. В частности, в работах [Рубаков В. А. Большие и бесконечные дополнительные измерения. Введение // ЖЭТФ. 2001; Боос Э.Э., Волобуев И. П., Михайлов Ю. А., Смоляков М. Н. Эффективные лагранжианы модели Рэндалл — Сундрума // ТМФ. 2001] было показано, что при последовательной интерпретации этой модели более естественным является рассмотрение дополнительного измерения размером порядка 10-17 см, а не планковского размера 10-33 см, как в оригинальной работе. Возможно, выбор создателями модели планковского размера дополнительного измерения объясняется их неосознанным желанием установить соответствие с теорией суперструн.
Книга Л. Рэндалл, несомненно, представляет собой заметное явление в научно-популярной литературе. Она дает возможность неподготовленному читателю ощутить всю красоту и сложность современной теоретической физики, познакомиться с ее новейшими достижениями и понять трудность стоящих перед ней проблем.
И. П. Волобуев, доктор физико-математических наук
Предисловие и благодарности
Когда я была маленькой девочкой, я обожала игры и интеллектуальные головоломки, находя их в задачниках по математике или в книгах типа «Алисы в стране чудес». Однако, хотя чтение было одним из моих любимых занятий, научные книги меня особо не привлекали, ибо казались довольно отстраненными — я не чувствовала себя достаточно увлеченной и не ощущала вызов. Стиль часто казался снисходительным, слишком превозносящим ученых, а иногда просто скучным. Я чувствовала, что авторы окружают ореолом тайны результаты или превозносят тех людей, которые их получили, вместо того чтобы описывать саму науку и тот процесс, посредством которого ученые устанавливают взаимосвязь между явлениями. А мне хотелось знать именно это.
Чем больше я интересовалась наукой, тем сильнее она меня увлекала. Я еще не знала, что стану физиком; никто из тех, с кем я была знакома в юности, наукой не занимался. Но занятия неизведанным непреодолимо манили меня. Мне казалось восхитительным искать связи между кажущимися совершенно различными явлениями, решать проблемы и предсказывать удивительные свойства нашего мира. Сейчас, став физиком, я понимаю, что наука является живой сущностью, которая находится в постоянном развитии. Ее делают интересной не только ответы, но также вопросы, дух соперничества и само участие.
Когда я задумала написать эту книгу, мне представлялось, что она должна передавать восторг, который я чувствую от моей работы, не ущемляя научную точность изложения. Я надеялась передать очарование теоретической физики, не прибегая к обманчивому упрощению предмета или представлению его в виде конечного набора застывших монументов, которыми следует покорно восхищаться. Физика намного созидательнее и интереснее, чем это многим кажется. Я хотела поделиться этими чувствами с людьми, которым, возможно, не довелось самостоятельно дойти до такого понимания.
Новая картина мира довлеет над нами. Дополнительные измерения изменили представления физиков о Вселенной. И поскольку связи этих измерений с нашим миром могут оказать влияние на множество хорошо установленных физических законов, дополнительные измерения предлагают новые захватывающие подходы к объяснению старых, уже проверенных фактов о Вселенной.
Некоторые идеи, включенные мной в книгу, довольно абстрактны и умозрительны, однако нет причин полагать, что любознательный читатель не сможет их понять. Я решила дать возможность физике говорить самой за себя и не стала делать акцент на истории и отдельных личностях. Мне не хотелось создавать ошибочное впечатление, что все физики устроены одинаково или что физика интересна какому-то конкретному типу личности. Опираясь на свой опыт и беседы с людьми, я убедилась в том, что есть много читателей, которые сообразительны, любознательны и достаточно открыты к восприятию новой информации, чтобы заинтересоваться реальным положением дел.
Эта книга не обходит вниманием ни одну из самых продвинутых и заманчивых теоретических идей, но я постаралась сделать все возможное, чтобы изложение было замкнутым. Я включила как ключевые концептуальные идеи, так и физические явления, к которым они применяются. Главы построены так, чтобы читатели могли продвигаться по книге в соответствии со своими знаниями и интересами. Чтобы помочь этому процессу, я выделила в конце глав те моменты, на которые я буду ссылаться позже при изложении новейших идей о дополнительных измерениях. Я также использовала маркеры в конце глав, посвященных дополнительным измерениям, чтобы пояснить, чем отличаются друг от друга разные варианты вселенных с дополнительными измерениями.
Так как идея о дополнительных измерениях, вероятно, нова для многих из читателей, в первых главах я объяснила, что я понимаю под этими словами, и почему дополнительные измерения могут существовать, но при этом быть невидимыми и неосязаемыми. После этого я обрисовала теоретические методы, которые используют специалисты в области физики элементарных частиц, для того чтобы объяснить тип мышления, характерный для таких весьма умозрительных исследований.
Современные работы по дополнительным измерениям опираются как на традиционные, так и на современные понятия теоретической физики для обоснования исследуемых вопросов и используемых в них методов. Чтобы объяснить, что движет такими исследованиями, я включила обширный обзор физики двадцатого века. Можно пролистать этот обзор «по диагонали». Но, поступив так, вы пропустите много интересного.
Обзор начинается с общей теории относительности и квантовой механики, и лишь после этого мы переходим к физике частиц и ее важнейшим понятиям. Я изложила довольно абстрактные идеи, которыми часто пренебрегают отчасти именно из-за их абстрактности, но все теоретические представления, о которых я говорю, на данный момент экспериментально подтверждены и используются во всех современных исследованиях. Хотя не весь материал существен для понимания в дальнейшем идей, касающихся дополнительных измерений, я думаю, что многие читатели будут рады получить более полную картину.
Затем я описала ряд новых, более умозрительных теоретических схем, изучавшихся в последние тридцать лет, в частности суперсимметрию и теорию струн. Традиционно физика предполагает взаимодействие теории и эксперимента. Суперсимметрия — это расширение известных понятий физики частиц, и есть хорошие шансы на то, что она будет проверена в предстоящих экспериментах. Теория струн иная. Она основана исключительно на теоретических представлениях и идеях и даже до сих пор не полностью сформулирована математически, так что мы не можем быть абсолютно уверены в ее предсказаниях. Что касается меня, то я в этом вопросе являюсь агностиком — я не знаю, как в конечном итоге будет выглядеть теория струн и сможет ли она разрешить проблемы квантовой механики и гравитации, на которые она нацелена. Но теория струн была богатым источником новых идей, некоторые из которых я сама использовала в исследованиях по дополнительным измерениям пространства. Эти идеи существуют независимо от теории струн, однако данная теория дает основания считать, что некоторые из лежащих в их основе предположений могут быть верными.
Совершив эту экскурсию и обрисовав ситуацию, я снова вернусь к описанию современных исследований по дополнительным измерениям. Они приводят нас к удивительным заключениям, например, к тому, что дополнительные измерения могут быть бесконечными по размеру, оставаясь при этом невидимыми, или что мы можем жить в трехмерном пространственном колодце в многомерной Вселенной. Теперь мы знаем причины того, что могут существовать невидимые параллельные миры со свойствами, сильно отличающимися от свойств нашей Вселенной.
На протяжении всей книги я объясняю физические теории, не прибегая к уравнениям. Однако для тех читателей, которых интересуют детали, я включила математическое приложение. В основном тексте я попыталась расширить диапазон метафор, используемых для объяснения научных понятий. Значительная часть нашего обычного словарного запаса оперирует пространственными аналогиям, однако эти аналогии часто не годятся для микроскопического мира элементарных частиц и трудно представимого пространства с дополнительными измерениями. Мне казалось, что менее привычные метафоры, например, из области искусства, пищи и личных отношений, могут работать по меньшей мере не хуже при объяснении абстрактных идей.
Чтобы подготовить читателя к восприятию новых идей, я начинаю каждую главу с кратенькой истории, вводящей ключевое понятие с помощью более знакомых метафор и представлений. Эти истории меня забавляют, поэтому, если захотите, вернитесь назад, прочтя главу, чтобы уловить суть дела. Эти истории можно рассматривать как двумерный рассказ, идущий «вниз» сквозь главы и «горизонтально» поперек книги. Или вы можете относиться к ним как к забавному заданию, которое позволяет вам проверить, насколько вы усвоили идеи главы.
Многие друзья и коллеги помогали мне достичь поставленных в этой книге целей. Хотя я понимала, к чему стремлюсь, я не всегда сознавала, где добилась успеха. Многие люди заслуживают благодарности за щедрую трату своего времени, поддержку, интерес и любопытство к тому, что я написала.
Некоторые талантливые друзья заслуживают особой благодарности за неоценимые комментарии и замечания в процессе написания книги. Анна Кристина Бюхман, чудесная писательница, сделала прекрасные подробные замечания, которые помогли мне понять, как следует завершать рассказанные мной истории как о физике, так и о жизни. Она давала бесценные советы, всегда приправленные ободрением. Полли Шульман, моя другая невероятно талантливая подруга, внимательно прочла и прокомментировала каждую главу. Я восхищаюсь ее логичным и живым умом, и мне повезло, что она предложила свою помощь. Любош Мотль, блистательный физик, посвятивший себя популяризации науки (специфическое мнение которого о женщинах в науке мы опускаем), прочел все, даже до того, как это стало пригодным для чтения, и сделал на каждой стадии ряд чрезвычайно полезных предложений. Том Левенсон дал важный совет, который может дать только искусный писатель, пишущий о науке, и внес ряд особо значимых предложений. Майкл Гордин посмотрел на книгу с точки зрения историка науки и знатока литературы подобного рода. Джейми Робинс сделала глубокие замечания по нескольким версиям рукописи. Эстер Чиао сделала полезные замечания к рукописи с точки зрения умного, заинтересованного читателя, не имеющего научного образования. Наконец, я рада, что Кормак МакКарти добровольно оказывал ценную помощь и вносил предложения на заключительных стадиях подготовки книги.
Ряд людей поделились со мной интересными историями и наблюдениями, которые помогли мне на начальных стадиях этого проекта. Массимо Поррати является кладезем уникальных фактов, часть из которых приведена в книге.
Взгляды Джералда Холтона на физику начала XX века обогатили мои представления о квантовой механике и теории относительности. Йохен Броке высказал полезные мысли о том, что ему нравится в литературе о науке, и стимулировал ряд литературных идей. Беседы с Крисом Хаскетом и Энди Синглтоном помогли мне понять, что способны воспринять и хотели бы узнать нефизики. Альбион Лоуренс сделал ряд ценных замечаний, позволивших мне сделать более понятными некоторые трудные главы. Наконец, Джон Свейн предложил пару раз, как изящно изложить материал.
Многие коллеги внесли ценные замечания и предложения. Среди тех, кому я благодарна, Боб Кан, Чаба и Сусанна Чаки, Паоло Креминелли, Джошуа Эрлих, Эми Кац и Нейл Вайнер — они прочли основные части книги и сделали ряд глубоких замечаний. Я благодарю также Аллана Адамса, Ниму Аркани-Хаме-да, Мартина Гремма, Джонатана Флинна, Мелиссу Франклин, Дэвида Каплана, Андреаса Карча, Джо Ликкена, Петера Лу, Энн Нельсон, Аманду Пит, Рикардо Раттаци, Дэна Шрага, Ли Смолина и Дариена Вуда за полезные замечания и ценные советы. Говард Джорджи советовал мне и многим упомянутым выше физикам обращаться к языку эффективной теории, который используется в этой книге. Я также признательна Петеру Бохачеку, Венди Чан, Энрике Родригесу, Полу Грему, Виктории Грей, Полу Мурхаузу, Курту МакМаллену, Лиам Мерфи, Джефу Мрагену, Сеше Претап, Дэне Рэндалл, Энрике Родригесу и Юдифь Сур-кис за критику, предложения и поддержку. Я также благодарю Марджори Карон, Тони Карона, Барри Езарского, Джоша Фелдмана, Маршу Розенберг и других членов ее семьи за возможность лучше понять мою аудиторию.
Грег Эллиот и Джонатан Флинн выполнили замечательные рисунки для этой книги, и я им очень признательна. Также благодарю Роба Мейера и Лауру Ван Вик за помощь при получении разрешений на множество содержащихся в книге цитат. Я приложила максимум усилий, чтобы правильно упомянуть источники. Если кому-то покажется, что они не процитированы должным образом, пусть даст мне знать.
Я хочу также поблагодарить моих сотрудников по тем исследованиям, о которых я рассказываю в этой книге, в частности Рамана Сундрума и Андреаса Карча, работа с которыми доставляла мне истинное удовольствие. Кроме того, я хочу отметить вклад многих физиков, размышлявших над подобными и близкими идеями, включая те, про которых мне не хватило места упомянуть.
Выражаю признательность редактору издательства «Экко Пресс» Дэну Галь-перну, моим редакторам из издательства Пингвин Пресс Стефану МакГрату и Уиллу Гудладу и моим литературным редакторам в США и Англии Лайману Лайонсу и Джону Вудрафу за множество полезных предложений и поддержку этой книги. Хочу поблагодарить моего литературного агента Джона Брокмана, а также Катинку Матсон, за их важные комментарии и советы, а также неоценимую помощь в издании этой книги. Я благодарна Гарвардскому университету и Институту высших исследований Радклиффа за предоставленную мне возможность сосредоточиться на работе над книгой, а также МТИ, Принстону, Гарварду, Национальному научному фонду, Департаменту энергии и Фонду им. Альфреда П. Слоана за поддержку моих исследований.
Наконец, я хочу поблагодарить мою семью — родителей Ричарда и Глэдис Рэндалл и сестер Барбару Рэндалл и Дэну Рэндалл — за подпитку моей научной карьеры и за то, что в течение многих лет они разделяли со мной юмор, мысли и воодушевление. Линн Феста, Бет Лайман, Ген Лайман и Джен Сакс оказывали невероятную поддержку, и я благодарю всех их за чудесные советы и предложения. Наконец, я очень благодарна Стюарту Хиллу за глубокие идеи, полезные замечания и бескорыстную помощь. Благодарю вас всех. Надеюсь, вы увидите, что ваши усилия не пропали даром.
Лиза Рэндалл
Кембридж, Массачусетс Апрель 2005
Введение
Got to be good looking
Cause he’s so hard to see.
The Beatles[1]
У Вселенной свои секреты. Одним из них могут считаться дополнительные измерения пространства. Если они существуют, то Вселенная их заботливо скрывает, оградив от людских взоров и спрятав под покрывалом. Размышляя как обыватель, вы никогда о них не догадаетесь.
Кампания по дезинформации начинается с детской кроватки, впервые знакомящей вас с тремя пространственными измерениями. Это два измерения, по которым вы ползаете, и третье, по которому вы карабкаетесь вверх. С этого момента законы физики, не говоря уже о здравом смысле, поддерживают веру в существование трех измерений, подавляя любое подозрение, что их может быть больше.
Однако пространство-время может полностью отличаться от всего, что вы только способны вообразить. Мы не знаем ни одной физической теории, предписывающей наличие только трех пространственных измерений. Отвергнуть возможность дополнительных измерений прежде, чем хотя бы рассмотреть следствия их существования, было бы крайне опрометчиво.

Так же как «вверх — вниз» — это направление, отличающееся от «налево — направо» или «вперед — назад», в нашем космосе могут существовать другие совершенно новые измерения. Хотя мы не можем видеть их своими глазами или ощущать кончиками пальцев, логически дополнительные измерения пространства вполне возможны.
У таких гипотетических невидимых измерений до сих пор нет имени. Но если бы они существовали, они были бы новыми направлениями, вдоль которых что-то могло бы перемещаться. Поэтому, когда мне требуется имя для дополнительного измерения, я иногда называю его проходом или пассажем. (И когда я обсуждаю именно дополнительные измерения, я использую в названиях глав слово «пассажи».)
Эти пассажи могут быть плоскими, как те измерения, к которым мы привыкли. Но они могут быть и искривленными, как отражения в зеркалах комнаты смеха. Они могут быть крохотными, много меньшими, чем размер атома; по крайней мере, именно это предполагали все, кто верил в существование дополнительных измерений. Однако новые исследования показали, что дополнительные измерения могут быть и большими, и даже бесконечно большими по величине, и при этом не поддаваться детектированию. Наши органы чувств говорят нам только о трех больших измерениях, так что бесконечное дополнительное измерение звучит неправдоподобно. Но бесконечное невидимое измерение — лишь одна из многих удивительных возможностей, которые могут реализоваться в космосе. В этой книге мы расскажем, почему это так.
Исследование дополнительных измерений привело также к другим поразительным представлениям, способным удовлетворить фантазии страстного любителя научной фантастики, таким как параллельные вселенные, закрученная геометрия и трехмерные воронки. Боюсь, что подобные идеи больше относятся к сфере деятельности писателей и лунатиков, чем к области реальных научных исследований. Но какими бы диковинными они не казались сейчас, эти идеи являются реальными научными сценариями, которые могут осуществляться в мире дополнительных измерений. (Если вы пока что незнакомы с такими словами или идеями, не тревожьтесь, мы введем и обсудим их позднее.)
Почему нужно рассматривать невидимые измерения?
Даже если физика с дополнительными пространственными измерениями действительно допускает столь невероятные сценарии, вас может все же удивить, почему физики, занятые предсказаниями наблюдаемых явлений, должны беспокоиться и принимать эти сценарии всерьез. Ответ столь же необычен, как и сама идея дополнительных измерений. Согласно недавним исследованиям, дополнительные измерения, до конца еще не изученные и до конца не понятые, могут тем не менее раскрыть ряд первозданных тайн нашей Вселенной. Дополнительные измерения могут быть причастны к видимому нами миру, а идеи относительно этих измерений могут окончательно раскрыть связи, которые ускользают он нас в трехмерном пространстве.
Нам не удастся понять, почему эскимосы внешне похожи на китайцев, если мы не учтем временное измерение, которое позволит установить их общее происхождение. Аналогично, те связи, которые становятся возможными благодаря дополнительным измерениям пространства, могут раскрыть поразительные стороны физики частиц и пролить свет на загадки давностью в несколько десятилетий. Связи между свойствами частиц и взаимодействиями, кажущиеся необъяснимыми, когда пространство заковано в трех измерениях, элегантно совмещаются в мире с большим числом пространственных измерений.
Верю ли я в дополнительные измерения? Признаюсь, да. Было время, когда я проявляла изрядную долю скептицизма, рассматривая физические идеи (включая мои собственные), которые выходили за рамки того, что может быть измерено. Меня привлекали эти идеи, но я честно признавала свое недоверие. Хотя иногда мне казалось, что в этом должен быть какой-то зародыш истины. Однажды, лет пять тому назад, по пути на работу, когда я переезжала реку Чарльз по дороге в Кембридж, я вдруг поняла для себя, что я действительно верю в необходимость существования каких-то форм дополнительных измерений. Я огляделась вокруг и стала всматриваться в многие измерения, которые не могла различить. Это был шок удивления от внезапного изменения моего взгляда на мир, похожий на тот, который я испытала, когда поняла, что я, коренная жительница Нью-Йорка, стала болеть за «Ред Соке» (Red Sox) во время игры на вылет против «Янки» (Yankee) — подобного я никогда не могла себе даже представить[2].

Более близкое знакомство с дополнительными измерениями лишь увеличило мою убежденность в их существовании. Аргументы против них имели слишком много прорех, чтобы заслуживать доверия, а физические теории без них оставляли без ответа слишком много вопросов. Кроме того, исследуя в последние годы дополнительные измерения, мы расширили список возможных вселенных с дополнительными измерениями, которые могут имитировать нашу собственную Вселенную, что наводит на мысль, что мы увидели лишь верхушку айсберга. Даже если дополнительные измерения не точно соответствуют тем картинкам, которые я привожу, полагаю, что они вполне уместны в той или иной форме, а их приложения окажутся неожиданными и поразительными.
Вас может заинтриговать тот факт, что следы дополнительных измерений могут прятаться на вашей кухне, на дне сковородки с антипригарным покрытием из квазикристаллов. Квазикристаллы — восхитительные структуры, лежащий в основе которых порядок раскрывается только с помощью дополнительных измерений. Кристалл представляет собой очень симметричную решетку из атомов и молекул, в которой много раз повторяется один базовый элемент. Известно, какие структуры могут образовывать кристаллы в трех измерениях и какие картины возможны. Однако расположение атомов и молекул в квазикристаллах не соответствует ни одной из этих картин.
Пример квазикристаллической картины показан на рис. 2. В ней нет точной регулярности, встречающейся в настоящем кристалле, картина которого выглядела бы скорее как сетка, нанесенная на лист миллиметровки. Наиболее изящный способ объяснения картин расположения молекул, возникающих в этих странных материалах, использует проекцию — нечто вроде трехмерной тени — кристаллической картины в пространстве с большим числом измерений, которая отражает симметрию картины в многомерном пространстве. В сковородах с антипригарным покрытием, на рабочую поверхность которых нанесены квазикристаллы, используется тот эффект, что проекция многомерных кристаллов на поверхности сковороды имеет структурные отличия от земной структуры обычной трехмерной пищи. Различные расположения атомов, не дающие им связаться друг с другом, являются дразнящим намеком на то, что дополнительные измерения существуют и объясняют ряд наблюдаемых физических явлений.
Обзор
Дополнительные измерения помогают понять необычное расположение молекул в квазикристалле; точно так же в наши дни физики предполагают, что теории с дополнительными измерениями смогут прояснить существующие в физике частиц и космологии связи, которые трудно понять, если ограничиться только тремя измерениями.
В течение тридцати лет ученые опирались на теорию, называемую Стандартной моделью физики частиц, которая рассказывает о фундаментальной природе материи и тех силах, за счет которых взаимодействуют элементарные составляющие [3]. Физики проверили Стандартную модель, воссоздавая частицы, которые существовали в нашем мире только в самые первые секунды жизни Вселенной, и убедились, что Стандартная модель очень хорошо описывает многие их свойства. Однако ряд фундаментальных вопросов остается в рамках Стандартной модели без ответа, и эти вопросы настолько фундаментальны, что их решение обещает новое глубокое проникновение в свойства строительных блоков нашего мира и их взаимодействий.
В этой книге рассказывается о том, как я и другие ученые искали ответы на загадки Стандартной модели и оказались в мирах с дополнительными измерениями. Новые достижения теории дополнительных измерений в конце концов займут в этом рассказе центральное место, но сначала я представлю вспомогательных игроков — революционные достижения физики двадцатого века. Недавние идеи, о которых я позднее расскажу, основаны на этих замечательных прорывах.
Обзорные разделы, с которыми мы познакомимся, можно в общих чертах разделить на три категории: физика начала двадцатого века, физика частиц и теория струн. Мы обсудим ключевые идеи теории относительности и квантовой механики, а также современное состояние физики частиц и проблемы, которые могут быть связаны с дополнительными измерениями. Мы рассмотрим также понятия, лежащие в основе теории струн, которую многие физики считают главным претендентом на роль теории, объединяющей квантовую механику и тяготение. Теория струн, постулирующая, что самыми основными элементами в природе являются не частицы, а фундаментальные колеблющиеся струны, придала значительный импульс изучению дополнительных измерений, так как теория струн требует существования более чем трех пространственных измерений. Кроме того, я опишу роль бран — объектов в теории струн, похожих на мембраны, которые столь же существенны для теории, как сами струны. Мы рассмотрим как успехи этих теорий, так и те вопросы, которые они оставляют открытыми, оправдывая тем самым современные исследования.
Одной из главных загадок является вопрос, почему тяготение настолько слабее всех других известных взаимодействий. Когда вы взбираетесь на гору, вы ощущаете, что тяготение совсем не слабая сила, но это происходит потому, что вас притягивает вся Земля. Маленький магнит может поднять скрепку, даже несмотря на то, что вся масса Земли притягивает ее в противоположном направлении. Почему же тяготение настолько бессильно по сравнению с маленьким усилием крохотного магнита? В стандартной трехмерной физике частиц слабость тяготения представляется большой загадкой. Ответ на нее могут дать дополнительные измерения. В 1998 году мой коллега Раман Сундрум и я нашли одну причину, по которой это может быть так.
Наша гипотеза основана на геометрии закрученного пространства, понятии, возникающем в эйнштейновской общей теории относительности. Согласно этой теории, пространство и время объединены в одну пространственно-временную структуру, искаженную или искривленную материей и энергией. Раман и я применили эту теорию в новом контексте с дополнительными измерениями. Мы обнаружили конфигурацию, в которой пространство-время искажено столь значительно, что даже если гравитация сильна в одной области пространства, она может оказаться ничтожной во всех других областях.
Мы обнаружили еще более поразительную вещь. Для объяснения того, почему не видны дополнительные измерения, физики в течении восьмидесяти лет полагали, что они должны быть крохотными по величине, однако в 1999 году Раман и я обнаружили, что искривленное пространство может объяснить не только слабость гравитации, но и то, что невидимое дополнительное измерение может простираться до бесконечности, если только оно должным образом деформировано в искривленном пространстве. Дополнительное измерение может иметь бесконечный размер, и тем не менее быть скрытым. (Не все физики сразу же приняли нашу гипотезу. Но мои друзья не-физики сразу поняли, что я куда-то продвинулась, и не потому, что они разобрались в науке, а потому, что когда после своего доклада я пришла на банкет конференции, Стивен Хокинг занял мне место.)
Я объясню физические принципы, лежащие в основе этих и других теоретических достижений, и новые представления о пространстве, делающие их допустимыми. Далее мы столкнемся с еще более фантастической возможностью, которую годом позднее обнаружили физик Андреас Карч и я: возможно, мы живем в трехмерном кармане пространства, хотя вся остальная Вселенная ведет себя так, как будто у нее большее число измерений. Этот результат открывает массу новых возможностей для структуры пространства-времени, которое может состоять из отдельных областей, каждая из которых имеет разное число измерений. Мы не только не находимся в центре Вселенной, как пять столетий тому назад сказал Коперник, но, возможно, живем в изолированной области с тремя пространственными измерениями, являющейся частью многомерного космоса.
Изученные в последнее время мембраноподобные объекты, называемые бранами, являются важными компонентами богатых многомерных ландшафтов. Если дополнительные измерения являются игровой площадкой физика, то миры бран — гипотетические вселенные, в которых мы живем на одной из бран, — являются как бы фантастическими многослойными многогранными детскими гимнастическими стенками. Эта книга поведет вас в мир бран и вселенных с закрученными, искривленными, большими и бесконечными измерениями, некоторые из которых содержат единственную брану, а другие состоят из множества бран, приютивших невидимые миры. И все это находится в области возможного.
Возбуждение от неизведанного
Постулированные миры бран являются теоретическим актом веры, а содержащиеся в них идеи — умозрительными. Однако, как при игре на бирже, более рискованные ставки могут привести к проигрышу, но они могут и наградить вас большим выигрышем.
Представьте вид снежного покрова под лыжным подъемником в первый солнечный день после снегопада, когда нетронутый снег манит вас наверх. Вы чувствуете — эх, что бы там ни было, но раз вы встали на лыжи, дальше вас ждет прекрасный день. Некоторые спуски будут крутыми и полными ухабов, некоторые — легкими прогулками, а некоторые — сложными извилистыми путями среди деревьев. Но даже если вы случайно сделаете неправильный поворот, большую часть дня вы будете чудесно вознаграждены.
Для меня построение моделей — под этим физики понимают поиск теорий, которые могли бы объяснять современные наблюдения, — обладает такой же неотразимой привлекательностью. Построение моделей — это путешествие с приключениями сквозь понятия и идеи. Иногда новые идеи очевидны, иногда же найти и использовать их сложно. Однако, даже если мы не знаем, куда они приведут, интересные новые модели часто вторгаются в неизведанные волшебные области.
Сейчас мы не знаем, какая из теорий правильно указывает наше место во Вселенной. Для некоторых теорий мы этого никогда и не узнаем. Но, как это ни кажется невероятным, это не так для теорий с дополнительными измерениями. Самое удивительное свойство любой теории с дополнительными измерениями, объясняющей слабость гравитации, состоит в том, что если она правильна, то мы скоро об этом узнаем. Эксперименты, изучающие взаимодействия частиц очень высоких энергий, могут обнаружить свидетельства в пользу этих предположений и лежащих в их основе дополнительных измерений в течение ближайших пяти лет, как только будет построен и запущен Большой адронный коллайдер (БАК) — ускоритель частиц очень большой энергии вблизи Женевы.
На этом коллайдере, который должен вступить в строй в 2007 году[4], будут изучаться соударения невероятно энергичных частиц, способных затем превращаться в никогда ранее не наблюдавшиеся новые типы материи. Если какие-нибудь из теорий с дополнительными измерениями правильны, они оставят видимые следы на БАК. Свидетельства будут включать частицы, называемые модами Калуцы — Клейна, которые путешествуют в дополнительных измерениях, но оставляют следы своего существования здесь, в знакомых нам трех измерениях. Моды Калуцы — Клейна будут отпечатками пальцев дополнительных измерений в нашем трехмерном мире. А если нам очень повезет, экспериментаторы зарегистрируют и другие улики, возможно, даже многомерные черные дыры.
Детекторы, которые будут фиксировать эти объекты, настолько велики и впечатляющи, что работа на них будет требовать альпинистского снаряжения вроде ремней безопасности и шлемов. Однажды я воспользовалась этим снаряжением, когда взбиралась на ледник в Швейцарии вблизи ЦЕРНа (Европейский центр ядерных исследований), физического центра, в котором находится БАК. Эти громадные детекторы будут регистрировать свойства частиц, которые затем будут использованы физиками для реконструкции соударения.
По общему мнению, свидетельство существования дополнительных измерений будет до некоторой степени косвенным, и нам придется собрать вместе разные улики. Но это верно почти для всех недавних физических открытий. Физика двадцатого века в своем развитии все больше удалялась от вещей, которые можно непосредственно наблюдать невооруженным глазом, к вещам, которые можно «увидеть» только с помощью объединения измерений и теоретической цепочки логических рассуждений. Например, знакомые уже из курса школьной физики кварки, составные части протона и нейтрона, никогда не существуют изолированно; мы находим их, двигаясь по следам, которые они оставляют в результате влияния на другие частицы. Так же обстоят дела с поразительными вещами, известными под названием темная энергия и темная материя. Мы не знаем, откуда взялась большая часть энергии во Вселенной, или какова природа большей части содержащегося во Вселенной вещества. Однако мы знаем, что темная материя и темная энергия во Вселенной существуют, и не потому что мы непосредственно детектировали их, а потому что они оказывают заметное влияние на окружающую их обычную материю. Как кварки или темная энергия и темная материя, существование которых мы устанавливаем лишь косвенно, дополнительные измерения непосредственно не проявляются. Тем не менее следы дополнительных измерений, хотя и косвенные, могут окончательно подтвердить их существование.
Скажем с самого начала, что, очевидно, не все новые идеи оказываются правильными и многие физики скептически относятся к любой новой теории. Не являются исключением и те теории, которые я представляю в этой книге. Однако единственный путь достижения прогресса в нашем понимании — это умозрительное построение. Даже если окажется, что не все детали согласуются с реальностью, новая теоретическая идея может пролить свет на физические принципы, действующие в истинной теории космоса. Я совершенно уверена, что идеи относительно дополнительных измерений, с которыми мы познакомимся в этой книге, содержат значительно больше, чем зачаток истины. Сталкиваясь с неизведанным и работая с умозрительными идеями, я черпаю оптимизм из истории открытий фундаментальных явлений, которые всегда приходили неожиданно и сталкивались со скептицизмом и сопротивлением. Любопытно, что не только простая публика, но иногда те самые люди, которые открывали фундаментальные понятия, поначалу верили в них с большой неохотой.
Например, Джеймс Клерк Максвелл, создавший классическую теорию электричества и магнетизма, не верил в существование фундаментальных единиц заряда, таких как электрон. Джордж Стони, в конце девятнадцатого века предложивший считать заряд электрона фундаментальной единицей заряда, не верил в то, что ученым когда-либо удастся изолировать электроны от атомов, составными частями которых они являются. (На самом деле, все, что требуется, это теплота или электрическое поле.) Дмитрий Менделеев, создатель Периодической системы элементов, отвергал понятие валентности, закодированное в этой системе. Макс Планк, предложивший считать, что свет переносит энергию порциями, не верил в реальность световых квантов, представление о которых неявно содержалось в его собственной идее. Альберт Эйнштейн, который ввел понятие о квантах света, не знал, что их механические свойства позволяют отождествить их с частицами — фотонами, которыми, как мы сейчас знаем, они являются. Однако не каждый, у кого возникали правильные новые идеи, отвергал их связь с реальностью. Многие идеи, несмотря на то, верили в них или нет, оказывались правильными.
Много ли открытий осталось ждать? Для ответа на этот вопрос я обращусь к довольно беспощадным словам Георгия Гамова, выдающегося физика-ядерщика и популяризатора науки. В 1945 году он писал: «Вместо довольно большого числа „неделимых атомов“ классической физики мы имеем теперь всего три существенно различных объекта — нуклоны, электроны и нейтрино…Поэтому похоже, что мы уже достигли дна в нашем поиске базисных элементов, из которых состоит материя». Когда Гамов писал это, он не имел представления о том, что нуклоны состоят из кварков, которые будут открыты через тридцать лет!
Не будет ли странно, если мы окажемся первыми людьми, для которых поиск дальнейшей фундаментальной структуры окажется безуспешным? Настолько странно, что в это на самом деле едва ли можно поверить?
Несогласованности в существующих теориях говорят нам, что они не могут быть последним словом. У предыдущих поколений не было ни инструментов, ни мотиваций современных физиков для исследования арен дополнительных измерений, описанию которых посвящена эта книга. Дополнительные измерения или все, что бы ни лежало в основе Стандартной модели физики частиц, станут открытиями первостепенной важности.
Когда речь идет о мире вокруг нас, есть ли другой выбор, кроме как продолжать изучать его?
I Размерности пространства (и мысли)
Глава 1
Вступительные пассажи: срывая покров тайны с размерностей
You can go your own way.
Go your own way.
Fleetwood Mac[5]
— Икар, я не очень уверена в той истории, которую пишу, я рассматриваю, что будет, если добавить больше измерений. Как тебе эта идея?
— Афина, твой старший брат мало что знает о том, как пишутся истории. Но, бьюсь об заклад, хуже не будет, если добавить новые измерения. Ты собираешься добавить новых действующих лиц, или немного оживить уже имеющихся?
— Ни то, ни другое; я имею в виду совсем иное. Я планирую ввести новые измерения, но только новые измерения в пространстве.
— Ты шутишь, да? Ты собралась писать об альтернативных реальностях, вроде мест, где люди испытывают альтернативный духовный опыт, или мест, в которые они уходят, когда умирают, или переживают предсмертный опыт?[6] Я не думал, что ты докатишься до подобного рода вещей.
— Успокойся, Икар. Ты знаешь, что этого я делать не буду, я говорю о различных пространственных измерениях, а не о различных духовных уровнях.
— Но как могут различные пространственные измерения что-то изменить? В чем разница, буду ли я использовать лист бумаги размерами 27 см х 16 см или 30 см х 22 см?
— Перестань дразниться. Я говорю совершенно не об этом. Я действительно планирую ввести новые измерения пространства, похожие на те, которые мы видим, но направленные в совершенно другие стороны.
— Измерения, которые мы не видим? я думал, что три измерения — это все, что есть.
— Подожди, Икар. Скоро мы все выясним.
Слово «измерение», как многие другие слова, описывающие пространство или движение через него, имеет много интерпретаций, и мне кажется, что на настоящий момент я уже слышала их все. Так как мы видим предметы в пространственной картине, мы пытаемся описать многие понятия, включая время и мысль, в пространственных терминах. Это означает, что многие слова, применяемые для описания пространства, имеют много разных смыслов. И когда мы используем такие слова для технических целей, альтернативное использование слов может привести к тому, что их определения будут звучать странно.
Словосочетание «дополнительные измерения» особенно сбивает с толку, так как, даже если мы применяем эти слова по отношению к пространству, само такое пространство находится вне нашего чувственного опыта. Те вещи, которые трудно зрительно представить, обычно труднее описывать. Просто мы физиологически не созданы для восприятия более чем трех пространственных измерений. Свет, тяготение и все другие средства наблюдения представляют мир, содержащий, по-видимому, только три измерения пространства.
Так как мы не способны непосредственно воспринимать дополнительные измерения, даже если они существуют, многие опасаются, что попытки ухватить их смысл могут привести только к головной боли. По крайней мере, именно это как-то сказал мне журналист Би-би-си во время интервью. Однако спокойствию угрожают не мысли о дополнительных измерениях, а попытка их изобразить. Попытка нарисовать мир с дополнительными измерениями неизбежно приводит к осложнениям.
Размышлять о дополнительных измерениях — это, в общем, совсем другое дело. Мы прекрасно можем представить себе их существование. И когда мои коллеги и я используем слова «измерения» и «дополнительные измерения», в нашей голове есть совершенно точные идеи. Итак, прежде чем сделать следующий шаг вперед или исследовать то, как новые идеи укладываются в нашу картину Вселенной (заметьте, снова пространственные образы), я объясню слова «измерения» и «дополнительные измерения» и то, что я буду иметь в виду, когда буду их далее употреблять.
Вскоре мы убедимся, что когда число измерений больше трех, слова (и уравнения) могут быть ценнее тысяч картин.
Что такое измерения?
Любому из нас каждый день приходится иметь дело с пространствами, имеющими много измерений, хотя скорее всего большинство об этом и не думает. Однако рассмотрим все измерения, которые мы принимаем во внимание, когда решаемся на важный шаг, например, на покупку дома. Вы должны рассмотреть размеры дома, местонахождение школы, близость интересных мест, архитектуру, уровень шума и тому подобное.
Вы должны в многомерном контексте произвести оптимизацию, перечислив все свои желания и потребности.
Число измерений равно числу величин, необходимых вам для того, чтобы точно определить место в пространстве. Многомерное пространство может быть и абстрактным, например, пространство свойств, которыми должен обладать ваш дом, и конкретным, как реальное физическое пространство, которое мы вскоре рассмотрим. Но покупая дом, вы можете думать о числе измерений как о числе величин, записываемых вами в каждой ячейке базы данных, т. е. числе величин, о которых вам следует поинтересоваться.
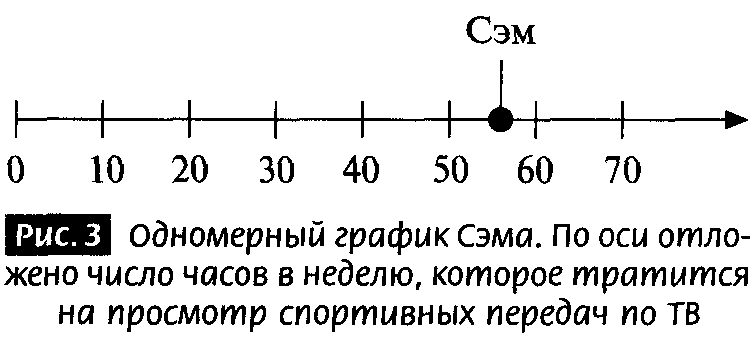
Или рассмотрим неформальный пример применения понятия измерений к людям. Когда вы говорите о ком-то, как об одномерном человеке, вы на самом деле имеете в виду нечто совершенно конкретное: вы считаете, что данный человек интересуется чем-то одним. Например, Сэма, который нигде не работает и сидит дома, смотря спортивные передачи по ТВ, можно описать всего одной порцией информации. Если хотите, вы можете изобразить эту информацию в виде точки на одномерном графике, например, графике склонности Сэма к просмотру спортивных передач. Чтобы начертить такой график, вам нужно определиться с единицами, так чтобы любой другой человек смог бы понять, что означает расстояние вдоль единственной оси. На рис. 3 показан график, на котором точкой на горизонтальной оси отмечен Сэм. График указывает на количество часов в неделю, которые Сэм проводит у экрана ТВ, просматривая спортивные передачи. (К счастью, Сэм не будет оскорблен этим примером; он не входит в число многомерных читателей этой книги.)
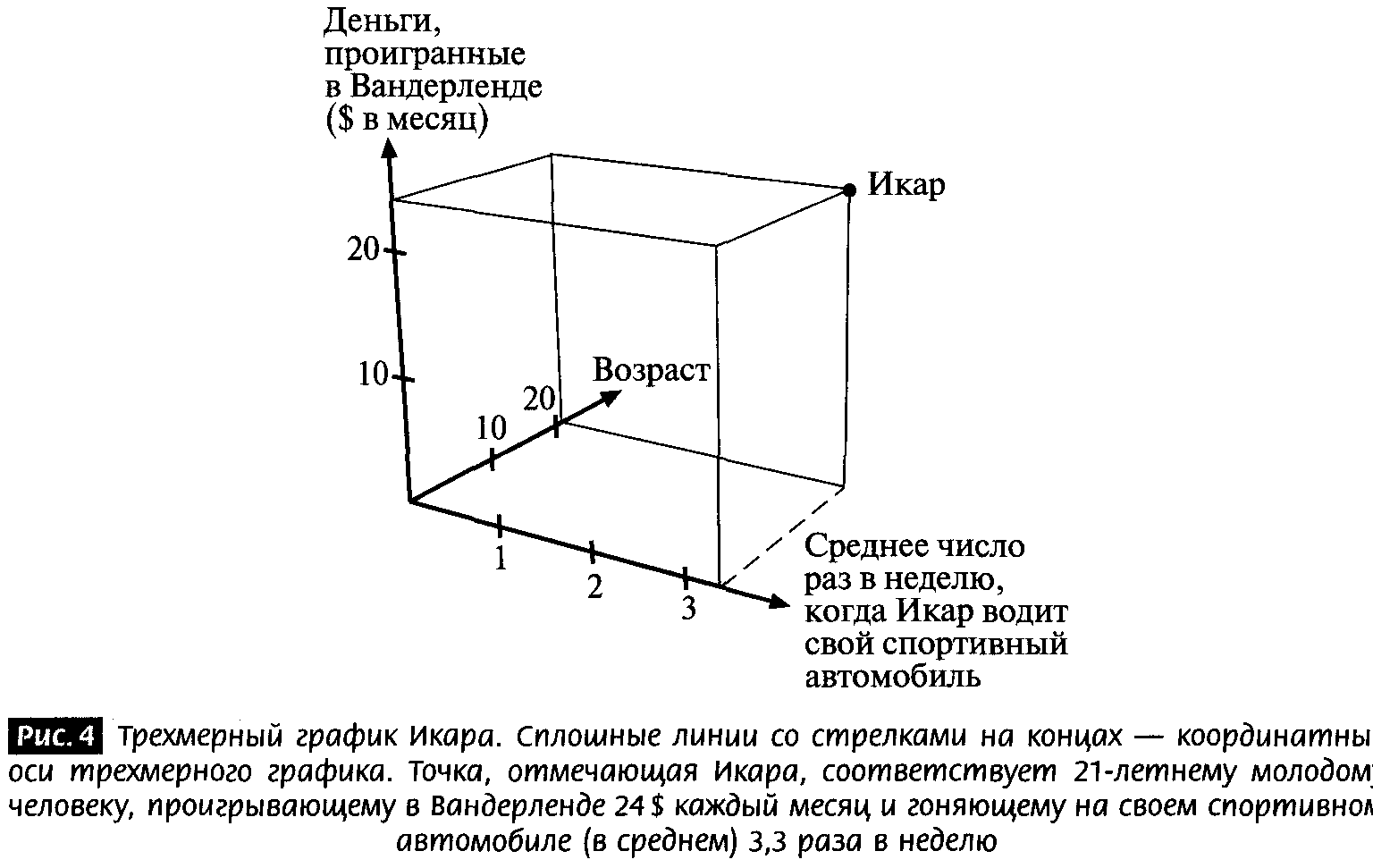
Разовьем это понятие чуть дальше. Икар Рашмор III (из рассказанной выше истории), житель Бостона, — характер посложнее. На самом деле, он трехмерен. Икару двадцать один год, он водит спортивные автомобили и проигрывает деньги в Вандерленде, городе вблизи Бостона, где есть трек для собачьих бегов. На рис. 4 я изобразила Икара. Хотя он и нарисован на двумерной поверхности куска бумаги, наличие трех осей говорит о том, что Икар, безусловно, трехмерен[7].
Однако, описывая большинство людей, мы обычно присваиваем им более одной или даже более трех характеристик. Афине, сестре Икара, одиннадцать лет, она жадно поглощает книги, отличается математическими способностями, интересуется текущими событиями и заботится о маленьких совятах. Вы можете захотеть изобразить все это на графике (хотя зачем это вам, я не очень понимаю). В этом случае Афина будет изображаться точкой в пятимерном пространстве, оси которого соответствуют возрасту, числу прочитанных за неделю книг, среднему числу баллов за тесты по математике, числу минут в день, затрачиваемых на чтение газет, и числу имеющихся в доме совят. Однако нарисовать такой график затруднительно. Для этого потребуется пятимерное пространство, которое очень трудно изобразить. Даже компьютерные программы поддерживают только 3D-графику.
Тем не менее, в абстрактном смысле, существует пятимерное пространство и набор пяти чисел, например (11, 3, 100, 45, 4), говорящих нам, что Афине 11 лет, она в среднем читает 3 книги каждую неделю, всегда отвечает правильно на математические вопросы, тратит каждый день 45 минут на чтение газет и в данный момент в доме живет 4 совы. Этими пятью числами я описала Афину. Если бы вы ее знали, вы могли бы опознать ее по точке в пяти измерениях.
Число измерений для каждого из трех описанных выше людей — это число признаков, использованных мной для их идентификации: один для Сэма, три для Икара и пять для Афины. Конечно, реальных людей в общем случае трудно описать таким небольшим числом единиц информации.
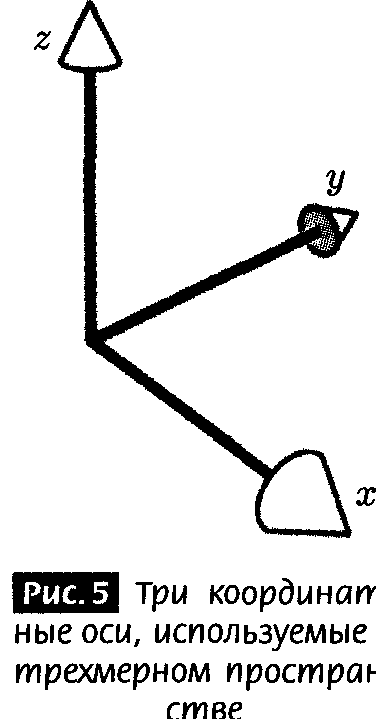
В последующих главах мы будем использовать измерения для описания не людей, а самого пространства. Под «пространством» я понимаю область, в которой существует материя и происходят физические явления. Пространство определенного числа измерений — это-пространство, требующее для задания любой его точки определенного числа величин. В одном измерении это будет точка на графике с единственной осью x; в двух измерениях — точка на графике с осями х и у, в трех измерениях — точка на графике с осями х, у и z[8]. Эти оси показаны на рис. 5.
Все, что нужно для знания вашего точного положения в трехмерном пространстве — это три числа. Задаваемые числа могут быть долготой, широтой и высотой, или длиной, шириной и высотой. Вы можете иным способом выбрать ваши три числа. Решающим является то, что наличие трех измерений означает, что вам требуется ровно три числа. В двумерном пространстве вам требуется два числа, а в пространствах с большим числом измерений вам нужно больше чисел.
Когда число измерений больше, это означает, что вы свободно можете двигаться по большему числу совершенно различных направлений. Точка в четырехмерном пространстве просто требует одну дополнительную ось, которую трудно нарисовать. Но совершенно нетрудно вообразить ее существование. Мы размышляем об этом, используя слова и математические термины.
В теории струн требуется еще больше измерений: эта теория постулирует существование шести или семи дополнительных координат, для того чтобы изобразить точку. Совсем недавние работы по теории струн показали, что число измерений может быть даже еще больше. В этой книге я буду придерживаться открытой точки зрения и допущу возможность существования любого числа дополнительных измерений. Рано говорить, сколько измерений имеет Вселенная на самом деле. Многие представления о дополнительных измерениях, которые я буду описывать, применимы к любому числу дополнительных измерений. В тех редких случаях, когда это будет не так, я об этом скажу специально.
Однако описание физического пространства включает больше, чем простую идентификацию точек. Вам нужно также задать метрику, которая устанавливает масштаб измерений или физическое расстояние между двумя точками. Это соответствует меткам вдоль оси графика. Недостаточно знать, что расстояние между парой точек равно 17, пока вы не знаете, означает ли 17 на самом деле 17 сантиметров, 17 миль или 17 световых лет. Метрика требуется для того, чтобы объяснить, как измерять расстояние, и установить, какому расстоянию в описываемом нами с помощью графика мире соответствует расстояние между двумя точками на этом графике. Метрика дает измерительную линейку, которая определяет ваш выбор единиц, с тем чтобы установить масштаб, аналогично тому, как это делается на карте, когда полдюйма может соответствовать одной миле, или в метрической системе, которая задает метровый эталон, с которым мы все соглашаемся.
Но метрика определяет не только это. Она также говорит нам, изгибается ли, закручивается ли пространство, как поверхность воздушного шара, когда он при надувании превращается в сферу. Метрика содержит всю информацию о форме пространства. Метрика кривого пространства говорит как о расстояниях, так и об углах. Точно так же как сантиметр может соответствовать разным расстояниям, угол может описывать разные формы. Я подробнее расскажу об этом позднее, когда мы будем анализировать связь между кривым пространством и тяготением. Пока что скажем просто, что поверхность шара — совсем не то же самое, что и поверхность плоского листа бумаги. Треугольники на одной поверхности выглядят иначе, чем на другой, и разницу между этими двумерными пространствами можно увидеть в их метрике.
В процессе развития физики менялось и количество информации, спрятанной в метрике. Когда Эйнштейн развивал теорию относительности, он заметил, что четвертое измерение — время — неотделимо от трех измерений пространства. Время тоже нуждается в масштабе, так что Эйнштейн описал гравитацию с помощью метрики четырехмерного пространства-времени, добавив временное измерение к трем пространственным измерениям.
Дальнейшие исследования показали, что могут существовать дополнительные пространственные измерения. В этом случае истинная метрика пространства-времени будет включать более трех измерений пространства. Число измерений и метрика таких измерений определяет то, как мы описываем такое многомерное пространство. Но прежде чем мы исследуем нашу метрику и метрику многомерных пространств подробнее, подумаем еще немного о смысле термина «многомерное пространство».
Игровые пассажи сквозь дополнительные измерения
В книге Роальда Даля «Чарли и шоколадная фабрика» Вилли Вонка представлял посетителям свой «Вонкаватор». По его словам, «лифт может перемещаться только вверх и вниз, а Вонкаватор ходит и вбок, и наискосок, и назад, и вперед, и по сторонам квадрата, и любыми другими способами, которые вы только можете придумать…»[9] Действительно, у Вилли была машина, которая двигалась в любом направлении, до тех пор пока это направление было в тех трех измерениях, о которых мы знаем. Чудесная идея, которая будит воображение!
Однако на самом деле Вонкаватор не мог двигаться по любой дороге, «которую вы только можете придумать». Вилли Вонка проявил невнимательность, когда пренебрег пассажами в дополнительных измерениях. Эти измерения соответствуют совершенно другим направлениям. Их трудно описать, но, может быть, будет легче понять с помощью аналогии.
В 1884 году, для того чтобы объяснить понятие дополнительных измерений, английский математик Эдвин Эбботт написал книгу «Флатландия»[10]. Действие происходит в вымышленной двумерной вселенной по имени Флатландия, где живут двумерные существа (различных геометрических форм). Эбботт показывает, почему флатландцы, вся жизнь которых проходит в двух измерениях, например, на крышке стола, так же сбиты с толку идеей трех измерений, как люди нашего мира поставлены в тупик идеей четырех измерений.
Нам требуется напрячь воображение, чтобы представить более трех измерений, но в стране Флатландии уже три измерения находятся за пределами понимания. Каждый житель этой страны считает очевидным, что во вселенной есть не более двух различных измерений. Жители Флатландии столь же уверены в этом, как жители Земли уверены в наличии трех измерений.
Рассказчик от автора Э. Квадрат (тезка автора Эдвина А. Эбботта) знакомится с реальностью третьего измерения. На первом этапе своего обучения, когда он все еще привязан к Флатландии, он наблюдает трехмерный шар, проходящий вертикально сквозь его двумерный мир. Так как Э. Квадрат привязан к Флатландии, он видит последовательность дисков, размеры которых сначала увеличиваются, а затем уменьшаются. Эти диски представляют собой срезы шара во время его прохождения через плоскость Э. Квадрата (рис. 6).
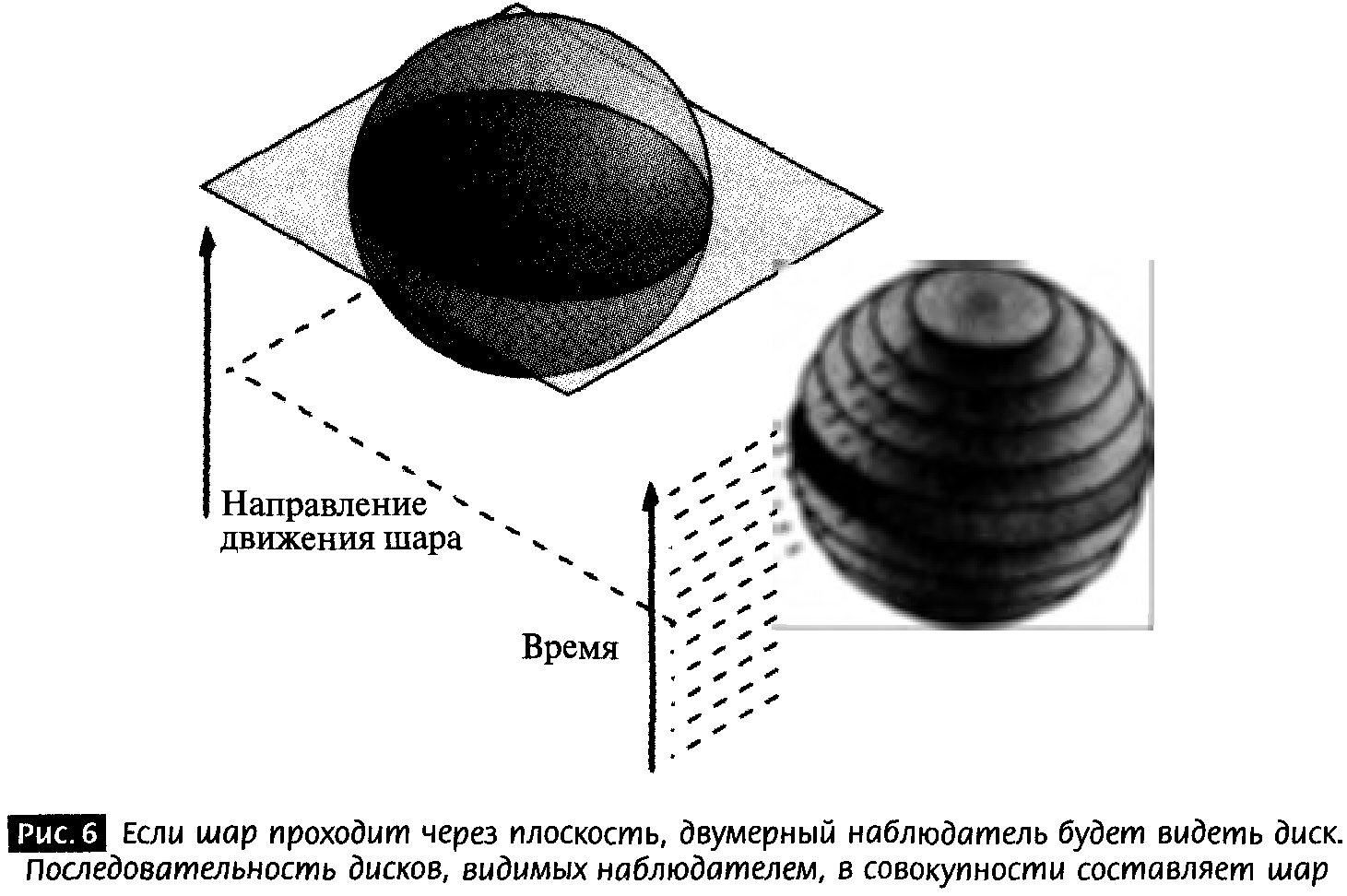
Двумерный наблюдатель, никогда не представлявший себе более двух измерений и никогда не видевший трехмерный объект вроде шара, будет сначала сбит с толку этим зрелищем. Пока Э. Квадрат не сможет подняться из Флатландии в окружающий трехмерный мир, он не сможет по-настоящему вообразить шар. А поднявшись, он постигает шар как образ, созданный склеенными вместе двумерными дисками. Даже в своем двумерном мире, для того чтобы построить шар, Э. Квадрат может начертить видимые им диски как функции времени (см. рис. 6). Но этого не случится до тех пор, пока путешествие сквозь третье измерение не убедит его, что он полностью понимает, что такое шар и его третье пространственное измерение.
По аналогии, мы знаем, что если гиперсфера (шар с четырьмя пространственными измерениями) будет проходить сквозь нашу Вселенную, нам это будет представляться как временная последовательность трехмерных шаров, размеры которых сначала увеличиваются, а затем уменьшаются. К сожалению, у нас нет возможности попутешествовать сквозь дополнительное измерение. Мы никогда не увидим неподвижную гиперсферу во всей полноте. Тем не менее мы можем сделать выводы о том, как эти объекты выглядят в пространствах с разным числом измерений, причем даже тех, которые мы не видим. Мы можем уверенно утверждать, что наше восприятие гиперсферы, движущейся сквозь три измерения, будет похоже на восприятие последовательности трехмерных шаров.
В качестве другого примера вообразим построение гиперкуба — обобщения куба на случай более трех измерений. Линейный отрезок в одном измерении состоит из двух точек, связанных прямой одномерной линией. В случае двух измерений это можно обобщить до квадрата, поместив один из отрезков над другим и соединив их концы двумя дополнительными отрезками. Совершая далее пассаж к кубу в трех измерениях, мы можем построить его, помещая

один двумерный квадрат над другим и связывая их четырьмя дополнительными квадратами, по одному на каждую сторону исходных квадратов (см. рис. 7).
В четырех измерениях куб обобщается до гиперкуба, а в пяти измерениях — до чего-то, чему еще нет названия. Но даже если мы, трехмерные существа, никогда не видели эти два объекта, мы можем обобщить процедуру построения, которая сработала при меньшем числе измерений. Чтобы построить гиперкуб (другое название тессеракт), поместим один куб над другим и свяжем их путем добавления шести дополнительных кубов, соединяющих грани двух исходных. Такое построение представляет абстракцию, которую трудно нарисовать, но это ни в коей мере не делает гиперкуб менее реальным.
Когда я училась в средней школе, я провела лето в математическом лагере (что оказалось намного более интересным, чем вы можете подумать), и там нам показали киноверсию «Флатландии»[11]. В конце диктор с очаровательным британским акцентом безуспешно пытается указать на недоступное флатландцам третье измерение, говоря: «Наверх, а не на север!» К сожалению, мы испытаем ту же неудовлетворенность, если попытаемся указать проход к четвертому пространственному измерению. Но точно так же, как флатландцы не видели или не перемещались сквозь третье измерение, хотя оно и существует в истории Эбботта, тот факт, что мы никогда не видели другого измерения, не означает, что его нет. Итак, хотя мы никогда до сих пор не наблюдали такое измерение и не путешествовали сквозь него, лейтмотивом всей книги «Закрученные пассажи» будет фраза: «Не на север, а вперед вдоль пассажа!» Кто знает, что существует из того, чего мы еще не видели?
Три из двух
В оставшейся части этой главы, вместо того чтобы размышлять о пространствах, имеющих более трех измерений, я поговорю о том, как с помощью наших ограниченных зрительных возможностей мы собираемся представлять и рисовать три измерения, используя двумерные образы. Понимание того, как мы совершаем этот пассаж от двумерных образов к трехмерной реальности, пригодится позднее, когда мы будем интерпретировать малоразмерные «картинки» многомерных миров. Относитесь к этому разделу как к разминочному упражнению, для того чтобы приучить ваш мозг к дополнительным измерениям. Было бы неплохо помнить, что в обычной жизни вы все время имеете дело с размерностью. На самом деле все это не так уж незнакомо.
Часто все, что мы можем видеть, — это кусочки поверхностей, которые обрамляют вещи. Хотя эта внешняя оболочка и изгибается в трехмерном пространстве, она имеет два измерения, так как для определения положения любой точки на ней нужно задать два числа. Мы приходим к выводу, что поверхность не трехмерна, так как у нее нет толщины.
Смотря на картины, экраны кинотеатров, мониторы компьютеров или рисунки в этой книге, мы, вообще говоря, смотрим не на трехмерные, а на двумерные изображения. Но тем не менее мы можем восстановить изображенную трехмерную реальность.
Для построения трех измерений мы можем использовать двумерную информацию. Этот процесс включает урезание информации при создании двумерных представлений и одновременно попытку сохранить достаточно информации для воспроизводства важных элементов исходного объекта. Обратимся к часто используемым методам сведения объектов более высокой размерности к меньшему числу измерений: нарезка слоями, проектирование, голография и иногда просто пренебрежение размерностью, — и обратному процессу восстановления тех трехмерных объектов, которые они представляют.
Наименее сложный способ заглянуть за поверхность — сделать тонкие слои. Каждый слой двумерен, но комбинация слоев образует реальный трехмерный объект. Например, когда вы покупаете ветчину в магазине, трехмерный кусок окорока быстро нарезают на много двумерных ломтей[12]. Складывая все ломти, можно реконструировать форму всего трехмерного куска.
Эта книга трехмерна. Однако ее страницы имеют только два измерения. Объединение двумерных страниц образует книгу[13]. Можно многими разными способами проиллюстрировать это объединение. Один способ показан на рис. 8, на котором мы смотрим на книгу сбоку. На этом рисунке мы опять играем с размерностью, так как каждая линия представляет страницу. Поскольку все мы знаем, что линии соответствуют двумерным страницам, эта иллюстрация всем ясна. Позднее мы используем аналогичный подход, чтобы изобразить объекты в многомерных мирах.


Разрезание на слои — лишь один из способов заменить высшие измерения более низкими. Другим способом является проектирование — технический термин, заимствованный из геометрии. Проектирование содержит строгие предписания для создания образа объекта, имеющего меньшее число измерений. Тень на стене — один из примеров двумерной проекции трехмерного объекта. На рис. 9 показано, каким образом теряется информация, когда мы (или кролики) осуществляем проектирование. Точки на тени определяются только двумя координатами, лево — право или вверх — вниз на стене. Однако проектируемый объект имеет третье пространственное измерение, которое не сохраняется в проекции.
Простейший способ осуществить проектирование состоит в том, чтобы отбросить одно измерение. Например, на рис. 10 показан куб в трех измерениях, спроектированный на два измерения. Проекция куба может иметь много форм, простейшая из которых есть квадрат.

Возвращаясь к предыдущим примерам графиков Икара и Афины, мы можем построить двумерный график Икара, если пренебрежем его вождением спортивных автомобилей. На самом деле нам не важно, сколько сов выращивает Афина, поэтому мы можем построить не пятимерный, а четырехмерный график. Пренебрежение совами Афины и есть проектирование.
Проекция теряет информацию об исходном многомерном объекте (рис. 9). Однако, когда с помощью проектирования мы создаем картину с меньшим числом измерений, мы иногда добавляем информацию, помогающую восстановить часть потерянного. Дополнительной информацией может быть штриховка или цвет, как в живописи или фотографии. Это может быть число, как на топографических картах для указания высоты местности. Наконец, какие-либо метки могут вообще отсутствовать, и в этом случае двумерное описание просто несет меньше информации.
Если бы не оба наших глаза, работающих совместно и позволяющих реконструировать три измерения, все, что мы видим, было бы проекциями. Если закрыть один глаз, восприятие глубины становится грубее. Один глаз создает двумерную проекцию трехмерной реальности. Чтобы воспроизвести три измерения, нужны два глаза.
У меня близорукость на одном глазу и дальнозоркость на другом, поэтому я не могу должным образом объединять изображения от обоих глаз, если не надеваю очков (что случается редко). Хотя мне сказали, что у меня будут проблемы с реконструкцией трех измерений, обычно я этих проблем не замечаю — все вокруг меня выглядит трехмерным. Это происходит потому, что для реконструкции трехмерных образов я полагаюсь на тени и перспективу (и свое знакомство с внешним миром).
Однако однажды в пустынной местности мы с другом пытались дойти до далекого утеса. Мой друг убеждал меня, что мы должны двигаться прямо, а я никак не могла понять, почему он настаивает, чтобы мы шли прямо сквозь скалу. Оказалось, что скала, про которую я думала, что она выступает непосредственно из утеса, полностью загораживая нам путь, находилась на самом деле значительно ближе к нам, перед утесом. Эта скала, которая, как мне казалось, преградит нам путь, на самом деле вообще не имела отношения к утесу. Путаница возникла из-за того, что мы были вблизи утеса около полудня, когда нет никаких теней, и у меня не было способа построить третье измерение, которое бы указало мне, каким образом далекие утесы и скалы расположены относительно друг друга. Я никогда не осознавала своей компенсирующей стратегии с использованием теней и перспективы, до тех пор пока она не дала сбой.
Живопись и черчение всегда требуют, чтобы художники сводили все, что они видят, к спроектированным образам. В средневековом искусстве это делалось максимально простым образом. На рис. 11 показано мозаичное изображение города в виде двумерной проекции. Ничто на этой мозаике не указывает на третье измерение, нет никаких меток или индикаторов его существования.
Со времен Средневековья художники разработали способы делать такие проекции, которые частично исправляют потерю на картине одного измерения. Один подход, противоположный средневековому уплощению пространства, это метод, использованный кубистами в двадцатом веке. Кубистическая картина (например, «Портрет Доры Маар» Пикассо, рис. 12 представляет одновременно несколько проекций, каждая из которых получена под другим углом, и поэтому передает ощущение трехмерности субъекта.


Однако большинство западноевропейских художников со времен Ренессанса для создания иллюзии третьего измерения использовали перспективу и затенение. Одним из важнейших навыков в живописи является способность так свести трехмерный мир к двумерному представлению, чтобы зритель мог обратить процесс и восстановить исходную трехмерную сцену или объект. Наше культурное воспитание приучило нас знать, как расшифровывать образы, даже при отсутствии полной трехмерной информации.
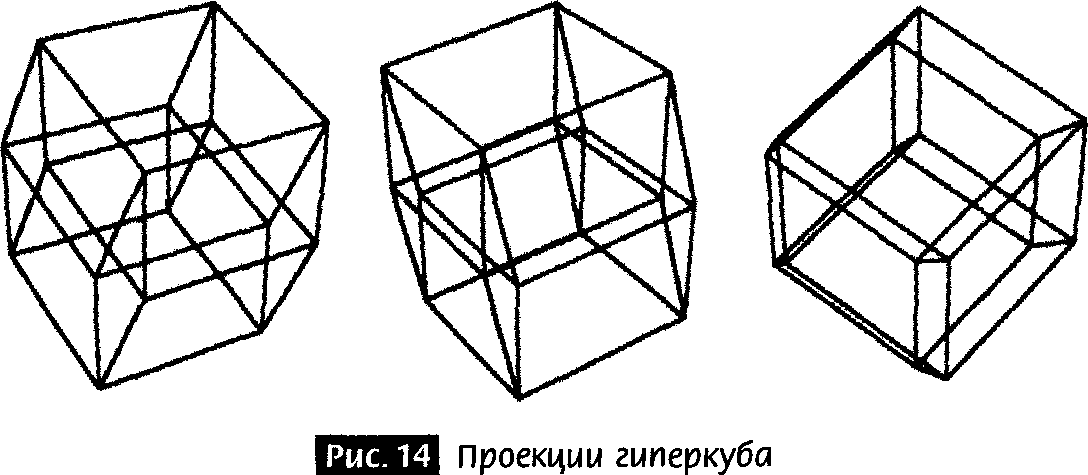
Художники пытались даже представить на двумерных плоскостях многомерные объекты. Например, на картине Сальвадора Дали «Распятие» (Corpus Нуpercubus) (рис. 13) крест показан как развернутый гиперкуб. Этот объект состоит из восьми кубов, прикрепленных друг к другу в четырехмерном пространстве. Именно эти кубы Дали и нарисовал. На рис. 14 я показываю несколько проекций гиперкуба.
Я уже упоминала физический пример — квазикристаллы, которые выглядят как проекции многомерного кристалла на наш трехмерный мир. Проекции можно также использовать для практических, а не только художественных целей. В медицине есть много примеров, когда трехмерные объекты проектируются на два измерения. Рентген органов всегда фиксирует двумерную проекцию. В методе компьютерной томографии изображения складываются из множества рентгеновских снимков и реконструируют более информативное трехмерное представление. Имея в распоряжении рентгеновские снимки, сделанные под достаточно большим числом углов, можно использовать интерполяцию, чтобы собрать полные трехмерные изображения. С другой стороны, магнито-резонансное сканирование восстанавливает трехмерный объект по срезам.
Другим способом записи трех измерений на двумерной поверхности является голографическое изображение. Хотя голографическое изображение записывается на поверхности меньшей размерности, оно на самом деле несет всю информацию об исходном пространстве большей размерности. Возможно, один из образцов такой техники лежит в вашем кошельке: трехмерное изображение на вашей кредитной карте и есть голограмма.
Голографическое изображение записывает взаимосвязи между светом в разных местах, так что затем можно восстановить всю многомерную картину. Этот принцип во многом похож на тот, который используется в хорошем стереопроигрывателе, позволяющем слышать, где находились одни инструменты по отношению к другим во время записи. С помощью информации, запасенной в голограмме, глаз действительно может реконструировать тот трехмерный объект, который эта голограмма представляет.
Перечисленные методы показывают, как можно получить больше информации от образа с меньшим числом измерений. Однако, может быть, все, что нам действительно нужно, так это поменьше информации. Часто мы просто не обращаем внимания на все три измерения. Например, нечто может быть настолько тонким в третьем измерении, что в этом направлении не происходит ничего интересного. Даже несмотря на то, что краска на этой странице реально трехмерна, мы ничего не потеряем, если будем считать ее двумерной. До тех пор, пока мы не посмотрим на страницу под микроскопом, у нас просто нет достаточного разрешения, чтобы увидеть толщину краски. Проволока выглядит одномерной, хотя при более близком рассмотрении вы можете увидеть, что она имеет двумерное поперечное сечение, и тем самым все три измерения.
Эффективные теории
Нет ничего ошибочного в пренебрежении дополнительным измерением, если оно слишком мало, чтобы его видеть. Обычно можно пренебречь не только зрительными эффектами, но также и физическими явлениями, связанными с очень слабыми, недетектируемыми процессами. При формулировке своих теорий или проведении вычислений ученые часто пренебрегают (иногда непреднамеренно) физическими процессами, происходящими на не поддающихся измерению малых масштабах, или производят по ним усреднение. Законы движения Ньютона работают на расстояниях и при скоростях, которые он мог наблюдать. Для того чтобы делать успешные предсказания, ему не нужны были детали общей теории относительности. Когда биологи изучают клетку, им не нужно знать про кварки внутри протона.
Отбор существенной информации и пренебрежение деталями — это тип прагматичного обмана, которым каждый занимается ежедневно. Это способ борьбы с избытком информации. Почти для всего, что вы видите, слышите, осязаете, обоняете или пробуете на вкус, у вас есть выбор между доскональным изучением деталей или осмыслением «картины в целом» с другой системой ценностей. Разглядываете ли вы картину, пробуете вино, читаете книгу по философии или планируете предстоящее путешествие, вы автоматически разделяете свои мысли на категории, представляющие интерес, будь то размеры, запахи или идеи, и категории, которые в данный момент кажутся вам несущественными. При соответствующем отборе вы игнорируете некоторые детали, так что можете сфокусировать внимание на интересующем вас вопросе и не затемнять его несущественными деталями.
Такая процедура отбрасывания мелкой информации должна быть знакома каждому, так как на самом деле такое концептуальное действие люди совершают все время. Возьмем, например, жителей Нью-Йорка. Те из них, которые живут в центре города, видят детали и различия внутри Манхэттена. Для них центр города грязнее, старее, с узкими, искривленными улицами. А вот в спальных районах больше домов, предназначенных для нормальной жизни, там находится Центральный парк и большинство музеев. Хотя при взгляде издалека такие различия размываются, внутри города они очень существенны.
Но подумайте теперь о том, как видят Нью-Йорк люди, живущие далеко. Для них этот город — точка на карте. Возможно, важная точка, обладающая определенным характером, но, тем не менее, всего лишь точка, если глядеть извне. При всем своем разнообразии, жители Нью-Йорка образуют одну категорию, если смотреть, например, со Среднего Востока или из Казахстана. Когда я упомянула об этой аналогии моему кузену, который живет в центре (чтобы быть точной, в Вест Виллидж), он подтвердил мою точку зрения, и сказал, что нельзя объединять в одну группу всех обитателей Нью-Йорка, живущих и в центре, и на окраинах города. Тем не менее, как может возразить ему любой человек не из Нью-Йорка, различия слишком малы, чтобы иметь значение для людей, не живущих в нашей среде.
Для физики характерна формализация этого интуитивного ощущения, с формированием категорий по подходящим значениям расстояния или энергии. Физики используют такой подход и даже дали ему имя — эффективная теория. Такая теория сосредоточивает внимание на частицах и силах, которые приводят к «эффектам» на рассматриваемом расстоянии. Вместо того чтобы описывать частицы и взаимодействия, используя неизмеримые параметры, отвечающие поведению при сверхвысоких энергиях, мы описываем наблюдения с помощью понятий, которые действительно важны на тех масштабах, которые можно обнаружить. Эффективная теория на любом заданном масштабе расстояний не интересуется деталями лежащей в основе физической теории на малых расстояниях, а задает вопросы только о вещах, которые можно надеяться увидеть или измерить. Если что-то находится за пределами разрешения тех масштабов, на которых вы работаете, вам и не нужно знать его детальную структуру. Подобная практика — это не научное мошенничество, а способ избавиться от неразберихи, связанной с избыточной информацией. Это «эффективный» способ разумно получить правильные ответы.
Всякий, включая физиков, счастлив вернуться в трехмерную вселенную, если многомерные детали находятся вне области, где мы их можем различать. Аналогично тому, как физики часто рассматривают проволоку так, как будто она одномерна, мы также будем описывать вселенную с большим числом измерений с помощью понятий теорий малой размерности, когда дополнительные измерения крошечны и детали дополнительных измерений слишком малы, чтобы иметь значение. Такое маломерное описание будет суммировать наблюдаемые эффекты всех возможных теорий с большим числом измерений, в которых дополнительные измерения слишком малы, чтобы их видеть. Для многих целей такое маломерное описание является адекватным, независимо от числа, размера и формы дополнительных измерений.
Маломерные величины не обеспечивают фундаментального описания, но они представляют удобный способ организации наблюдений и предсказаний. Если вы знаете детали поведения на малых расстояниях или микроструктуру теории, вы можете использовать их для вывода величин, возникающих в описании при низких энергиях. В противном случае такие величины являются просто неизвестными, подлежащими экспериментальному обнаружению.
В следующей главе мы развиваем эти идеи и рассматриваем следствия существования крохотных свернутых дополнительных измерений. Те измерения, которые мы рассмотрим сначала, являются очень маленькими, слишком крохотными для того, чтобы приводить к каким-то различиям. Далее, когда мы вернемся к дополнительным измерениям, мы исследуем также большие и бесконечные измерения, которые недавно радикально изменили эту картину.
Глава 2
Ограниченные пассажи: свернутые дополнительные измерения
No way out
None whatsoever.
Jefferson Starship[14]
Афина проснулась сразу. Накануне она читала «Алису в стране чудес» и «Флатландию», чтобы проникнуться вдохновляющими идеями в отношении измерений. А ночью ей приснился необычайно странный сон, который явился, как она поняла, уже полностью очнувшись от сна, результатом одновременного чтения сразу двух книг[15].
Афине снилось, что она превратилась в Алису, проскользнула в кроличью нору и встретила хозяина. Кролика, который вытолкнул ее в незнакомый мир. Афина подумала, что это довольно грубый способ обращения с гостем. Несмотря на это, она страстно предвкушала предстоящее приключение в Волшебной стране.
Однако Афина была разочарована. Хозяин Кролик, обожавший каламбуры, послал ее вместо этого в 1D-ленд[16], странный, но не такой уж волшебный одномерный мир. Афина огляделась, или, правильнее сказать, посмотрела налево и направо, и обнаружила, что все, что она может видеть, это две точки — одна слева от нее, другая справа (и, как ей показалось, более симпатичного цвета).
В 1D-ленде все одномерные жители со своими одномерными владениями были выстроены вдоль этого единственного измерения какдлинные, тонкие бусинки, нанизанные на нить. Но даже при ограниченности своего кругозора Афина знала, что в 1D-ленде есть что-то еще, кроме того, что видят ее глаза, так как в ее уши проникал страшный шум. черная Королева была хорошо спрятана за точкой, но Афина не могла перепутать ее скрипучие пронзительные крики: «Никогда не видела более нелепой шахматной партии! Я не могу двигать ни одной фигурой, даже ладьей!» Афина успокоилась, когда поняла, что одномерное существование защищает ее от гнева Черной королевы.
Но уютная вселенная Афины просуществовала недолго. Проскользнув сквозь щель в 1D-ленде, она вернулась в кроличью нору, в которой был лифт, способный перенести ее во вселенные с другим числом измерений. Почти сразу же Кролик объявил: «Следующая остановка — Двумерная страна». Афина отметила про себя, что 2D-ленд[17] — не очень приятное название, но все равно осторожно вышла из лифта.
Афине незачем было так долго колебаться. Почти все в 2D-ленде выглядело так же, как в 1D-ленде. Она заметила лишь одно отличие — бутылочку с этикеткой «Выпей меня». Афине было скучно в одном измерении, так что она немедленно подчинилась. Она быстро сократилась до крохотного размера, и пока она уменьшалась, все явственнее проступало второе измерение. Это второе измерение было совсем небольшим и было свернуто в маленькую окружность. Местность вокруг Афины напоминала теперь поверхность очень длинной трубки, по окружности носился Додо, но ему хотелось остановиться. Поэтому он любезно предложил довольно проголодавшейся Афине кусок кекса.
Пока Афина ела волшебный кекс Додо, она начала расти, проглотив всего несколько кусочков (она была уверена в этом, так как осталась голодной), она обнаружила, что кекс практически исчез и от него осталась лишь очень маленькая крошка. По крайней мере, Афине казалось, что это была крошка, хотя ее можно было разглядеть, только сильно сощурившись. Не только кекс исчез из вида: когда Афина вернулась к своему обычному размеру, все второе измерение полностью исчезло.
«2D-ленд — очень странное место. Лучше я вернусь домой», — подумала Афина. Ее обратное путешествие тоже не обошлось без приключений, но рассказ о них мы отложим до следующего раза.
Хотя мы и не знаем, почему три пространственных измерения являются особенными, можно спросить: как это возможно? Как так может быть, что нам кажется, что во Вселенной только три пространственных измерения, если в изначальном фундаментальном пространстве-времени их больше? Если Афина находится в двумерном мире, почему она иногда видит только одно измерение? Если теория струн правильно описывает природу, и существуют девять пространственных (плюс одно временное) измерений, то что случилось с шестью исчезнувшими пространственными измерениями? Почему они не видны? Оказывают ли они какое-то заметное влияние на видимый нами мир?
Последние три вопроса являются центральными для этой книги. Однако прежде всего следует определить, существует ли какой-то способ скрыть свидетельства существования дополнительных измерений, так чтобы двумерный мир Афины казался одномерным, а вселенная с дополнительными измерениями казалась бы трехмерной пространственной структурой, которую мы и наблюдаем. Если мы примем идею мира с дополнительными измерениями, из какой бы теории они ни возникали, должно существовать хорошее объяснение того, почему мы до сих пор не зафиксировали ни малейших следов их существования.
Эта глава посвящена чрезвычайно малым, так называемым компактифицированным, или свернутым, измерениям. Они не простираются до бесконечности, как три привычные нам измерения, напротив, они быстро сворачиваются в петли, как туго намотанная катушка ниток. Никакие два тела не могут быть удалены друг от друга на большое расстояние вдоль компактифицированного измерения; всякая попытка совершить экскурсию на большое расстояние обернется вместо этого путешествием по кольцу, вроде беготни Додо. Подобные компактифицированные измерения могут быть такими маленькими, что мы никогда не заметим их существования. Как мы поймем в дальнейшем, если крохотные свернутые измерения существуют, то их обнаружение является непростой задачей.
Свернутые измерения в физике
Теория струн — наиболее многообещающий кандидат на теорию, объединяющую квантовую механику и тяготение, — дает конкретный повод для размышлений о дополнительных измерениях. Действительно, единственные известные нам согласованные версии теории струн обременены этими удивительными придатками. Однако, хотя появление теории струн в мире физики укрепило респектабельность дополнительных измерений, сама идея этих измерений возникла значительно раньше.
В начале двадцатого века теория относительности Эйнштейна распахнула двери для идеи о возможном существовании дополнительных измерений пространства. Теория относительности описывает тяготение, но эта теория не говорит нам, почему мы ощущаем то конкретное тяготение, которое мы знаем. Теория Эйнштейна не отдает предпочтения никакому конкретному числу пространственных измерений. Она одинаково хорошо работает в случае трех, четырех или десяти измерений. Почему же тогда кажется, что их только три?
В 1919 году, следуя по пятам за эйнштейновской общей теорией относительности (завершенной в 1915 году), польский математик Теодор Калуца заметил эту черту теории Эйнштейна и смело предположил существование четвертого пространственного измерения, нового невидимого измерения у пространства[18]. Он полагал, что дополнительное измерение должно как-то отличаться от трех знакомых бесконечных измерений, хотя не уточнил как. Целью Калуцы при введении лишнего измерения было объединение сил тяготения и электромагнетизма. Хотя детали этой неудавшейся попытки объединения сейчас несущественны, дополнительное измерение, которое он столь дерзко ввел, оказалось очень к месту.
Калуца написал свою статью в 1919 году. Эйнштейн, который был рецензентом журнала и оценивал возможность публикации статей в научном журнале, колебался в отношении достоинств этой идеи. Он задержал публикацию статьи Калуцы на два года, но в конце концов признал ее оригинальность. Но Эйнштейн все же хотел знать, чем было это измерение. Где оно было и чем отличалось от других? Насколько далеко оно простиралось?
Эти вопросы были очевидными. Те же самые вопросы могут тревожить и вас. На вопросы Эйнштейна не было никакого отклика вплоть до 1926 года, когда шведский математик Оскар Клейн задумался над ними. Клейн предположил, что дополнительное измерение может быть свернуто в форме окружности и быть чрезвычайно малым, равным 10-33 см[19], т. е. одной миллиардной от триллион триллионной доли сантиметра. Такое крохотное свернутое измерение должно существовать везде, иначе говоря, в каждой точке пространства должна существовать своя крохотная окружность размером 10-33 см.
Эта маленькая величина представляет собой планковскую длину, величину, которая будет для нас существенной позднее, когда мы детальнее обсудим гравитацию. Клейн выбрал планковскую длину потому, что это единственная длина, которая может естественно возникнуть в квантовой теории гравитации, а гравитация связана с формой пространства. Пока что все, что нам нужно знать о планковской длине, — это то, что она чрезвычайно, невообразимо мала, много меньше, чем все, что мы когда-либо будем иметь шанс измерить. Она на двадцать четыре порядка величины[20] меньше размера атома и на девятнадцать порядков величины меньше протона. Нетрудно проглядеть что-то столь же маленькое, как это.
В повседневной жизни есть много примеров вещей, протяженность которых в одном из трех обычных измерений слишком мала, чтобы быть замеченной. Картина на стене или бельевая веревка с большого расстояния кажутся протяженными не в трех, а в меньшем числе измерений. Мы не видим толщину слоев краски или толщину веревки. Для обычного наблюдателя картина выглядит так, как будто у нее только два измерения, а веревка для белья кажется имеющей только одно, даже если мы знаем, что на самом деле эти вещи имеют три измерения. Единственный способ разглядеть трехмерную структуру таких вещей — посмотреть на них поближе или с достаточно хорошим разрешением. Если мы протянем шланг через футбольное поле и посмотрим на него с вертолета, как показано на рис. 15, шланг будет казаться одномерным. Но с близкого расстояния вы можете различить два измерения поверхности шланга и трехмерный объем, который эта поверхность ограничивает.
Однако для Клейна неразличимо мала была не толщина какой-то вещи, а малым было само измерение. Так что же означают слова, что измерение мало? Как будет выглядеть вселенная со свернутым измерением с точки зрения того, кто живет в ней? Опять же ответ на этот вопрос зависит полностью от размера свернутого измерения. Рассмотрим пример, показывающий, как будет выглядеть мир для разумных существ, которые слишком малы или, наоборот, слишком велики по сравнению с размером свернутого дополнительного измерения. Поскольку нарисовать четыре или больше измерений невозможно, то на первом рисунке я представлю вселенную с малым компактифицированным измерением, имеющую только два измерения, причем одно из них туго скручено до очень малого размера (рис. 16).
Представьте снова садовый шланг, который можно рассматривать как длинный резиновый лист, свернутый в трубку малого поперечного сечения. На этот раз мы полагаем, что шланг — это вся вселенная (а не объект внутри вселенной)[21]. Если бы вселенная имела форму такого садового шланга, у нас было бы одно очень длинное измерение и одно очень маленькое, свернутое измерение. Это именно то, что мы хотим.

Для небольшого существа, например, плоского жука, живущего во вселенной садового шланга, она выглядела бы двумерной. (В таком сценарии наш жук должен быть приклеен к поверхности шланга — двумерная вселенная не включает внутренность шланга, которая трехмерна.) Жук может ползать в двух направлениях: вдоль шланга или вокруг него. Как Додо, который мог бегать по кругу в своей двумерной вселенной, жук, начавший движение из какой-то точки на шланге, может проползти вокруг него и в конце концов вернуться к тому месту, с которого начал. Так как второе измерение мало, жуку не придется слишком далеко уползать, чтобы вернуться.
Если популяция живущих на шланге жуков испытывает воздействие сил, например, электрических или гравитационных, эти силы способны притягивать или отталкивать жуков в любом направлении по поверхности шланга. Жуки могут быть отделены друг от друга либо вдоль длины шланга, либо по его окружности, и могут испытывать действие любой силы, присутствующей на шланге. Если разрешение достаточно для того, чтобы различать столь малые расстояния, как диаметр шланга, силы и тела проявляют оба измерения, которые и есть на самом деле.
Однако, если бы наш жук мог обозреть окружающее его пространство, он бы заметил, что два измерения очень различны. Одно измерение, вдоль длины шланга, очень большое. Он может быть даже бесконечно большим. В то же время другое измерение очень мало. Два жука никогда не расползутся очень далеко друг от друга в направлении вокруг шланга. И жук, пытающийся совершить далекое путешествие в этом направлении, очень скоро попадет туда, откуда он начал свой путь. Сообразительный жук, любящий тренировать свои ноги, знал бы, что его вселенная двумерна, и что одно измерение тянется далеко-далеко, а другое очень мало и свернуто в окружность.
Однако точка зрения жука совершенно отлична от точки зрения, которую имели бы существа вроде нас во вселенной Клейна, в которой дополнительное измерение свернуто до чрезвычайно малого размера, равного 10-33 см. В отличие от жука мы никогда не станем достаточно маленькими, чтобы обнаружить или прогуляться по измерению столь малого размера.
Итак, чтобы завершить нашу аналогию, предположим, что во вселенной садового шланга живет существо, значительно большее, чем жук, обладающее только грубым разрешением и поэтому не способное детектировать малые тела или структуры. Так как линза, через которую большое существо наблюдает за миром, смазывает все детали, столь же малые как диаметр шланга, то с точки зрения этого существа дополнительное измерение будет невидимым. Существо будет видеть только одно измерение. Понять, что вселенная садового шланга имеет более одного измерения, можно, только если обладать зрением столь острым, чтобы различить нечто столь малое, как ширина шланга. Но если зрение не такое острое, чтобы различить эту ширину, существо всегда будет видеть только линию.
Кроме того, физические явления не выдадут существования дополнительного измерения. Большие существа во вселенной садового шланга заткнут второе, маленькое измерение и никогда не узнают, что оно здесь было. Не имея возможности обнаружить структуру или изменения вдоль дополнительного измерения типа раскачки или волн материи или энергии, они никогда не зарегистрируют его существование. Любые изменения вдоль второго измерения будут полностью смыты, подобно тому как вы никогда не заметите какое-либо изменение толщины листа бумаги в масштабе его атомной структуры.
Двумерный мир, в котором оказалась во сне Афина, был очень похож на вселенную садового шланга. Так как у Афины были возможности становиться как большой, так и малой относительно ширины 2D-ленда, она могла наблюдать эту вселенную как с точки зрения кого-то большего по размерам, по сравнению со вторым измерением этой вселенной, так и с точки зрения кого-то меньшего по размерам. Для большой Афины 2D-ленд и 1D-ленд выглядели полностью одинаковыми. Только маленькая Афина могла указать на различие. Так и во вселенной садового шланга существо будет находиться в полном неведении относительно дополнительного пространственного измерения, если не станет достаточно маленьким, чтобы его увидеть.
Вернемся к вселенной Калуцы — Клейна, у которой есть три известных нам пространственных измерения и дополнительное невидимое измерение. Чтобы обдумать ситуацию, можно опять использовать рис. 16. В идеале, мне следовало бы нарисовать четыре пространственных измерения, но, к сожалению, это невозможно (не поможет даже книжка-раскладушка с объемными разворотами). Однако, поскольку три бесконечных измерения, образующих наше пространство, качественно одинаковы, мне нужно реально нарисовать только одно типичное измерение. Это позволяет мне использовать другое измерение, чтобы представить невидимое дополнительное измерение. Показанное здесь другое измерение свернуто и этим оно фундаментально отличается от трех других.
Точно так же как в примере с двумерной вселенной садового шланга, четырехмерная вселенная Калуцы — Клейна с одним крохотным свернутым измерением будет казаться нам имеющей на одно измерение меньше, чем те четыре, которые есть на самом деле. Так как мы ничего не можем знать о дополнительном пространственном измерении, пока не сумеем получить свидетельство о его структуре в крохотном масштабе этого измерения, вселенная Калуцы — Клейна будет казаться трехмерной. Свернутые или компактифицированные дополнительные измерения никогда не будут обнаружены, если их масштабы достаточно малы. Позднее мы исследуем вопрос, насколько они должны быть малы, однако сейчас достаточно понимать, что планковская длина находится далеко за порогом измеримости.
В жизни и в физике мы регистрируем только те детали, которые действительно для нас важны. Если вы не можете наблюдать детальную структуру, вы можете с тем же успехом считать, что ее нет. В физике это пренебрежение локальными деталями реализуется в идее эффективной теории, о чем шла речь в предыдущей главе. Все, что имеет значение в эффективной теории, — это вещи, которые вы можете реально воспринимать. В приведенном выше примере мы будем использовать трехмерную эффективную теорию, в которой подавлена информация о дополнительных измерениях.
Хотя свернутое измерение во вселенной Калуцы — Клейна находится рядом с нами, оно так мало, что любое изменение в нем является незаметным. Точно так же, как различия между жителями Нью-Йорка не имеют никакого значения для приезжего, структура дополнительных измерений вселенной несущественна, когда ее детали изменяются в столь крохотном масштабе. Даже если окажется, что на фундаментальном уровне имеется много больше измерений, чем те, с которыми мы знакомы в повседневной жизни, все, что мы видим, будет описываться с помощью тех измерений, которые мы наблюдаем. Экстремально малые дополнительные измерения ничего не изменяют в нашем видении мира, или даже в том, как мы производим большинство физических расчетов. Даже если дополнительные измерения существуют, но мы неспособны видеть их или знать о них по опыту, то можно ими пренебречь и при этом правильно описывать то, что мы видим. Позднее я познакомлю вас с модификациями этой простой картины, для которых это не всегда будет справедливо, но они будут включать дополнительные предположения.
Еще один важный момент, касающийся свернутого измерения, можно понять из рис. 17, где показан шланг или вселенная с одним измерением, свернутым в окружность. Возьмем любую точку вдоль бесконечного измерения. Заметим, что в каждой без исключения точке находится полное компактное пространство, а именно, окружность. Шланг состоит из всех таких окружностей, склеенных вместе, как те слои, о которых шла речь в гл. 1.

На рис. 18 приведен другой пример. Здесь имеются не одно, а два бесконечных измерения, и одно дополнительное измерение, свернутое в окружность. В этом случае окружность находится в каждой без исключения точке двумерного пространства. И если бы было три пространственных измерения, свернутые измерения существовали бы в каждой точке трехмерного пространства. Вы можете сравнить точки в пространстве с дополнительными измерениями с клетками вашего тела, каждая из которых содержит принадлежащую вам полную последовательность ДНК. Аналогично, каждая точка в вашем трехмерном пространстве должна быть хозяйкой полностью компактифицированной окружности.
До сих пор мы рассматривали только одно дополнительное измерение, свернутое в окружность. Но все, что было сказано, должно выполняться и тогда, когда свернутое измерение принимает другую, вообще говоря, любую форму. Может случиться и так, что имеется два или более крохотных свернутых измерений любой формы. Все без исключения измерения, которые достаточно малы, будут для нас совершенно невидимыми.
Рассмотрим пример с двумя свернутыми измерениями. Эти свернутые измерения могут принимать много разных форм. Мы выберем тор, имеющий форму бублика, в котором два дополнительных измерения одновременно свернуты в окружности. Это показано на рис. 19. Если обе окружности — та, которая навивается через дырку в бублике, и та, которая навивается вокруг самого бублика, — достаточно малы, мы никогда не увидим двух дополнительных свернутых измерений.
Но это только один пример. В случае большего числа измерений имеется огромное количество возможных компактных пространств, т. е. пространств со свернутыми измерениями, отличающихся друг от друга конкретным способом, которым эти измерения свернуты. Одной категорией компактных пространств, важных для теории струн, являются многообразия Калаби — Яу, названные по именам итальянского математика Эудженио Калаби, первым предложившего эти особые формы, и уроженца Китая гарвардского математика Шин Тун Яу, показавшего, что эти формы математически возможны. В этих геометрических формах дополнительные измерения свернуты и закручены весьма необычным способом. Как и во всех случаях компактификации, измерения сворачиваются на малых расстояниях, но они переплетаются таким сложным образом, что это очень трудно нарисовать.
Какую бы форму не принимали свернутые дополнительные измерения, и сколько бы их не было, в каждой точке вдоль бесконечных измерений будет находиться маленькое компактное пространство, содержащее в себе все свернутые измерения. Поэтому, если теоретики, занимающиеся струнами, правы, то везде в видимом пространстве — на кончике вашего носа, на северном полюсе Венеры, в точке на теннисном корте, куда вы послали ракеткой мяч во время последней подачи, — должно находиться шестимерное многообразие Калаби — Яу невидимого крохотного размера. В каждой точке пространства должна присутствовать многомерная геометрия.
Теоретики, занимающиеся струнами, часто предполагают, как это уже сделал Клейн, что свернутые измерения имеют размеры, равные планковской длине 10-33 см. Компактные измерения планковских размеров были бы необычайно хорошо спрятаны. Почти наверняка у нас нет способов обнаружить нечто столь малое. Поэтому весьма вероятно, что дополнительные измерения планковских размеров не оставляют никаких видимых следов своего существования. Следовательно, даже если мы живем во вселенной с дополнительными измерениями планковских размеров, мы будем регистрировать только три обычных измерения. Вселенная может иметь много таких крохотных измерений, но может статься, что мы никогда не достигнем достаточной разрешающей способности, чтобы их обнаружить.
Ньютоновский закон для силы тяготения при наличии дополнительных измерений
Хорошо иметь наглядное, описательное объяснение того, почему дополнительные измерения прячутся после компактификации или сворачивания до очень маленьких размеров. Но не мешало бы проверить, что законы физики согласуются с этими интуитивными представлениями.
Посмотрим на ньютоновский закон для силы тяготения, который в законченном виде был предложен Ньютоном в XVII веке. Этот закон говорит нам, каким образом сила тяготения зависит от расстояния между двумя массивными телами[22]. Закон Ньютона известен как закон обратных квадратов, означающий, что сила тяготения уменьшается с расстоянием обратно пропорционально квадрату расстояния. Например, если вы удвоите расстояние между двумя телами, сила их гравитационного притяжения уменьшится в четыре раза. Если расстояние между телами увеличивается в три раза по сравнению с первоначальным, гравитационное притяжение уменьшается в девять раз. Закон обратных квадратов для тяготения является старейшим и самым важным из законов физики. Среди прочего, этот закон объясняет движение планет по тем орбитам, которые мы видим. Любая жизнеспособная физическая теория тяготения должна воспроизводить закон обратных квадратов, или она будет обречена на провал.
Тот вид зависимости силы тяготения от расстояния, который заложен в ньютоновском законе обратных квадратов, тесно связан с числом пространственных измерений. Причина этого в том, что число измерений определяет, насколько быстро рассеивается гравитация при распространении в пространстве.
Подумаем над этой связью, что очень пригодится нам позднее, когда мы будем рассматривать дополнительные измерения. Для этого представив себе водопровод, вода из которого может быть направлена через шланг или через разбрызгиватель. Предположим, что через шланг и через разбрызгиватель протекает одинаковое количество воды и этой водой нужно полить определенный цветок в саду (рис. 20). Когда вода идет по шлангу, направленному на цветок, этот цветок получит всю воду. Расстояние от начала шланга до насадки, направленной на цветок, несущественно, так как вся вода должна в конце концов дойти до цветка независимо от того, насколько далеко находится шланг.
Теперь представим, что то же количество воды пропускается через разбрызгиватель, который одновременно поливает много цветков. Иначе говоря, разбрызгиватель подает воду по окружности, так что она попадает на все цветки, находящиеся на определенном расстоянии. Так как теперь вода распределяется среди всего, что есть на данном расстоянии, выбранный цветок будет получать не всю воду. Более того, чем дальше цветок от источника, тем больше растений будет поливать разбрызгиватель, и вода будет распределена по большей территории (рис. 21). Это произойдет потому, что вы можете полить больше растений на окружности длиной в три метра, чем на окружности длиной в один метр. Поскольку вода разбрызгивается шире, более далекий цветок получает меньше воды.
Аналогично, все, что равномерно распределяется более чем в одном направлении, будет оказывать меньшее влияние на любую конкретную вещь, находящуюся на большем расстоянии, будь это цветок или, как мы вскоре увидим, тело, на которое действует сила тяготения. Гравитация, как вода, чем дальше, тем шире распределяется.
Этот пример позволяет также увидеть, почему распределение так сильно зависит от числа измерений, в которых распространяется вода (или тяготение).
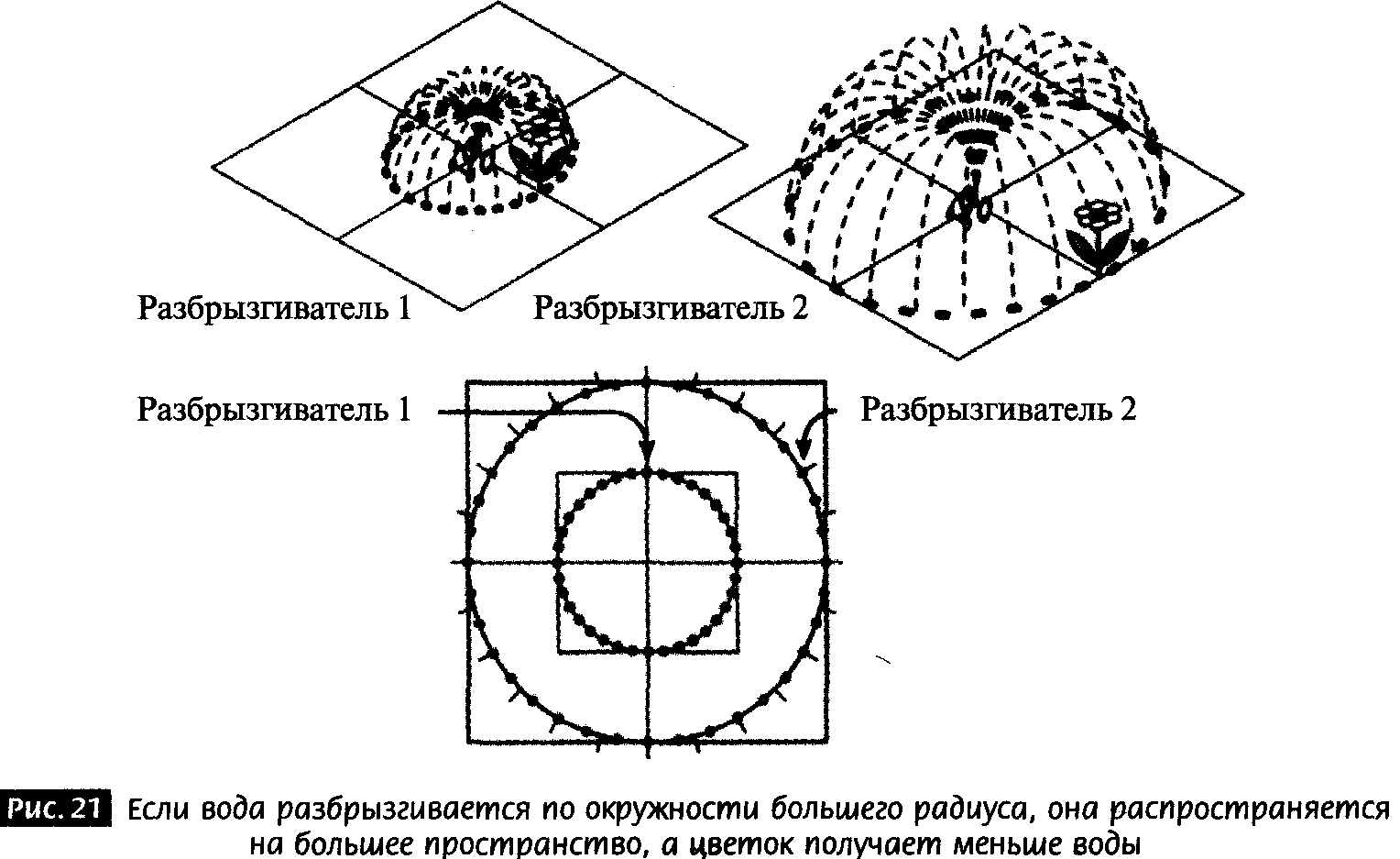

Вода из двумерного разбрызгивателя рассеивается с увеличением расстояния, в отличие от воды из одномерного шланга, которая вообще не рассеивается. Представьте теперь разбрызгиватель, распределяющий воду по поверхности сферы, а не только по окружности. (Такой разбрызгиватель напоминал бы нечто вроде созревшего одуванчика.) В этом случае вода будет рассеиваться с расстоянием значительно быстрее.
Применим эти рассуждения к тяготению и выведем точную зависимость от расстояния силы тяготения в трех измерениях. Закон тяготения Ньютона вытекает из двух следующих фактов: тяготение действует одинаково по всем направлениям, а пространство трехмерно. Представим планету, притягивающую любую находящуюся поблизости массу. Так как сила тяготения одинакова по всем направлениям, интенсивность гравитационного притяжения, оказываемого планетой на другое массивное тело, например луну, будет зависеть не от направления, а от расстояния между телами.
Чтобы графически изобразить интенсивность гравитационной силы, слева на рис. 22 показаны радиальные линии, выходящие наружу из центра планеты и напоминающие струи воды, летящие из разбрызгивателя. Плотность этих линий определяет интенсивность гравитационного притяжения, оказываемого планетой на все, что ее окружает. Если тело пронизывает большее количество силовых линий, это будет означать большее гравитационное притяжение, меньшее количество силовых линий будет означать меньшее гравитационное притяжение.
Заметим, что сферическую оболочку, нарисованную на любом расстоянии независимо от того, далеко она или близко от центра, пересекает одно и то же число силовых линий (центральный и правый рисунки на рис. 22). Число силовых линий никогда не меняется. Но так как силовые линии распределены по всем точкам поверхности сферы, сила на большем расстоянии неизбежно меньше. Точный коэффициент ослабления определяется количественной мерой того, насколько широко расставлены силовые линии на любом заданном расстоянии.
На любом расстоянии от массы через сферическую поверхность проходит фиксированное число силовых линий. Площадь этой сферической поверхности пропорциональна квадрату ее радиуса, т. е. равна некоторому числу, умноженному на квадрат радиуса. Так как по поверхности сферы распределено фиксированное число гравитационных силовых линий, сила тяготения должна уменьшаться обратно пропорционально квадрату радиуса. Это распределение гравитационного поля и есть причина закона обратных квадратов для тяготения.
Закон Ньютона в случае компактных измерений
Итак, теперь мы знаем, что в трех измерениях тяготение должно подчиняться закону обратных квадратов. Обратим внимание, что доказательство, как кажется, критически зависит от того факта, что существуют три пространственных измерения. Если бы было только два измерения, тяготение распространялось бы только по окружности, и сила тяготения уменьшалась бы не так сильно с расстоянием. Если число измерений было бы больше трех, площадь поверхности гиперсферы росла бы значительно быстрее с ростом расстояния между планетой и ее луной, так что сила убывала бы значительно быстрее. Похоже, что только три пространственных измерения приводят к зависимости от расстояния в виде закона обратных квадратов. Но если это так, как могут теории с дополнительными измерениями требовать выполнения ньютоновского закона обратных квадратов для тяготения?
Очень интересно видеть, каким образом компактифицированные измерения разрешают этот потенциальный конфликт. Суть рассуждений состоит в том, что силовые линии не могут распространяться на произвольное расстояние по компактным измерениям, так как они имеют конечный размер. Хотя силовые линии изначально расходятся по всем измерениям, после того, как они выйдут за пределы размеров дополнительных измерений, им не останется ничего иного, кроме как распространяться в направлениях бесконечных измерений.
Это опять может быть проиллюстрировано примером со шлангом. Представьте, что вода поступает в шланг через маленький прокол в крышке, прикрывающей конец шланга (рис. 23). Устремившаяся через прокол вода не сразу потечет вдоль по шлангу, а сначала распределится по всему сечению трубки. Тем не менее, поливая наш цветок из другого конца шланга, мы ясно понимаем, что способ, каким вода поступает в шланг, не имеет для нас никакого значения. Хотя вода и распределится вначале по более чем одному направлению, она быстро достигнет внутренней поверхности шланга и потечет далее так, как будто существует только одно направление. По существу, именно это происходит с гравитационными силовыми линиями в малых компактифицированных измерениях.
Как и ранее, можно вообразить фиксированное число силовых линий, идущих от массивного шара. На расстояниях, меньших размеров дополнительных измерений, эти силовые линии распространяются равномерно во всех направлениях. Если бы вы могли измерить тяготение на этом малом масштабе, вы бы получили следствия многомерной гравитации. Силовые линии распространялись бы так же, как вода, поступающая в шланг через прокол и распределяющаяся по внутренней части шланга.


Однако на расстояниях больших, чем размеры дополнительных измерений, силовые линии могут распространяться только по бесконечным направлениям (рис. 24). В малых компактных измерениях силовые линии наткнутся на край пространства, так что они не смогут распространяться по этому пути дальше. Они должны искривиться, и единственный оставшийся для них путь — двигаться в направлении больших измерений. Поэтому на расстояниях, больших, чем размеры дополнительных измерений, все выглядит так, как будто дополнительных измерений нет, и закон силы превращается в ньютоновский закон обратных квадратов, который мы и наблюдаем. Это означает, что даже с качественной точки зрения вы не можете знать о существовании дополнительных измерений, если измеряете гравитационную силу только между телами, расстояние между которыми больше размера свернутого измерения. Зависимость от расстояния отражает существование дополнительных измерений только в крохотной области внутри компактного пространства.
О других способах ограничить измерения
Теперь мы установили, что когда дополнительные измерения достаточно малы, они невидимы, и отсутствуют какие-либо измеримые следствия их существования в масштабах длин, которые мы наблюдаем. В течение долгого времени теоретики-струнники предполагали, что дополнительные измерения — это измерения, имеющие планковскую длину, однако недавно некоторые из нас поставили это предположение под вопрос.
Никто не понимает теорию струн настолько хорошо, чтобы с определенностью сказать, какие размеры окажутся у дополнительных измерений. Возможны размеры, сравнимые с планковской длиной, но и любое измерение, слишком маленькое для того, чтобы его можно было увидеть, тоже допустимо. Планковская длина настолько мала, что даже значительно большие Свернутые измерения могут ускользнуть от наблюдения. Важный вопрос при изучении дополнительных измерений состоит в том, насколько велики могут быть эти измерения, если допустить, что мы их до сих пор не видели.
Среди вопросов, обсуждаемых в этой книге, есть и вопросы о том, насколько велики могут быть дополнительные измерения, приводят ли эти измерения к каким-либо заметным явлениям в мире элементарных частиц и как это можно экспериментально исследовать. Мы увидим, что существование дополнительных измерений может существенно изменить правила, по которым мы изучаем физику частиц, и, более того, некоторые из этих изменений могут привести к экспериментально наблюдаемым следствиям.
Еще более радикальный вопрос, который мы исследуем, состоит в том, должны ли дополнительные измерения быть малыми. Мы не видим крохотных измерений, но обязаны ли измерения быть маленькими для того, чтобы быть невидимыми? Может ли дополнительное измерение простираться бесконечно, но так, чтобы мы его не видели? Если такое возможно, то дополнительные измерения будут сильно отличаться от тех измерений, которые мы рассматривали. Пока что я нашла только простейшую возможность. Позднее мы увидим, почему даже такое радикальное предположение о бесконечном дополнительном измерении не может быть исключено, если оно существенно отличается от трех привычных нам бесконечных измерений.
В следующей главе будет рассмотрен еще один вопрос, который мог у вас возникнуть: почему малые дополнительные измерения не могут быть просто отрезками, не свернутыми в шарик, а просто ограниченными двумя «стенками»? Такая возможность не приходит в голову сразу, но почему нет? Ответ состоит в том, что идея о конце пространства подразумевает знание того, что там происходит. Испытывает ли все на краю вселенной резкий обрыв, как, по-видимому, следует из старых картин плоской Земли? Или все отражается обратно? Или туда никогда нельзя попасть? Необходимость уточнения того, что происходит на краю, означает, что вы должны знать то, что ученые называют граничными условиями. Если пространство кончается, то где это происходит и на чем все кончается?
Браны — мембраноподобные объекты в многомерном пространстве — обеспечивают необходимые граничные условия для миров, которые «кончаются». Как мы увидим в следующей главе, браны могут сделать мир (или много миров) разнообразными.
Глава 3
Исключительные пассажи: браны, миры на бранах и балк
I’m gonna stick like glue,
Stick, because I’m stuck on you.
Elvis Presley[23]
В противоположность трудолюбивой Афине, Икар редко читал книги. Чаще всего он предпочитал компьютерные игры и возню со всякими техническими приспособлениями и автомобилями. Но Икар не выносил ездить в Бостон, где водители были неосторожны, дороги плохо размечены, а все шоссе непрерывно находились в состоянии ремонта, каждая поездка Икара заканчивалась тем, что он застревал в пробке, что особенно его расстраивало, когда он видел над головой свободную дорогу по воздуху. Она манила Икара, но у него не было возможности быстро до нее добраться, так как не в пример совам Афины он не мог летать. Для Икара, застрявшего в бостонских пробках, третье измерение было вообще ни к чему.
Еще совсем недавно очень мало уважающих себя физиков считали, что дополнительные измерения заслуживают того, чтобы об них думать. Эти измерения были слишком умозрительны и слишком незнакомы — никто не мог сказать о них что-то определенное. Однако в последние годы судьба улыбнулась дополнительным измерениям. Их перестали избегать, как нежелательных незваных гостей, они превратились в очень популярную, стимулирующую размышления деятельность. Вновь обретенная респектабельность обязана своим происхождением бранам и тем поистине новым теоретическим возможностям, которые возникли благодаря этим поразительным конструкциям.
Браны ворвались в физическое сообщество, как ураган, в 1995 году, когда физик Джо Полчинский из Института теоретической физики Кавли в Санта-Барбаре установил, что они важны для теории струн. Но даже до этого физики предлагали браноподобные объекты. Одним таким примером была р-брана, объект, который простирается бесконечно далеко только в нескольких измерениях и который был математически выведен физиками с помощью эйнштейновской общей теории относительности. Физики, занимающиеся частицами, также предлагали механизмы удержания частиц на браноподобных поверхностях[24]. Однако браны в теории струн были первым известным типом бран, который может удерживать не только частицы, но и силы, и вскоре мы увидим, что это — часть тех свойств, которые делают браны столь интересными. Как Икар, застрявший на двумерной дороге в трехмерном пространстве, частицы и силы могут быть захвачены на поверхностях меньшего числа измерений, называемых бранами, даже если у вселенной есть еще много других измерений. Если теория струн правильно описывает мир, в котором мы живем, у физиков не остается иного выбора кроме признания потенциальной возможности существования таких бран.
Мир бран — это волнующий новый ландшафт, который произвел революцию в нашем понимании тяготения, физики частиц и космологии. Браны могут реально существовать в космосе, и нет никаких убедительных причин отрицать, что мы могли бы жить на одной из них. Браны могут даже играть важную роль в определении физических свойств нашей Вселенной и окончательного объяснения наблюдаемых явлений. Если это так, то браны и дополнительные измерения должны присутствовать в теории.
Браны как слои
В гл. 1 мы рассмотрели способ рассмотрения двумерного мира Флатландии как двумерного слоя трехмерного пространства. Герой книги Эбботта Э. Квадрат совершил путешествие за пределы двумерной Флатландии в третье измерение и заметил, что Флатландия была всего лишь слоем большего трехмерного мира.
После своего возвращения Э. Квадрат рассудил, кстати, вполне логично, что увиденный им трехмерный мир также есть не что иное как опять-таки слой — трехмерный слой пространства еще большего числа измерений. Под «слоем» я понимаю не просто двумерную мембрану толщиной как у листа бумаги, но логическое расширение подобного понятия, если угодно, обобщенную мембрану. Предложенные Э. Квадратом трехмерные слои можно понимать как трехмерные ломти в четырехмерном пространстве.
Но его трехмерный спутник решительно оборвал рассуждения Э. Квадрата на тему трехмерных слоев. Как почти любой из известных нам людей, этот лишенный воображения обитатель трех измерений верил только в те три измерения пространства, которые он видел. Он не мог даже представить четвертое измерение.
Благодаря бранам в физику проникли математические понятия, похожие на те, которые были более века назад описаны во «Флатландии». Физики вернулись к идее, что окружающий нас трехмерный мир может быть трехмерным слоем мира с большим числом измерений. Брана — это определенная область пространства-времени, простирающаяся только по (возможно, многомерному) слою пространства. Слово «мембрана» поясняет выбор слова «брана», так как мембраны, как и браны, являются слоями, которые либо окружают, либо прорезают субстанцию. Некоторые браны являются «слоями» внутри пространства, другие представляют собой «слои», охватывающие пространство, как ломти хлеба в сандвиче.
Так или иначе, брана есть область, имеющая меньшее число измерений, чем полное многомерное пространство, которое ее окружает или ограничивает. Заметим, что мембраны имеют два измерения, а браны могут иметь любое число измерений. Хотя наибольший интерес для нас будут представлять браны с тремя пространственными измерениями, само слово «брана» будет относиться ко всем «слоям» такого типа. Некоторые браны имеют три пространственных измерения, но другие браны могут иметь большее (или меньшее) число измерений.
Мы будем пользоваться словом 3-браны, имея в виду браны в трех измерениях, словом А-браны для бран в четырех измерениях и т. д.
Граничные браны и вложенные браны
В гл. 1 я уже объяснила, почему дополнительные измерения могут быть не видны. Они могут быть свернуты в столь маленькие комочки, что никогда не возникнет никаких свидетельств их существования. Ключевой момент состоит в том, что дополнительные измерения должны быть малы. Но ни одна из причин не основана на том, что измерения свернуты.
Отсюда вытекает альтернативная возможность: может быть, измерения не свернуты, а просто обрываются на конечном расстоянии. Так как понятие об измерениях, ведущих в никуда, потенциально опасно — никому не хотелось бы, чтобы какие-то области вселенной внезапно резко обрывались, — у конечных измерений должны существовать границы, которые определяют, где и как им заканчиваться. Вопрос состоит в том, что происходит с частицами и энергией, когда они достигают этих границ?
Ответ состоит в том, что они наталкиваются на брану. В многомерном мире браны являются границами полного многомерного пространства, называемого балком[25]. В противоположность бране, балк распространяется по всем направлениям. Он заполняет каждое измерение, как на бране, так и вне браны (рис. 25). Поэтому балк «объемен», в то время как брана плоская (в некоторых измерениях), как блин. Если браны ограничивают балк в некоторых измерениях, часть измерений балка должны быть параллельными бране, а другие измерения должны на ней начинаться. Если брана есть граница, то измерения, начинающиеся на бране, должны простираться только в одну сторону.

Чтобы понять природу конечных измерений, кончающихся на бране, рассмотрим очень длинную тонкую трубку. Трубка имеет три измерения: одно длинное и два коротких. Чтобы сделать аналогию с плоскими бранами максимально наглядной, представим, что наша трубка имеет квадратное сечение. Бесконечно длинная трубка такого типа будет иметь четыре бесконечно длинных прямых стенки. Если считать, что трубка сама по себе является вселенной, то она будет трехмерной, причем два измерения ограничены с каждой стороны стенками, а одно простирается бесконечно далеко.
Мы знаем, что если разглядывать длинную тонкую трубку издали (или с недостаточным разрешением), она выглядит одномерной, очень похожей на садовый шланг из предыдущей главы. Но можно также спросить, как это мы сделали в случае вселенной садового шланга, как будет выглядеть вселенная трубки (состоящая из самой трубки и ее внутренней части) с точки зрения живущего внутри разумного существа.
Как вы можете предположить, это будет зависеть от разрешающей способности разумного существа. Маленькая муха, способная передвигаться внутри квадратной трубки, будет считать эту трубку трехмерной. Мы предполагаем, что в противоположность примеру с двумерным садовым шлангом, муха может двигаться не только по поверхности, но и внутри трубки. Тем не менее, как и в случае с садовым шлангом, муха будет воспринимать длинное измерение иначе, чем два коротких. В одном направлении муха может улететь сколь угодно далеко (если считать, что трубка очень длинная или бесконечная), в то время как по другим двум направлениям она может пролететь очень короткое расстояние, равное ширине трубки.
Однако между вселенной садового шланга и вселенной трубки есть разница, связанная не только с числом измерений у каждой из них. В противоположность жуку из предыдущей главы, муха в трубке перемещается внутри нее. Поэтому муха иногда наталкивается на стенки. Она может двигаться вперед и назад или вверх и вниз, натыкаясь при этом на границу. С другой стороны, жук на шланге никогда не достигнет такой границы, а вместо этого будет ползать и ползать кругом.
Когда муха достигает границы своей вселенной-трубки, ее поведение должно управляться определенными правилами. Это поведение определяют стенки трубки. Муха может удариться в стенку и сесть на нее, или трубка может быть отражающей, так что муха отскочит после удара о стенку. Если бы трубка была реальной вселенной, ограниченной бранами, то эти двумерные браны определяли бы, что произойдет, когда их достигает частица или что-то другое, способное переносить энергию.
Когда предметы достигают граничной браны, они отскакивают назад, в точности как бильярдные шары отскакивают от краев стола или свет отражается от зеркала. Это пример того, что физики называют отражательным граничным условием. Если предметы отскакивают от браны, энергия не теряется, она не поглощается бранами и не утекает. За бранами ничего нет. Граничные браны — это «концы мира».
В многомерной вселенной браны играют роль граничных стенок в рассмотренном выше примере вселенной-трубки. Как и стенки, такие браны будут иметь меньшее число измерений, чем полное пространство: граница всегда имеет меньше измерений, чем объект, который она ограничивает. Это так же верно для границ пространства, как и для корочки, являющейся границей буханки хлеба. Это также верно для стен вашего дома, имеющих на одно измерение меньше, чем комната, которую они окружают: комната трехмерна, в то время как любая отдельная стена (при условии, что мы пренебрегаем ее толщиной) простирается только в двух измерениях.
Хотя до сих пор в этом разделе я обсуждала браны, расположенные на границах, эти браны необязательно должны находиться на краю балка. В частности, браны могут располагаться вдали от границы, внутри пространства. Если граничная брана напоминает тонкую корочку на буханке хлеба, то не являющаяся граничной брана будет похожа на тонкий слой хлеба внутри буханки. Не являющаяся граничной брана все еще будет объектом с меньшим числом измерений, как те, которые мы уже рассматривали. Однако не-граничная брана будет с каждой стороны окружена балком большего числа измерений.
В следующем разделе мы увидим, что вне зависимости от того, чему равно число измерений балка или браны, а также независимо от того, находятся ли браны внутри пространства или на его границе, браны могут задерживать частицы и взаимодействия между ними. В результате область пространства, которую они занимают, оказывается весьма необычной.
Захваченные бранами
Весьма маловероятно, что вы побывали во всех доступных частях света. Скорее всего, есть места, которые вы хотели бы посетить, и вы мечтаете о путешествиях, которые никогда не совершите, например в космос или на дно океана. Вы не были в этих местах, но, в принципе, могли бы там быть. Не существует физических законов, запрещающих это.
Однако, если бы вы жили внутри черной дыры, ваши возможности путешествовать были бы очень сильно ограничены, даже сильнее, чем у женщин Саудовской Аравии. Черная дыра (пока она не распадется) удерживала бы вас (или, скорее, ваши искалеченные черной дырой останки) внутри, и вы никогда не могли бы выбраться оттуда.
Имеется множество примеров более знакомых предметов с ограниченной свободой передвижения, для которых действительно недоступны некоторые области пространства. Заряд на проволоке и бусинка на счетах — оба эти предмета существуют в трехмерном мире, однако двигаются только в одном из его измерений. Существуют и хорошо знакомые предметы, ограниченные двумерными поверхностями. Капли воды на занавеске в ванной комнате перемещаются только вдоль двумерной поверхности (рис. 26). Бактерия, помещенная между предметными стеклами микроскопа, также испытывает только двумерное движение. Еще одним примером может служить игра «Пятнадцать» Сэма Ллойда, надоедливая игрушка, состоящая из маленькой пластмассовой коробочки, заполненной передвигающимися квадратными пластинками с буквами, которые вы должны перемещать до тех пор, пока они не соберутся в какую-то фразу (рис. 27). Если вы не жульничаете, то буквы остаются внутри пластмассовой коробочки; они никогда не могут передвигаться в третьем измерении.
Как занавески в ванной или игра Ллойда, браны удерживают предметы на поверхностях меньшего числа измерений. Они открывают возможность того, что в мире с дополнительными измерениями не вся материя может перемещаться где угодно. Точно так же, как капли воды на занавеске ограничены двумерной поверхностью, частицы или струны могут быть привязаны к трехмерной бране, сидящей внутри многомерного мира. Однако, в противоположность каплям на занавеске, они действительно находятся в западне. И, в противоположность игре «Пятнадцать», браны не произвольны. Они являются естественными игроками в многомерном мире.
Захваченные бранами частицы находятся в настоящем плену у этих бран благодаря законам физики. Связанные бранами объекты никогда не отваживаются перейти в дополнительные измерения, окружающие брану. Браны захватывают в плен не все частицы; некоторые частицы могут свободно перемещаться по всему балку. Но то, что отличает теории с бранами от многомерных теорий без бран, — это присутствие частиц на бранах, которые не способны перемещаться по всем направлениям.
В принципе, браны и балк могут иметь любое число измерений, с той разницей, что брана никогда не может иметь больше измерений, чем балк. Размерность браны — это число измерений, в которых дозволено перемещаться захваченной браной частице. Хотя имеется много возможностей, наиболее интересными для нас в дальнейшем будут трехмерные браны. Мы не знаем, почему три измерения как-то специально выделены. Но браны с тремя пространственными измерениями могут иметь отношение к нашему реальному миру, так как они могут простираться по известным нам трем пространственным измерениям. Такие браны могут возникать в балке с любым числом измерений, большим, чем три, например, четырьмя, пятью или больше измерениями.
Даже если Вселенная действительно имеет много измерений, и знакомые нам частицы и силы захвачены простирающейся в трех измерениях браной, они будут продолжать вести себя так, как будто живут только в трех измерениях. Захваченные бранами частицы будут перемещаться только по бране. И если на брану упадет свет, его лучи будут распространяться только по бране. На трехмерной бране свет будет вести себя в точности так же, как в реальной трехмерной Вселенной.
Кроме того, захваченные бранами силы оказывают влияние только на частицы, захваченные той же браной. Вещество, из которого мы состоим, — ядра и электроны — и силы, с которыми взаимодействуют эти строительные блоки, например электрические силы, должны быть заключены на трехмерной бране. Связанные бранами силы будут распространяться только вдоль своей браны, а захваченные бранами частицы будут обмениваться и перемещаться только вдоль измерений браны.
Таким образом, если вы живете на такой трехмерной бране, вы можете свободно перемещаться по ее измерениям, так же как вы это сейчас делаете в трех измерениях. Все захваченное трехмерной браной будет выглядеть совершенно так же, как это выглядело бы, если бы мир был действительно трехмерным. Другие измерения будут существовать по соседству с браной, но все, что прилипло к трехмерной бране, никогда не сможет проникнуть в балк с большим числом измерений.
Однако, хотя силы и материя могут быть приклеены к бране, миры бран, как мы знаем, интересны именно потому, что не все захватывается единственной браной. Например, гравитация никогда не захватывается браной. Согласно общей теории относительности, гравитация неразрывно сплетена со структурой пространства и времени. Это означает, что гравитация должна действовать во всем пространстве и в любом измерении. Если бы она могла быть привязана к единственной бране, мы были бы вынуждены отвергнуть общую теорию относительности.
К счастью, это не так. Даже если браны существуют, гравитация будет ощущаться везде, на бранах и вне них. Это важно, так как означает, что миры на бранах должны взаимодействовать с балком, пусть даже только через гравитацию. Так как гравитация проникает в балк, и все взаимодействует через гравитацию, миры на бранах будут всегда связаны с дополнительными измерениями. Миры на бранах не существуют в изоляции, они есть часть большего целого, с которым они взаимодействуют. В дополнение к гравитации, в балке, возможно, существуют другие частицы и силы. Если это так, то подобные частицы могут также взаимодействовать с частицами, захваченными браной, и связывать сидящие на бране частицы с балком большей размерности.
Браны, возникающие в теории струн, которые мы кратко рассмотрим ниже, обладают, помимо упомянутых свойств, специфическими свойствами: они могут обладать особыми зарядами и особым образом откликаться, если их толкнуть. Однако ниже, говоря о бранах, я буду редко обращаться к таким детальным свойствам. Достаточно знать те свойства, которые мы рассмотрели в этой главе: браны — это поверхности меньшего числа измерений, которые могут быть прибежищем частиц и сил и являться границами пространства с большим числом измерений.
Миры на бранах: эскиз шведской стенки из бран
Так как браны могут захватывать большинство частиц и сил, то вполне вероятно, что Вселенная, в которой мы живем, может размещаться на трехмерной бране, плавающей в море дополнительных измерений. Гравитация будет простираться и в дополнительные измерения, но звезды, планеты, люди и все прочее, что мы ощущаем, может находиться в заточении на трехмерной бране. В этом случае мы бы жили на бране. Брана могла бы быть нашей естественной средой обитания. Понятие о мире на бране основано на этом предположении (рис. 28).
Если может существовать одна брана, висящая в пространстве-времени большего числа измерений, то ничто не препятствует возможности существования

многих других бран. В сценарии мира бран часто рассматривают не только одну-единственную брану. До сих пор мы не знаем, сколько бран или их типов может существовать в космосе. Теории, рассматривающие более чем одну брану, иногда называют теориями мультивселенной (рис. 29). Часто это слово используется для описания космоса, состоящего из невзаимодействующих или только слабо взаимодействующих частей.
Термин «мультивселенная» кажется мне несколько странным, так как Вселенная, по определению, есть целое, представляющее единство своих частей. Однако возможно, что существуют различные браны, находящиеся на слишком большом расстоянии друг от друга, чтобы сообщаться между собой, или способные сообщаться друг с другом очень слабо, за счет обмена движущимися между ними частицами. Тогда частицы на далеких бранах будут испытывать совершенно разные силы, и прикрепленные к бране частицы никогда не будут иметь прямого контакта с частицами, прикрепленными к другой бране. Таким образом, когда существует более одной браны и они не имеют общих сил кроме тяготения, тогда я буду иногда называть приютившую их всех вселенную мультивселенной.
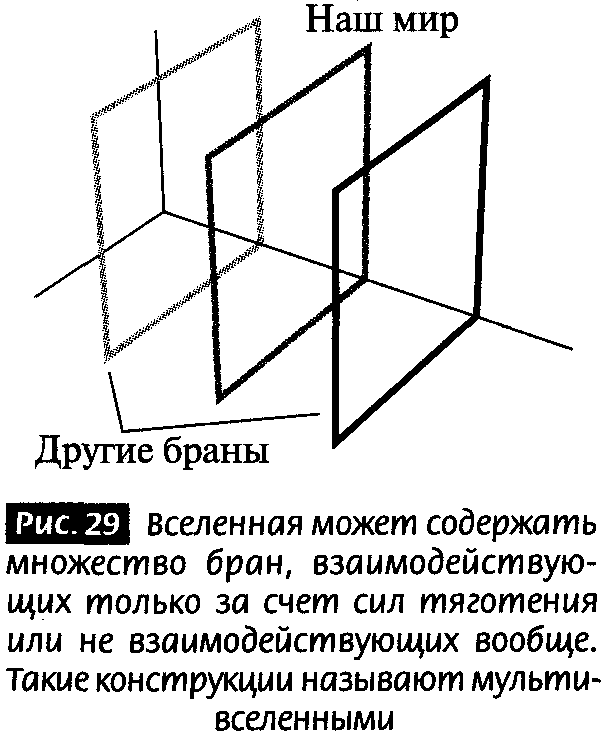
Размышления о бранах убеждают в том, что мы очень мало знаем о пространстве, в котором живем. Вселенная может быть величественной конструкцией, связывающей перемежающиеся браны. Даже если мы знаем все основные ингредиенты, в мультивселенной, содержащей более одной браны, становятся возможными экзотические новые сценарии геометрии пространства, а также мириады возможностей для распределения известных или неизвестных частиц на этих бранах. Имея на руках одну колоду карт, можно получить много разных вариантов сдач. Имеется множество возможностей.
Одни браны могут быть параллельными нашим и могут вмещать параллельные миры. Но может существовать и множество других типов миров. Браны могут пересекаться, и на пересечениях частицы могут попадать в ловушку. Браны могут иметь разные размерности. Они могут искривляться. Они могут двигаться. Они могут закручиваться вокруг невидимых измерений. Дайте волю своему воображению и нарисуйте любую картину, какая вам придет в голову, Не исключено, что в космосе существует и такая геометрия.
В мире, в котором браны погружены в балк большего числа измерений, могут существовать частицы, исследующие высшие измерения, и частицы, остающиеся в плену у бран. Если одна брана отделена от другой балком, то некоторые частицы могут находиться на первой бране, другие — на второй, а некоторые — посередине. Теории описывают много способов, которыми частицы и силы могут быть распределены по разным бранам и по балку. Даже для бран, выведенных из теории струн, мы до сих пор не знаем, почему эта теория должна выделять какое-то конкретное расположение частиц и сил. Миры бран предлагают новые физические сценарии, которые могут описывать одновременно тот мир, который, как мы считаем, нам известен, и другие миры, которые мы не знаем, находящиеся на других бранах, которых мы не знаем, и отделенные от нашего мира невидимыми измерениями.
Могут существовать новые силы, прикованные к удаленным бранам. По этим бранам могут распространяться частицы, с которыми мы никогда не будем непосредственно взаимодействовать. По разным бранам, а возможно, и по балку, может быть распределена дополнительная материя, дающая вклад в темную материю и темную энергию, — т. е. ту материю и энергию, о существовании которых мы догадываемся по их гравитационным эффектам, но природа которых остается загадкой. И гравитация может даже по-разному действовать на частицы при переходе с одной браны на другую.
Если на другой бране есть жизнь, находящиеся там существа, заключенные в совершенно другую окружающую среду, почти наверняка испытывают влияние других сил, которые регистрируются другими чувствами. Наши чувства настроены на восприятие окружающих нас химических веществ, света и звука. Так как фундаментальные силы и частицы, скорее всего, другие, существа на других бранах, если они существуют, вряд ли ведут жизнь, напоминающую жизнь на нашей бране. Другие браны, вероятно, совсем непохожи на нашу. Единственной общей силой является гравитация, но даже влияние гравитации может изменяться.
Следствия существования миров на бранах будут зависеть от числа и типов бран и от их местоположения. К сожалению для любознательного читателя, не требуется, чтобы на нас очень сильно влияли частицы и силы, закрепленные на далеких бранах. Они всего лишь могут определять, что движется в балке, и испускать слабые сигналы, которые даже могут никогда нас не достичь. Поэтому будет очень трудно детектировать многие из возможных миров на бранах, даже если они действительно существуют. Кроме того, единственным взаимодействием, про которое мы с уверенностью можем сказать, что оно осуществляется между материей на нашей бране и материей на любой другой бране, является гравитация, представляющая необычайно слабую силу. А без прямого свидетельства их существования, мы не сможем вывести браны из области теории и догадок.
Однако некоторые из миров на бранах, о которых я собираюсь рассказать, могут приводить к обнаружимым сигналам. К обнаруживаемым мирам на бранах относятся те, которые приводят к определенным следствиям для физических свойств нашего мира. И хотя разрастание возможного числа миров на бранах немного разочаровывает, эта идея необычайно захватывает. Браны не только могут помочь разрешить старые проблемы физики частиц, но если нам повезет, и один из сценариев, который я опишу ниже, окажется правильным, очень скоро свидетельства существования миров на бранах должны будут проявиться в экспериментах в физике элементарных частиц. Возможно, мы действительно живем на бране и узнаем об этом в течение ближайшего десятилетия.
В данный момент мы не знаем, какая (если хоть какая-нибудь) из многих возможностей является истинным описанием Вселенной. Поэтому я буду держать открытыми все возможности, с тем чтобы не упустить чего-то важного. Какой бы сценарий не оказался правильно описывающим наш мир, те сценарии, о которых я расскажу, предлагают новые захватывающие идеи, совсем недавно казавшиеся невозможными.
Глава 4
Подходы к проблемам теоретической физики
She’s a model and she’s looking good.
Kraftwerk[26]
— Привет, Афина! Ты что, смотришь «Касабланку»?
— Да. Не хочешь присоединиться? Сейчас как раз идет такая чудесная сцена.
You must remember this,
A kiss is just a kiss.
A sigh is just a sigh.
The fundamental things apply as time goes by[27].
— Подожди, Икар! не кажется ли тебе, что последняя строка немного странная? Казалось бы, она должна быть такой романтичной, но звучит так, как будто говорится о физике.
— Афина, если ты думаешь, что она странная, тогда тебе следует послушать первые строки песни:
This day and age we're living in
Give cause for apprehension,
With speed and new invention.
And things like fourth dimension,
Yet we get a trifle weary
With Mr. Einstein's theory…[28]
— Икар, неужели ты думаешь, что я тебе поверила? я знаю тебя, в следующий раз ты расскажешь мне про Рика и Илзу, сбежавших в седьмое измерение! Давай забудем, что я вообще что-то сказала, и просто посидим и посмотрим фильм?
Эйнштейн обнародовал общую теорию относительности в начале двадцатого века, а в 1931 году Руди Вэлли записал песню Германа Хупфелда, которую процитировал (кстати, правильно) Икар. Однако к тому времени, как Сэм напевал эту мелодию в фильме «Касабланка», слова, которые напомнил Икар, — так же как учение о пространстве-времени — были почти забыты массовой культурой. И хотя Теодор Калуца высказал свою идею о дополнительные измерениях в 1919 году[29], физики до недавнего времени совершенно не воспринимали эту идею серьезно.
Теперь, когда мы видели, что такое измерения и как они могут ускользнуть от нашего взора, мы почти готовы спросить, что вызвало этот новый интерес к дополнительным измерениям. Почему физики должны верить, что эти измерения действительно существуют в реальном физическом мире? Ответ на этот вопрос потребует значительно более продолжительных объяснений, включающих рассказ о некоторых наиболее значительных физических достижениях прошлого века. Прежде чем погрузиться в описание возможных вселенных с дополнительными измерениями, я в нескольких следующих главах дам обзор этих достижений и объясню, почему они являются предшественниками более современных теорий. Мы рассмотрим основные изменения во взглядах и понятиях, случившиеся в начале двадцатого века (квантовая механика, общая теория относительности), расскажем о сути современной физики частиц (Стандартная модель, симметрия, нарушение симметрии, проблема иерархии) и о новых идеях, подводящих к пока что нерешенным проблемам (суперсимметрия, теория струн, дополнительные измерения и браны).
Однако, прежде чем погрузиться в эти темы, мы совершим в этой главе краткое путешествие вглубь материи, чтобы оборудовать физическую сцену. И поскольку понимание того, где мы находимся, требует также некоторого знакомства с современными идеями, мы рассмотрим теоретические подходы, важные для современных исследований.
Сначала я думала, что «заниматься самым важным» — это разумный выбор правильной цитаты из песни. Но после некоторых размышлений слова стали звучать так похоже на физику, что я решила проверить, не сыграла ли моя память со мной шутку, как это часто бывает с текстами песен, даже в том случае, когда вы уверены, что они навсегда врезалась в вашу память. Я была удивлена (и позабавлена), когда обнаружила, что песня уходит корнями в физику больше, чем я могла вообразить. Я совершенно не понимала, что слова «время проходит» говорят о четвертом измерении.
Физическая интуиция может работать так же; из тоненьких нитей иногда могут образоваться неожиданные связи. Если вам повезет, то окажется, что вы нашли гораздо больше того, что искали, при условии, что вы искали в правильном месте. В физике, если вы обнаружили какие-то взаимосвязи, пусть и следуя неясным намекам, вы пытаетесь их расшифровать тем способом, который считаете наилучшим. Этот поиск может опираться на разумные оценки или на попытки вывести математические свойства теории, которой, как вы считаете, можно доверять.
В следующем разделе мы рассмотрим современные методы, используемые для поиска таких связей: построение моделей (мой конек) и альтернативный подход к фундаментальной физике высоких энергий — теорию струн. Теоретики, занимающиеся струнами (далее, для краткости, струнники — Прим. пер.), пытаются вывести универсальные предсказания из определенной теории, в то время как создатели моделей пытаются найти пути решения конкретных физических задач, а затем, опираясь на эти отправные точки, построить теории. Как создатели моделей, так и струнники занимаются поиском более всеобъемлющих теорий, обладающих большей предсказательной силой. Они стремятся ответить на сходные вопросы, но подходят к ним с разных сторон. Исследование иногда основывается на разумных оценках, как в случае построения моделей, иногда оно включает извлечение логических следствий из той окончательной теории, которая уже считается правильной, как в случае с подходом теории струн. Вскоре мы увидим, что современные исследования по дополнительным измерениям успешно соединяют элементы обоих методов.
Построение моделей
Хотя поначалу меня тянуло к математике и естественным наукам благодаря той определенности, которую они обещали, сейчас мне не менее интересны вопросы, на которые нет ответа, и связи, которым пока нет объяснений. Принципы, содержащиеся в квантовой механике, теории относительности и Стандартной модели, будят воображение, но они едва касаются тех примечательных идей, которыми увлечены сегодня физики. Мы чувствуем, что требуется что-то новое, ибо ощущаем недостаток идей. Эта нехватка является предвестником новых физических явлений, которые проявятся, когда мы осуществим новые эксперименты.
Ученые, занимающиеся физикой частиц (далее, для краткости, частичники — Прим. пер.), пытаются установить те законы природы, которые объясняют поведение элементарных частиц. Эти частицы и физические законы, которым они подчиняются, являются компонентами того, что физики называют теорией — определенным множеством элементов и принципов с правилами и уравнениями для предсказания того, как элементы взаимодействуют. Когда я говорю в этой книге о теориях, я буду использовать это слово в указанном смысле и не буду подразумевать «грубые рассуждения», как это делается на более разговорном языке.
В идеале физики мечтают найти теорию, способную объяснить все наблюдения, но использующую при этом самое малое возможное число правил и минимально возможное число фундаментальных ингредиентов. Конечной целью для ряда физиков является простая, элегантная, объединяющая теория, такая теория, которую можно использовать для предсказания результатов любого эксперимента в физике частиц.
Охота за такой объединяющей теорией — это честолюбивая, кто-то может сказать, дерзкая задача. В некотором отношении она отображает давно начавшиеся поиски простоты. В Древней Греции Платон рассматривал идеальные формы, подобные геометрическим фигурам и идеальным существам, которым только приближенно соответствуют земные тела. Аристотель также верил в идеальные формы, но он полагал, что только эксперименты могут обнаружить те идеалы, которых напоминают физические тела. Религии также часто постулируют более совершенное или более единое состояние, которое удалено от реальности, но как-то с ней связано. История изгнания из сада Эдема предполагает идеализированный предшествующий мир. Хотя вопросы и методы физики в наше время и у наших предков весьма отличаются друг от друга, физики тоже ищут более простую вселенную, и пытаются найти ее не в философии или религии, а в образующих наш мир фундаментальных составных частях.
Однако на пути поиска элегантной теории, которую мы можем связать с нашим миром, есть одно очевидное препятствие: когда мы глядим вокруг себя, мы видим очень мало той простоты, которую должна воплощать такая теория. Проблема состоит в том, что мир сложен. Требуется много усилий для того, чтобы связать простую, экономную формулировку с более сложным реальным миром. Помимо того, что единая теория должна быть простой и элегантной, она должна как-то вмещать достаточную структуру, чтобы соответствовать наблюдениям. Мы предпочитаем верить, что существует точка зрения, откуда все выглядит элегантно и предсказуемо. Однако Вселенная не является такой же чистой, простой и упорядоченной, как теории, с помощью которых мы надеемся ее описать.
Частичники преодолевают область, связывающую теорию с наблюдениями, с помощью двух различных методологий. Ряд теоретиков следует подходу «сверху вниз»: они стартуют с теории, которую считают правильной, например, теоретики-струнники начинают с теории струн и пытаются извлечь из нее следствия, так чтобы связать эту теорию со значительно более беспорядочным миром, который мы наблюдаем. С другой стороны, создатели моделей следуют подходу «снизу вверх»: они пытаются вывести лежащую в основе теорию, устанавливая связи между наблюдаемыми элементарными частицами и их взаимодействиями. Они ищут ключи к загадкам физических явлений и строят модели, приводящие к теориям, которые могут оказаться как верными, так и неверными. Оба подхода имеют свои достоинства и недостатки, и наилучший путь к успеху не всегда очевиден.
Конфликт между двумя научными подходами интересен тем, что он отражает два совершенно различных подхода к научным исследованиям. Это разделение представляет собой воплощение научных споров, идущих из глубины веков. Следуете ли вы платоновскому подходу, заключающемуся в стремлении понять нечто, исходя из более фундаментальной истины, или аристотелевскому подходу, основанному на эмпирических наблюдениях? Выбираете ли вы путь сверху вниз или путь снизу вверх?
Этот выбор можно также выразить словами «старый Эйнштейн против молодого Эйнштейна». В молодости Эйнштейн основывал свою работу на экспериментах и физической реальности. Даже его так называемые мысленные эксперименты базировались на физических ситуациях. Подход Эйнштейна изменился после того, как во время создания общей теории относительности он осознал ценность математики. Он обнаружил, что критическое значение для завершения его теории имели математические достижения, что побудило его в последующей деятельности к использованию более теоретических методов. Несмотря на успешное применение математики к общей теории относительности, дальнейшие математические поиски единой теории не привели Эйнштейна к успеху.
Как показывает работа Эйнштейна, есть различные типы научной истины и разные способы их поисков. Один способ основан на наблюдениях; именно так мы изучаем, например, квазары и пульсары. Другой основан на абстрактных принципах и логике; например, Карл Шварцшильд впервые вывел существование черных дыр как математическое следствие общей теории относительности. В конечном итоге мы хотели бы, чтобы оба способа сблизились, — сейчас существование черных дыр выводится как из математической обработки наблюдений, так и из чистой теории, однако на первых стадиях исследования наши успехи, основанные на двух типах истины, редко совпадают. В случае же теории струн принципы и уравнения по своей глубине и близко не стоят рядом с теми, на которых основана общая теория относительности, так что вывод следствий из этих принципов становится намного сложнее.
Когда теория струн впервые приобрела известность, она резко разделила мир физики частиц. Я была студенткой старшего курса в середине 1980-х годов, когда «струнная революция» впервые расколола мир физики частиц пополам. В это время одна часть физического сообщества с открытым сердцем решила посвятить себя неосязаемому математическому миру теории струн.
Основное исходное положение теории струн состоит в том, что струны, а не частицы являются самыми фундаментальными объектами в природе. Частицы, которые наблюдаются в окружающем нас мире, являются просто следствиями существования струн: они возникают из различных колебательных мод вибрирующей струны, что весьма напоминает то, как в результате колебаний скрипичной струны возникают различные музыкальные звуки. Теория струн завоевала признание, так как физики искали теорию, которая согласованным образом включает квантовую механику и общую теорию относительности и может делать предсказания вплоть до самых мельчайших доступных масштабов расстояний. Для многих теория струн выглядит как наиболее многообещающий кандидат на такую теорию.
Однако другая группа физиков решила сохранить контакт с миром относительно низких энергий, который можно исследовать экспериментально. Я была в Гарварде, и тамошние частичники, в том числе выдающиеся создатели моделей Говард Джорджи и Шелдон Глэшоу, а также многие талантливые аспиранты и студенты, остались стойкими приверженцами подхода, основанного на построении моделей, и продолжали исследования в этом направлении.
Вскоре развернулась ожесточенная борьба относительно достоинств двух противоположных точек зрения — теории струн и построения моделей, причем каждая сторона заявляла о более прочной позиции на пути к истине. Создатели моделей считали, что струнники находятся в математическом мире грез, в то время как струнники считали, что создатели моделей теряют свое время и игнорируют истину.
Так как в Гарварде было много блистательных создателей моделей и я получала удовольствие от этих идей, то, попав впервые в мир физики частиц, я примкнула к этому лагерю. Теория струн — волшебная теория, которая уже привела к глубоким математическим и физическим прорывам, и вполне может оказаться, что она содержит правильные составные части окончательного описания природы. Но поиск связи между теорией струн и реальным миром представляет устрашающую задачу. Проблема в том, что теория струн определена при значениях энергии, которые примерно в десять миллионов миллиардов раз больше, чем значения, которые мы способны экспериментально получать с помощью современных установок. Мы до сих пор даже не знаем, что случится, когда энергия ускорителей частиц увеличится всего в десять раз!
Колоссальная теоретическая пропасть отделяет теорию струн, в том виде, как мы ее сейчас понимаем, от предсказаний, описывающих наш мир. Уравнения теории струн описывают настолько ничтожно малые и обладающие такой невероятно большой энергией объекты, что любые сделанные на основе мыслимых технологий детекторы, которые мы только можем вообразить, не смогут даже увидеть эти объекты. Не только математически чудовищно трудно вывести следствия и предсказания теории струн, но даже не всегда ясно, как организовать составные части этой теории и определить, какую математическую задачу следует решать. Слишком легко потеряться в чаще деталей.
Теория струн может привести к избытку возможных предсказаний на расстояниях, которые мы действительно видим, — предсказываемые частицы зависят от до сих пор не определенной конфигурации фундаментальных составных частей теории. Без определенных гипотетических предположений теория струн выглядит так, будто в ней содержится больше частиц, больше взаимодействий и больше измерений, чем наблюдается в нашем мире. Нам нужно понять, что отсекает дополнительные частицы, взаимодействия и измерения от наблюдаемых. Мы до сих пор не знаем, существуют ли физические свойства, отделяющие одну конфигурацию от другой, и даже не представляем, как найти то единственное проявление теории струн, которое согласуется с нашим миром. Нам должно очень повезти, чтобы мы могли извлечь все правильные физические принципы, которые приведут к согласованию предсказаний теории струн с тем, что мы видим.
Например, невидимые дополнительные измерения теории струн должны отличаться от тех трех, которые мы видим. Гравитация в теории струн значительно сложнее, чем гравитация, которую мы наблюдаем вокруг нас и которая заставила яблоко упасть на голову Ньютону. Вместо этого гравитация в теории струн действует в шестимерном или семимерном пространстве с дополнительными измерениями. Какой бы пленительной и поразительной ни была теория струн, загадочные свойства вроде дополнительных измерений затеняют ее связь с видимой Вселенной. Что отличает эти дополнительные измерения от наблюдаемых? Почему не все они одинаковы? Открытие того, как и почему природа прячет дополнительные измерения теории струн, было бы ошеломляющим достижением, и ради него стоит исследовать все возможные способы, которые могли бы к этому привести.
До сих пор, однако, все попытки сделать теорию струн реалистичной напоминали косметическую хирургию. Для того чтобы согласовать предсказания этой теории с нашим миром, теоретики должны найти способ, как спокойно удалять частицы, сворачивать измерения и отбрасывать те куски, которых не должно остаться. Хотя окончательные наборы частиц соблазнительно близко приближаются к правильному набору, все же можно сказать, что эти наборы не совсем правильны. Признаком правильной теории должна также быть элегантность, но о красоте теории можно судить только после того, как мы полностью поймем все ее следствия. Теория струн сразу захватывает, но рано или поздно струнники должны задуматься над этими фундаментальными проблемами.
При изучении гористой местности без карты вам редко удается сказать, каким окажется самый прямой путь к вашей цели. На языке идей, как и в случае сложной местности, вначале совершенно неясно, по какому пути лучше всего идти. Даже если теория струн в конце концов объединяет все известные взаимодействия и частицы, мы до сих пор не знаем, содержит ли она единственный пик, представляющий конкретный набор частиц, сил и взаимодействий, или представляет более сложный ландшафт со многими возможными следствиями. Если бы дороги были ровными, с хорошо нанесенной разметкой, поиск пути был бы прост. Но вряд ли дело обстоит именно так.
Итак, подход к продвижению за пределы Стандартной модели, который я буду развивать, это построение моделей. Термин «модель» может пробудить воспоминания о маленькой модели корабля или замка, которые вы собирали в детстве. Или вы можете подумать о численном моделировании на компьютере, когда подразумевается воспроизведение известной динамики, например того, как растет народонаселение или как движется вода в океане. Моделирование в физике частиц не соответствует ни тому, ни другому из этих определений. Однако оно чем-то близко употреблению этого слова в журналах и на показах мод: модели, как на подиуме, так и в физике, представляют воображаемые творения и проявляются во множестве форм и образов. И все внимание достается самым красивым из них.
Нет нужды подчеркивать, что сходство на этом кончается. Модели физики частиц — это гипотезы об альтернативных физических теориях, которые могли бы лежать в основе Стандартной модели. Если вы представляете себе единую теорию как вершину горы, то создатели моделей — это первопроходцы, которые пытаются найти дорогу, связывающую вершину с находящимся внизу прочным основанием, состоящим из хорошо установленных физических теорий, дорогу, которая в конце концов свяжет вместе новые идеи. Хотя создатели моделей признают привлекательность теории струн и допускают возможность, что она когда-нибудь окажется правильной, они все-таки не так, как струнники, уверены в том, что знают, какую теорию они обнаружат, если когда-нибудь доберутся до вершины.
Как мы увидим в гл. 7, Стандартная модель есть определенная физическая теория с фиксированным числом частиц и сил, находящихся в четырехмерном мире. Модели, выходящие за рамки Стандартной, включают ее составные части и воспроизводят ее следствия при энергиях, которые уже были исследованы, но они содержат также новые силы, новые частицы и новые взаимодействия, которые можно обнаружить только на меньших расстояниях. Физики предлагают использовать эти модели для решения современных загадок. Модели могут предсказывать различные типы поведения для известных или предполагаемых частиц, которые определяются новым набором уравнений, вытекающих из гипотез модели. Они могут предлагать также новые пространственные декорации, вроде тех, которые мы использовали с дополнительными измерениями или бранами.
Даже когда мы полностью понимаем теорию и ее приложения, такую теорию можно применять разными способами, приводящими к различным физическим следствиям для реального мира, в котором мы живем. Например, даже если мы знаем, как и за счет каких сил в принципе взаимодействуют частицы, нам все равно нужно знать, какие конкретные частицы и силы существуют в реальном мире. Модели позволяют тестировать возможности.
Теории различаются по заложенным в них предположениям и физическим понятиям, например, по масштабам расстояний или энергий, на которых применимы принципы теории. Модели представляют способ проникновения в самую глубину таких отличительных свойств. Они позволяют использовать потенциальные приложения теории. Если вы рассматриваете теорию как общую инструкцию по выпечке кекса, то модель — это точный рецепт. Теория утверждает, что нужно добавить сахар, а модель уточняет, добавить ли полчашки или две чашки сахара. Теория утверждает, что изюм следует класть по вкусу, а модель предлагает вам быть благоразумными и не класть его совсем.
Создатели моделей рассматривают нерешенные задачи Стандартной модели и пытаются использовать известные теоретические инструменты для изучения ее проблемных мест. Такой подход основан на инстинктивном убеждении, что энергии, при которых теория струн дает определенные предсказания, слишком далеки от тех, которые мы можем наблюдать. Создатели моделей пытаются увидеть большую картину, чтобы суметь найти в ней кусочки, относящиеся к нашему миру.
Мы, создатели моделей, прагматично допускаем, что не можем получить все сразу. Вместо того чтобы пытаться вывести следствия теории струн, мы стараемся представить, какие компоненты лежащей в основе физической теории объясняют известные наблюдения и устанавливают связи между экспериментальными данными. Предположения модели могут оказаться частью окончательной фундаментальной теории, или они могут пролить свет на новые связи даже до того, как мы поймем их глубинные теоретические обоснования.
Физика всегда стремится предсказать как можно большее число физических величин, исходя из минимально возможного числа предположений, но это не означает, что нам всегда удается сразу же установить самые фундаментальные теории. Часто удается значительно продвинуться до того, как все становится понятным на самом фундаментальном уровне. Например, физики понимали понятия температуры и давления и использовали их в термодинамике и построении тепловых машин задолго до того, как удалось объяснить эти понятия на более фундаментальном микроскопическом уровне как результат случайного движения большого числа атомов и молекул.
Так как модели связаны с физическими «явлениями» (имеются в виду экспериментальные наблюдения), то создателей моделей, тесно связанных с экспериментом, иногда называют феноменологами. Однако «феноменология» — неудачный выбор термина. Он не отражает роли анализа данных, который в современном сложном научном мире глубоко встроен в теорию. Создание моделей намного теснее связано с интерпретацией и математическим анализом, чем может предложить феноменология в философском смысле этого слова.
Однако лучшие модели обладают бесценным свойством. Они дают определенные предсказания о физических явлениях, предоставляя экспериментаторам возможность подтвердить их или опровергнуть. Эксперименты при высоких энергиях — это не только поиск новых частиц, но и проверка моделей и поиск ключей к лучшим моделям. Каждая предложенная модель физики частиц включает новые физические принципы и новые физические законы, действующие при измеримых энергиях. Поэтому она предсказывает новые частицы и проверяемые связи между ними. Открытие таких частиц и измерение их свойств может подтвердить или опровергнуть предлагаемые идеи. Цель экспериментов при высоких энергиях состоит в том, чтобы пролить свет на лежащие в основе физические законы и ту концептуальную схему, которая придает этим законам предсказательную силу.
Только некоторые модели оказываются правильными, но модели — это лучший способ для исследования возможностей и построения хранилища конкурирующих вариантов. Если теория струн правильна, мы сможем в конце концов узнать, каким образом некоторые модели следуют из теории, так же как термодинамика вытекает их атомной теории. Однако в течение примерно десяти лет два сообщества физиков были резко разделены. Когда мы недавно обсуждали этот раскол с Альбионом Лоуренсом, молодым струнником из Университета Брандайса, он сказал: «Одна из трагедий состоит в том, что теория струн и создание моделей были различными видами интеллектуальной деятельности. Создатели моделей и струнники не разговаривали друг с другом годами. Я всегда думал о теории струн как о дедушке всех моделей».
Как струнники, так и создатели моделей ищут удобный, элегантный путь, связывающий теорию с наблюдаемым миром. Любая теория будет действительно неотразима и, возможно, правильна, только если весь этот путь, а не только взгляд с вершины, докажет свою элегантность. Создатели моделей, начинающие путь от подножия, рискуют многими фальстартами, но струнники, начинающие путь с вершины, рискуют обнаружить себя на краю крутого отдельно стоящего утеса, слишком удаленного от базового лагеря, чтобы можно было найти обратный путь домой.
Вы можете сказать, что все мы ищем язык Вселенной. Но в то время как струнники фокусируют внимание на внутренней логике грамматики, создатели моделей обращают внимание на существительные и те фразы, которые, по их мнению, наиболее полезны. Если бы физиков-частичников послали во Флоренцию изучать итальянский язык, то создатели моделей знали бы, как спросить про гостиницу, и приобрели бы словарь, чтобы ориентироваться в среде, но говорили бы они с забавным акцентом и никогда полностью не поняли бы «Ад». Струнники, напротив, увлеклись бы пониманием тонкостей итальянской литературы, но рисковали бы умереть от голода, прежде чем выучили, как спросить, где можно поесть!
К счастью, сейчас положение дел изменилось. В наши дни теория и феноменология поддерживают развитие друг друга, так что многие из нас одновременно размышляют о теории струн и экспериментально ориентированной физике. Я продолжаю в собственных работах следовать подходу построения моделей, но включаю также идеи из теории струн. Я думаю, что в конце концов успехи будут достигнуты путем сочетания лучшего из обоих методов.
Как говорит Альбион, «различия снова размываются, сосредоточившись по большей части в изучении дополнительных измерений. Люди опять разговаривают друг с другом». Группы теоретиков уже не так жестко определены, у них расширилась общая основа. Возникло новое сближение цели и идей. С научной и социальной точек зрения, сейчас имеется сильное пересечение между создателями моделей и струнниками.
Одной из замечательных сторон теорий с дополнительными измерениями, которые будут здесь описаны, является то, что при создании таких теорий идеи от обоих лагерей объединяются. Дополнительные измерения из теории струн могут оказаться помехой, но могут и привести к новым идеям для разрешения старых проблем. Мы, безусловно, можем спросить, где эти дополнительные измерения и почему мы их не видим. Но мы можем также спросить, могут ли эти невидимые измерения иметь какое-то значение в нашем мире. Эти измерения могут помочь объяснить лежащие в основе взаимосвязи, важные для наблюдаемых явлений. Создатели моделей получают удовольствие от сложной задачи привязывания понятий вроде дополнительных измерений к наблюдаемым величинам вроде соотношений между массами. И, если нам повезет, интуитивные прозрения, вдохновленные моделями с дополнительными измерениями, могут успешно разрешить одну из величайших проблем, с которой сталкивается теория струн, — ее экспериментальную недосягаемость. Создатели моделей использовали выведенные из теории струн теоретические элементы для атаки на проблемы физики частиц. И такие модели, включая модели с дополнительными измерениями, будут иметь проверяемые следствия.
Когда мы будем рассматривать модели с дополнительными измерениями, мы увидим, что модельный подход в соединении с теорией струн породил большинство новых глубоких идей в области физики частиц, эволюции Вселенной, тяготения и теории струн. Теоретик-струнник со своим знанием грамматики и создатель моделей со своим словарем вдвоем начали писать вполне разумный разговорник.
Сердце вещества
В конечном счете идеи, которые мы будем рассматривать, касаются всей Вселенной. Однако эти идеи уходят корнями в физику частиц и теорию струн, которые призваны описывать мельчайшие компоненты вещества. Поэтому, прежде чем пускаться в путешествие по экстремальным просторам, которые исследуют эти теории, предпримем краткую прогулку вглубь вещества к его мельчайшим составным частям. Во время этой экскурсии по атому обратите внимание на основные строительные блоки вещества и размеры тех объектов, с которыми имеют дело разные физические теории. Они будут служить ориентирами, на которые в дальнейшем можно будет опираться и которые помогут вам осознать составные части, важные для разных областей физики.
Основным исходным пунктом большинства физических теорий является утверждение, что строительными элементами вещества являются элементарные частицы. Счистите все слои, и внутри вы всегда в конце концов обнаружите элементарные частицы. Частичники изучают вселенную, в которой эти объекты считаются мельчайшими элементами. В теории струн делается еще один шаг вперед и постулируется, что сами частицы являются осцилляциями элементарных струн. Однако даже струнники полагают, что вещество состоит из частиц — неразрушимых сущностей в его сердцевине.
Довольно трудно поверить, что все состоит из частиц; безусловно, они не видны невооруженным глазом. Но это есть следствие очень грубой разрешающей способности наших органов чувств, которые не могут непосредственно детектировать какой бы то ни было предмет, близкий по размерам к атому. Тем не менее, даже несмотря на то что мы не можем наблюдать элементарные частицы непосредственно, они являются элементарными строительными блоками вещества. Точно так же как изображения на мониторе вашего компьютера или экране телевизора составлены из крохотных точек, и тем не менее кажутся непрерывными, вещество состоит из атомов, которые, в свою очередь, состоят из элементарных частиц. Физические тела вокруг нас кажутся непрерывными и однородными, но на самом деле это не так.
Прежде, чем физикам удалось заглянуть вглубь вещества и определить его состав, им потребовалось совершить технологический прорыв в создании чувствительных измерительных приборов. Но каждый раз, как они разрабатывали все более точные приборы и технологии, обнаруживалась структура, т. е. более элементарные составные части вещества. И каждый раз, когда физикам удавалось создать приборы, которые могли прощупать еще меньшие размеры, они обнаруживали еще более фундаментальные составные части — субструктуру, т. е. составные части известных ранее структурных элементов.
Цель физики частиц состоит в открытии самых основных составных частей вещества и самых фундаментальных физических законов, которым подчиняются эти составные части. Мы изучаем малые масштабы расстояний, потому что элементарные частицы взаимодействуют на этих расстояниях и фундаментальные силы легче разделить. На больших расстояниях базовые составные части связаны в сложные объекты, так что фундаментальные физические законы распутываются с трудом и становятся поэтому более смутными. Малые масштабы расстояний интересны потому, что там действуют новые принципы и связи.
Вещество — не просто матрешка, внутри которой находятся все меньшие и меньшие копии похожих куколок. На малых расстояниях обнаруживаются поистине новые явления. Даже функционирование человеческого организма — например, работу сердца и механизм кровообращения — люди плохо представляли себе до тех пор, пока ученые, такие как Уильям Гарвей, не произвели в 1600-х годах вскрытие человеческого тела и не заглянули внутрь. Недавние эксперименты проделали то же самое с веществом, исследуя малые расстояния, на которых новые миры взаимодействуют за счет более фундаментальных физических законов. И точно так же, как циркуляция крови имеет важное значение для функционирования всего организма, фундаментальные физические законы приводят к важным следствиям для нас на больших масштабах.
Мы знаем теперь, что все вещество состоит из атомов, которые за счет химических процессов объединяются в молекулы. Атомы очень малы, их размер порядка ангстрема или одной сотой части от миллионной доли сантиметра. Но атомы не фундаментальны, они состоят из положительно заряженного ядра, окруженного отрицательно заряженными электронами (рис. 30). Ядро много меньше, чем атом, и занимает по размеру лишь одну стотысячную долю атома. Но положительно заряженное ядро само является составным. Оно содержит положительно заряженные протоны и нейтральные (незаряженные) нейтроны, которые вместе называют нуклонами и которые ненамного меньше самого ядра. Такова была картина устройства вещества, которая была принята учеными до 1960-х годов и которую вы, вполне возможно, изучали в школе.
Эта схема атома правильна, хотя, как мы увидим ниже, квантовая механика приводит к более интересной картине орбит электронов, чем любая картинка,

которую вы можете нарисовать. Но мы теперь знаем, что протоны и нейтроны не являются фундаментальными частицами. В противоположность приведенному во введении высказыванию Гамова, у протона и нейтрона есть субструктура, более фундаментальные составные части, известные как кварки. Протон состоит из двух u-кварков и одного d-кварка, а нейтрон содержит два d-кварка и один и-кварк (рис. 31) [30]. Эти кварки связаны друг с другом ядерными силами, известными как сильное взаимодействие. Электрон, другой компонент атома, ведет себя иначе. Насколько мы можем судить, он фундаментален — электрон невозможно разделить на более мелкие частицы, он не содержит внутри себя никакой субструктуры.
Нобелевский лауреат, физик Стивен Вайнберг придумал название «Стандартная модель» для обозначения хорошо установленной теории в физике частиц, которая описывает взаимодействия этих фундаментальных строительных блоков вещества — электронов, и- и d-кварков, а также других фундаментальных частиц, к которым мы сейчас перейдем. Стандартная модель описывает также три из четырех сил, за счет которых взаимодействуют элементарные частицы: электромагнетизм, слабое взаимодействие, сильное взаимодействие (гравитация обычно опускается).

Хотя гравитация и электромагнетизм были известны в течение столетий, вплоть до второй половины двадцатого века никто не понимал две последние, менее знакомые силы. Эти слабые и сильные взаимодействия влияют на фундаментальные частицы и очень важны для ядерных процессов. Они, например, позволяют кваркам связываться вместе, а нуклонам распадаться.
Если угодно, мы можем также включить гравитацию в Стандартную модель. Обычно это не делается, так как гравитация — слишком слабая сила, чтобы иметь какое либо значение на расстояниях, имеющих отношение к физике частиц при экспериментально доступных энергиях. При очень больших энергиях и на очень малых расстояниях наши обычные представления о гравитации терпят крах. Это важно для теории струн, но не играет роли на измеримых масштабах расстояний. При изучении элементарных частиц гравитация важна только для определенных расширений Стандартной модели, таких как модели с дополнительными измерениями, которые мы позднее рассмотрим. Для всех остальных предсказаний о поведении элементарных частиц про гравитацию можно забыть.
Теперь, когда мы вошли в мир фундаментальных частиц, нам стоит немного оглядеться и произвести переучет наших соседей. Кварки и и d, а также электрон образуют сердцевину вещества. Однако сегодня мы знаем, что существуют также дополнительные, более тяжелые кварки и другие электроноподобные частицы, которые никогда не обнаруживаются в обычном веществе. Например, в то время как электрон имеет массу порядка одной двухтысячной доли массы протона, частица, называемая мюоном, имеет такой же заряд, как у электрона, и массу, в двести раз больше, чем у электрона. Частица по имени тау, также имеющая тот же заряд, имеет массу еще в десять раз большую. За последние тридцать лет в экспериментах на коллайдерах высокой энергии были обнаружены еще более тяжелые частицы. Чтобы породить их, физикам потребовалось самое большое количество сконцентрированной энергии, какое только могут создать современные ускорители частиц.
Я сознаю, что этот раздел был объявлен как экскурсия внутрь вещества, но частицы, о которых я говорю, не содержатся внутри стабильных объектов материального мира. Хотя все известное вещество состоит из элементарных частиц, более тяжелые элементарные частицы не являются составными частями вещества. Вы не обнаружите их в шнурках своих туфель, на поверхности своего стола, на Марсе, или в любом другом известном нам физическом объекте. Однако эти частицы постоянно создаются в наши дни в экспериментах на коллайдерах высоких энергий, и они были частью ранней Вселенной сразу же после Большого взрыва.
Тем не менее эти тяжелые частицы являются существенными компонентами Стандартной модели. Они взаимодействуют за счет тех же сил, что и более знакомые частицы, и возможно, будут играть важную роль в более глубоком понимании наиболее фундаментальных законов природы, которым подчиняется вещество. На рис. 32 и 33 я перечислила частицы Стандартной модели. Я включила в список нейтрино и переносчиков сил — калибровочные бозоны, — о которых мы поговорим подробнее в гл. 7, где я детальнее рассмотрю все элементы Стандартной модели.

Никто не знает, почему существуют тяжелые частицы Стандартной модели. Вопросы о цели их существования, той роли, которую они играют в окончательной теории, о том, почему их массы столь отличны от масс составных частей более знакомого вещества, являются некоторыми из важнейших загадок, с которыми сталкивается Стандартная модель. И это лишь часть того, на что не может ответить Стандартная модель. Почему, например, имеются четыре силы, а не больше? Могут ли существовать другие силы, которые мы до сих пор не обнаружили? И почему гравитация настолько слабее других известных сил?
В Стандартной модели остается открытым и более теоретический вопрос, который надеется разрешить теория струн: каким образом мы должны самосогласованно объединить квантовую механику и гравитацию на всех масштабах расстояний? Этот вопрос отличается от других тем, что он касается не наблюдаемых в данное время явлений, а внутренних ограничений физики частиц.
Оба типа остающихся без ответа вопросов, которые касаются как наблюдаемых явлений, так и чисто теоретических проблем, дают нам основания выйти за рамки Стандартной модели. Несмотря на мощь и успехи Стандартной модели, мы уверены, что более фундаментальная структура ожидает своего открытия, а поиск более фундаментальных принципов будет вознагражден. Как изящно заметил на страницах «Нью-Йорк Таймс» композитор Стив Райх (проводя аналогию с той пьесой, которую он сочинял): «Сначала были просто атомы, затем появились протоны и нейтроны, после них — кварки, а теперь мы говорим о теории струн. Похоже, что каждые 20, 30, 40, 50 лет открывается люк, и перед нами предстает следующий уровень реальности».
В экспериментах на работающих и строящихся коллайдерах уже не ищут ингредиенты Стандартной модели, они уже все найдены. Стандартная модель изящно организует эти частицы по их взаимодействиям, так что сейчас известен полный набор частиц этой модели. Вместо этого экспериментаторы ищут частицы, которые могут оказаться еще интереснее. Современные теоретические модели включают составные части Стандартной модели, но добавляют новые элементы для решения ряда вопросов, оставшихся в Стандартной модели нерешенными. Мы надеемся, что текущие и будущие эксперименты дадут нам ключи, которые позволят разобраться с этими вопросами и открыть истинную, основополагающую природу вещества.
Хотя у нас есть кое-какие экспериментальные и теоретические догадки о природе более фундаментальной теории, мы вряд ли узнаем, каково правильное описание природы, пока ответ не дадут эксперименты при высоких энергиях (которые исследуют малые расстояния). Как мы увидим позже, теоретические соображения говорят, что эксперименты в следующем десятилетии почти наверняка откроют что-то новое. Возможно, это не будет явное свидетельство в пользу теории струн, которое очень трудно добыть, но, может быть, мы увидим что-то экзотичное, вроде новых взаимосвязей в пространстве-времени, или новых, но до сих пор невидимых дополнительных измерений — новые явления, характерные для теории струн, а также других теорий в физике частиц. И несмотря на широкий диапазон нашего коллективного воображения, эти эксперименты также могут обнаружить нечто, о чем никто из нас и не думал. Мои коллеги и я с любопытством ожидают, что бы это могло быть.
Анонс
Мы знаем, что та структура вещества, которую мы только что обсудили, есть результат важнейших физических открытий прошлого века. Эти грандиозные успехи существенны для любой более всеобъемлющей теории мира, которую мы хотели бы построить, и сами по себе ознаменовали крупные достижения.
Начиная со следующей главы, мы сделаем обзор этих открытий. Теории вырастают из наблюдений и недостатков предшествующих теорий, так что вы сможете лучше понять роль современных достижений, если познакомитесь с выдающимися успехами более ранних эпох. На рис. 34 показаны связи между теориями, которые мы будем обсуждать. Мы увидим, как новые теории вырастали на уроках старых теорий, и как новые теории заполнили пробелы, обнаруженные только после того, как были завершены старые теории.

Мы начнем с двух революционных идей первых лет двадцатого века — теории относительности и квантовой механики, с помощью которых была установлена форма Вселенной и содержащихся в ней тел, а также состав и структура атома. Затем мы рассмотрим Стандартную модель физики частиц, развитую в 1960-1970-е годы для предсказания взаимодействий элементарных частиц, с которыми мы только что познакомились. Наконец, мы познакомимся с наиболее важными принципами и понятиями физики частиц: симметрией, нарушением симметрии и зависимостью физических величин от масштаба, с помощью которых мы узнаем многое о том, как самые элементарные компоненты вещества образуют наблюдаемую нами структуру.
Однако, несмотря на большие успехи, Стандартная модель физики частиц оставляет без ответа многие фундаментальные вопросы, которые настолько важны, что их решение позволит проникнуть в структуру строительных элементов нашего мира. В гл. 10 будет рассмотрен один из самых интересных и загадочных механизмов Стандартной модели: происхождение масс элементарных частиц. Мы увидим, что для объяснения массы известных частиц и слабости гравитации почти наверняка потребуется более глубокая физическая теория, чем Стандартная модель.
Подобные проблемы физики частиц исследуются в моделях с дополнительными измерениями, но при этом также используются идеи теории струн. Обсудив основы физики частиц, мы перейдем к фундаментальные понятиям и принципам теории струн. Мы не хотим выводить модели непосредственно из теории струн, но эта теория содержит ряд элементов, которые используются при разработке моделей с дополнительными измерениями.
Этот обзор охватывает много теоретических положений, так как анализ дополнительных измерений связывает между собой многие теоретические достижения на двух главных берегах физики частиц — создании моделей и теории струн. Знакомство с многими наиболее интересными современными достижениями в этих областях поможет вам лучше понять мотивацию и методы, лежащие в основе развития моделей с дополнительными измерениями.
Однако, если вы хотите быстрее продвинуться вперед, я заканчиваю каждую из обзорных глав маркированным списком важнейших понятий, на которые мы будем ссылаться далее, когда вернемся к созданию моделей с дополнительными измерениями. Маркеры будут служить коротким путем, резюме, если вы захотите пропустить главу или захотите сфокусировать внимание на материале, к которому мы обратимся далее. Иногда я буду ссылаться и на вопросы, не отмеченные маркером, но эти маркеры будут давать обзор ключевых идей, существенных для главных результатов в оставшейся части книги.
В гл. 17 мы приступаем к исследованию миров с дополнительными измерениями — теориям, в которых предполагается, что материя, из которой состоит наша Вселенная, сосредоточена на бране. Идеи мира на бране позволяют глубже проникнуть в общую теорию относительности, физику частиц и теорию струн. В разных мирах на бране, которые я опишу, делаются разные предположения и объясняются разные явления. Я суммирую конкретные свойства каждой модели и отмечаю их маркером в конце этих глав. Мы до сих пор не знаем, какая из этих идей правильно описывает природу. Однако вполне возможно, что мы в конце концов обнаружим, что браны являются частью космоса, а мы, наряду с другими параллельными вселенными, прикованы к ним.
Одна вещь, которую я поняла, проводя эти исследования, — Вселенная часто обладает большим воображением, чем мы. Иногда свойства Вселенной оказываются настолько неожиданными, что мы только по случайности натыкаемся на них. Открытие таких сюрпризов может быть ошеломляющим. Оказывается, что известные нам физические законы имеют потрясающие следствия.
Приступим теперь к изучению того, что собой представляют эти законы.
II Достижения начала двадцатого века
Глава 5
Относительность: эволюция теории тяготения Эйнштейна
The laws of gravity are very, very strick.
And you’re just bending them for your own benefit.
Billy Bragg[31]
Икар Рашмор III с нетерпением ждал, когда он сможет показать Дитеру свой новый порше. Но как бы он ни гордился новой машиной, еще больше его волновала GPS (Глобальная система позиционирования), которую он недавно самостоятельно разработал и установил.
Икар хотел поразить Дитера, поэтому он убедил своего друга поехать с ним за город. Они сели в машину, Икар запрограммировал конечный пункт маршрута, и друзья отправились в путь. Но, к огорчению Икара, они завершили свое путешествие в неправильном месте — система GPS сработала совсем не так хорошо, как он ожидал. Дитер сразу же предположил, что Икар, должно быть, сделал какую-то нелепую ошибку, например, перепутал метры с футами. Однако Икар не верил, что он мог совершить такую глупость, и поспорил с Дитером, что проблема не в этом.
На следующий день Икар и Дитер устранили некоторые неисправности. Но, к их разочарованию, когда они отправились в путь, GPS работала еще хуже, чем раньше. Икар и Дитер снова принялись искать неполадки, и, наконец, через неделю разочарований на Дитера снизошло озарение, он сделал быстрый расчет и обнаружил поразительную вещь, что без учета общей теории относительности GPS Икара будет накапливать ошибки со скоростью более 10 км в день. Икару казалось, что его порше не настолько быстр, чтобы требовались релятивистские вычисления, но Дитер объяснил ему, что не автомобиль, а сигналы CPS движутся со скоростью светя. Дитер изменил программу так, чтобы учесть изменение гравитационного поля, сквозь которое движутся сигналы GPS. После этого система Икара стала работать не хуже уже имеющихся в продаже коммерческих моделей. Удовлетворенные И кар и Дитер начали планировать новое автомобильное путешествие.
В начале прошлого века английский физик лорд Кельвин сказал: «В физике уже невозможно открыть что либо новое. Все, что осталось, — это все более и более точные измерения».[32] Лорд Кельвин здорово ошибся: очень скоро после того, как он произнес эти слова, в физике началась революция, связанная с теорией относительности и квантовой механикой, и расцвели различные области физики, над которыми люди работают до сих пор. Однако более глубокое утверждение лорда Кельвина о том, что «научное богатство растет согласно закону сложных процентов»[33], безусловно, правильно, и особенно подходит к этим революционным достижениям.
В этой главе рассматривается учение о гравитации и ее развитии от впечатляющего открытия законов Ньютона до революционных достижений теории относительности Эйнштейна. Законы движения Ньютона являются законами классической физики, и в течение столетий они использовались учеными для расчета механического движения, в том числе движения, обусловленного тяготением. Законы Ньютона великолепны, они позволяют нам предсказывать движение с очень большой точностью, достаточной для того, чтобы посылать людей на Луну и выводить спутники на орбиты, для того, чтобы удерживать на рельсах при поворотах сверхскоростные поезда в Европе, для того, чтобы побудить к поиску восьмой планеты, Нептуна, руководствуясь особенностями орбиты Урана. Но, увы, эти законы недостаточны для точной работы GPS.
Невероятно, но используемая сейчас GPS для достижения точности 1 м требует использования общей теории относительности Эйнштейна. Определение изменений глубины снежного покрова на Марсе с помощью лазерного дальномера, установленного на вращающемся по орбите космическом корабле, также требует использования этой теории и позволяет производить измерения с неправдоподобной точностью 10 см. Конечно, когда общая теория относительности была предложена, никто, даже Эйнштейн, не предполагал таких практических приложений столь абстрактной теории.
В этой главе будет рассматриваться теория тяготения Эйнштейна — необычайно точная теория, применимая к широкому кругу систем. Мы начнем с краткого обзора теории тяготения Ньютона, которая хорошо работает при энергиях и скоростях, характерных в повседневной жизни. Затем мы совершим пассаж к тем экстремальным пределам, при которых теория Ньютона терпит неудачу, а именно, к пределу очень большой скорости (близкой к скорости света) и очень большой массы или энергии. В этих предельных случаях ньютоновская теория тяготения заменяется общей теорией относительности Эйнштейна. В рамках этой теории пространство (и пространство-время) эволюционирует от статической стадии к динамической сущности, способной искривляться, двигаться и жить собственной богатой жизнью. Мы рассмотрим эту теорию, те идеи, которые привели к ее созданию, и некоторые экспериментальные тесты, убеждающие физиков в ее справедливости.
Ньютоновское тяготение
Тяготение — это сила, которая удерживает ваши ноги на поверхности и является источником ускорения, возвращающего на Землю брошенный вверх камень. В конце XVI века Галилей показал, что это ускорение одинаково для всех тел на поверхности Земли, независимо от их массы.
Однако это ускорение зависит от того, насколько далеко находится предмет от центра Земли. В более общей формулировке, напряженность поля тяготения зависит от расстояния между двумя массами, т. е. гравитационное притяжение становится слабее, когда тела становятся дальше друг от друга. Кроме того, если гравитационное притяжение создает не Земля, а какое-то другое тело, сила тяготения будет зависеть от массы этого тела.
Исаак Ньютон установил закон всемирного тяготения, который показывает, как гравитационная сила зависит от массы и расстояния. Закон Ньютона утверждает, что сила тяготения между двумя телами пропорциональна массе каждого тела. Тела могут быть любыми: Земля и мяч, Солнце и Юпитер, баскетбольный и футбольный мячи, или любые другие предметы. Чем массивнее тела, тем сильнее притягивающая их сила.
Закон тяготения Ньютона показывает также, как гравитационная сила зависит от расстояния между двумя телами. Как говорилось в гл. 2, закон тяготения утверждает, что сила притяжения между двумя телами обратно пропорциональна квадрату расстояния между ними. Именно в вопросе о законе обратных квадратов вступает в игру знаменитое яблоко[34]. Ньютон мог вывести ускорение яблока вблизи поверхности Земли, создаваемое силой притяжения Земли, и сравнить его с ускорением на поверхности Луны, которая находится в шестьдесят раз дальше от центра Земли, чем поверхность Земли. Ускорение Луны за счет притяжения Земли в 3600 (что равно 602) раз меньше ускорения яблока. Это находится в соответствии с гравитационной силой, уменьшающейся как квадрат расстояния до центра Земли.
Однако, даже когда мы знаем зависимость гравитационной силы притяжения от массы и расстояния, нам все еще требуется дополнительная информация, прежде чем мы сможем определить общую силу гравитационного притяжения. Мы пропустили число, называемое ньютоновской гравитационной постоянной, которое входит в виде множителя при расчете любой классической гравитационной силы. Гравитация очень слаба, и это находит свое отражение в крохотной величине ньютоновской постоянной, которой пропорциональны все гравитационные эффекты.
Гравитационное притяжение Земли или притяжение между Солнцем и планетами может показаться очень большим. Однако это обусловлено только тем, что Земля, Солнце и планеты очень массивны. Ньютоновская постоянная очень мала, так что гравитационное притяжение между элементарными частицами является чрезвычайно малой силой. Эта слабость гравитации является сама по себе большой загадкой, к обсуждению которой мы еще вернемся.
Хотя теория Ньютона была правильной, Ньютон задержал ее публикацию на двадцать лет, до 1687 года, пытаясь все эти годы обосновать ключевое предположение своей теории о том, что гравитационное притяжение Земли было бы таким же, как если бы вся масса Земли была сосредоточена в ее центре. Пока Ньютон был поглощен разработкой дифференциального исчисления, необходимого для решения этой проблемы, Эдмунд Галлей, Кристофер Рен, Роберт Гук и сам Ньютон, анализируя движение планет, орбиты которых измерил Иоганнес Кеплер, установив, что они имеют форму эллипса, добились огромного успеха в определении закона силы тяготения.
Все эти ученые внесли существенные вклады в решение задачи о движении планет, но именно Ньютону мы обязаны формулировкой закона обратных квадратов для тяготения. Дело в том, что именно Ньютон окончательно показал, что эллиптические орбиты возникают как результат действия центральной силы (от Солнца), только если выполняется закон обратных квадратов, и он же показал с помощью дифференциального исчисления, что масса шарообразного тела действует так, как будто она сосредоточена в центре этого тела. Однако Ньютон признавал значение вкладов других ученых, выразив это словами: «Если мне и удалось видеть дальше, то это потому, что я стоял на плечах гигантов» [35]. (Однако, по слухам, он сказал это только потому, что испытывал крайнюю неприязнь к Гуку, который был очень низкого роста.)
В курсе физики в средней школе мы изучали законы Ньютона и рассчитывали поведение интересных (хотя и несколько искусственных) систем. Я вспоминаю свое негодование, когда наш учитель г-н Баумел сообщил, что только что изученная нами теория тяготения неверна. Зачем же преподавать теорию, если известно, что она неверна? С точки зрения моего ученического взгляда на мир, вся ценность науки заключалась в том, что она могла быть правильной и заслуживать доверия, а также могла делать точные и обоснованные предсказания.
Но г-н Баумел слишком упростил проблему, возможно, для эффектности. Теория Ньютона не была неправильной, она всего лишь была неким приближением, которое в большинстве случаев работает исключительно хорошо. Для большой области изменения параметров (скорости, расстояния, массы и пр.) она достаточно точно предсказывает величину силы тяготения. Более точной фундаментальной теорией тяготения является теория относительности, которая приводит к измеримо отличающимся предсказаниям, только если вы имеете дело с чрезвычайно большими скоростями или огромными значениями масс. Закон Ньютона прекрасно предсказывает движение мяча, поскольку не выполнен ни один из указанных выше критериев. Поэтому использовать теорию относительности для предсказания движения мяча было бы чистейшей глупостью.
На самом деле сам Эйнштейн первоначально полагал, что специальная теория относительности является всего лишь уточнением ньютоновской физики, а не радикальным изменением парадигмы. Это, конечно, сильно преуменьшает окончательное значение его работы.
Специальная теория относительности
Весьма разумно ожидать от физических законов, что они должны быть одинаковы для каждого. Никто бы не осудил нас за сомнения в их справедливости и полезности, если бы люди в разных странах, в разных движущихся поездах или летящие в разных самолетах наблюдали бы разные физические законы. Физические законы должны быть фундаментальными и должны выполняться для любого наблюдателя. Любая разница в вычислениях должна объясняться отличиями в окружающей среде, а не в физических законах. Действительно, было бы очень странно иметь универсальные физические законы, требующие конкретной точки наблюдения. От вашей системы отсчета могут зависеть конкретные величины, которые вы можете измерить, но не законы, управляющие этими величинами. Эйнштейновская формулировка специальной теории относительности утверждает, что дело обстоит именно так.
На самом деле несколько удивительно, что работа Эйнштейна по теории тяготения называется «теорией относительности». Принципиальный момент, заложенный как в специальную, так и в общую теорию относительности, состоит в том, что физические законы должны выполняться для всех, независимо от их систем отсчета. В действительности Эйнштейн предпочитал термин Invariantentheorie (теория инвариантности)[36]. В письме, которое написал Эйнштейн в 1921 году в ответ корреспонденту, предлагавшему переделать название, он признал, что термин «относительность» неподходящий[37]. Но к тому времени термин слишком хорошо укоренился, чтобы пытаться его изменить.
Первая идея Эйнштейна о системах отсчета и относительности возникла из размышлений об электромагнетизме. Хорошо известная с середины XIX века теория электромагнетизма была основана на уравнениях Максвелла, описывающих явления электромагнетизма и электромагнитные волны. Эти уравнения приводили к правильным результатам, но с самого начала ученые ошибочно интерпретировали полученные предсказания в рамках движения эфира, гипотетической невидимой субстанции, колебаниями которой и считались электромагнитные волны. Эйнштейн понял, что если эфир существует, то должна существовать и выделенная точка или система отсчета для наблюдений, а именно, та, в которой эфир покоится. Он обосновал, что одни и те же физические законы должны быть применимы к людям, движущимся с постоянной скоростью[38] по отношению к друг другу, а также по отношению к покоящемуся человеку, т. е. в системах отсчета, которые физики называют инерциальными системами. Потребовав, чтобы все физические законы, включая электромагнетизм, выполнялись для наблюдателей во всех инерциальных системах отсчета, Эйнштейн пришел к отказу от идеи эфира и в конце концов создал специальную теорию относительности.
Главным скачком в эйнштейновской специальной теории относительности был радикальный пересмотр понятий пространства и времени. Питер Гейлсон[39], физик и историк науки, полагает, что не только теория эфира натолкнула Эйнштейна на верный путь, но и размышления Эйнштейна над понятием времени.
Гейлсон полагает, что Эйнштейн, выросший в Германии и работавший в патентном бюро в Берне, Швейцария, должен был постоянно думать о времени и его синхронизации. Всякий, кто путешествовал по Европе, знает, что в Германии и Швейцарии очень ценится точность, и замечательным следствием этого является то, что пассажиры всегда могут быть уверены, что поезда следуют строго по расписанию. Эйнштейн работал в патентном бюро с 1902 по 1905 год, в ту эпоху, когда железнодорожное сообщение приобретало все большую важность, а синхронизация времени было передним краем новой технологии. В начале 1900-х годов Эйнштейн очень любил думать о житейских проблемах, например, о том, как синхронизировать время на одной железнодорожной станции со временем на другой.
Конечно, Эйнштейну не требовалось развивать теорию относительности для того, чтобы решить проблему синхронизации движения реальных поездов. (Для тех из нас, кто привык к часто запаздывающим поездам в Америке, синхронизированное время в любом случае может звучать как экзотика[40].) Но синхронизация времени поднимает ряд интересных вопросов. Для релятивистски движущихся поездов синхронизация времени является непростой задачей. Если я хочу синхронизовать мои часы с часами пассажира на движущемся поезде, я должна учесть время запаздывания распространяющегося между нами сигнала, так как свет имеет конечную скорость. Синхронизация моих часов с часами рядом сидящего пассажира — не то же самое, что синхронизация удаленных друг от друга часов[41].
Решающим прозрением Эйнштейна, которое привело его к созданию специальной теории относительности, было понимание необходимости пересмотра представлений о времени. Согласно Эйнштейну, пространство и время не могут более рассматриваться независимо. Хотя они не одно и то же (очевидно, что время и пространство различаются), измеряемые вами величины зависят от скорости вашего движения. Специальная теория относительности стала результатом этого прозрения.
Сколь бы удивительными они ни казались, новые следствия специальной теории относительности Эйнштейна можно вывести из двух постулатов. Чтобы их сформулировать, нам нужно понять, что представляют собой инерциальные системы отсчета. Выберем сначала произвольную систему отсчета, которая движется с постоянной скоростью (имеется в виду, что постоянны и величина скорости и ее направление); часто подходящим примером является покоящаяся система отсчета. Инерциальными системами отсчета будут тогда те системы, которые двигаются с постоянной скоростью по отношению к первой. Например, кто-то бежит или едет с постоянной скоростью.
Постулаты Эйнштейна утверждают, что:
— законы физики одинаковы во всех инерциальных системах отсчета;
— скорость света с одинакова во всех инерциальных системах отсчета.
Эти два постулата говорят нам, что законы Ньютона неполны. Если только мы примем эйнштейновские постулаты, у нас не останется иного выбора, кроме как заменить законы Ньютона новыми физическими законами, совместимыми с этими правилами Следующие отсюда законы специальной теории относительности приводят ко всем тем удивительным следствиям, о которых вы могли уже слышать, таким как замедление времени, зависимость понятия одновременности от наблюдателя и лоренцовское сокращение длины движущегося тела. Если применять новые законы к телам, движущимся со скоростями, малыми по сравнению со скоростью света, эти законы должны сводиться к старым законам классической физики. Но если применять их к каким-то телам, движущимся очень быстро, со скоростью равной или близкой к скорости света, то разница между ньютоновскими законами и законами специальной теории относительности должна стать несомненной.
Например, в ньютоновской механике величины скоростей просто складываются. Автомобиль, мчащийся вам навстречу по шоссе, приближается к вам со скоростью, равной по величине сумме величин вашей и его скоростей. Аналогично, если кто-то, стоящий на платформе, бросает вам мяч, а вы в это время находитесь в приближающемся поезде, величина скорости мяча окажется равной сумме величин скорости самого мяча и скорости движущегося поезда. (Мой бывший студент Витек Скиба может подтвердить это. Он почти потерял сознание, когда в него попал мяч, брошенный кем-то в приближающийся поезд, в котором он ехал.)
Согласно ньютоновской физике, скорость светового луча, направленного на движущийся поезд, должна равняться сумме скорости света и скорости движущегося поезда. Но это не может быть верным, если величина скорости света постоянна, как того требует второй постулат Эйнштейна. Если величина скорости света всегда одна и та же, тогда скорость луча, направленного на движущийся поезд, будет такой же, как скорость луча, достигающего вас, когда вы неподвижно стоите на земле. Даже несмотря на то что это противоречит интуиции, дополненной повседневным опытом движения с малыми скоростями, величина скорости света постоянна, а скорости в специальной теории относительности не складываются так же просто, как в ньютоновской физике. На самом деле сложение скоростей происходит согласно релятивистской формуле, вытекающей из постулатов Эйнштейна.
Многие приложения специальной теории относительности не согласуются со знакомыми нам понятиями пространства и времени. Пространство и время в специальной теории относительности рассматриваются иначе, чем в ньютоновской механике, и это приводит ко многим противоречащим интуиции результатам. Измерения времени и пространства зависят от скорости, и сами эти понятия смешиваются в системах, движущихся относительно друг друга. Тем не менее, какими бы странными они ни казались, если вы принимаете два постулата, то изменение понятий пространства и времени есть их неизбежное следствие.
Приведем один аргумент в пользу этого. Представим себе два совершенно одинаковых корабля с одинаковыми мачтами. Один из кораблей стоит на якоре в порту, а другой удаляется от берега. Допустим далее, что капитаны двух кораблей сверили свои часы в момент отплытия одного корабля.
Представим теперь, что два капитана проделывают довольно странную процедуру: каждый из них решает измерить время на своем корабле, поместив одно зеркало на верхушке мачты, а другое — у ее основания, запуская луч света от нижнего зеркала к верхнему и измеряя, сколько раз свет отразится от верхнего зеркала и вернется к нижнему. Конечно, для практических целей такой способ абсурден, так как свет будет периодически двигаться вверх и вниз слишком часто, чтобы можно было успеть сосчитать число отражений. Но доверьтесь мне и представьте, что капитаны могут считать невероятно быстро. Я сейчас использую этот несколько искусственный пример для доказательства того, что на движущемся корабле время растягивается.
Если каждый капитан знает, сколько времени требуется на то, чтобы свет совершил один цикл, он может вычислить пройденный промежуток времени, умножая длительность одного цикла на число циклов, которые свет пробегает между зеркалами. Предположим, однако, что вместо того чтобы использовать свои собственные часы с неподвижными зеркалами, капитан стоящего на якоре корабля измеряет время по числу раз, которые свет на плывущем корабле отражается от зеркала на мачте и возвращается назад.
С точки зрения капитана на плывущем корабле, свет просто движется строго вверх — вниз. Однако, с точки зрения капитана стоящего на якоре корабля, свет должен пройти больший путь (чтобы пройти расстояние, пройденное движущимся кораблем, рис. 35). Однако, и в этом месте наши рассуждения противоречат интуиции, скорость света постоянна. Она одна и та же как для света, посланного к верхушке мачты стоящего на якоре корабля, так и для света, посланного к верхушке мачты движущегося корабля. Так как скорость равна пройденному расстоянию, деленному на время, за которое оно пройдено, а скорость света для движущегося и неподвижного кораблей одинакова, часы, связанные с движущимися зеркалами, должны «тикать» медленнее, чтобы компенсировать большее расстояние, которое должен пройти свет. Этот полностью противоречащий интуиции вывод, что движущиеся и неподвижные часы должны «тикать» с разными скоростями, вытекает из того факта, что скорость света в движущейся системе отсчета совпадает со скоростью света в неподвижной системе. И хотя предложенный способ измерения времени забавен, вывод о том, что движущиеся часы идут медленнее, будет верным независимо от того, как измеряется время. Если у капитанов есть часы, они будут наблюдать то же самое явление (с той оговоркой, что для обычных скоростей эффект будет ничтожно малым).
Хотя приведенный пример несколько искусственный, само описанное явление приводит к непосредственно наблюдаемым явлениям. Например, специальная теория относительности приводит к разным временам жизни быстро движущихся тел. Это явление называется замедлением времени.
Физики измеряют замедление времени, изучая элементарные частицы, рожденные на коллайдерах или в атмосфере, и движущиеся с релятивистскими скоростями, приближающимися к скорости света. Например, элементарная частица, называемая мюон, имеет тот же заряд, что и электрон, но тяжелее его и может распадаться (т. е. превращаться в другие, более легкие частицы). Время жизни мюона, т. е. промежуток времени до его распада, равно всего 2 мкс. Если движущийся мюон имел бы то же время жизни, что и неподвижный, он мог бы пролететь до распада всего около 600 м. Но мюоны ухитряются пролететь через всю нашу атмосферу, а в коллайдерах — до краев больших детекторов, так как благодаря их скорости, близкой к скорости света, нам они кажутся живущими намного дольше. В атмосфере мюоны пролетают расстояние, по крайней мере в десять раз большее, чем они пролетали бы в мире, основанном на ньютоновских принципах. Сам факт, что мы вообще наблюдаем мюоны, показывает, что замедление времени (и специальная теория относительности) приводит к правильным физическим явлениям.
Специальная теория относительности важна не только потому, что она привела к выводам, существенно отклоняющимся от классической физики, но и потому, что она оказалась существенной для развития общей теории относительности и квантовой теории поля, играющих важную роль в новейших исследованиях. Поскольку при дальнейшем обсуждении физики частиц и моделей с дополнительными измерениями я не хочу использовать конкретные предсказания специальной теории относительности, я не поддамся искушению заняться изучением всех поразительных следствий этой теории, например, почему одновременность зависит от того, движется ли наблюдатель или покоится, и как размеры движущихся тел отличаются от размеров покоящихся тел. Вместо этого мы погрузимся в другое интереснейшее исследование, а именно, общую теорию относительности, которая будет важна позднее, когда мы начнем рассматривать теорию струн и дополнительные измерения.
Принцип эквивалентности: начинается общая теория относительности
Специальная теория относительности была опубликована Эйнштейном в 1905 году. В 1907 году, работая над статьей, подводившей итог недавним исследованиям по теории относительности, Эйнштейн задался вопросом, применима ли теория ко всем ситуациям. Он обратил внимание на два главных упущения. С одной стороны, законы физики выглядели одинаково только в некоторых специальных инерциальных системах отсчета, которые двигались с постоянными скоростями относительно друг друга.
В специальной теории относительности эти инерциальные системы занимали привилегированное положение. Теория отбрасывала любую систему отсчета, которая двигалась с ускорением. Когда вы нажимаете педаль газа своего автомобиля, вы уже не находитесь в одной из специальных систем отсчета, в которых применимы законы специальной теории относительности. Отсюда и слово «специальная» в специальной теории относительности: «специальные» инерциальные системы являются лишь малым подмножеством всех возможных систем отсчета. Для человека, убежденного в том, что ни одна система отсчета ничем не лучше другой, тот факт, что теория выделяет инерциальные системы отсчета, представляет большую проблему.
Второе опасение Эйнштейна касалось гравитации. Хотя он представлял себе, как в некоторых ситуациях тела реагируют на тяготение, он еще не мог предложить формул для описания самого гравитационного поля. В некоторых простых случаях вид закона для силы тяготения был известен, однако Эйнштейн все еще не мог вывести выражение для поля в случае произвольного распределения материи.
В период между 1905 и 1915 годами, иногда доходя до полного изнеможения, Эйнштейн исследовал эти проблемы. Результатом явилась общая теория относительности. В основу новой теории он поместил принцип эквивалентности, утверждавший, что эффекты, вызванные ускорением, невозможно отличить от эффектов гравитации. Все законы физики должны выглядеть одинаково как для ускоренного наблюдателя, так и для неподвижного наблюдателя, помещенного в гравитационное поле, ускоряющее все тела в неподвижной системе отсчета с ускорением той же величины, но противоположного направления по сравнению с ускорением исходного наблюдателя. Иными словами, у вас нет способа отличить постоянное ускорение от состояния покоя в гравитационном поле. Согласно принципу эквивалентности, не существует измерения, которое могло бы отличить эти две ситуации. Наблюдатель никогда не узнает, в какой ситуации он находится. Принцип эквивалентности вытекает из эквивалентности инертной и гравитационной масс, двух величин, которые в принципе могли бы отличаться друг от друга. Инертная масса определяет, каким образом тело реагирует на любую силу, т. е. какое ускорение приобретет тело в результате приложения данной силы. Роль инертной массы следует из второго закона движения Ньютона F = mа, утверждающего, что если вы приложите силу величиной F к телу массой m, то оно приобретет ускорение а. Знаменитый второй закон Ньютона утверждает, что данная сила сообщает меньшее ускорение телу с большей инертной массой, что, вероятно, знакомо вам из повседневной жизни. (Если вы толкнете скамеечку для ног, она отлетит дальше и быстрее, чем если бы вы толкнули с той же силой большой рояль.) Обратим внимание на то, что этот закон применим для сил любого рода, например, для электромагнетизма. Он может применяться в ситуациях, не имеющих никакого отношения к гравитации.
С другой стороны, гравитационная масса есть та масса, которая входит в закон для силы тяготения и определяет интенсивность гравитационного притяжения. Как мы видели, интенсивность ньютоновской силы тяготения пропорциональна двум массам, которые притягиваются друг к другу. Эти массы и есть гравитационные массы. Оказывается, что гравитационные массы и инертные массы, входящие во второй закон Ньютона, равны друг другу, поэтому мы можем, не рискуя ошибиться, назвать их одинаковым словом масса. Но в принципе они могли бы быть разными, и одну нужно было бы называть «масса», а другую — «ассам». К счастью, этого делать не нужно.
Загадочный факт равенства этих двух масс имеет глубокие следствия, для установления и развития которых понадобился такой ум, как у Эйнштейна. Закон гравитационной силы утверждает, что сила тяготения пропорциональна массе, а закон Ньютона говорит нам, какое ускорение будет создано этой (или любой другой) силой. Так как сила тяготения пропорциональна той же массе, которая определяет величину ускорения, то два закона совместно утверждают, что несмотря на то, что сила зависит от массы в силу закона F = та, ускорение, вызванное тяготением, не зависит от ускоряемой массы.
Ускорение силы тяжести, которое испытывает любое тело, должно быть одинаковым для всего или всех, находящихся на одном и том же расстоянии от другого тела. Именно это утверждение якобы проверял Галилей, бросая тела с Пизанской башни[42] и демонстрируя, что Земля придает одинаковое ускорение всем телам независимо от их массы. Тот факт, что ускорение не зависит от массы ускоряемого тела, есть уникальное свойство силы тяготения, так как ни одна другая сила не обладает зависящей от массы интенсивностью. Поскольку масса одинаковым образом входит в закон для силы тяготения и ньютоновский закон движения, при расчете ускорения она сокращается. Таким образом, ускорение не зависит от массы.
Этот сравнительно простой вывод приводит к глубоким следствиям. Все тела имеют одинаковое ускорение в однородном гравитационном поле, поэтому если это единственное ускорение можно нейтрализовать, то исчезнут и все свидетельства наличия тяготения. Именно это происходит со свободно падающим телом: оно ускоряется точно так, чтобы уничтожить свидетельства о наличии тяготения.
Принцип эквивалентности утверждает, что если вы и все вокруг вас находятся в состоянии свободного падения, вы не будете сознавать наличие гравитационного поля. Ваше ускорение будет компенсировать то ускорение, которое в противном случае порождалось бы гравитационным полем. Подобное состояние невесомости знакомо по телевизионным передачам с борта спутников, где видно, что космонавты и окружающие их тела не испытывают тяготения.
В учебниках отсутствие эффектов тяготения (с выделенной точки зрения свободно падающего наблюдателя) часто иллюстрируется картинкой человека, выпускающего из рук мяч в свободно падающем лифте. На картинке вы видите, что человек и мяч падают вместе. Человек в лифте будет все время видеть мяч на одной и той же высоте над полом лифта. Он не будет видеть падения мяча (рис. 36).
В учебниках по физике свободно падающий лифт всегда представляется как самая естественная в мире вещь, в которой наблюдатель внутри может хладнокровно, с полной невозмутимостью наблюдать отсутствие падения мяча, совершенно не беспокоясь о своей собственной судьбе. Это находится в резком противоречии с охваченными ужасом лицами людей в кинокартинах, где обрываются тросы лифта и актеры с грохотом рушатся на пол. Почему же возникают столь разные реакции? Если все вокруг находится в состоянии свободного падения, то нет причин для тревоги. Ситуация будет неотличима от покоящегося тела, хотя и в отсутствии гравитационного поля. Однако, если кто-то, как в кино, падает, но пол под ним остается неподвижным, ему самое время остолбенеть от ужаса. Если кто-то находится в свободно падающем лифте, но его тихо поджидает твердый пол, можете быть уверены, что человек заметит последствия тяготения, когда его свободное падение закончится (см. рис. 36).
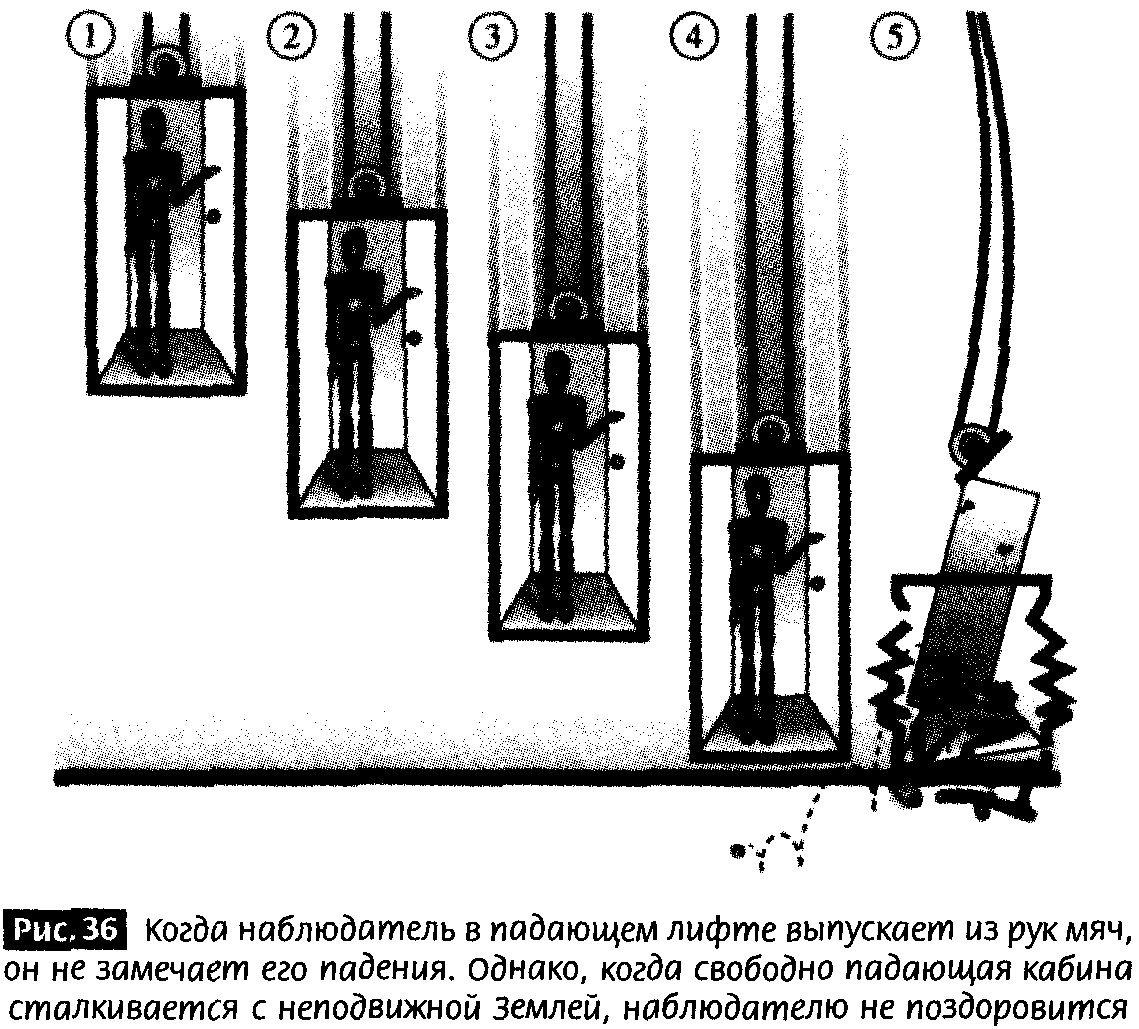
Заключение Эйнштейна кажется столь удивительным и странным, потому что наше воспитание здесь, на Земле, с неподвижной планетой под ногами, сбивает с толку нашу интуицию. Когда сила тяжести на Земле удерживает вас неподвижно на ее поверхности, вы наблюдаете эффекты тяготения, так как не падаете к центру Земли, куда влечет вас тяготение. На Земле мы привыкли к тому, что тяготение заставляет тела падать. Но «падение» на самом деле означает «падение относительно нас». Если бы мы падали вниз вместе с брошенным мячом, как это происходит в свободно падающем лифте, мяч не падал бы быстрее нас. Поэтому мы не видели бы этого падения.
В вашей свободно падающей системе отсчета все законы физики будут совпадать с законами физики, выполняющимися, если вы и все вокруг вас находится в состоянии покоя. Свободно падающий наблюдатель будет видеть, что движение описывается теми же уравнениями, согласующимися со специальной теорией относительности, которые применимы для наблюдателя в инерциальной неускоренной системе отсчета. В обзорной статье 1907 года, посвященной теории относительности, Эйнштейн объясняет, почему гравитационное поле имеет только относительное существование, «так как для свободно падающего с крыши дома наблюдателя, по крайней мере, в непосредственном окружении, отсутствует гравитационное поле»[43].
Это было самое глубокое прозрение Эйнштейна. Уравнения движения для свободно падающего наблюдателя являются уравнениями движения для наблюдателя в инерциальной системе отсчета. Свободно падающий наблюдатель не ощущает силы тяготения; влияние силы тяготения испытывают только тела, которые не находятся в свободном падении.
В нашей жизни мы в общем-то редко наблюдаем вещи или людей, находящихся в свободном падении. Если такое падение происходит, оно вызывает ужас. Но, как сказал один ирландец физику Рафаэлю Буссо, когда он осматривал Скалы Мохера в Ирландии: «Вас убивает не падение, а чертов удар при остановке». Когда я поломала несколько костей во время несчастного случая при восхождении и вынуждена была пропустить конференцию, которую сама же организовала, там ходило несколько шуток о том, как я проверяла теорию тяготения. Могу утверждать с полной уверенностью, что значение ускорения силы тяжести совпадает с предсказаниями.
Проверка общей теории относительности
Можно много говорить об общей теории относительности; скоро мы перейдем к рассмотрению остальных разделов, развитие которых потребовало значительно больше времени. Но уже один принцип эквивалентности объясняет многие результаты общей теории относительности. В тот момент, когда Эйнштейн заметил, что тяготение может быть устранено в ускоренной системе отсчета, он получил возможность вычислять влияние гравитации, представив ускоренную систему, эквивалентную системе с гравитацией. Это позволило ему вычислить гравитационные эффекты для ряда интересных систем, так что другие ученые смогли использовать их для проверки его выводов. Рассмотрим несколько наиболее важных экспериментальных тестов.
Во-первых, это гравитационное красное смещение света. В результате красного смещения мы принимаем световые волны меньшей частоты, чем та, с которой они были испущенны. (Вы, вероятно, встречались с аналогичным эффектом для звуковых волн, когда мотоцикл с ревом мчится мимо вас, и высота звука мотора нарастает, а затем падает.)
Есть несколько способов объяснить происхождение гравитационного красного смещения, но, вероятно, простейший — это объяснение по аналогии. Представьте, что вы подбросили вверх мяч. Поднимающийся мяч постепенно замедляется, двигаясь противоположно направлению силе тяжести. Но энергия мяча не потеряна, даже если он замедляется. Эта энергия превращается в потенциальную энергию, которая затем, когда мяч падает вниз, превращается в кинетическую энергию, или энергию движения.
Такое же объяснение применимо к частице света фотону. Точно так же, как мяч теряет импульс, если его подбросить вверх в воздухе, фотон теряет импульс, когда он пытается избавиться от влияния гравитационного поля. Как и в случае мяча, это означает, что фотон теряет кинетическую энергию, но приобретает потенциальную энергию, пробивая себе путь из гравитационного поля. Но фотон не может замедлиться, как это происходит с мячом, так как фотон всегда летит с постоянной скоростью света. Забегая вперед, мы увидим в следующей главе, что одно из следствий квантовой механики гласит: фотон уменьшает свою энергию, когда он уменьшает свою частоту. Именно это и происходит с фотоном, пролетающим сквозь область с переменным гравитационным потенциалом. Чтобы уменьшить свою энергию, фотон уменьшает свою частоту, и эта уменьшившаяся частота и представляет собой гравитационное красное смещение.
Наоборот, фотон, движущийся к источнику гравитационного поля, будет увеличивать свою частоту. В 1965 году физик канадского происхождения Роберт Паунд и один из его студентов Глен Ребка измерили этот эффект, изучив гамма-излучение, испущенное образцом радиоактивного железа, помещенным на верхушке «башни» в гарвардской лаборатории им. Джефферсона, — том здании, где я сейчас работаю. (Хотя приподнятый фронтон лаборатории им. Джефферсона и этажи под ним являются частью всего здания, их называют «башней».) Гравитационные поля на вершине и у основания башни несколько различаются, так как вершина находится чуть дальше от центра Земли. Высокая башня лучше всего подходит для такого эксперимента, так как при этом увеличивается разность высот между местом, откуда испускается гамма-излучение (вершина башни), и местом, где оно регистрируется (основание башни). Но даже несмотря на то, что вся башня состоит из трех этажей, фронтона и нескольких окон над ним, и вся ее высота равна около 22 м, Паунду и Ребке удалось с немыслимой точностью, равной пяти миллионным от миллиардной доли, измерить разность частот между испущенными и поглощенными фотонами. Таким образом, они установили, что предсказания общей теории относительности для гравитационного красного смещения были верны с точностью, равной по меньшей мере 1 %.
Второе экспериментально наблюдаемое следствие принципа эквивалентности — это отклонение луча света. Гравитация может притягивать не только массу, но и энергию. В конце концов, знаменитое соотношение E = mc2 означает, что энергия и масса тесно связаны. Если масса испытывает тяготение, это же должно быть верно и для энергии. Тяготение Солнца влияет не только на массу, но и на траекторию луча света. Теория Эйнштейна точно предсказывает величину отклонения луча света под влиянием Солнца. Эти предсказания были впервые подтверждены во время солнечного затмения 1919 года.
Английский ученый Артур Эддингтон организовал экспедиции на остров Принсипе у берегов Западной Африки и в город Собрал в Бразилии, где можно было наилучшим образом наблюдать затмение. Цель ученых состояла в том, чтобы сфотографировать звезды в окрестности закрытого Луной Солнца и проверить, не сдвинулись ли изображения соседних к Солнцу звезд по отношению к своим обычным положениям. Если окажется, что звезды сдвинулись, это будет означать, что свет от них двигался по искривленной траектории. (Ученые должны производить измерения во время солнечного затмения, для того чтобы солнечный свет не подавлял намного более слабый свет звезд.) Было установлено, что звезды оказались на предсказанных «неправильных» местах. Измерение соответствующего угла отклонения дало сильное подтверждение в пользу общей теории относительности Эйнштейна.
Невероятно, но отклонение луча света сейчас настолько хорошо установлено и объяснено, что оно стало одним из инструментов, используемых для исследования распределения масс во Вселенной и поиска темной материи в форме маленьких выгоревших звезд, уже не испускающих свет. Такие объекты очень трудно увидеть, так же как черных кошек в безлунную ночь. Единственный способ наблюдать эти объекты — это воспользоваться создаваемыми ими гравитационными эффектами.

Одним из способов, которым астрономы могут изучать темные тела, является гравитационное линзирование. Темные тела, как и все другие, взаимодействуют за счет тяготения. Хотя выгоревшие звезды сами не испускают свет, за ними (с нашей точки зрения) могут находиться яркие тела, свет которых мы видим. Если на пути света от этих звезд нет никакой темной звезды, свет будет распространяться по прямым линиям. Но если свет яркой звезды проходит рядом с темной звездой, он отклонится. Свет, идущий слева от темной звезды, отклонится в противоположном направлении по сравнению со светом, идущим справа, а свет, идущий сверху, отклонится в противоположном направлении, чем свет, идущий снизу. Это создает многократные изображения ярких тел за темной звездой, и явление называется гравитационным линзированием. На рис. 37 показан пример многократного изображения звезды, возникающий в случае, когда находящийся на пути массивный объект отклоняет лучи света в разных направлениях.
Изящные кривые Вселенной
Принцип эквивалентности утверждает, что сила тяготения неотличима от постоянного ускорения. Я рада, что вы добрались до этого места, так как должна покаяться, что переупростила задачу и на самом деле эти две вещи не являются полностью неразличимыми. Почему такое возможно? Если гравитация была бы эквивалентна ускорению, то людям в противоположных полушариях было бы невозможно одновременно падать на Землю. В конце концов, не может же Земля ускоряться одновременно в двух направлениях. Например, гравитационное притяжение в разных направлениях, ощущаемое в Америке и Китае, не может быть объяснено одним ускорением.
Разрешение этого парадокса состоит в том, что принцип эквивалентности утверждает всего лишь возможность локальной замены гравитации ускорением. В разных местах пространства ускорение, заменяющее гравитацию согласно принципу эквивалентности, будет в общем случае иметь разное направление. Ответ на вопрос о китайско-американских отношениях состоит в том, что американская гравитация эквивалентна ускорению в направлении, отличном от направления ускорения, эквивалентного китайской гравитации.
Эта решающая идея привела Эйнштейна к полной переформулировке теории тяготения. Он уже более не рассматривал гравитацию как силу, действующую непосредственно на тело. Вместо этого он описал ее как искажение геометрии пространства-времени, отражающее различные ускорения, необходимые для того, чтобы свести на нет гравитацию в разных местах. Пространство-время является уже не фоном события, а его активным участником. Благодаря общей теории относительности Эйнштейна сила тяготения понимается на языке кривизны пространства-времени, которая, в свою очередь, определяется имеющейся в наличии материей и энергией. Рассмотрим понятие кривизны пространства-времени, на котором основана революционная теория Эйнштейна.
Искривленное пространство и искривленное пространство-время
Математическая теория должна быть внутренне самосогласованной, но, в отличие от научной теории, она не обязана соответствовать внешней физической реальности. Действительно, математики часто черпают вдохновение из того, что они видят в окружающем мире. Такие математические объекты, как кубы или натуральные числа, имеют свои аналоги в реальном мире. Однако математики расширяют предположения об этих знакомых понятиях на объекты, чья физическая реальность менее очевидна, например, на тессеракты (гиперкубы в четырехмерном пространстве) и кватернионы (экзотическая система чисел).
В третьем веке до н. э. Евклид сформулировал пять основных постулатов геометрии. Из этих предположений развилась красивая логическая структура, с которой вы, возможно, соприкоснулись в старших классах школы. Однако позднее математики стали проявлять беспокойство в отношении пятого постулата, известного как постулат о параллельных. Этот постулат утверждает, что если заданы прямая и точка вне этой прямой, то существует одна и только одна прямая, которую можно провести через заданную точку параллельно заданной прямой.
В течение двух тысячелетий после того, как Евклид сформулировал свои постулаты, математики спорили о том, является ли пятый постулат действительно независимым, или он может быть логическим следствием остальных четырех. Может ли существовать система геометрии, в которой были бы верны все постулаты, кроме последнего? Если такой системы геометрии не существует, пятый постулат не может быть независимым, и должен поэтому выводиться.
Только в девятнадцатом веке математики поставили пятый постулат на должное место. Великий немецкий математик Карл Фридрих Гаусс обнаружил, что пятый постулат Евклида был тем самым, что утверждал Евклид, — постулатом, который мог быть заменен другим. Гаусс продвинулся вперед и сделал эту замену, открыв другие системы геометрии и демонстрируя таким образом, что пятый постулат независим. Так родилась неевклидова геометрия.
Русский математик Николай Иванович Лобачевский также развивал неевклидову геометрию, но когда он послал свою работу Гауссу, ему пришлось испытать разочарование, узнав, что старый математик за пятьдесят лет до этого пришел к тем же идеям. Однако ни Лобачевский, ни кто-либо другой не знали о результатах Гаусса, которые немецкий ученый скрыл из опасения, что коллеги подвергнут его осмеянию.
Гауссу не следовало беспокоиться. Очевидно, что пятый постулат не всегда верен, так как все мы знаем альтернативные возможности. Например, линии долготы встречаются на Северном полюсе и на Южном полюсе, даже несмотря на то, что они параллельны на экваторе. Примером неевклидовой геометрии является геометрия на сфере. Если бы древние народы писали на сферах, а не на табличках, этот пример был бы для них совершенно очевиден.
Однако существует много примеров неевклидовых геометрий, которые в противоположность сфере не могут быть физически реализованы в трехмерном мире. Первые неевклидовы геометрии Гаусса, Лобачевского и венгерского математика Яноша Больяи[44] имели дело с такими не имеющими наглядного образа теориями, поэтому неудивительно, что для их открытия понадобилось столько времени.
Несколько примеров показывают, что делает искривленные геометрии отличными от плоской геометрии данной страницы. На рис. 38 показаны три двумерные поверхности. Первая, поверхность сферы, обладает постоянной положительной кривизной. Вторая, кусок плоскости, имеет нулевую кривизну. Третья, гиперболический параболоид, обладает постоянной отрицательной кривизной. Примерами поверхностей с отрицательной кривизной являются лошадиное седло, местность между двумя горными вершинами и картофельные чипсы «Прингле».
Существует много безошибочных показателей, с помощью которых можно узнать, каким из трех возможных типов кривизны обладает данное геометрическое пространство. Например, на каждой из трех поверхностей можно нарисовать треугольник. На плоской поверхности сумма углов треугольника всегда равна ровно 180°. Но что можно сказать о треугольнике на поверхности сферы, одна вершина которого находится на Северном полюсе, а две остальные — на экваторе, на четверти расстояния вдоль экватора друг от друга? Каждый из углов этого треугольника равен прямому углу 90°. Поэтому сумма углов треугольника равна 270°. Такого никогда не может быть на плоской поверхности, но на поверхности с положительной кривизной сумма углов треугольника может превышать 180°, так как сама поверхность выпятилась наружу.

Аналогично, сумма углов треугольника, нарисованного на гиперболическом параболоиде, всегда меньше 180°, что отражает отрицательность кривизны этой поверхности. Увидеть это несколько сложнее. Нарисуйте две вершины вблизи вершины седла и одну внизу, в той части гиперболического параболоида, где должна находиться ваша нога, когда вы сидите на лошади. Такой угол меньше того, который получился бы, если бы поверхность была плоской. Сумма углов оказывается меньше 180°.
Как только было установлено, что неевклидовы геометрии внутренне непротиворечивы, т. е. не приводят к парадоксам и противоречиям, немецкий математик Георг Фридрих Бернхард Риман развил богатую математическую теорию для их описания. Кусок бумаги нельзя свернуть в сферу, но можно свернуть в цилиндр. Вы не можете разгладить седло без разрывов или налезания частей друг на друга. Основываясь на работе Гаусса, Риман создал математический формализм, включающий подобные факты. В 1854 году он нашел общее решение задачи о характеристиках всех геометрий с помощью их внутренних свойств. Работы Римана заложили основу современной области математики — дифференциальной геометрии, ветви математики, изучающей поверхности и геометрию.
Так как с этого момента я буду почти всегда рассматривать пространство и время совместно, мы увидим, что, вообще говоря, понятие пространства-времени более полезно, чем понятие пространства. Пространство-время имеет на одно измерение больше, чем пространство: в дополнение к «вверх — вниз», «налево-направо» и «вперед — назад» имеется еще время. В 1908 году математик Герман Минковский использовал геометрические понятия для развития этой идеи об абсолютной пространственно-временной структуре. В то время как Эйнштейн изучал пространство-время, используя временную и пространственные координаты, зависевшие от системы отсчета, Минковский определил независящую от наблюдателя пространственно-временную структуру, которую можно использовать для характеристики данной физической ситуации.
В оставшейся части книги, когда я буду говорить о размерности, я буду указывать число пространственно-временных измерений, если явно не указано иное. Например, когда мы глядим вокруг себя, мы видим то, что с этого момента я буду называть четырехмерной Вселенной. Иногда я буду выделять время и говорить о «3+ 1»-мерной Вселенной или о трех пространственных измерениях. Имейте в виду, что все эти термины относятся к одной и той же системе, имеющей три пространственных и одно временное измерения.
Структура пространства-времени — очень важное понятие. Оно сжато характеризует геометрию, соответствующую гравитационному полю, порожденному заданным распределением энергии и вещества. Но Эйнштейн с самого начала отвергал эту идею, которая казалась ему похожей на излишний надуманный способ переформулировать физику, которую он только что объяснил. Однако в конце концов он заметил, что пространственно-временная структура оказалась существенной для полного описания общей теории относительности и расчета гравитационных эффектов. (Для протокола, Минковский тоже не был слишком поражен Эйнштейном при первом знакомстве. На основании поведения Эйнштейна, когда тот был студентом в классе Минковского по дифференциальному исчислению, Минковский заключил, что Эйнштейн был «лентяем».)
Эйнштейн не был одинок в своем отрицании неевклидовой геометрии. Его друг, шведский математик Марсель Гроссман также считал ее чрезмерно сложной и пытался отговорить Эйнштейна от ее использования. Однако они в конце концов согласились, что единственный поддающийся анализу способ объяснения гравитации должен заключаться в использовании неевклидовой геометрии для описания пространственно-временной структуры. Только после этого Эйнштейн сумел интерпретировать и рассчитать эквивалентное гравитации искривление пространства-времени, что оказалось ключом к завершению общей теории относительности. После того как Гроссман признал поражение, он вместе с Эйнштейном вступил в борьбу с тонкостями дифференциальной геометрии, для того чтобы упростить очень сложные ранние формулировки теории тяготения. В конце концов они завершили общую теорию относительности и достигли более глубокого понимания самой гравитации.
Общая теория относительности Эйнштейна
Общая теория относительности представляет собой радикальный пересмотр понятия гравитации. Сейчас мы понимаем гравитацию — силу, которая удерживает ваши ноги на земле и связывает воедино нашу Галактику со Вселенной, — не как силу, непосредственно действующую на тела, а как следствие геометрии пространства-времени. Эта идея довела взгляды Эйнштейна на единство пространства и времени до своего логического завершения. Общая теория относительности использует глубокую связь между инертной и гравитационной массами, чтобы сформулировать эффекты гравитации только в терминах геометрии пространства-времени. Любое распределение вещества или энергии искривляет или закручивает пространство-время. Изогнутые траектории в пространстве-времени определяют движение под действием гравитации, а наличие вещества и энергии во Вселенной заставляет само пространство-время расширяться, волнообразно изгибаться или сжиматься.
Наикратчайшее расстояние между двумя точками называется геодезической. В плоском пространстве геодезическая представляет собой прямую линию. В искривленном пространстве мы можем определить геодезическую как кратчайший путь между двумя точками, но этот путь уже не обязательно будет прямой линией. Например, маршруты самолетов, летящих по окружностям большого круга на Земле, являются геодезическими. (Окружность большого круга есть любая окружность, представляющая собой границу сечения шара плоскостью, проходящей через его центр, например, линия экватора или линия долготы.) Хотя эти траектории не являются прямыми, они есть кратчайшие пути между двумя точками из тех, которые не проходят сквозь поверхность Земли.
В искривленном четырехмерном пространстве-времени также можно определить геодезические. Для двух событий, разделенных во времени, геодезическая является естественным путем, по которому движутся тела в пространстве-времени, чтобы связать одно событие с другим. Эйнштейн понял, что свободное падение, представляющее путь наименьшего сопротивления, есть движение по пространственно-временной геодезической. Он сделал вывод, что при отсутствии внешних сил брошенные тела будут падать по геодезической, как это происходит с человеком в падающем лифте, не чувствующим своего веса и не видящим, как падает мяч.
Однако, даже когда тела движутся по своим геодезическим сквозь пространство-время и отсутствуют внешние силы, тяготение приводит к заметным эффектам. Мы уже видели, что локальная эквивалентность тяготения и ускорения была одной из решающих идей, заставивших Эйнштейна развить совершенно новый подход к размышлениям о гравитации. Он пришел к выводу, что поскольку вызванное гравитационной силой ускорение локально одинаково для всех масс, гравитация должна быть свойством самого пространства-времени. Это следует из того, что «свободное падение» означает разные вещи в разных местах, и гравитация только локально может быть заменена на простое ускорение. Мой китайский антипод и я падаем в разных направлениях, даже если каждый из нас находится в локальном варианте лифта Эйнштейна. Тот факт, что направление свободного падения неодинаково во всех местах, есть отражение кривизны пространства-времени. Не существует единого ускорения, способного всюду свести к нулю эффекты гравитации. В искривленном пространстве геодезические разных наблюдателей в общем случае различны. Таким образом, глобально гравитация обладает наблюдаемыми следствиями.
Общая теория относительности идет в своих выводах намного дальше ньютоновской гравитации, так как она позволяет нам вычислить релятивистское гравитационное поле любого распределения энергии и вещества. Кроме того, убеждение, что геометрия пространства-времени содержит в себе эффекты тяготения, позволило Эйнштейну закрыть главную брешь в исходной формулировке теории тяготения. Хотя физики того времени знали, как тела должны реагировать на гравитационное поле, они не знали, что такое гравитация. Теперь они поняли, что гравитационное поле есть искажение пространственно-временной структуры, вызванное веществом и энергией. Это искажение распространяется по всему космосу или, как мы вскоре увидим, по многомерному пространству-времени, которое может включать браны. Все гравитационные эффекты, обусловленные такими более сложными ситуациями, могут быть связаны с рябью и искривлением поверхности пространства-времени.
Пожалуй, с помощью картинки лучше всего можно описать, как вещество и энергия искажают структуру пространства-времени, создавая гравитационное поле. На рис. 39 показан находящийся в пространстве массивный шар. Окружающее шар пространство искажено: шар приводит к прогибу пространственной поверхности, глубина которого зависит от массы или энергии шара. Пролетающий вблизи другой шар скатывается к центру прогиба, где сосредоточена масса первого шара. Согласно общей теории относительности, пространственно-временная структура искажается аналогичным образом. Другой пролетающий мимо шар будет ускоряться к центру первого шара. В этом случае результат будет согласовываться с тем, что предсказывает закон Ньютона, но интерпретация движения и его вычисление будут совершенно иными. Согласно общей теории относительности шар следует за неровностями пространственно-временной поверхности и таким образом осуществляет движение, вызванное гравитационным полем.

Рис. 39 может ввести читателя в заблуждение, поэтому следует сделать несколько замечаний. Прежде всего, пространство, окружающее шар, показано двумерным. В действительности, искажены полные трехмерное пространство и четырехмерное пространство-время. Время искажено, потому что с точки зрения специальной и общей теории относительности оно также является измерением. Например, как утверждает специальная теория относительности, искажение времени означает, что часы в разных местах идут с разной скоростью. Следующее замечание состоит в том, что второй мяч, катящийся в искривленной геометрии рядом с первым, будет также влиять на геометрию пространства-времени; мы предположили, что его масса много меньше массы большего шара, и пренебрегли этим малым эффектом. Третье обстоятельство, которое следует иметь в виду, состоит в том, что тело, искажающее пространство-время, может иметь любое количество измерений. Позднее мы увидим, что роль шара в этой картине будет играть брана.
Тем не менее во всех случаях вещество указывает пространству-времени, как изгибаться, а пространство-время указывает веществу, как двигаться. Искривленное пространство-время устанавливает геодезические траектории, вдоль которых в отсутствие других сил перемещаются тела. Гравитация закодирована в геометрии пространства-времени. Эйнштейну потребовалось почти десять лет, чтобы вывести эту точную связь между пространством-временем и тяготением и включить эффекты самого гравитационного поля; помимо всего, гравитационное поле несет энергию и поэтому изгибает пространство-время[45]. На это потребовались героические усилия.
В своих знаменитых уравнениях Эйнштейн показал, как найти гравитационное поле Вселенной, если задано ее содержимое. Хотя самым известным уравнением Эйнштейна является E = mc2[46], физики используют термин «уравнения Эйнштейна» по отношению к уравнениям, определяющим гравитационное поле. Эти уравнения завершают гигантскую задачу, показывая, как определить метрику пространства-времени, зная распределение материи. Вычисляемая метрика определяет геометрию пространства-времени, сообщая нам, как перевести заданные в произвольных единицах числа в физические расстояния и формы, определяющие геометрию.
После окончательной формулировки общей теории относительности физики получили возможность определить гравитационное поле и вычислить его влияние. Как и в предыдущих формулировках гравитации, физики использовали эти уравнения для того, чтобы вычислить, каким образом вещество движется в заданном гравитационном поле. Например, они могут вставить в уравнения массу и положение большого сферического тела вроде Солнца или Земли, и вычислить хорошо известную ньютоновскую силу гравитационного притяжения. В этом конкретном случае результаты не будут новыми, однако новым будет их значение. Вещество и энергия искривляют пространство-время, и это искривление порождает тяготение. Но общая теория относительности имеет дополнительное преимущество, состоящее в том, что она включает в распределение вещества и энергии любой тип энергии, в том числе энергию самого гравитационного поля. Теория становится полезной даже в тех ситуациях, когда сама гравитация вносит значительный вклад в энергию.
Так как уравнения Эйнштейна применимы к любому распределению энергии, они привели к изменению взглядов космологов — историков космоса. Теперь, если бы ученые знали содержащиеся во Вселенной вещество и энергию, они могли бы рассчитать ее эволюцию. В пустой Вселенной пространство будет совершенно пустым, без всякой ряби и неровностей, т. е. имеющим нулевую кривизну. Но когда Вселенную заполняет вещество и энергия, они искажают пространство-время, что влечет за собой интересные возможности для структуры Вселенной и ее изменения во времени.
Почти наверняка, мы не живем в статической Вселенной; как вскоре будет ясно, мы на самом деле должны жить в скрученной пятимерной вселенной. К счастью, общая теория относительности говорит нам, как рассчитать следствия этих гипотез. Так же как существуют примеры двумерных геометрий с положительной, нулевой и отрицательной кривизной, существуют и четырехмерные геометрические конфигурации пространства-времени с положительной, нулевой и отрицательной кривизной, которые могут возникать из соответствующих распределений вещества и энергии. В дальнейшем, когда мы будем обсуждать космологию и браны в дополнительных измерениях, критически важными будут искажения пространства-времени, возникающие от вещества и энергии, как в нашей видимой Вселенной, так и на бранах и в балке. Мы увидим, что три типа пространственно-временной кривизны (положительная, отрицательная и нулевая) могут также реализовываться в высших измерениях.
Общая теория относительности приводит к ряду следствий, которые нельзя рассчитать с помощью ньютоновской теории тяготения. Одним из многих преимуществ общей теории относительности является возможность устранить раздражающее понятие о действии на расстоянии ньютоновской теории, утверждающее, что гравитационное влияние тела будет ощущаться везде, как только это тело возникнет или начнет двигаться. Как мы знаем, согласно общей теории относительности, прежде чем гравитация может подействовать, пространство-время должно деформироваться. Этот процесс не происходит мгновенно. Он занимает время. Гравитационные волны распространяются со скоростью света. Гравитационные явления могут проявиться в данном месте только через промежуток времени, который нужен сигналу, чтобы дойти до этого места и исказить пространство-время. Этот интервал времени никогда не может быть меньше того интервала времени, который затрачивает свет, распространяющийся быстрее всего, что мы знаем, чтобы попасть в это место. Например, вы никогда не примете сигнал радио или мобильного телефона быстрее, чем через промежуток времени, который затрачивает световой пучок, чтобы долететь до вас.
Кроме того, физики сумели применить уравнения Эйнштейна для описания других типов гравитационного поля. С помощью общей теории относительности ученые смогли описать и изучить черные дыры. Эти поразительные таинственные объекты образуются тогда, когда вещество сильно сконцентрировано в очень малом объеме. Геометрия пространства-времени в черных дырах в высшей степени искажена, так что все, что попадает на черную дыру, захватывается внутрь. Даже свет не может вырваться наружу. Почти сразу после создания общей теории относительности Карл Шварцшильд обнаружил[47], что черные дыры являются следствием уравнений Эйнштейна. Однако лишь в 1960-е годы физики всерьез восприняли идею, что черные дыры могут реально существовать в нашей Вселенной. В наши дни черные дыры полностью признаются астрофизическим сообществом. На самом деле есть мнение, что в центре каждой галактики, включая нашу собственную, существует сверхмассивная черная дыра. Кроме того, если существуют скрытые измерения, то существуют и многомерные черные дыры, и если они велики, то выглядят как четырехмерные черные дыры, наблюдаемые астрономами.
Кода
Чтобы завершить историю с GPS, заметим, что для вычисления положения с точностью до 1 м необходимо измерять время с относительной точностью 10-13. Единственный возможный способ достичь такой точности — воспользоваться атомными часами.
Но даже если наши часы окажутся идеальными, благодаря эффекту замедления времени их ход будет замедляться на 10-10 в относительных единицах. Если такая ошибка не будет исправлена, она окажется в тысячу раз больше той, которая допустима для GPS. Кроме того, следует принять во внимание гравитационное голубое смещение — эффект общей теории относительности, связанный с тем, что фотон движется в изменяющемся гравитационном поле, и приводящий к ошибке по меньшей мере того же порядка. Эти и другие отклонения, связанные с общей теорией относительности, будут приводить к ошибкам, которые, если ими пренебречь, будут суммироваться, приводя к общей ошибке больше 10 км/день[48]. Икар (и современные GPS) должны вносить поправки, обусловленные этими релятивистскими эффектами.
Хотя к настоящему времени теория относительности хорошо проверена и даже предсказывает эффекты, которые необходимо учитывать в практических устройствах, мне кажется любопытным, что поначалу никто не услышал Эйнштейна. Он был совершенно неизвестным ученым, работавшим в патентном бюро Берна, так как не мог найти лучшей работы. Находясь в этом малопривлекательном месте, он предложил теорию, противоречившую взглядам всех остальных физиков того времени.
Джеральд Холтон, историк науки из Гарварда, рассказывал мне, что первым сторонником Эйнштейна стал немецкий физик Макс Планк. Если бы не Планк, немедленно отметивший блистательность работы Эйнштейна, могло бы потребоваться значительно больше времени на то, чтобы теория была замечена и принята. Вслед за Планком несколько других известных физиков оказались достаточно знающими, чтобы выслушать и обратить внимание на работу Эйнштейна. Вскоре это сделал весь мир.
Что стоит запомнить
• Скорость света постоянна. Она не зависит от скорости наблюдателя.
• Теория относительности изменяет наши представления о пространстве и времени и утверждает, что мы можем рассматривать их совместно как единую структуру пространство-время.
• Специальная теория относительности связывает значения энергии, импульса (указывающего нам, как тело откликается на действие силы) и массы. Например, E = mc2, где Е — энергия, m — масса и с — скорость света.
• Масса и энергия заставляют пространство-время искривляться, и можно понимать это искривленное пространство-время как источник гравитационного поля.
Глава 6
Квантовая механика: принципиальная неопределенность, главные неопределенности и соотношение неопределенностей
And you may ask yourself,
am I right?.. Am I wrong?
Talking Heads[49]
Икар никак не мог понять, то ли Афина заставляет его смотреть слишком много фильмов, то ли Дитер слишком много говорит о физике. Но какова бы ни была причина, прошлой ночью Икару приснилось, что он встретил квантового детектива. В длинном пальто и мягкой фетровой шляпе, с каменным выражением на лице, детектив из сна говорил:
«Я ничего не знал о ней, кроме ее имени и того, что она стояла передо мной. Но с того момента, как я посмотрел на нее, я понял, что с Электрой[50] будут проблемы. Когда я спросил ее, откуда она пришла, она отказалась отвечать, в комнате было две двери, так что она должна была войти через одну из них. Но Электра хрипло прошептала: „Мистер, забудьте это. Я никогда не скажу вам, через которую“.
Хотя я видел, что она вся трясется, я попытался припереть эту особу к стенке. Но Электра с бешеной скоростью задвигалась, как только я начал к ней приближаться. она молила меня не подходить ближе. Увидев ее волнение, я отступил. Хотя я не был новичком в вопросах неопределенности, в этот раз я был побежден, казалось, неопределенность собиралась еще какое-то время слоняться здесь».
Квантовая механика, несмотря на все свое противоречие интуиции, фундаментально изменила те пути, которыми ученые познают мир. На основе квантовой механики возникли многие разделы современной науки: в результате ее развития были либо созданы, либо пересмотрены статистическая механика, физика частиц, химия, космология, молекулярная биология, эволюционная биология и геология (в том, что касается радиоактивной датировки). Многие удобства современного мира, например компьютеры, DVD-проигрыватели и цифровые фотоаппараты, были бы невозможны без транзисторов и современной электроники, развитие которых основано на квантовых явлениях.
Я не уверена, что, впервые начав изучать квантовую механику в колледже, я полностью отдавала себе отчет в том, насколько она странна. Я изучила основные принципы и научилась применять их в разных условиях. Но только спустя многие годы, потраченные на изучение квантовой механики и тщательное обдумывание квантово-механической логики, я поняла, как фантастична эта наука. Хотя сейчас квантовая механика и включена в программу общефизического образования, она все равно остается поистине потрясающей.
История создания квантовой механики является замечательным примером того, как должна развиваться наука. На ранней стадии квантовая механика развивалась в духе построения моделей — она пыталась объяснить непонятные наблюдаемые эффекты до того, как кто-то озадачился сформулировать соответствующую теорию. И экспериментальные, и теоретические открытия происходили быстро и неистово. Физики развивали квантовую теорию для интерпретации экспериментальных результатов, которые не могла объяснить классическая физика. В свою очередь, квантовая теория предлагала новые эксперименты, с помощью которых можно было проверить гипотезы.
Ученым потребовалось время на то, чтобы осмыслить все следствия этих экспериментальных наблюдений. Для большинства вторжение квантовой механики оказалось слишком радикальным, чтобы немедленно принять эту науку. Ученые должны были отложить свои сомнения до того, как они могли признать идеи квантовой механики, столь отличающиеся от знакомых классических понятий. Даже такие корифеи теоретической физики, как Макс Планк, Эрвин Шрёдингер и Альберт Эйнштейн никогда до конца не перешли на квантовомеханический уровень мышления. Эйнштейн выразил свои возражения знаменитой фразой: «Бог не играет в кости со Вселенной». Большинство ученых в конце концов, но не сразу, признало истину (как мы сейчас ее понимаем).
Радикальная природа научных достижений в начале двадцатого века нашла отклик в современной культуре. Сразу же кардинально изменились основы искусства и литературы и наше понимание психологии. Хотя многие связывают эти достижения с потрясениями и разрушениями Первой мировой войны, художники, подобные Василию Кандинскому, использовали возможность проникновения вглубь атома для подтверждения идеи, что все может изменяться и поэтому в искусстве все разрешено. Кандинский так описывал свою реакцию на открытие ядра атома: «Крах модели атома был эквивалентен в моей душе краху всего мира. Внезапно рухнули самые толстые стены. Я не удивился бы, если бы камень, возникший перед моими глазами, растаял и стал невидимым» [51].
Конечно, реакция Кандинского была несколько чрезмерной. Легко обмануться, применяя столь же радикальные, как основы квантовой механики, суждения в ненаучном контексте. Мне кажется, что наиболее заезженным примером является частое злоупотребление соотношением неопределенностей, которое часто употребляется, чтобы оправдать неточность. Мы увидим в этой главе, что соотношение неопределенностей есть, на самом деле, очень точное утверждение, касающееся измеряемых величин. Тем не менее это утверждение имеет удивительные приложения.
Обратимся теперь к квантовой механике и лежащим в ее основе принципам, которые столь сильно отличаются от принципов ранее существовавшей старой, классической физики. Странные и новые понятия, с которыми мы столкнемся, включают квантование, волновую функцию, дуализм волна — частица и соотношение неопределенностей. В данной главе дано описание этих ключевых идей, приправленное рассказами об истории того, как это все создавалось.
Шок и страх
Специалист по физике частиц Сидни Коулмен говорил, что если тысячи философов проведут тысячи лет в поисках самой странной из возможных вещей, они не найдут ничего более фантастичного, чем квантовая механика. Эту науку трудно понять, так как ее следствия удивительны и сильно противоречат интуиции. Фундаментальные принципы квантовой механики противоречат как предпосылкам, лежащим в основе всей ранее известной физики, так и нашему собственному опыту.
Одна причина того, что квантовая механика кажется столь неестественной, заключается в том, что мы физиологически не готовы воспринимать квантовую природу вещества и света. В общем случае квантовые эффекты становятся существенными на расстояниях порядка одного ангстрема[52], т. е. порядка размера атома. Не используя специальные инструменты, мы можем видеть только предметы значительно больших размеров. Даже пиксели на экранах телевизоров высокого разрешения или мониторах компьютеров слишком малы для того, чтобы мы могли их видеть.
Кроме того, мы видим только громадные скопления атомов, настолько большие, что квантовые эффекты подавляются классическими. В общем случае мы также воспринимаем только большое количество квантов света. Хотя светочувствительные рецепторы в глазе достаточно чувствительны, чтобы воспринимать наименьшие возможные единицы света — отдельные кванты, глаз в типичной ситуации одновременно обрабатывает так много квантов, что любые возможные квантовые эффекты подавляются более легко различимым классическим поведением.
Существует очень простая причина того, что квантовую механику трудно объяснить. Квантовая механика достаточно всеобъемлюща, чтобы включать классические предсказания, но не наоборот. Во многих случаях, например, когда мы имеем дело с большими телами, квантово-механические предсказания согласуются с предсказаниями классической ньютоновской механики. Однако не существует какого-то интервала размеров, в котором классическая механика порождала бы квантовые предсказания. Поэтому, когда мы пытаемся понять квантовую механику, используя знакомые классические термины и понятия, мы быстро наталкиваемся на трудности. Попытка использовать классические понятия для описания квантовых эффектов похожа на попытку перевода французского текста с помощью ограниченного английского словаря, содержащего сто слов. Вы будете часто натыкаться на понятия или слова, смысл которых можно передать только приблизительно, или которые вообще невозможно перевести с помощью столь ограниченного английского словаря.
Датский физик Нильс Бор, один из пионеров квантовой механики, был уверен в неадекватности человеческого языка для описания внутреннего устройства атома. Размышляя над этим, он рассказывал, как его модели «пришли к нему интуитивно… как картинки»[53]. Другой физик, Вернер Гейзенберг, объяснял: «Мы просто должны помнить, что наш обычный язык больше не работает, что мы находимся в области физики, где наши слова мало что значат» [54].
Поэтому я не буду пытаться описывать квантовые явления с помощью классических моделей. Напротив, я опишу ключевые фундаментальные предположения и явления, которые столь отличают квантовую механику от созданных ранее классических теорий. Мы рассмотрим отдельно ряд ключевых наблюдений и идей, которые внесли вклад в развитие квантовой механики. Хотя это обсуждение будет примерно следовать историческим событиям, моя цель на самом деле состоит в том, чтобы одновременно ввести многие новые идеи и понятия, присущие квантовой механике.
Начало квантовой механики
Квантовая физика развивалась поэтапно. Она началась как ряд случайных предположений, согласующихся с наблюдениями, хотя никто не понимал причину согласия. Эти догадки, не имевшие соответствующего физического обоснования, но обладавшие способностью давать правильные ответы, образовали то, что сейчас именуется старой квантовой теорией. Она определялась предположением, что такие величины, как энергия и импульс, не могут принимать любые произвольные значения. Вместо этого была подтверждена возможность, что такие величины принимают дискретное, квантованное множество значений.
Квантовая механика, развившаяся из своей скромной предшественницы — старой квантовой теории, подтвердила загадочное предположение о квантовании, с которым мы вскоре столкнемся. Кроме того, с помощью квантовой механики была разработана определенная процедура для предсказания эволюции квантово-механических систем во времени, что весьма усилило предсказательную мощь теории. Однако поначалу квантовая механика развивалась только путем подгонок и резких скачков, так как в то время никто не понимал, что происходит. На первых порах все, что было — это предположения о квантовании.
Развитие старой квантовой теории началось в 1900 году, когда немецкий физик Макс Планк предположил, что свет может испускаться только квантованными порциями, подобно тому, как хлеб может продаваться только отдельными буханками. Согласно гипотезе Планка, количество энергии в свете любой заданной частоты может быть лишь целым кратным фундаментальной энергии для этой конкретной частоты. Фундаментальная энергия равна величине, известной сейчас как постоянная Планка h, умноженной на частоту f. Энергия света определенной частоты f может равняться hf, 2hf, 3hf и т. д., но согласно гипотезе Планка вы никогда не обнаружите значения энергии между указанными числами. В противоположность буханкам хлеба, квантование которых произвольно и нефундаментально (буханки можно раскрошить), существует минимальная порция энергии света данной частоты, являющаяся неделимой. Промежуточные значения энергии никогда не возникают.
Это удивительное пророческое предложение было сделано для того, чтобы разрешить теоретическую загадку, известную как ультрафиолетовая [55] катастрофа в излучении черного тела. Абсолютно черное тело — это объект вроде куска каменного угля, который поглощает все падающее на него излучение, а затем полностью излучает его обратно[56]. Количество световой и другой энергии, которое абсолютно черное тело испускает, зависит от его температуры; на самом деле температура полностью определяет все физические свойства абсолютно черного тела.
Однако классические предсказания для количества света, испускаемого черным телом, выглядели сомнительными: классические вычисления предсказывали, что излучение высоких частот должно уносить значительно большую энергию, чем наблюдали и фиксировали физики. Измерения показывали, что вклад излучения разных частот в излучение абсолютно черного тела не подчиняется законам демократии; очень высокие частоты вносят меньший вклад, чем более низкие частоты. Основная доля энергии излучается только на низких частотах. Именно поэтому светящиеся тела нагреты «до красного», а не до «голубого каления». Однако классическая физика предсказывает значительную долю излучения высоких частот. Более того, по классическим предсказаниям полная испущенная энергия должна быть бесконечно большой. Классическая физика столкнулась лицом к лицу с ультрафиолетовой катастрофой.
Возможный способ разрешения этой дилеммы заключался бы в предположении, что вклад в излучение абсолютно черного тела могут вносить только частоты ниже некоторого верхнего предела. Планк отверг эту возможность в пользу другого, в равной степени произвольного предположения, что свет квантован.
Планк полагал, что если излучение на каждой частоте состоит из целых кратных фундаментального кванта излучения, то излучение высоких частот не может испускаться, так как фундаментальная единица энергии была бы слишком большой. Так как энергия, содержащаяся в кванте света, пропорциональна частоте, то даже один квант высокочастотного излучения содержал бы значительное количество энергии. Когда частота достаточно велика, минимальная энергия, которую содержал бы квант, оказывается слишком большой, для того, чтобы квант излучился. Абсолютно черное тело может и спускать только кванты малых частот. Таким образом, гипотеза Планка запрещает излучение слишком больших частот.
Логику рассуждений Планка может пояснить следующая аналогия. Наверное, вам приходилось обедать в ресторане с людьми, которые в конце трапезы не заказывали десерт. Эти люди боятся съесть слишком много калорийной пищи, поэтому они редко себя балуют сладкими блюдами. Если официант обещает, что десертное блюдо маленькое, они могут заказать одну порцию. Но они обычно пасуют перед большой порцией кекса, мороженого или пудинга.
Такие люди делятся на две категории. К первой принадлежит Икар. Он соблюдает режим и действительно не употребляет десерт. Когда подают слишком большой десерт, Икар просто воздерживается от этого блюда. Я отношусь, скорее, ко второй категории людей (к ним относится и Афина), которые понимают, что десерты слишком велики, и поэтому не заказывают их для себя, но в противоположность Икару без всяких угрызений совести берут по маленькому кусочку от десертов на блюдах других гостей. Таким образом, даже когда Афина не заказывает порцию для себя, она в результате как следует наедается десертами. Если бы Афина обедала вместе с большим числом людей и могла бы стянуть кусочки с большого числа тарелок, она бы пострадала от плачевной «калорийной катастрофы».
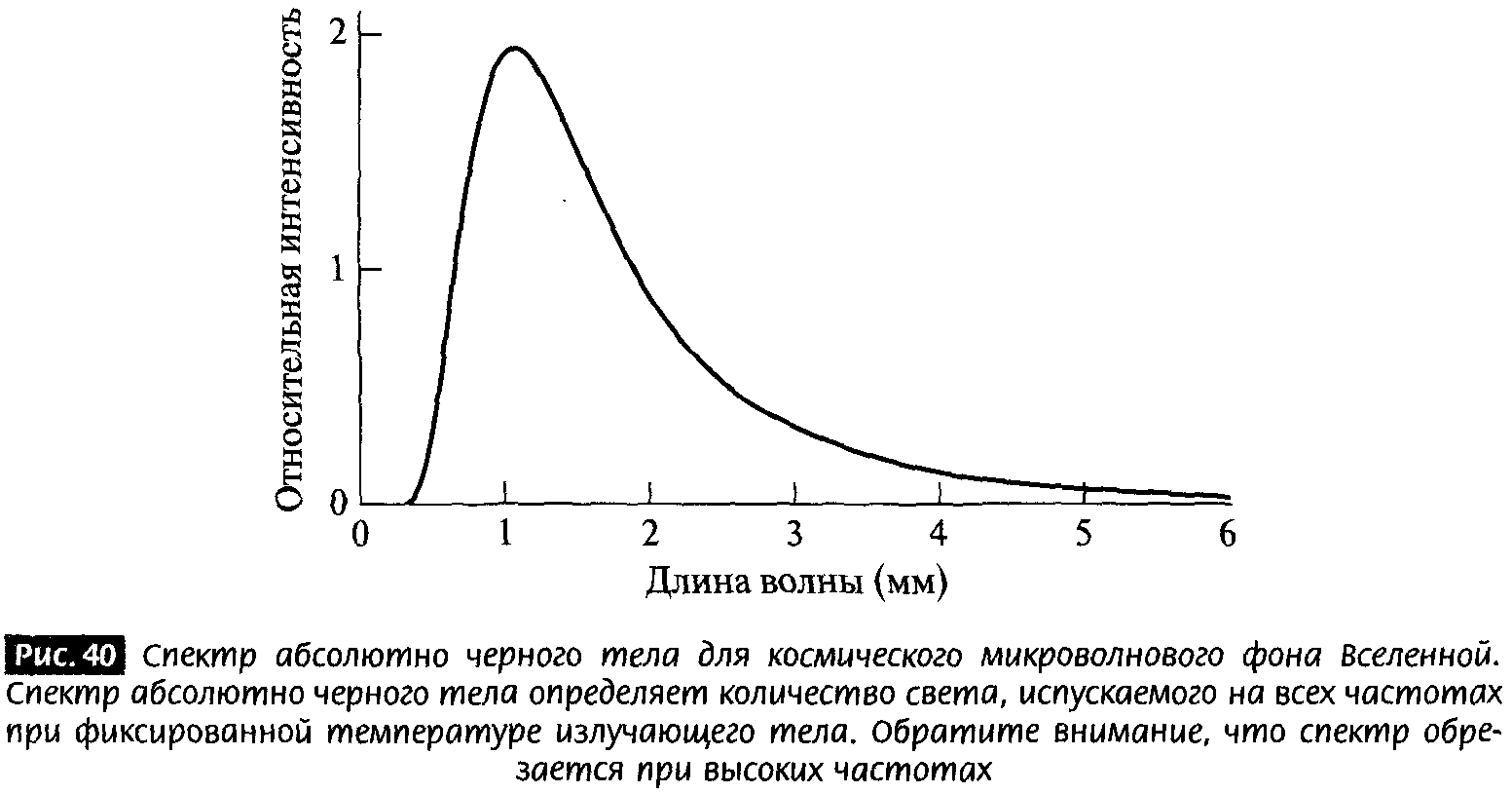
Согласно классической теории, абсолютно черное тело больше похоже на Афину. Оно испускало бы малые порции света любой частоты, и теоретики, используя классические рассуждения, неизбежно предсказали бы «ультрафиолетовую катастрофу». Чтобы избежать такого предсказания, Планк предположил, что абсолютно черное тело аналогично по-настоящему умеренному в еде человеку. Как и Икар, который никогда не ест ни кусочка десерта, абсолютно черное тело ведет себя согласно закону квантования Планка и испускает свет данной частоты только квантованными порциями энергии, равными константе h, умноженной на частоту света f. Если частоты большие, квант энергии станет просто слишком большим для того, чтобы свет мог испуститься на этой частоте. Таким образом, абсолютно черное тело будет испускать основную часть излучения на малых частотах, а большие частоты будут автоматически отброшены. В квантовой теории абсолютно черное тело не испускает заметного количества высокочастотного излучения, и поэтому испускает заметно меньше излучения, чем предсказывается классической теорией.
Когда тело испускает излучение, то структура этого излучения, т. е. количество энергии, испускаемой телом на каждой частоте при заданной температуре, называется спектром этого излучения (рис. 40). Спектры некоторых тел, например звезд, могут быть приближенно описаны спектром абсолютно черного тела. Такие чернотельные спектры были измерены при многих конкретных значениях температуры, и все они согласуются с гипотезой Планка. На рис. 40 видно, что излучение почти полностью приходится на низкие частоты, а при высокой частоте оно выключается.
Одним из великих достижений экспериментальной космологии после 1980-х годов было все более точное измерение чернотельного спектра, порождаемого излучением в нашей Вселенной. Первоначально Вселенная была горячим, плотным огненным шаром, содержащим высокотемпературное излучение, однако с тех пор Вселенная расширилась и излучение очень сильно охладилось. Это произошло потому, что при расширении Вселенной точно так же растягивались и длины волн излучения. Но волны большей длины соответствуют более низким частотам, а следовательно и более низким температурам. Сейчас Вселенная содержит излучение, которое выглядит так, как будто оно было порождено излучением абсолютно черного тела с температурой 2,7 градуса выше абсолютного нуля, что существенно холоднее, чем в начале расширения.
Недавно с помощью спутников был измерен спектр этого космического фонового микроволнового излучения (именно он показан на рис. 40). Он почти точно совпадает со спектром абсолютно черного тела температурой 2,7 К. Измерения показывают, что отклонения меньше одной десятитысячной. На самом деле такое реликтовое излучение является в наши дни наиболее точно измеренным спектром абсолютно черного тела.
Когда в 1931 году Планка спросили, как он пришел к своему поразительному предположению о том, что свет квантован, он ответил: «Это был акт отчаяния. В течение шести лет я бился над теорией абсолютно черного тела. Я понимал, что проблема фундаментальна, и я знал ответ. Мне нужно было любой ценой[57]… найти теоретическое объяснение». Для Планка квантование света было инструментом, кладжем[58], приводящим к правильному спектру абсолютно черного тела. По его мнению, квантование не было обязательно свойством самого света, а могло быть следствием какого-то свойства атомов, излучающих свет. Хотя предположение Планка было первым шагом к пониманию квантования света, сам Планк никогда полностью не принимал этой гипотезы.
Пять лет спустя, в 1905 году, большой вклад в квантовую теорию внес Эйнштейн, который установил, что световые кванты были реальностью, а не просто математическими абстракциями. В тот год Эйнштейн был очень занят, одновременно занимаясь построением специальной теории относительности, помогая доказать существование атомов и молекул путем изучения статистических свойств вещества и предоставляя подтверждение квантовой теории, и все это в то время, когда он работал в патентном бюро в швейцарском городе Берне.
Конкретное явление, которое Эйнштейн объяснил с помощью гипотезы о световых квантах, тем самым усилив ее достоверность, известно как фотоэлектрический эффект. Экспериментаторы облучают вещество излучением определенной частоты, и это падающее излучение выбивает из вещества электроны. Экспериментаторы показали, что облучение вещества большим количеством света, несущим больше полной энергии, не изменяет максимальной кинетической энергии (энергии движения) испущенных электронов. Это противоречит интуитивному представлению: большая падающая энергия должна безусловно порождать электроны с большей кинетической энергией. Почему же электроны не поглощают больше энергии?
Объяснение Эйнштейна заключалось в том, что излучение состоит из отдельных квантов света, и только отдельный квант может передать свою энергию любому конкретному электрону. Свет падает на отдельный электрон как одиночный снаряд, а не как множество снарядов при массированном обстреле. Так как только один квант света выбивает электрон, увеличение числа падающих квантов не изменяет энергию испущенного электрона. Увеличение числа падающих квантов приводит к тому, что свет выбивает больше электронов, но не влияет на максимальную энергию любого отдельно взятого электрона.
Поскольку Эйнштейн интерпретировал результаты фотоэффекта с помощью понятия об определенных порциях энергии — квантах света, стало понятным, почему испускаемые электроны всегда обладают одинаковой максимальной кинетической энергией. Наибольшая кинетическая энергия, которую может иметь электрон, равна постоянной энергии, которую он получает от кванта света, за вычетом энергии, необходимой для испускания электрона атомом.
Рассуждая таким образом, Эйнштейн сумел вычислить энергию квантов света. Он показал, что их энергия зависит от частоты падающего света точно так, как предсказывала гипотеза Планка. Для Эйнштейна это было ясным свидетельством реальности существования квантов. Его интерпретация давала очень точную картину световых квантов: один квант испытывал соударение с одним электроном, который по этой причине испускался. Именно это открытие, а не теория относительности, принесло Эйнштейну Нобелевскую премию по физике 1921 года.
Поразительно, однако, что хотя Эйнштейн признавал существование квантованных порций света, он с большой неохотой соглашался с тем, что эти кванты на самом деле были безмассовыми частицами, переносившими энергию и импульс, но не имевшими массы. Первое убедительное свидетельство корпускулярной природы квантов света было получено в 1923 году при наблюдении эффекта Комптона, в котором в результате соударения кванта света с электроном происходило изменение направления движения этого кванта (рис. 41). В общем случае можно определить энергию и импульс частицы, измерив ее угол отклонения после соударения. Если фотоны — безмассовые частицы, то они должны совершенно определенным образом вести себя после соударения с другими частицами, например электронами. Измерения показали, что кванты света ведут себя в точности так, как если бы они были безмассовыми частицами, взаимодействующими с электронами. Неизбежным был вывод: кванты света действительно являются частицами. Сейчас мы называем их фотонами.
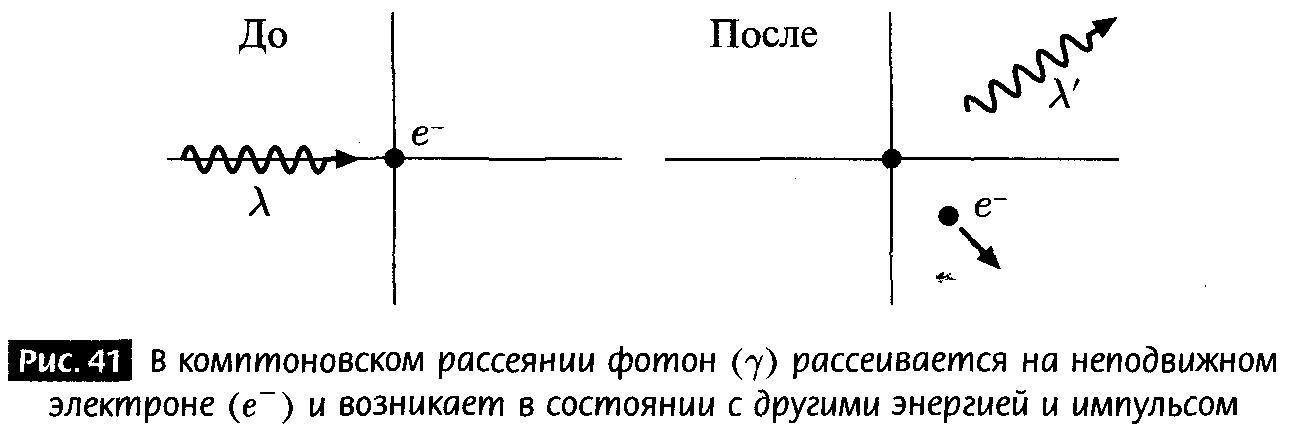
Интересно, что Эйнштейн так сопротивлялся признанию квантовой теории, которую он же и помогал создать. Однако его реакция не более удивительна, чем недоверчивая реакция Планка на гипотезу Эйнштейна о квантовании. Планк и ряд других ученых хвалили многие достижения Эйнштейна, но умеряли свой энтузиазм[59]. Планк даже заметил несколько пренебрежительно: «Не следует ставить ему в упрек то, что он иногда промахивался в своих рассуждениях, например, в гипотезе о световых квантах, так как невозможно предложить действительно новые идеи даже в самых точных науках, если не пойти на некоторый риск»[60]. Но не заблуждайтесь. Предложенные Эйнштейном световые кванты были точным попаданием в цель. Замечание Планка всего лишь отражает революционную природу мышления Эйнштейна и изначальное сопротивление ученого сообщества принятию его идей.
Квантование и атом
История квантования и старая квантовая теория не закончились на изучении света. Оказалось, что вся материя состоит из фундаментальных квантов. Следующим ученым, внесшим вклад в гипотезу квантования, был Нильс Бор. Он применил эту гипотезу к хорошо известной частице — электрону.
Частично интерес Бора к квантовой механике развился из знакомства с попытками прояснить загадочные свойства атомов. В течение девятнадцатого века понятие об атоме было неправдоподобно смутным: многие ученые вообще не верили в то, что атомы существуют иначе как полезный эвристический прием, не имеющий никакого реального основания. Некоторые ученые, верившие в атомы, тем не менее путали их с молекулами, которые, как сейчас известно, состоят из атомов.
Истинные свойства и строение атомов оставались неизвестными вплоть до начала прошлого века. Частично проблема состояла в том, что греческое слово ατομο означает «неделимый», так что первоначальная картина атома действительно представляла некоторый неизменный, неделимый объект. Но физики девятнадцатого века, изучая поведение атомов, начали понимать, что такая картина неверна. В конце XIX века самыми подробно изученными свойствами атомов были радиоактивность и спектральные линии — характерные частоты испускания и поглощения света. Оба эти явления показывали, что атомы могут изменяться. Вершиной этих изысканий стало открытие Дж. Дж. Томсоном в 1897 году электронов. Он также высказал гипотезу, что электрон является частью атома, откуда следовало, что атомы должны быть делимы.
В начале XX века Томсон объединил все известные к тому времени наблюдения над атомами, создав модель «сливового пудинга», получившую название от английского десерта, в котором в тесто добавлялись целые кусочки фруктов. По мнению Томсона, в атоме имелась положительно заряженная часть, распределенная по всему атому (тесто), и вкрапленные отрицательно заряженные электроны (кусочки фруктов).
В 1910 году новозеландец Эрнест Резерфорд доказал, что эта модель неверна, после того как Ганс Гейгер и студент-исследователь Эрнест Марсден осуществили предложенный Резерфордом эксперимент. Они обнаружили внутри атома твердое, компактное ядро, которое было намного меньше самого атома. Образующийся при радиоактивном распаде солей радия газ радон-222 испускает альфа-частицы, являющиеся, как мы сейчас знаем, ядрами гелия. Физики получили доказательство существования атомного ядра, обстреливая атомы альфа-частицами и регистрируя углы, на которые альфа-частицы отклоняются. Зарегистрированное учеными удивительное рассеяние могло возникнуть только при условии, что внутри атома имеется твердое, компактное атомное ядро. Рассеянный положительный заряд, размазанный по всему объему атома, никогда не мог бы отклонять частицы на столь большие углы. Говоря словами Резерфорда: «Это было самое невероятное событие из всех, когда либо случавшихся в моей жизни. Это было столь же невероятно, как если бы вы выстрелили 15-дюймовым снарядом в кусок папиросной бумаги, и снаряд отскочил бы назад и попал в вас» [61].
Результаты Резерфорда опровергли модель атома в виде сливового пудинга. Его эксперимент означал, что положительный заряд не размазан по всему атому, а сосредоточен в значительно меньшей внутренней сердцевине. Должно было существовать твердое центральное ядро. Согласно такой картине, атом состоит из электронов, вращающихся по орбитам вокруг маленького центрального ядра.
Летом 2002 года я принимала участие в ежегодной конференции по теории струн, которая проводилась в тот год в Кэвендишской лаборатории в Кембридже. Многие основоположники квантовой механики, в том числе два ведущих ученых Резерфорд и Томсон, совершили большую часть своих исследований в этих стенах. Коридоры украшены воспоминаниями о волнующих первых годах, так что гуляя по ним, я узнала много забавных фактов.
Например, Джеймс Чедвик, первооткрыватель нейтрона, стал заниматься физикой только потому, что не смог перебороть свою застенчивость и признаться, что при выборе дисциплин он ошибочно отметил в заявлении не ту строчку. Когда Дж. Дж. Томсон стал руководителем лаборатории, он был так молод (ему было двадцать восемь лет), что в одном из поздравлений было написано: «Прости меня, что не написал, что желаю тебе счастья и успехов в должности профессора. Новость о твоем избрании стала для меня большим сюрпризом, и я не смог». (Физики не всегда бывают самыми милосердными.)
Однако несмотря на согласованную картину атома, развитую в начале двадцатого века в Кэвендишской и других лабораториях, поведение составных частей атома было таково, что оно могло разрушить наиболее фундаментальные убеждения физиков. Из опытов Резерфорда следовала модель атома, состоящего из электронов, движущихся по орбитам вокруг центрального атомного ядра. Несмотря на простоту этой картины, она, к сожалению, имела один недостаток: она должна была быть ошибочной. Классическая теория электромагнетизма предсказывает, что когда электроны движутся по окружности, они должны излучать энергию за счет испускания фотонов (или, на классическом языке, излучения электромагнитных волн). Таким образом, фотоны уносят энергию, оставляя все меньше энергии электрону, который будет обращаться пе все меньшим окружностям, по спирали приближаясь к центру. На самом деле классическая теория электромагнетизма предсказывает, что атомы не могут быть стабильными и должны коллапсировать за время меньше одной наносекунды. Стабильные электронные орбиты в атоме были полной загадкой. Почему электроны не теряют энергию и не падают по спирали на атомное ядро?
Для объяснения орбит электронов в атоме потребовался радикальный отход от классического образа мышления. Доведение такой логики до неизбежного вывода выявило прорехи в классической физике, которые могли быть устранены только в результате развития квантовой механики. Нильс Бор сделал именно такое революционное предположение, расширив планковское понятие о квантовании и перенеся его на электроны. Это стало существенным компонентом старой квантовой механики.
Квантование электронов
Бор предположил, что электроны не могут двигаться ни по одной из старых орбит; электронная орбита должна иметь радиус, определяющийся предложенной Бором формулой. Бор сумел открыть эти орбиты благодаря удачной и остроумной гипотезе. Он предположил, что электроны должны вести себя так, как будто они являются волнами, откуда следует, что, обращаясь вокруг ядер, они колеблются вверх и вниз.
В общем случае некоторая волна совершает однократное колебание вверх и вниз при прохождении определенного пути; этот путь и называется длиной волны. С волной, бегущей по окружности, также связана длина волны. В этом случае длина волны определяет величину дуги, вдоль которой при обращении вокруг ядра волна проходит один раз вверх и вниз.
Электрон, вращающийся по орбите определенного радиуса, не может иметь произвольную длину волны. Он может иметь только такую длину волны, которая позволит ей совершить колебания вверх и вниз определенное число раз. Отсюда возникает правило для определения разрешенных длин волн: проходя по окружности, определяющей орбиту электрона, волна должна совершить целое[62] число колебаний (рис. 42).

Хотя предложение Бора было радикальным, а его смысл туманным, оно достигало своей цели: если принять такую гипотезу, она гарантирует стабильность орбит электрона. Оказываются разрешенными только определенные орбиты электронов. Промежуточные орбиты запрещены. В отсутствие внешнего посредника, который мог бы заставить электрон перепрыгнуть с одной орбиты на другую, у электрона не было других возможностей приблизиться к ядру.
Можно представить себе атом Бора с фиксированными электронными орбитами как многоэтажное здание, в котором можно находиться только на четных этажах — втором, четвертом, шестом и т. д. Так как вы никогда не сможете ступить ногой на промежуточные этажи, например, третий или пятый, вы будете вечно приклеены к тому четному этажу, на котором находитесь. У вас нет возможности попасть на самый нижний этаж и выйти наружу.
Волны Бора представляли собой вдохновенную гипотезу. Бор не утверждал, что понимает смысл этих волн; он выдвинул свою гипотезу просто для того, чтобы получить стабильные электронные орбиты. Тем не менее количественная природа гипотезы Бора позволяла осуществить ее проверку. В частности, гипотеза Бора правильно предсказывала спектральные линии атомов. Спектральные линии определяют частоту света, который испускает или поглощает неионизированный атом, т. е. нейтральный атом со всеми своими электронами и полным зарядом, равным нулю[63]. Физики заметили, что вместо того, чтобы показывать непрерывное распределение (в которое дают вклад все длины волн света), спектры демонстрировали напоминающую штрих-код структуру из отдельных полос. Никто не мог понять причину этого. Более того, никто не мог объяснить точные значения наблюдавшихся частот.
Опираясь на свою гипотезу квантования, Бор сумел объяснить, почему фотоны испускались или поглощались только с наблюдавшимися частотами. Хотя у изолированного атома электронные орбиты были стабильны, они могли изменяться, если фотон с нужной частотой и, следовательно, согласно Планку, с нужной энергией, передавал или отбирал энергию.
Используя рассуждения, основанные на классической физике, Бор вычислил энергию электронов, подчинявшихся его гипотезе квантования. Зная эти энергии, он предсказал энергии, а следовательно, и частоты фотонов, которые испускает или поглощает атом водорода, обладающий одним электроном. Предсказания Бора оказались правильными, и поэтому его гипотеза квантования стала весьма правдоподобной. Именно это убедило ученых, среди которых был и Эйнштейн, что Бор должен быть прав.
Квантованные световые пакеты, которые могут испускаться или поглощаться и тем самым изменять орбиты электронов, можно сравнить с длинами веревок, протянутых между окнами многоэтажного здания в нашем предыдущем примере. Если каждый кусок веревки имеет точно ту длину, которая нужна, чтобы перебраться с вашего этажа на любой другой четный этаж, и если открыты только окна на четных этажах, то веревка позволит меняться этажами, но только с четными номерами. Аналогично, длины волн спектральных линий могут принимать только определенные значения, равные разностям энергий электронов, занимающих дозволенные орбиты.
Несмотря на то что Бор не дал объяснения своему условию квантования, он оказался безусловно прав. Были измерены длины волн многих спектральных линий, и всех их можно было воспроизвести с помощью гипотезы Бора. Если такое согласие считать случайным совпадением, это можно рассматривать как чудо. В конце концов квантовая механика подтвердила гипотезу Бора.
Отход от частиц
Как бы ни были важны правила квантования, квантово-механическая связь между частицами и волнами стала укрепляться только после исследований французского физика герцога Луи де Бройля, австрийца Эрвина Шрёдингера и немца по происхождению Макса Борна.
Первым ключевым шагом от случайного блуждания по тропам старой квантовой теории к выходу на дорогу истинной квантово-механической теории было замечательное предложение де Бройля перевернуть гипотезу квантования Планка с ног на голову. В то время как Планк связывал кванты с волнами излучения, де Бройль, как и Бор, постулировал, что частицы также ведут себя как волны. Гипотеза де Бройля состояла в том, что частицы должны проявлять волновые свойства, и эти волны определяются импульсом частицы. (При малых скоростях импульс частицы равен произведению ее массы и скорости. При всех скоростях импульс указывает, каким образом нечто реагирует на приложенную силу. Хотя при релятивистских скоростях импульс является более сложной функцией массы и скорости, обобщение импульса, применимое при больших скоростях, также указывает, каким образом нечто реагирует на действие силы при релятивистских скоростях.)
Де Бройль предположил, что частица с импульсом р связана с волной, длина которой обратно пропорциональна импульсу, т. е. чем меньше импульс, тем больше длина волны. Кроме того, длина волны пропорциональна постоянной Планка h [64]. Идея, лежавшая в основе гипотезы де Бройля, состояла в том, что бурно колеблющаяся волна (длина волны которой мала) переносит больший импульс, чем волна, колеблющаяся как в летаргическом сне (с большой длиной волны). Меньшим длинам волн соответствуют более быстрые осцилляции, которые де Бройль сопоставил с большими импульсами.
Если вы ошарашены существованием такой частицы-волны, именно так и должно быть. Когда де Бройль впервые ввел понятие о своих волнах, никто не знал, что это такое. Макс Борн предложил удивительную интерпретацию: волна есть функция координаты, и квадрат этой функции определяет вероятность обнаружения частицы в каком-то месте пространства[65]. Борн назвал эту функцию волновой функцией. Идея Макса Борна заключалась в том, что невозможно зафиксировать положение частиц, и его можно описывать только с помощью вероятностей. Это огромный шаг в сторону от классических представлений. Это означает, что вы не можете знать точное местоположение частицы. Вы можете только определить вероятность ее обнаружения в каком-то месте.
Однако несмотря на то, что квантово-механическая волна описывает только вероятности, сама квантовая механика предсказывает точную эволюцию этой волны во времени. Задавая значения волны в любой данный момент времени, можно определить ее значения в любой последующий момент. Шрёдингер написал волновое уравнение, описывающее эволюцию волны, связанной с квантовомеханической частицей.
Но что означает эта вероятность обнаружения частицы? Идея представляется загадочной — в конце концов, такого понятия, как доля частицы, не существует. Утверждение, что частицу можно описывать волной, было (и в определенном смысле остается) одним из самых удивительных свойств квантовой механики, в частности, потому что известно, что частицы часто ведут себя как бильярдные шары, а не как волны. Интерпретации на языке частиц и волн кажутся несовместимыми.
Разрешение кажущегося парадокса тесно связано с тем, что с помощью только одной частицы вы никогда не установите ее волновую природу. Когда вы детектируете отдельный электрон, вы видите его в некотором определенном месте. Чтобы отобразить всю волну, вам требуется либо множество тождественных электронов, либо многократное повторение одного и того же эксперимента. Даже несмотря на то что каждый электрон связан с волной, с помощью одного электрона можно измерить только одно число. Но если вы могли бы подготовить большую совокупность тождественных электронов, вы обнаружили бы, что доля электронов в каждом месте пропорциональна вероятности, которую приписывает электрону квантовая механика.
Волновая функция отдельного электрона говорит нам о вероятном поведении многих тождественных электронов, описываемых одной и той же волновой функцией. Любой отдельный электрон будет обнаружен только в одном месте. Но если имеется много тождественных электронов, их распределение по разным местам будет подобно волне. Волновая функция определяет вероятность попадания электрона в одно из этих мест.
Можно провести аналогию с распределением населения по росту. Каждый индивидуум имеет свой рост, но распределение говорит нам о вероятности того, что индивидуум имеет определенный рост. Аналогично, если один электрон ведет себя как частица, много электронов вместе будут иметь распределение по положениям, схематически изображаемое волной. Различие состоит в том, что отдельный электрон, тем не менее, связан с этой волной.
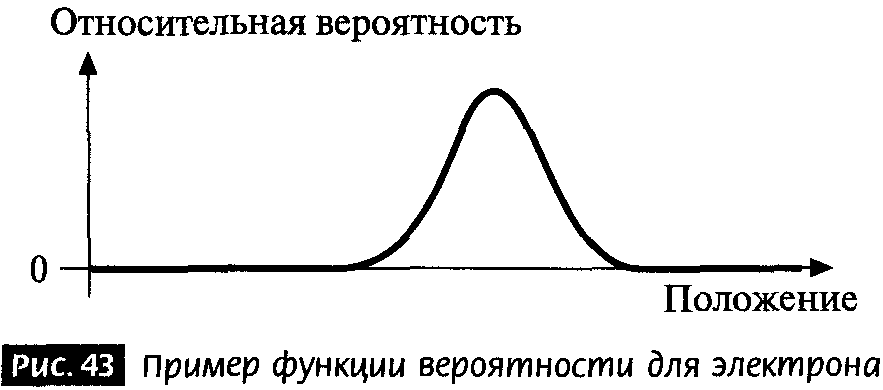
На рис. 43 я набросала пример функции вероятности для электрона. Эта волна изображает относительную вероятность обнаружения электрона в конкретном месте. Нарисованная мной кривая принимает определенное значение в каждой точке пространства (или, скорее, на линии, так как бумага плоская, и я вынуждена изображать только одно измерение пространства). Если бы я могла сделать много копий этого электрона, я могла бы совершить серию измерений положения электрона. Тогда я обнаружила бы, что количество раз, когда я находила электрон в определенной точке, было бы пропорционально этой функции вероятности. Большим значениям соответствовало бы то, что электрон с большей вероятностью был бы найден в этой точке, меньшим значениям — что он был бы найден в этой точке с меньшей вероятностью. Волна отражает кумулятивный эффект многих электронов.
Даже несмотря на то, что вы отобразили волну с помощью многих электронов, уникальной особенностью квантовой механики является то, что отдельный электрон все равно тоже описывается волной. Это означает, что вы никогда

не можете ничего предсказать об электроне с определенностью. Если вы измеряете положение электрона, вы обнаруживаете его в определенном месте. Но пока вы не совершите это измерение, вы можете только предсказать, что электрон с определенной вероятностью должен находиться где-то в окрестности. Вы не можете точно сказать, где он остановится.
Корпускулярно-волновой дуализм обнаруживается в знаменитом эксперименте с двумя щелями, на который ссылается неизвестный собеседник Электры в начале этой главы. До 1961 года, когда немецкий физик Клаус Йонссон реально осуществил этот эксперимент в лаборатории, опыт с двумя щелями был скорее мысленным экспериментом, использовавшимся физиками для уяснения смысла и следствий поведения волновой функции электрона. Экспериментальная установка состоит из источника электронов, который посылает электроны сквозь барьер, в котором прорезаны две параллельные щели (рис. 44). Электроны проходят через щели, попадают на расположенный за барьером экран и регистрируются.
Подразумевалось, что этот эксперимент будет подобен эксперименту, выполненному в начале XIX века и продемонстрировавшему волновую природу света. В том эксперименте британский физик, врач и египтолог[66] Томас Юнг направил монохроматический свет сквозь две щели и наблюдал волновую картину, созданную светом на экране за щелями. Опыт Юнга продемонстрировал, что свет ведет себя как волна. Смысл повторения такого же эксперимента с электронами состоял в том, чтобы увидеть, как можно было бы наблюдать волновую природу электрона.
Действительно, если вы осуществите эксперимент с двумя щелями с электронами, вы увидите то же самое, что Юнг увидел для света — волновую картину на экране за щелями (рис. 45). В случае света мы понимаем, что волны интерферируют. Какая-то часть света проходит через одну щель, какая-то — через другую, и регистрируемая волновая картина отражает интерференцию между двумя волнами. Но что означает волновая картина для электронов?
Такая волновая картина на экране свидетельствует о полностью противоречащем нашей интуиции факте: мы должны считать, что каждый электрон проходит через обе щели. Вы не можете знать все об отдельном электроне. Любой электрон может пройти через обе щели. Даже несмотря на то, что положение каждого электрона в момент попадания на экран фиксируется, никто не знает, через которую из двух щелей проходит каждый отдельный электрон.
Квантовая механика утверждает, что частица может перемещаться от начальной точки до конечной по любому возможному пути, и этот факт отражает волновая функция частицы. В этом состоит одно из многих удивительных свойств квантовой механики. Вопреки классической физике, квантовая механика не приписывает частице определенную траекторию.

Но каким образом эксперимент с двумя щелями может указывать, что отдельный электрон ведет себя как волна, когда мы уже знаем, что электроны — это частицы? Ведь в конце концов не существует такой вещи, как половинка электрона. Каждый отдельный электрон фиксируется в определенном месте. Что же на самом деле происходит?
Ответ был уже дан мною выше. Вы можете наблюдать волновую картину, только зарегистрировав много электронов. Каждый отдельный электрон является частицей. Он попадает в определенное место на экране. Однако совокупный эффект многих электронов, падающих на экран, представляет собой классическую волновую картину, отражая тот факт, что пути двух электронов интерферируют. Это показано на рис. 45.
Волновая функция определяет вероятность того, что электрон попадет на экран в любом заданном месте. Электрон может попасть в любое место, но мы ожидаем обнаружить его в некотором определенном месте с определенной вероятностью, задаваемой значением волновой функции в данной точке. Совокупность многих электронов образует волну, которую можно рассчитать, исходя из предположения, что электрон проходит через обе щели.
В 1970-х годах Акира Тонамура в Японии и Пьерджорджо Мерли, Джулио Поцци и Джанфранко Миссироли в Италии смогли явно наблюдать этот эффект в реальных экспериментах. Они выстреливали электроны по одному и наблюдали, как создается волновая картина по мере того, как все больше электронов попадают на экран.
Вас может удивить, почему потребовалось дожить до двадцатого века, чтобы заметить нечто столь выдающееся, как корпускулярно-волновой дуализм. Например, почему люди не поняли раньше, что свет выглядит как волна, но на самом деле состоит из крохотных зернышек — фотонов?
Ответ состоит в том, что никто из нас (за возможными редкими исключениями, касающимися супергероев) не видит отдельных фотонов[67], так что квантовомеханические эффекты нелегко детектировать. Обычный свет не выглядит так, как будто он состоит из отдельных квантов. Мы наблюдаем пучки фотонов, образующих видимый свет. Большое число фотонов действует совместно, как классическая волна.
Чтобы непосредственно наблюдать квантовую природу света, необходим очень слабый источник фотонов или очень аккуратно настроенная аппаратура. Когда фотонов слишком много, вы не можете различить эффект от каждого из них по отдельности. Добавление еще одного фотона к классическому свету, состоящему из большого числа фотонов, не составляет большой разницы. Если лампочка в вашем доме, ведущая себя классически, испустит один дополнительный фотон, вы никогда этого не заметите. Наблюдать тонкие квантовые явления можно только с помощью тщательно разработанной аппаратуры.
Если вы не верите в то, что последний фотон обычно несуществен, подумайте о том, как вы себя чувствуете, когда идете голосовать. Вы знаете, что ваш голос вряд ли может изменить картину, если учесть голоса миллионов других людей, так что ваше голосование представляется потерей времени и хлопотами. Если не считать известного исключения во Флориде, штате неопределенности, обычно один голос теряется в общей куче. Даже несмотря на то что выбор осуществляется за счет совокупного учета отдельных голосов, один голос редко изменяет результат. (Проводя сравнение еще на шаг дальше, вы можете заметить, что только в квантовых системах, и во Флориде, которая ведет себя как квантовый штат[68], повторяющиеся измерения приводят к разным результатам.)
Неопределенность Гейзенберга
Волновая природа материи влечет за собой много противоречащих интуиции следствий. Перейдем от неопределенности на выборах к соотношению неопределенностей Гейзенберга, любимой теме бесед физиков и послеобеденных ораторов.
Немецкий физик Вернер Гейзенберг был одним из главных создателей квантовой механики. В своей автобиографии[69] он рассказывает, что когда в 1919 году он с товарищами был размещен в здании семинарии в Мюнхене и участвовал в борьбе с баварскими коммунистами, у него в голове начали рождаться первые революционные идеи об атомах и квантовой механике. Когда затихала стрельба, он залезал на крышу семинарии и читал диалоги Платона, в частности, «Тимей». Сочинения Платона убедили Гейзенберга, что «для того, чтобы интерпретировать материальный мир, нам необходимо что-то знать о его мельчайших составных частях».
Гейзенберг ненавидел внешние потрясения, сопровождавшие его в молодости; он предпочел бы возврат к «принципам прусской жизни, подчинению индивидуальных амбиций общему делу, скромности в личной жизни, честности и неподкупности, благородству и точности»[70]. Тем не менее, сформулировав соотношение неопределенностей, Гейзенберг безвозвратно изменил взгляды людей на мир. Вероятно, бурная эпоха, в которую жил Гейзенберг, породила в нем революционный подход если не к политике, то к науке2. Во всяком случае, мне кажется несколько забавным, что автор соотношения неопределенностей был человеком столь противоречивых взглядов.
Соотношение неопределенностей утверждает, что есть определенные пары величин, которые никогда не могут быть точно измерены в один и тот же момент времени. Это стало главным отличием от классической физики, в рамках которой предполагается, что, по крайней мере в принципе, все характеристики физической системы, например, координату и импульс, можно измерить с любой желаемой точностью.
Конкретные пары — это те, для которых имеет значение, какая из величин измеряется первой. Например, если вы измерили сначала положение, а затем импульс частицы (величина, определяющая как величину скорости, так и ее направление), вы получите другой результат по сравнению с тем, если сначала измеряется импульс, а затем положение. Такое невозможно в классической физике, и это, безусловно, отличается от того, к чему мы привыкли. Порядок измерений имеет значение только в рамках квантовой механики. И соотношение неопределенностей утверждает, что для двух величин, порядок измерения которых имеет значение, произведение их неопределенностей будет всегда больше, чем фундаментальная константа, а именно, постоянная Планка h (для самых любопытных, эта константа равна 6,582 · 10-25 ГэВ · с)3. Если вы настаиваете на том, чтобы знать очень точно положение частицы, вы не можете знать с той же точностью импульс, и наоборот. Не имеет значения, насколько точны ваши измерительные приборы и сколько раз вы повторяете измерения, — вы никогда не сможете одновременно измерить обе величины с очень большой точностью.
Появление постоянной Планка в соотношении неопределенностей имеет глубокий смысл. Постоянная Планка — это величина, возникающая только в квантовой механике. Напомним, что согласно квантовой механике квант энергии частицы с определенной частотой равен постоянной Планка, умноженной на эту частоту. Если бы миром правила классическая физика, постоянная Планка была бы равна нулю, и не было бы фундаментального кванта энергии.
Однако в истинном квантово-механическом описании мира постоянная Планка есть фиксированная, ненулевая величина. Именно это число характеризует неопределенность. В принципе любая отдельная величина может быть точно известна. Иногда физики, чтобы описать ситуацию, когда некоторая величина точно измерена и поэтому принимает точное значение, говорят о коллапсе волновой функции. Слово «коллапс» относится к форме волновой функции, которая уже не размыта, а принимает ненулевое значение в одном конкретном месте, так как вероятность получения при последующем измерении любого другого значения равна нулю. В этом случае, когда одна величина измерена точно, соотношение неопределенностей утверждает, что после измерения вы не можете знать вообще ничего о другой величине, образующей пару с измеренной величиной в соотношении неопределенностей. Вы получите бесконечную неопределенность значения этой другой величины. Конечно, если бы вы сначала измерили вторую величину, то первая величина стала бы для вас неизвестной. Иными словами, чем точнее вы знаете одну из величин, тем менее точным должно быть измерение другой.
Я не буду в этой книге углубляться в подробный вывод соотношения неопределенностей, однако попытаюсь тем не менее дать представление о его происхождении. Так как это несущественно для последующего изложения, вы можете сразу перейти к следующему разделу. Но, может быть, кому-то из вас захочется чуть больше узнать о тех рассуждениях, которые лежат в основе соотношения неопределенностей.
В этом выводе мы сосредоточимся на соотношении неопределенностей время — энергия, которое чуть легче объяснить и понять. Это соотношение связывает неопределенность энергии (и следовательно, согласно гипотезе Планка, частоты) с интервалом времени, характерным для скорости изменения системы. Иными словами, произведение неопределенности энергии и характерного времени изменения системы всегда будет больше постоянной Планка h.
Физическая реализация соотношения неопределенностей время — энергия возникает, например, когда вы включаете в комнате лампу и слышите помехи в находящемся рядом радиоприемнике. Включение света генерирует радиочастоты в большом интервале. Происходит это потому, что ток, идущий по проводам, изменяется очень быстро, так что интервал энергии (следовательно, частоты) должен быть большим. Ваш радиоприемник ловит эти частоты как радиопомехи.
Чтобы понять происхождение соотношения неопределенностей, рассмотрим совершенно другой пример — протекающий водопроводный кран[71]. Мы покажем, что для точного определения скорости протечки крана нужен длительный процесс измерения, и это очень похоже на то, что утверждает соотношение неопределенностей. Кран и вода, идущая через него, содержат много атомов и являются слишком сложной системой для того, чтобы проявлять наблюдаемые квантово-механические эффекты, — они подавляются классическими процессами. Тем не менее верно, что для более точного определения частоты требуются более долгие измерения, а в этом и состоит суть соотношения неопределенностей. Квантово-механическая система делает еще шаг вперед в рассмотрении этой взаимозависимости, так как для тщательно приготовленной квантово-механической системы энергия и частота связаны между собой. Так, для квантово-механической системы связь между неопределенностью частоты и длительностью времени измерения (подобная той, которую мы собираемся рассмотреть) переводится в истинное соотношение неопределенностей между энергией и временем.
Предположим, что вода капает со скоростью примерно одна капля в секунду. С какой точностью можно измерить скорость вытекания воды, если точность вашего секундомера равна одной секунде, т. е. его показания могут отличаться от точных не более чем на одну секунду? Если вы подождете одну секунду и увидите одну каплю, вы можете подумать, что вправе сделать вывод, будто кран капает со скоростью одна капля в секунду.
Однако, так как ваш секундомер может показывать время с точностью одна секунда, ваше наблюдение не позволит точно установить, сколько времени проходит, пока кран капнет. Если ваши часы один раз тикнули, прошедшее время может быть чуть больше одной секунды, или почти равняться двум секундам. В какой же момент времени между одной и двумя секундами вы должны считать, что кран капнул? Без более точного секундомера или без увеличения времени измерений ответа не найти. С имеющимися у вас часами вы можете заключить, что капли падают со скоростью в интервале от одной капли в секунду до одной капли в две секунды. Если вы заявите, что кран капает один раз в секунду, вы можете по существу сделать 100 %-ную ошибку в своих измерениях. Иначе говоря, вы можете ошибиться в два раза.
Но предположим, что вы ждете 10 секунд, осуществляя свое измерение. Тогда за время, пока ваши часы тикнули 10 раз, из крана капнули 10 капель. Если пользоваться вашим плохим секундомером, точность которого равна 1 секунде, все, что вы можете утверждать, это то, что время, которое потребовалось на появление 10 капель, находится в интервале от 10 до 11 секунд. Ваше измерение, которое опять приведет к утверждению, что капли падают примерно по одной в секунду, будет теперь иметь ошибку лишь 10 %. Это происходит потому, что, ожидая 10 секунд, вы можете измерить частоту появления капель с точностью 1/10 секунды. Обратите внимание, что произведение времени вашего измерения (10 секунд) и неопределенности в частоте (10 % или 0,1) примерно равно 1. Заметьте также, что произведение неопределенностей в частоте и времени для измерения в первом примере, когда ошибка в измерении частоты (100 %) больше, но измерение занимает меньшее время (1 секунда), также порядка 1.
Можно было бы продолжать в том же духе. Если вы совершаете измерение в течение 100 секунд, вы можете измерить частоту падения капель с точностью 1 капля за 100 секунд. Если вы совершаете измерение в течение 1000 секунд, вы можете измерить частоту падения капель с точностью 1 капля за 1000 секунд. Во всех этих случаях произведение интервала времени, в течение которого вы производите измерение, и точности, с которой вы измеряете частоту, примерно равно 1[72]. Для более точного измерения частоты требуется большее время. Это утверждение лежит в основе соотношения неопределенностей между временем и энергией. Вы можете более точно измерить частоту, но для этого нужно проводить измерения дольше. Произведение времени и неопределенности в частоте всегда порядка 1[73].
Чтобы завершить вывод нашего упрощенного соотношения неопределенностей, заметим, что если вы рассматриваете достаточно простую квантово-механическую систему, например отдельный фотон, ее энергия будет равна постоянной Планка h, умноженной на частоту. Для такого объекта произведение интервала времени, в течение которого вы производите измерения энергии, и неточности в энергии всегда будет превышать h. Вы можете измерить энергию системы с любой желаемой точностью, но ваш эксперимент будет длиться соответственно большее время. Это то же самое соотношение неопределенностей, которое мы только что вывели; дополнительный трюк — всего лишь соотношение квантования, связывающее энергию и частоту.
Два важных значения энергии и что о них говорит соотношение неопределенностей
Мы почти завершили наше введение в основы квантовой механики. В этом и следующем разделах мы рассматриваем два оставшихся элемента квантовой механики, которые будут использоваться в дальнейшем.
В этом разделе не содержится никаких новых физических принципов, а представлено одно важное приложение соотношения неопределенностей и специальной теории относительности. Рассматриваются соотношения между двумя важными значениями энергии и наименьшими масштабами длины физических процессов, которые могут чувствовать частицы с такими энергиями. Физики каждодневно используют эти соотношения. В следующем разделе мы введем спин, бозоны и фермионы — понятия, которые появятся в следующей главе, посвященной Стандартной модели физики частиц, и далее, когда мы будем рассматривать суперсимметрию.
Соотношение неопределенностей для положения и импульса утверждает, что произведение неопределенностей положения и импульса должно быть больше, чем постоянная Планка. Оно утверждает, что нечто, будь то пучок света, частица или любой другой объект или система, которые вы можете представить, чувствительное к физическим процессам, происходящим на малых расстояниях, должно включать большой интервал импульсов (так как неопределенность импульса должна быть весьма велика). В частности, любой объект, чувствительный к таким физическим процессам, должен включать очень большие импульсы. Согласно специальной теории относительности, когда велики импульсы, то велики и энергии. Комбинация этих двух фактов указывает, что единственный способ исследования малых расстояний — использование для этого больших энергий.
Другой способ объяснения — сказать, что большие энергии для изучения малых расстояний нужны нам потому, что в физических процессах на малых расстояниях участвуют только частицы, волновые функции которых меняются на малых расстояниях. Так же как Вермеер не смог бы написать свои картины с помощью кисти шириной два дюйма, и так же как вы не можете видеть мелкие детали, если у вас плохое зрение, частицы не могут быть чувствительными к физическим процессам на малых расстояниях, если их волновые функции не меняются на очень малых масштабах. Но, согласно де Бройлю, частицы, волновые функции которых включают малые длины волн, обладают большими импульсами. Де Бройль утверждал, что длина волны частицы-волны обратно пропорциональна ее импульсу. Поэтому соотношение де Бройля вынуждает нас заключить, что для анализа физических явлений на малых расстояниях нужны частицы с большими импульсами, а следовательно, и большими энергиями.
Этот вывод имеет важные следствия для физики частиц. Только частицы больших энергий чувствуют явления, связанные с физическими процессами на малых расстояниях. Рассмотрим на двух конкретных примерах, насколько большие энергии подразумеваются.
Физики-частичники часто измеряют энергию в числах, кратных электрон-вольту (сокращенно эВ). Один электронвольт равен энергии, требуемой для движения электрона в поле с разностью потенциалов 1 В (такую разность потенциалов создает слабенькая батарейка). Я буду далее использовать производные единицы гигаэлектронвольт (ГэВ) и тераэлектронвольт (ТэВ); 1 ГэВ равен 1 миллиарду эВ, 1 ТэВ равен 1 триллиону эВ.
Физики-частичники часто находят удобным использовать эти единицы для измерения не только энергии, но и массы. Это можно сделать, так как соотношения между массой, импульсом и энергией в специальной теории относительности показывают, что эти три величины связаны друг с другом скоростью света — константой, значение которой равно с = 299 792 458 м/с. С помощью скорости света можно перевести данную энергию в массу или импульс. Например, знаменитая формула Эйнштейна Е = тс2 означает, что с каждой конкретной энергией связана определенная масса. Так как каждый знает, что переводной коэффициент равен с2, его можно убрать, и выразить все массы в единицах эВ. В таких единицах масса протона равна примерно 1 миллиарду эВ или 1 ГэВ.
Такой перевод одних единиц в другие аналогичен тому, что вы делаете каждый день, говоря, например, кому-то: «Станция в десяти минутах от нас». Вы предполагаете известным конкретный переводной коэффициент. Расстояние может быть равным одному километру, что соответствует десяти минутам ходьбы пешком, или двадцати километрам, что соответствует десяти минутам езды по скоростной дороге. Между вами и вашим собеседником существует негласная договоренность о согласованном переводном коэффициенте.
Эти соотношения специальной теории относительности в сочетании с соотношением неопределенностей определяют минимальный пространственный размер физических процессов, который может исследовать или детектировать волна или частица определенной энергии или массы. Применим эти соотношения к двум очень важным в физике частиц энергиям, которые часто будут появляться в последующих главах (рис. 46).
Первая энергия, известная как характерная энергия слабых взаимодействий, равна 250 ГэВ. Физические процессы при этой энергии определяют ключевые свойства слабого взаимодействия и элементарных частиц, наиболее интересным из которых является механизм приобретения частицами массы. Физики (включая меня) ожидают, что, когда мы исследуем эту область энергии, обнаружатся новые явления, предсказываемые пока что неизвестными физическими теориями, и мы узнаем много нового о фундаментальной структуре материи. К счастью, эксперименты уже близки к исследованию области характерной энергии слабых взаимодействий и вскоре смогут рассказать нам все, что мы хотим знать.
Иногда я буду говорить о характерной массе слабых взаимодействий, которая связана с энергией слабых взаимодействий через скорость света. В более привычных единицах характерная масса слабых взаимодействий равна 10-24 кг. Но, как я уже объясняла, физики-частичники предпочитают говорить о массе в единицах ГэВ.
Связанный с энергией радиус слабых взаимодействий равен 10-18 м. Он определяет размер сферы действия слабого взаимодействия — максимальное расстояние, на котором частицы могут влиять друг на друга за счет сил слабого взаимодействия.
Так как соотношение неопределенностей утверждает, что малые расстояния можно исследовать только с помощью больших энергий, радиус слабых взаимодействий является также минимальной длиной, которую может прощупать частица с энергией 250 ГэВ, т. е. это есть минимальный масштаб, на который могут повлиять физические процессы с такой энергией. Если бы с помощью этой энергии можно было исследовать меньшие расстояния, неопределенность в расстоянии была бы меньше 10-18 м, и соотношение неопределенностей между расстоянием и импульсом было бы нарушено. Работающий в настоящее время ускоритель в Фермилабе[74] и будущий Большой адронный коллайдер (БАК), строительство которого завершается в ЦЕРНе в Женеве, будут исследовать физические процессы вплоть до этого масштаба, и многие модели, которые я буду обсуждать в этой книге, должны иметь при такой энергии наблюдаемые следствия.
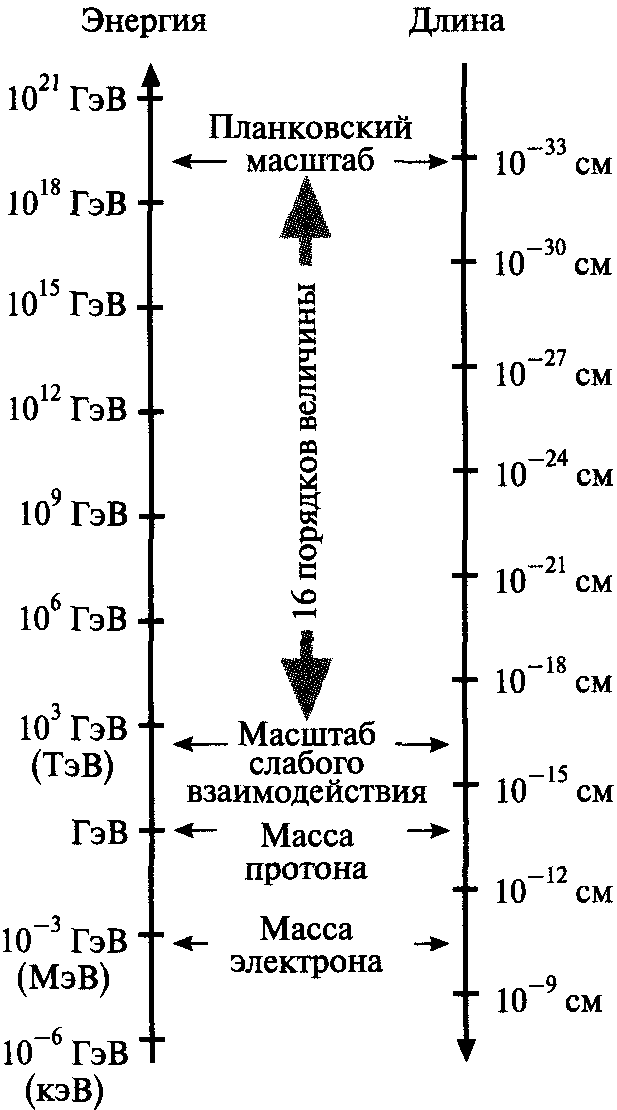

Вторая важная энергия, известная как платовская энергия МPl, равна 1019 ГэВ. Эта энергия имеет большое отношение к любой теории тяготения. Например, гравитационная постоянная, входящая в закон тяготения Ньютона, обратно пропорциональна квадрату планковской энергии. Из-за того, что планковская энергия очень велика, гравитационное притяжение двух масс мало.
Кроме того, планковская энергия — наибольшая возможная энергия, для которой можно применять классическую теорию тяготения; выше этой энергии существенной становится квантовая теория гравитации, последовательно описывающая как квантовую механику, так и тяготение. Ниже, при обсуждении теории струн, мы увидим также, что в старых моделях теории струн натяжение струны скорее всего определяется планковской энергией.
Квантовая механика и соотношение неопределенностей утверждают, что когда частицы достигают этой энергии, то с их помощью можно исследовать физические процессы, происходящие на расстояниях порядка планковской длины, равной 10-35 м. Это расстояние невероятно мало, много меньше расстояния, доступного измерению. Но для описания физических процессов, возникающих на столь малых расстояниях, требуется квантовая теория гравитации, и такой теорией может быть теория струн. По этой причине планковская длина, так же как и планковская энергия, являются важными масштабами, которые будут часто появляться в последующих главах.
Бозоны и фермионы
Квантовая механика указывает на важное различие между частицами, разделяя весь мир частиц на бозоны и фермионы. Эти частицы могут относиться к фундаментальным, например, электроны и кварки, или к составным, таким как протон или атомное ядро. Любой объект является либо бозоном, либо фермионом.
Является ли такой объект бозоном или фермионом, зависит от свойства, называемого внутренним спином частицы. Название наводит на определенные образы[75], однако спин частиц не соответствует никакому реальному движению в пространстве. Однако если частица имеет внутренний спин, она взаимодействует с другими так, как будто на самом деле вращается, несмотря на то что на самом деле никакого вращения нет.
Например, взаимодействие электрона с магнитным полем зависит от классического вращения электрона, его реального вращения в пространстве. Однако взаимодействие электрона с магнитным полем зависит также от внутреннего спина электрона. В противоположность классическому моменту импульса, возникающему из-за реального движения в физическом пространстве[76], внутренний спин является свойством частицы. Он фиксирован и обладает определенным значением сейчас и всегда. Например, фотон есть бозон со спином 1 (в единицах h). Это свойство фотона, оно столь же фундаментально, как тот факт, что фотон движется со скоростью света.
В квантовой механике спин квантован. Квантовый спин может принимать значения 0 (т. е. полное отсутствие спина), 1, 2 или любое целое число единиц спина. Объекты, называемые бозонами по имени индийского физика Сатиендры Ната Бозе, имеют внутренний спин, т. е. квантово-механический спин, не зависящий от вращения, принимающий целые значения: бозоны могут иметь внутренний спин, равный 0, 1, 2 и т. д.
Спин фермионов квантован в единицах, о которых до развития квантовой механики никто и не мог подумать, что они возможны. Фермионы, названные по имени итальянского физика Энрико Ферми, имеют полуцелые значения внутреннего спина, например, 1/2 или 3/2. В то время как объект со спином 1 возвращается к своей начальной конфигурации после однократного поворота вокруг своей оси, частицы спина 1/2 делает это только после двукратного поворота. Несмотря на кажущуюся фантастичность полуцелых значений спина, протоны, нейтроны и электроны все являются фермионами спина 1/2.
Фермионная структура самых фундаментальных частиц определяет многие свойства окружающего нас вещества. В частности, принцип Паули утверждает, что два фермиона одного типа никогда не могут находиться в одном и том же месте. Именно благодаря принципу исключения атом приобретает структуру, на которой основана вся химия. Так как электроны одинакового спина не могут находиться в одном и том же месте, они обязаны находиться на разных орбитах.
Именно поэтому я смогла выше провести аналогию с разными этажами высокого здания. Различные этажи представляют разные возможные квантованные орбиты, которые согласно принципу Паули заняты находящимися вокруг ядра электронами. Принцип исключения является также причиной того, что вы не можете просунуть руку сквозь крышку стола или упасть в центр Земли. Стол и ваша рука представляют жесткую структуру только потому, что соотношение неопределенностей порождает атомную, молекулярную и кристаллическую структуру вещества. Электроны в вашей руке тождественны электронам в столе, так что когда вы бьете рукой по столу, электронам не находится внутри стола места. Никакие два тождественных фермиона не могут находиться в одном и том же месте в одно и то же время, так что вещество не может просто разрушиться.
Бозоны действуют в точности противоположным образом. Они могут находиться и находятся в одном и том же месте. Бозоны напоминают крокодилов, которые предпочитают скапливаться друг на друге. Если вы включите свет в помещении, где свет уже есть, то его поведение будет существенно отличаться от ударов каратиста рукой по столу. Свет, состоящий из являющихся бозонами фотонов, беспрепятственно проходит сквозь другой свет. Два световых пучка могут светить точно в одном месте. В действительности, на этом основаны лазеры: занимающие одно и то же состояние бозоны позволяют лазерам создавать сильные когерентные пучки. Сверхтекучие жидкости и сверхпроводники также состоят из бозонов.
Экстремальным примером свойств бозонов является бозе-эйнштейновский конденсат, в котором много тождественных частиц коллективно ведут себя как одна частица. Такое поведение совершенно невозможно у фермионов, которые должны находиться в разных местах. Бозе-эйнштейновские конденсаты возможны только потому, что бозоны, из которых они состоят, в противоположность фермионам могут иметь совершенно одинаковые свойства. В 2001 году Эрик Корнелл, Вольфганг Кеттерле и Карл Виман получили Нобелевскую премию по физике за открытие бозе-эйнштейновского конденсата.
В дальнейшем мне не потребуются все эти подробности поведения бозонов и фермионов. Единственные факты, которые я буду использовать из этого раздела, таковы: фундаментальные частицы имеют внутренний спин и могут действовать так, как будто они вращаются вокруг своей оси в том или другом направлении, и все частицы являются либо бозонами, либо фермионами.
Что стоит запомнить
• Квантовая механика утверждает, что и вещество, и свет состоят из дискретных единиц — квантов. Например, кажущийся непрерывным свет на самом деле состоит из отдельных квантов, называемых фотонами.
• Кванты являются основой физики частиц. Стандартная модель физики частиц, объясняющая известные свойства материи и сил, утверждает, что вся материя и все силы могут быть в конечном итоге сведены к частицам и их взаимодействиям.
• Кроме того, согласно квантовой механике каждой частице сопоставляется волна, называемая волновой функцией частицы. Квадрат этой волны равен вероятности того, что частица будет обнаружена в определенном месте. Для удобства я буду иногда говорить о волне вероятности, равной квадрату более часто употребляемой волновой функции. Значения этой волны вероятности будут непосредственно определять сами вероятности. Такая волна появится позднее, когда мы будем обсуждать гравитон — частицу, которая передает силу тяготения. Волна вероятности важна и при обсуждении мод Калуцы — Клейна (КК), представляющих собой частицы, импульс которых направлен вдоль дополнительных измерений, т. е. перпендикулярно к обычным измерениям.
• Другое важное отличие квантовой механики от классической физики состоит в том, что квантовая механика утверждает, что вы не можете точно определить путь частицы — никогда нельзя знать точную траекторию частицы, соединяющую начальную и конечную точки. Отсюда следует, что мы должны рассматривать все пути, по которым может двигаться частица под действием силы. Так как квантовые пути могут включать любые взаимодействующие частицы, квантово-механические эффекты могут оказывать влияние на массы и константы взаимодействия.
• Квантовая механика делит частицы на бозоны и фермионы. Существование двух разных категорий частиц критически важно для структуры Стандартной модели, а также для предполагаемого расширения Стандартной модели, известного как суперсимметрия.
• Соотношение неопределенностей в квантовой механике в сочетании с соотношениями специальной теории относительности утверждает, что с помощью физических констант можно связать массу, энергию и импульс частицы с минимальным размером области, в которой частица данной энергии может испытывать силы или взаимодействия.
• Два из самых часто используемых приложений этих соотношений включают две энергии, известные как характерная энергия слабых взаимодействий и планковская энергия. Энергия слабых взаимодействий равна 250 ГэВ, а планковская энергия намного больше и составляет 1019 ГэВ.
• Только силы, радиус которых меньше 10-19 м, будут вызывать измеримые эффекты при воздействии на частицу с характерной энергией слабых взаимодействий. Это расстояние очень мало, но оно имеет отношение к физическим процессам в ядре и к механизму, с помощью которого частица приобретает массу.
• Несмотря на свою малость, радиус слабых взаимодействий намного больше планковской длины, равной 10-35 м. Это размер области, в которой силы оказывают влияние на частицы, обладающие планковской энергией. Такая энергия определяет интенсивность гравитационного взаимодействия. Это энергия, которую должны иметь частицы, чтобы гравитационное притяжение между ними стало сильным.
III Физика элементарных частиц
Глава 7
Стандартная модель физики частиц: самая фундаментальная из всех известных структура материи
You’re never alone,
You’re never disconnected!
You’re home with your own;
When company’s expected, you’re well protected!
… When you’re a jet, you stay a jet!
Riff («West Side Story»)[77]
Из всех прочитанных Афиной сказок ее больше всего поразила сказка Ганса Христиана Андерсена «Принцесса на горошине». В сказке рассказывается о принце, который безуспешно пытался найти подходящую принцессу, на которой он мог бы жениться. После того как он несколько недель тщетно занимался поисками, случайно в его дворец попала настоящая принцесса, искавшая укрытия от непогоды. Таким образом, эта насквозь промокшая гостья, ничего не подозревая, подверглась проверке, придуманной Королевой-матерью для принцесс.
Королева приготовила постель, на которую навалила высокую кучу матрасов и стеганых одеял, в самом низу под матрас она положила одну горошину, вечером Королева проводила свою гостью в заботливо приготовленную спальню. На следующее утро девушка (а она была настоящая принцесса) пожаловалась, что совершенно не могла спать. Она всю ночь металась и крутилась, а наутро обнаружила, что вся в синяках. Всему причиной была мешавшая ей горошина. Королева и Принц убедились, что их гостья действительно королевской крови, так как кто еще мог быть такой нежной!
Афина много раз прокручивала в голове эту сказку. Ей казалось очень странным, что кто-то, пусть даже самая чувствительная из принцесс, способен обнаружить горошину, лежа спокойно на горе из матрасов. После многодневных размышлений Афина нашла подходящее объяснение и кинулась к брату, чтобы все ему рассказать.
Афина отвергла обычную интерпретацию, что принцесса якобы доказала свое королевское происхождение, продемонстрировав изнеженность и утонченность, когда почувствовала нечто столь маленькое, как горошина под грудой матрасов. Она предложила другое объяснение.
Афина предположила, что когда Королева вышла из спальни, оставив принцессу в одиночестве, та отбросила все внешние приличия и дала волю своей бурной молодой натуре. Прежде чем улечься и попытаться заснуть, принцесса стала бегать по комнате и до изнеможения прыгать на кровати. Во время своих буйств принцесса сплющивала матрасы так, что на короткое время горошина выпирала сквозь них, образуя болезненный выступ, который и приводил к небольшому синяку. Афина не отрицала, что принцесса все же была довольно чувствительной, но полагала, что ее ревизионистская интерпретация намного лучше.
Обнаружение субструктуры внутри атома было столь же впечатляющим достижением, как и обнаружение горошины принцессой. Частицы, называемые кварками и являющиеся строительными блоками, из которых состоит протон, занимают примерно ту же долю объема протона, как и горошина в матрасе. Горошина объемом 1 см3 занимает одну миллионную долю матраса объемом 2 м х 1 м х 0,5 м, что не слишком отличается от доли объема, которую кварк занимает в протоне. Тот способ, которым физики обнаружили кварки, напоминает открытие буйной принцессы. Пассивная принцесса никогда бы не обнаружила горошину, погребенную под кучей слоев. Аналогично, физики не могли обнаружить кварки до тех пор, пока они не запустили в протон энергичными частицами, которые могли исследовать его внутренности.
В этой главе вы совершите скачок в Стандартную модель физики частиц — ту теорию, которая описывает известные элементарные составляющие материи и действующие между ними силы[78]. Стандартная модель, представляющая кульминацию многих удивительных и волнующих открытий является достижением огромной важности. Вам не требуется запоминать все детали, позднее я повторю названия всех существующих в природе частиц и природу их взаимодействий. Но Стандартная модель лежит в основе многих экзотических многомерных теорий, которые я опишу ниже, и когда вы познакомитесь с современными достижениями, знакомство со Стандартной моделью и ее ключевыми идеями приведет к более глубокому пониманию фундаментальной структуры материи и тех взглядов на мир, которых придерживаются физики в наши дни.
Электрон и электромагнетизм
Когда Владимир Ильич Ленин в философском труде «Материализм и эмпириокритицизм», используя в качестве метафоры электрон, писал, что «электрон… неисчерпаем», он имел в виду уровни теоретических идей и способ их интерпретации. Действительно, сейчас мы понимаем электрон совершенно не так, как это было в начале двадцатого века, до того, как квантовая механика перевернула наше понимание.
Но с точки зрения физики верно как раз противоположное утверждение: электрон исчерпаем. Насколько мы сейчас знаем, электрон является фундаментальным и неделимым. Для физика-частичника электрон не обладает «неисчерпаемой» структурой, а является простейшей частицей, которую описывает Стандартная модель. Электрон стабилен и не содержит внутри себя составных частей, так что мы можем полностью описать его, перечислив только несколько свойств, включая массу и заряд. (Чешский антикоммунист и специалист в области теории струн Любош Мотль насмешливо заметил, что это не единственное различие между его взглядами и взглядами Ленина.)
Электрон движется к положительно заряженному аноду батареи. Движущийся электрон реагирует на магнитную силу: когда электрон движется сквозь магнитное поле, его траектория искривляется. Оба эти явления есть результат наличия у электрона отрицательного заряда, благодаря которому электрон отзывается на электрические и магнитные силы.
До 1800-х годов все полагали, что электричество и магнетизм представляют собой совершенно разные силы. Однако в 1818 году датский физик и философ Ханс Эрстед обнаружил, что ток движущихся зарядов порождает магнитное поле. Из этого наблюдения он вывел, что должна существовать единая теория, описывающая как электричество, так и магнетизм: эти две силы должны быть двумя сторонами одной медали. Когда стрелка компаса реагирует на вспышку молнии, это явление подтверждает вывод Эрстеда.
Используемая и в наши дни классическая теория электромагнетизма была развита в XIX веке, опираясь на наблюдения о связи электричества и магнетизма. Критичным для этой теории явилось понятие поля. Поле — это название, данное физиками любой величине, пронизывающей все пространство. Например, значение гравитационного поля в любой точке пространства указывает нам, насколько сильно в этой точке проявляется тяготение. То же самое верно для поля любого типа: значение поля в каждом месте определяет, насколько интенсивно поле в этом месте.
В середине XIX века английский химик и физик Майкл Фарадей ввел понятия электрического и магнитного полей[79], и эти понятия сохранились в физике до наших дней. Заметим, что в четырнадцать лет Фарадей должен был временно прервать обучение в школе, чтобы помочь содержать семью. Поэтому вызывает восхищение тот факт, что ему удалось выполнить физические исследования столь революционного содержания. К счастью для Фарадея (и для истории физики) он был отдан в ученики к переплетчику, который поощрял его к чтению книг, над которыми работал, что позволяло Фарадею заниматься самообразованием.
Идея Фарадея состояла в том, что заряды создают электрические или магнитные поля всюду в пространстве, а эти поля, в свою очередь, действуют на другие заряды, независимо от того, где они находятся. Однако величина влияния электрических и магнитных полей на заряженные тела зависит от их местоположения. Поле оказывает наибольшее влияние на заряды в тех местах, где его величина максимальна, и наименьшее влияние там, где его величина минимальна.
Вы можете воочию убедиться в существовании магнитного поля, рассыпав железные опилки вблизи от постоянного магнита. Опилки соберутся в структуры в соответствии с напряженностью и направлением поля. Вы можете также изучать поле, удерживая два магнита близко друг от друга. Вы ощутите их взаимное притяжение или отталкивание задолго до того, как магниты соприкоснутся. Каждый магнит отзывается на поле, пронизывающее пространство между ними.
Вездесущность электрических полей окончательно дошла до меня в тот день, когда я завершала восхождение на гребень горы вблизи Боулдера (штат Колорадо) со спутником, который был новичком в этом деле, но имел значительный опыт пеших походов. Приближалась электрическая буря, я не хотела, чтобы мой спутник нервничал, поэтому попросила его двигаться побыстрее, не сказав, что связывающий нас трос потрескивает, а волосы моего спутника стоят дыбом. Когда мы благополучно спустились вниз и стали с удовольствием вспоминать наше путешествие, которое было в основном было приятным, мой спутник сказал, что он, конечно, понимал, что мы находимся в опасности: было видно, что мои волосы тоже стояли дыбом! Электрическое поле было не только в одном месте, оно было везде вокруг нас.
До XIX века никто не описывал электричество и магнетизм, пользуясь понятием поля. Для описания электрических и магнитных сил ученые обычно использовали понятие действия на расстоянии. Вероятно, в школе вам встречался термин действие на расстоянии для описания того, каким образом электрически заряженное тело мгновенно притягивается или отталкивается от любого другого заряда независимо от того, где он находится[80]. Это не кажется странным, так как именно к этому мы привыкли. Однако представляется невероятным, если нечто, находящееся в одном месте, могло бы мгновенно повлиять на другое тело, находящееся на некотором расстоянии. Каким образом передается информация о явлении?
Хотя может показаться, что речь идет всего лишь о терминологии, на самом деле имеется громадное концептуальное различие между полем и действием на расстоянии. Согласно полевой интерпретации электромагнетизма, заряд не оказывает мгновенного воздействия на другие области пространства. Нужно время на перестройку поля. Движущийся заряд создает в непосредственной близости от себя поле, которое проникает (хотя и очень быстро) во все области пространства. Тела узнают о движении удаленного заряда только после того, как свет (представляющий комбинацию электрических и магнитных полей) сумеет до них добраться. Таким образом, электрические и магнитные поля изменяются не быстрее, чем позволяет конечная скорость света. В каждой данной точке пространства поле настраивается только после того, как пройдет достаточное время, необходимое для того, чтобы влияние удаленного заряда достигло данной точки.
Однако, несмотря на огромную важность введенных Фарадеем понятий электромагнитных полей, они все же были больше эвристическими, чем математическими. Возможно, из-за обрывочного образования, математика не была любимым коньком Фарадея. Но другой английский физик, Джеймс Клерк Максвелл, включил идею Фарадея о поле в уравнения классической теории электромагнетизма. Максвелл был выдающимся ученым, в круг многочисленных интересов которого входили оптика и учение о цвете, математика овалов, термодинамика, кольца Сатурна, измерение широты с помощью чашки с патокой и вопрос о том, почему кошки приземляются на лапы, сохраняя угловой момент, хотя их бросают вверх тормашками[81].
Самым важным вкладом Максвелла в физику была система уравнений описывающих то, каким образом можно узнать значения электрического и магнитного полей, зная распределение зарядов и токов2. Из этих уравнений он вывел существование электромагнитных волн, т. е. волн всех видов электромагнитного излучения, существующих в вашем компьютере, телевизоре, микроволновой печи и во многих других удобных устройствах современного мира.
Однако Максвелл совершил одну ошибку. Как все другие физики его времени, он воспринял идею поля слишком материально. Он предполагал, что поле возникает благодаря колебаниям эфира, т. е. придерживался той идеи, которую, как мы увидим далее, окончательно развенчал Эйнштейн. Тем не менее Эйнштейн связывал имя Максвелла с происхождением специальной теории относительности: электромагнитная теория Максвелла позволила Эйнштейну понять идею о постоянстве скорости света, вызвавшую к жизни его монументальный труд.
Фотон
Классическая электромагнитная теория Максвелла привела к большому числу успешных предсказаний, но она была создана до квантовой механики и поэтому, очевидно, не включала квантовых эффектов. В наши дни физики изучают электромагнитное взаимодействие в рамках физики частиц. Основанная на ней теория электромагнетизма включает не только хорошо изученные и хорошо проверенные предсказания классической теории Максвелла, но и предсказания квантовой механики. Поэтому она является более полной и более точной теорией электромагнетизма, чем ее классическая предшественница. Действительно, квантовая теория электромагнетизма позволила получить невероятно точные предсказания, проверенные с неслыханной точностью в одну миллиардную долю[82].
Квантовая теория электромагнетизма объясняет электромагнитное взаимодействие обменом частицей по имени фотон — квантом света, который мы рассматривали в предыдущей главе. Происходит это следующим образом: начальный электрон испускает фотон, который подлетает к другому электрону, передает ему электромагнитное воздействие и затем исчезает. Благодаря такому обмену фотоны передают или переносят электромагнитную силу. Они производят такой же эффект, как конфиденциальные письма, которые передают информацию от одного адресата к другому, но после этого немедленно уничтожаются.
Мы знаем, что электрическая сила может иногда быть притягивающей, а иногда — отталкивающей: в случае притяжения взаимодействуют противоположно заряженные тела, в случае отталкивания заряды тел имеют одинаковый знак, положительный или отрицательный. Силу отталкивания, передаваемую фотоном, можно представить себе как взаимодействие между двумя конькобежцами, которые попеременно бросают друг другу шар для боулинга. Каждый раз, как один из конькобежцев ловит шар, он немного скользит по льду в сторону от своего партнера. С другой стороны, возникновение сил притяжения напоминает двух новичков, бросающих друг другу «фрисби» [83]; в противоположность конькобежцам, удаляющимся все дальше друг от друга, начинающие игроки в фрисби будут с каждым удачным броском приближаться друг к другу.
Фотон — это первый пример калибровочного бозона, фундаментальной элементарной частицы, ответственной за перенос конкретного взаимодействия. (Слово «калибровочный» звучит страшнее, чем оно есть на самом деле; физики начали использовать его в конце 1800-х годов, благодаря отдаленной аналогии с калибровкой железнодорожной колеи для определения расстояния между рельсами. Сто лет назад сам термин был намного известнее.) Другими примерами калибровочных бозонов являются слабые бозоны и глюоны. Эти частицы являются переносчиками слабых и сильных взаимодействий соответственно.
В период между концом 1920-х и 1940-ми годами английский физик Поль Дирак, американцы Ричард Фейнман и Юлиан Швингер, а также Син-Итиро Томонага, работавший независимо в послевоенной Японии, разработали квантово-механическую теорию фотона. Созданную ими область квантовой теории они назвали квантовой электродинамикой (КЭД). Эта область науки включает все предсказания классической теории электромагнетизма, а также вклад частиц (квантов) в физические процессы, т. е. взаимодействия, порождаемые обменом или рождением квантовых частиц.
КЭД предсказывает, как обмен фотоном порождает электромагнитное взаимодействие. Например, в процессе, изображенном на рис. 47, два электрона влетают в область взаимодействия, обмениваются фотоном, а затем возникают в конечном состоянии (например, с конечной скоростью и направлением движения) за счет влияния сообщенной им электромагнитной силы. Теория поля сопоставляет каждому элементу диаграммы определенные числа, так что саму диаграмму можно использовать для количественных предсказаний. Эта картинка является примером диаграммы Фейнмана, названной так в честь Ричарда Фейнмана, и представляет собой графический способ описания взаимодействий в квантовой теории поля. (Фейнман был так горд этой выдумкой, что нарисовал некоторые диаграммы на своем фургоне.)
Однако не все процессы КЭД включают фотоны, которые уничтожаются. Кроме эфемерных промежуточных или внутренних частиц[84], как те фотоны, что определяют электромагнитные взаимодействия и которые рождаются и почти сразу же уничтожаются, имеются и реальные внешние фотоны — частицы, входящие в область взаимодействия или покидающие ее. Иногда такие частицы отклоняются, иногда превращаются в другие частицы. В любом случае, частицы, которые входят в область взаимодействия или покидают ее, являются реальными физическими частицами.
Квантовая теория поля
Квантовая теория поля — инструмент, с помощью которого мы изучаем частицы[85], — основана на вечных и вездесущих объектах, которые способны порождать и уничтожать эти частицы. Такими объектами являются «поля» квантовой теории поля. Подобно классическим электромагнитным полям, квантовые поля — это объекты, заполняющие пространство-время. Но квантовые поля играют и другую роль. Они порождают или поглощают элементарные частицы. Согласно квантовой теории поля, частицы могут рождаться или уничтожаться где угодно и в любое время.
Например, электрон или фотон могут возникать или исчезать где угодно в пространстве. Квантовые процессы разрешают числу заряженных частиц во Вселенной изменяться за счет рождения и уничтожения частиц. Каждая частица рождается или уничтожается своим собственным полем. В квантовой теории поля не только электромагнетизм, но все силы и взаимодействия описываются с помощью полей, которые могут создавать новые или уничтожать уже существующие частицы.
Согласно квантовой теории частицы можно рассматривать как возбуждения квантового поля. В то время как вакуум, состояние без частиц, содержит только постоянные поля, состояния с частицами содержат поля с выпуклостями и изгибами, соответствующими частице. Когда в поле появляется выпуклость, рождается частица, когда поле поглощает эту выпуклость, чтобы вновь стать постоянным, частица уничтожается.
Поля, порождающие электроны и фотоны, должны существовать везде, чтобы гарантировать, что все взаимодействия могут происходить в любой точке пространства-времени. Это существенный момент, так как взаимодействия локальны, что означает, что во взаимодействии могут участвовать только частицы, находящиеся в одном месте. Действие на расстоянии скорее напоминает волшебство. Но частицы не обладают экстрасенсорным восприятием — чтобы взаимодействовать, им нужно быть в непосредственном контакте.
Электромагнитные взаимодействия могут происходить и между удаленными зарядами, не находящимися в прямом контакте, однако только благодаря содействию фотона или некоторых других частиц, имеющих непосредственный контакт с обеими взаимодействующими заряженными частицами. В этом случае кажется, что заряды действуют друг на друга мгновенно, но такое впечатление создается только потому, что скорость света столь велика. На самом деле взаимодействие происходит за счет локальных процессов; фотон совмещается сначала с одной из заряженных частиц, а затем с другой. Поэтому поле должно родить и уничтожить фотон точно в тех местах, где находятся заряженные частицы.
Античастицы и позитрон
Квантовая теория поля указывает также, что у каждой частицы должен существовать двойник, известный как античастица. Том Стоппард в пьесе «Хэпгуд» говорит об античастицах: «Когда частица встречается с античастицей, они уничтожают друг друга, они превращаются во взрыв энергии, понимаешь?» Любой любитель научной фантастики знает об античастицах. Из них сделано оружие для уничтожения Вселенной, они являются топливом для кораблей в сериале «Звездный путь. Военный корабль „Энтерпрайз“»[86]
Хотя эти приложения выдуманы, сами античастицы вполне реальны. Они действительно входят составной частью в картину физики частиц. В теории поля и Стандартной модели античастицы так же существенны, как и частицы. На самом деле античастицы — это те же частицы, за исключением того, что все их заряды имеют противоположные знаки.
Античастицы впервые ввел Поль Дирак, развивая квантовую теорию поля, описывающую электрон. Он нашел, что квантовая теория, совместная как с квантовой механикой, так и со специальной теорией относительности, с необходимостью включает античастицы. Он не вводил их в теорию сознательно. Когда Дирак учел специальную теорию относительности, получившаяся теория сама выплюнула античастицы. Их существование есть необходимое следствие релятивистской квантовой теории поля.
Приведем грубое доказательство того, почему наличие античастиц является следствием специальной теории относительности. Заряженные частицы могут двигаться в пространстве вперед и назад. Согласно специальной теории относительности, такие частицы должны быть способны с таким же успехом путешествовать вперед и назад по времени. Однако, насколько мы знаем, ни частицы, ни что-либо еще, в существовании чего мы уверены, не могут на самом деле путешествовать назад по времени. Вместо этого движущиеся назад по времени частицы заменяются противоположно заряженными античастицами. Античастицы воспроизводят эффекты, которые случились бы с путешествующими назад по времени частицами, так что даже без последних предсказания квантовой теории поля совместимы со специальной теорией относительности.
Представим себе кинофильм, в котором заснят ток отрицательно заряженных электронов, распространяющихся из одной точки в другую. Затем вообразим, что кинофильм прокручивается назад. Отрицательный заряд в этом случае будет двигаться назад, или, эквивалентно (до тех пор, пока рассматривается заряд), положительный заряд будет двигаться вперед. Этот положительно заряженный распространяющийся вперед ток создается током позитронов, положительно заряженных античастиц электронов, который поэтому действует как обращенный во времени ток электронов.
Квантовая теория поля утверждает, что если существует некая заряженная частица, например, электрон, то должна существовать соответствующая античастица с противоположным зарядом. Например, так как электрон обладает зарядом -1, позитрон обладает зарядом +1. Античастица похожа на частицу во всех отношениях, кроме заряда. Заряд протона также равен +1, но сам протон в 2000 раз тяжелее электрона, и поэтому он не может быть его античастицей.
Как правильно говорит Стоппард, когда античастицы входят во взаимодействие с частицами, они действительно аннигилируют. Так как сумма зарядов частицы и ее античастицы всегда равна нулю, то они могут аннигилировать и взаимно уничтожиться. Суммарный заряд частицы и античастицы равен нулю, и из соотношения Эйнштейна E = mc2 следует, что вся масса может превратиться в энергию.
С другой стороны, энергия может превратиться в пару частица — античастица, если количество энергии достаточно для такого превращения. Как аннигиляция, так и рождение частиц происходят в ускорителях частиц больших энергий, на которых физики проводят эксперименты по изучению тяжелых частиц, масса которых слишком велика, чтобы обнаруживаться в обычном веществе. В таких коллайдерах частица и античастица сталкиваются друг с другом и аннигилируют, создавая вспышку энергии, из которой возникают новые пары частиц и античастиц.
Так как вещество, в частности атомы, состоит из частиц, а не античастиц, то можно утверждать, что такие античастицы, как позитрон, в природе не встречаются. Однако они могут быть созданы на короткое время на коллайдерах, в горячих областях Вселенной, и даже в больницах, где для выявления признаков рака используются позитронные эмиссионные томографы.
Джерри Габриэлзе, мой коллега по физическому факультету Гарварда, непрерывно занимается производством античастиц в подвале здания Джефферсоновской лаборатории, где я работаю. Благодаря исследованиям Джерри и других физиков, мы с высокой степенью точности знаем, что античастицы действительно идеально похожи на своих двойников частиц по массе и гравитационному притяжению, но имеют противоположный заряд. Однако количество этих античастиц очень мало и не может причинить никакого беспокойства. Могу заверить любителей научной фантастики, что эти античастицы причиняют зданию намного меньше повреждений, чем постоянные работы по строительству новых лабораторий и офисов, всегда сопровождающиеся большим количеством видимых и слышимых разрушений.
Электроны, позитроны и фотоны — это простейшие и наиболее доступные частицы. Не случайно электрические силы и электроны были первыми ингредиентами Стандартной модели, которые сумели понять физики. Однако электрон, позитрон и фотон не исчерпывают список известных частиц, а электромагнетизм — не единственное известное взаимодействие.
На рис. 32 и 33 (стр. 77) я привела список известных частиц и негравитационных взаимодействий[87]. Я изъяла из списка гравитационное взаимодействие, так как оно качественно отличается от других взаимодействий и должно рассматриваться отдельно. Несмотря на прозаические имена двух из этих взаимодействий — слабое и сильное, они обладают множеством интересных свойств. В следующих двух разделах мы увидим, что это за свойства.
Слабое взаимодействие и нейтрино
Несмотря на то что в повседневной жизни вы не замечаете слабого взаимодействия, потому что оно действительно слабо, это взаимодействие существенно для многих ядерных процессов. Слабое взаимодействие объясняет некоторые типы распада ядер, например, распад ядра калия-40 (К40) (обнаружен на Земле, распад достаточно медленный, в среднем один миллиард лет[88], так что за счет этого распада продолжает разогреваться сердцевина Земли), и, конечно, распад самого нейтрона. Благодаря ядерным процессам меняется структура ядер и число нейтронов в них, что приводит к высвобождению большого количества энергии. Эту энергию можно использовать в ядерных электростанциях или ядерных бомбах, а также в других целях.
Например, слабое взаимодействие играет важную роль в создании тяжелых элементов, образующихся во время катастрофических взрывов сверхновых. Слабое взаимодействие существенно также для свечения звезд, в том числе Солнца. Оно запускает цепочку реакций, в которых водород превращается в гелий. Приводимые в действие слабым взаимодействием ядерные процессы приводят к непрерывному изменению состава Вселенной. Из наших знаний ядерной физики можно вывести, что примерно 10 % первичного водорода во Вселенной было использовано в качестве ядерного топлива в звездах. (К счастью, оставшиеся 90 % водорода гарантируют, что Вселенной не придется в ближайшее время зависеть от посторонних источников энергии.)
Несмотря на важность слабого взаимодействия, ученые лишь сравнительно недавно определили его свойства. В 1862 году Уильям Томсон (позднее лорд Кельвин[89]), один из самых уважаемых физиков того времени, чрезвычайно недооценил возраст Солнца и Земли, так как он не знал о ядерных процессах, происходящих за счет слабого взаимодействия (которое, надо отдать ему должное, не было еще тогда открыто). У. Томсон основывал свою оценку на единственном известном источнике светимости — нагреве. Он вывел, что доступная за счет этого энергия способна поддерживать свечение Солнца не более 30 миллионов лет.
Этот результат не понравился Чарльзу Дарвину. Он получил намного более близкий к правильному минимальный возраст Земли, оценив промежуток времени, требуемый для эрозии и вымывания долины Вельда на юге Англии. Дарвиновская оценка в 300 миллионов лет была тем более привлекательной, что она оставляла достаточно времени для естественного отбора, который мог бы обеспечить большое разнообразие найденных на Земле видов.
Однако все, включая самого Дарвина, сочли, что Томсон, физик блистательной репутации, был прав. Дарвин был настолько убежден в правильности вычислений Томсона и в его репутации, что изъял собственные оценки времени из последующих изданий своей книги Происхождение видов. Только после того, как Резерфорд открыл важную роль радиации[90], дарвиновская идея о большем возрасте Земли было реабилитирована, и теперь установлено, что возраст Земли и Солнца равен 4,5 миллиарда лет, что намного больше оценок Томсона и Дарвина.
В 1960 годах американские физики Шелдон Глэшоу и Стивен Вайнберг, а также пакистанский физик Абдус Салам, работая независимо друг от друга (и не всегда согласованно), разработали электрослабую теорию, которая объясняет слабые взаимодействия и проливает свет на происхождение электромагнетизма[91]. Согласно электрослабой теории, эффекты слабого взаимодействия порождаются обменом частицами, называемыми слабыми калибровочными бозонами, по аналогии с тем, как электромагнитное взаимодействие обусловлено обменом фотонами. Имеются три слабых калибровочных бозона. Два из них, W+ и W-, обладают электрическим зарядом (W происходит от слова weak, т. е. слабый, а знаки «+» или «-» указывают на знак электрического заряда калибровочного бозона). Третий бозон Z нейтрален (название происходит от слова zero, т. е. ноль).
Как и в случае обмена фотонами, обмен слабыми калибровочными бозонами порождает силы, которые могут быть силами притяжения или отталкивания, в зависимости от слабых зарядов частиц. Слабые заряды — это числа, играющие ту же роль для слабого взаимодействия, которую играет электрический заряд для электромагнитного взаимодействия. Слабое взаимодействие испытывают только частицы, обладающие слабым зарядом, причем их конкретный заряд определяет интенсивность и тип испытываемого ими взаимодействия.
Однако есть несколько важных различий между электромагнитным и слабым взаимодействиями. Одно из самых удивительных — это то, что слабое взаимодействие отличает левое от правого, или, как сказали бы физики, нарушает четность. Нарушение четности означает, что зеркальные образы частиц ведут себя различно по отношению друг к другу. Китайско-американские физики Ч. Н. Янг и Т. Д. Ли в 1950-х годах сформулировали теорию нарушения четности, а другой китайско-американский физик Ц. С. Ву подтвердила ее экспериментально в 1957 году. В том же году Янг и Ли получили Нобелевскую премию по физике. Любопытно, что Ву, единственная женщина, сыгравшая роль в развитии обсуждаемой нами Стандартной модели, не получила Нобелевской премии за свое важное открытие.
Некоторые нарушения зеркальной симметрии должны быть знакомы читателю. Например, ваше сердце находится в левой стороне тела. Но если бы эволюция протекала иначе и люди в конце концов имели бы сердце справа, можно было бы ожидать, что все его свойства были бы такими же, как мы наблюдаем сейчас. Тот факт, что сердце находится с одной стороны, а не с другой, никак не влияет на любые фундаментальные биологические процессы.
В течение многих лет вплоть до эксперимента Ву в 1957 году считалось «очевидным», что физические законы (хотя не обязательно физические тела) не могут предпочитать правое левому или наоборот. Действительно, а почему они должны предпочитать одно другому? Совершенно определенно известно, что тяготение и электромагнетизм, как и многие другие взаимодействия, не отличают левое от правого. Тем не менее слабое взаимодействие, являющееся фундаментальным взаимодействием в природе, отличает левое от правого. Как это ни удивительно, слабое взаимодействие нарушает зеркальную симметрию.
Как может взаимодействие предпочитать правое левому или наоборот? Ответ связан с понятием внутреннего спина фермионов. По аналогии с тем, что конструкция винта предусматривает, что при завинчивании он вращается по часовой стрелке, а не против часовой стрелки, так и у частиц может быть встроенная правая или левая спиральность, указывающая направление их вращения (по отношению к направлению их импульса) (рис. 48). Многие частицы, например электрон и протон, могут вращаться в одном из двух направлений — либо налево, либо направо. Слово киральность, происходящее от греческого слова χειρ, т. е. рука, относится к двум возможным направлениям вращения. Частицы могут быть левокиральными или правокиральными, как пальцы на ваших руках, которые на одной руке расположены справа налево, а на другой слева направо[92].

Слабое взаимодействие нарушает зеркальную симметрию, действуя по-разному на левокиральные и правокиральные частицы, которые в физике принято называть просто левыми и правыми. Оказывается, что только левые частицы участвуют в слабых взаимодействиях. Например, левый электрон будет испытывать слабое взаимодействие, а электрон, вращающийся направо, — не будет. Эксперименты ясно показывают, что мир устроен именно так, но нет интуитивного механического объяснения, почему так должно быть.
Вообразите силу, которая может действовать только на вашу левую руку, но не на правую! Я только и могу сказать, что нарушение четности — поразительное, но хорошо установленное свойство слабых взаимодействий. Это одно из самых интригующих свойств Стандартной модели. Например, электроны, испускающиеся при распадах нейтронов, всегда левые. Слабые взаимодействия нарушают зеркальную симметрию, так что когда я перечисляю полный список элементарных частиц и возможных для них взаимодействий (рис. 52 на стр. 145), я должна отдельно указывать левые и правые частицы.
Нарушение четности, само по себе странное, является не единственным новым свойством слабых взаимодействий. Второе, в равной степени важное свойство заключается в том, что слабое взаимодействие может реально превращать частицу одного типа в частицу другого типа (сохраняя, тем не менее, полный электрический заряд). Например, когда нейтрон взаимодействует со слабым калибровочным бозоном, может возникнуть протон (рис. 49). Это сильно отличается от взаимодействия фотона, который никогда не сможет изменить полное число заряженных частиц любого конкретного типа (т. е. число частиц минус число античастиц), например, число электронов минус число позитронов. (Для сравнения, на рис. 50 показан фотон, взаимодействующий с электроном, который входит в область взаимодействия и покидает ее, а также схематическая диаграмма того типа, что мы использовали ранее.) Именно взаимодействие заряженного калибровочного бозона с нейтроном и протоном позволяет изолированному нейтрону распадаться, превращаясь в совершенно другие частицы.

Однако, поскольку нейтрон и протон имеют разные массы и несут разные заряды, нейтрон должен при распаде породить протон и другие частицы так, чтобы при этом сохранялись заряд, энергия и импульс. Оказывается, что при распаде нейтрона образуется не только протон, но также рождаются электрон и частица, называемая нейтрино[93]. Такой процесс, показанный на рис. 51, называется бета-распадом.
Когда бета-распад был впервые зарегистрирован, никто ничего не знал о нейтрино, которое участвует только в слабых взаимодействиях, но не в электромагнитных. В то же время детекторы частиц могут обнаружить только заряженные частицы или те частицы, которые выделяют энергию. Так как нейтрино не имеет электрического заряда и не распадается, оно остается невидимым для детекторов, так что никто не знал о его существовании.
Однако без нейтрино бета-распад выглядел так, как будто в нем не сохранялась энергия. Закон сохранения энергии является фундаментальным принципом всей физики. Он утверждает, что энергия не может ни возникать, ни уничтожаться, а может только переноситься из одного места в другое. Предположение о том, что в бета-распаде не сохраняется энергия, было возмутительным, однако многие уважаемые физики[94], не имевшие представления о существовании нейтрино, были готовы согласиться с таким радикальным (и ошибочным) утверждением.
В 1930 году Вольфганг Паули предложил путь к научному спасению скептиков, который он сам назвал «отчаянной попыткой» — он предположил существование новой электрически нейтральной частицы[95]. Идея Паули состояла в том, что нейтрино тайком крадет часть энергии, выделяющейся при распаде нейтрона. Тремя годами спустя Энрико Ферми дал солидное теоретическое обоснование существования «маленькой» нейтральной частицы, которую он назвал нейтрино[96]. Тем не менее гипотеза о существовании нейтрино представлялась в те времена настолько сомнительным выходом из положения, что ведущий научный журнал Nature отклонил статью Ферми, так как «она содержала размышления, слишком далекие от интересов читателя».
Однако идеи Паули и Ферми были правильными, и в наши дни физики полностью согласны с существованием нейтрино[97]. На самом деле, мы знаем сейчас, что нас непрерывно пронизывают потоки нейтрино, рождающихся вместе с фотонами в ядерных реакциях на Солнце. Ежесекундно сквозь нас проходят триллионы солнечных нейтрино, но их взаимодействия столь слабы, что мы этого никогда не замечаем. Те нейтрино, в существовании которых мы твердо уверены, являются левыми; правые нейтрино либо не существуют, либо очень тяжелы, слишком тяжелы для того, чтобы рождаться, либо взаимодействуют очень слабо. Какая бы из гипотез ни оказалась правильной, правые нейтрино никогда не рождались на ускорителях, и мы их никогда не видели. Поскольку мы значительно более уверены в существовании левых, а не правых нейтрино, я показала на рис. 52, где приведены отдельно левые и правые частицы, только левые нейтрино.
Итак, мы знаем теперь, что слабые взаимодействия действуют только на левые частицы и могут менять тип частиц. Однако, чтобы по-настоящему понять слабые взаимодействия, нам нужна теория, предсказывающая взаимодействия слабых калибровочных бозонов, являющихся переносчиками слабых сил. Физики сразу же поняли, что построить такую теорию не так-то легко. Им потребовалось совершить ряд важных теоретических открытий, прежде чем действительно понять слабое взаимодействие и его следствия.
В конечном итоге проблема состояла в странном свойстве слабого взаимодействия — оно резко спадало на очень малом расстоянии 10-18 м. В этом оно полностью отличается от гравитации или электромагнетизма, для которых, как мы видели в гл. 2, напряженность поля уменьшается с расстоянием обратно пропорционально квадрату расстояния. Хотя при увеличении расстояния гравитация и электромагнетизм становятся все слабее, их интенсивность не спадает так же быстро, как слабое взаимодействие. Фотон переносит электромагнитное взаимодействие на большие расстояния. Почему слабое взаимодействие ведет себя совершенно иначе?

Было очевидно, что для объяснения ядерных процессов типа бета-распада физики должны найти новый тип взаимодействия, но было неясно, каким может быть это взаимодействие. До того, как Глэшоу, Вайнберг и Салам построили свою теорию слабого взаимодействия, Ферми попытался предложить теорию, включавшую новые типы взаимодействия четырех частиц, например, протона, нейтрона, электрона и нейтрино. Это взаимодействие Ферми непосредственно порождало бета-распад без обращения к промежуточному слабому калибровочному бозону. Иными словами, взаимодействие позволяло нейтрону непосредственно превращаться в свои продукты распада — протон, электрон и нейтрино.
Однако даже в то время было ясно, что теория Ферми не может быть правильной теорией, применимой при всех энергиях. Хотя при низких энергиях ее предсказания были правильными, при высоких энергиях они становились полностью неверными, приводя к слишком сильным взаимодействиям. Если предположить (что неверно), что теория Ферми применима к частицам большой энергии, то мы придем к бессмысленным предсказаниям вроде того, что частицы должны взаимодействовать с вероятностью больше единицы. Это невозможно, так как ничто не может случаться чаще, чем всегда.
Хотя теория, основанная на взаимодействии Ферми, была прекрасной эффективной теорией для объяснения взаимодействий при низких энергиях и между достаточно удаленными частицами, физики видели, что им нужно более фундаментальное объяснение процессов типа бета-распада, если они хотят знать, что происходит при высоких энергиях. Казалось, что теория, основанная на передаче взаимодействий слабыми калибровочными бозонами, должна намного лучше работать при высоких энергиях, однако никто не знал, как учесть короткодействующий характер слабого взаимодействия.
Малый радиус оказался следствием ненулевых масс слабых калибровочных бозонов. В физике частиц связи, накладываемые соотношением неопределенностей и специальной теорией относительности, имеют заметные следствия. В конце гл. 6 я обсуждала вопрос о наименьших расстояниях, на которых частица данной энергии, например, характерной энергии слабого взаимодействия или планковской энергии, может быть подвержена действию сил. В силу соотношения специальной теории относительности между энергией и массой (E = mc2) массивным частицам, например слабым калибровочным бозонам, автоматически присущи аналогичные соотношения между массой и расстоянием.
В частности, взаимодействие, осуществляемое путем обмена частицей некоторой массы, становится тем слабее на больших расстояниях, чем меньше масса. (Это расстояние пропорционально также постоянной Планка и обратно пропорционально скорости света[98].) Приведенная в гл. 6 связь между массой и расстоянием говорит нам, что слабый калибровочный бозон, масса которого примерно равна 100 ГэВ, автоматически передает слабое взаимодействие только частицам, находящимся на расстоянии 10-18 м. На больших расстояниях переносимое частицей взаимодействие становится необычайно малым, слишком малым для того, чтобы мы могли это когда-нибудь обнаружить.
Ненулевая масса слабого калибровочного бозона представляется критической для успеха теории слабого взаимодействия. Масса есть причина того, что слабое взаимодействие действует только на очень коротких расстояниях, и настолько слабо, что кажется практически несуществующим на больших расстояниях. В этом отношении слабые калибровочные бозоны отличаются от фотона и гравитона, которые не имеют массы. Так как фотон и гравитон, частица, переносящая гравитационное взаимодействие, переносят энергию и импульс, но не имеют массы, они могут передавать взаимодействия на большие расстояния.
Понятие о безмассовой частице может показаться странным, но с точки зрения физики частиц в нем нет ничего удивительного. Безмассовость частиц говорит нам, что эти частицы распространяются со скоростью света (в конце концов, свет состоит из безмассовых фотонов), кроме того, энергия и импульс таких частиц всегда подчиняется определенному соотношению: энергия пропорциональна импульсу.
С другой стороны, переносчики слабого взаимодействия имеют массу. С точки зрения физики частиц, именно массивный (а не безмассовый) калибровочный бозон представляется странным. Ключевое открытие, проложившее дорогу теории слабого взаимодействия, состояло в понимании происхождения масс слабых калибровочных бозонов, благодаря которым зависимость слабого взаимодействия от расстояния так отличается от этой зависимости для электромагнитного взаимодействия. Механизм, который порождает массы слабых калибровочных бозонов, известный как механизм Хиггса, будет обсуждаться в гл. 10. Как мы увидим в гл. 12, лежащая в основе теория, т. е. точная модель, которая придает частицам их массы, является одной из величайших загадок, с которыми сталкиваются сейчас физики-частичники. Одной из привлекательных черт теории дополнительных измерений является то, что она способна помочь решить эту загадку.
Кварки и сильные взаимодействия
Мой приятель-физик однажды объяснял одной из моих сестер, что он изучает «сильное взаимодействие, которое называется сильным потому, что оно очень сильное». Хотя сестра не сочла это особенно убедительным, но на самом деле термин для сильного взаимодействия выбран удачно. Это действительно необычайно мощное взаимодействие. Оно настолько сильно связывает вместе составные части протона, что в обычных условиях они никогда не разъединяются. Сильное взаимодействие имеет только косвенное отношение к последующим частям этой книги, так что здесь для полноты я изложу лишь основные факты, касающиеся этого взаимодействия.
Сильное взаимодействие, которое описывается теорией, называемой квантовой хромодинамикой (КХД), является последним из взаимодействий Стандартной модели, которое мы можем объяснить с помощью обмена калибровочными бозонами. Это взаимодействие также было открыто только в прошлом веке. Сильные калибровочные бозоны называются иначе глюонами, так как они передают взаимодействие как некий клей[99], связывающий вместе сильно взаимодействующие частицы.
В 1950-е и 1960-е годы физики открыли одну за другой много частиц. Отдельным частицам были присвоены названия букв греческого алфавита, например, π (пион), θ (тета) и Δ (Дельта). Все вместе эти частицы были названы адронами от греч. слова αδρος («тяжелый»).
Действительно, все адроны были намного массивнее электрона. Большей частью они были сравнимы по массе с протоном, масса которого в 2000 раз больше массы электрона. Невероятное многообразие адронов было загадкой, пока физик Мюррей Гелл-Манн[100] не высказал в начале 1960-х годов гипотезу, что многие адроны не являются фундаментальными частицами, а сами состоят из частиц, которые он назвал кварками.
Слово «кварк» было взято Гелл-Манном из романа «Поминки по Финнегану» Джеймса Джойса: «Три кварка для мистера Марка! Ему уж точно немного достанется на барке. И все его богатство ему уж ни к чему»[101]. Насколько я могу понять, все это имеет очень малое отношение к физике кварков, не считая двух вещей: кварков три, и их трудно понять[102].
Гелл-Манн предположил, что существуют три разновидности кварков[103], которые называют сейчас верхний (u), нижний (d) и странный (s), и многочисленные адроны соответствуют многим возможным комбинациям связанных друг с другом кварков. Если его гипотеза верна, то все адроны должны закономерно разделяться на предсказуемые группы. Как часто случается, когда предлагаются новые физические принципы, Гелл-Манн на самом деле не верил в существование кварков. Тем не менее его предположение было довольно смелым, так как в это время были открыты только некоторые из предсказываемых адронов. Поэтому для Гелл-Манна стало большой победой открытие недостающих адронов и подтверждение гипотезы кварков, что проложило ему путь к получению Нобелевской премии по физике 1969 года.
Хотя физики согласились с тем, что адроны состоят из кварков, прошло целых девять лет после этой гипотезы, прежде чем адронная физика была объяснена в рамках сильного взаимодействия. Парадоксально, что последним объясненным взаимодействием было сильное взаимодействие, отчасти из-за его колоссальной интенсивности. Сейчас мы знаем, что сильное взаимодействие настолько велико, что фундаментальные частицы, например кварки, испытывающие сильное взаимодействие, всегда связаны друг с другом, так что их трудно изолировать и, следовательно, изучать. Частицы, испытывающие сильное взаимодействие, не могут скитаться в одиночку, без компании.
Каждая разновидность кварков имеет три типа. Физики шутливо пометили разные типы цветами, и иногда называют типы кварков красным, зеленым и голубым. Цветные кварки всегда обнаруживаются связанными вместе с другими кварками и антикварками в нейтральную по цвету (бесцветную) комбинацию. Это те комбинации, в которых «заряды» сильного взаимодействия кварков и антикварков компенсируют друг друга, аналогично тому, как разные цвета при смешивании дают белый свет[104]. Существуют два типа бесцветных комбинаций. Стабильные адронные конфигурации содержат либо объединенные друг с другом кварк и антикварк, либо три связанных вместе кварка (без антикварков). Например, в частицах, называемых пионами, кварк спаривается с антикварком, а в протоне и нейтроне связаны вместе три кварка.
В адронах «заряд» сильного взаимодействия между кварками сокращается, во многом аналогично тому, как заряд положительно заряженного протона сокращается с зарядом отрицательно заряженного электрона в атоме. Но в отличие от атома, который можно ионизовать без труда, очень трудно разбить на составные части такие объекты, как протон и нейтрон, которые необычайно сильно связаны глюонами — переносчиками сильного взаимодействия.
Теперь мы почти готовы вернуться к открытию кварков, метафорически описанному в ревизионистской сказке Афины. Протон и нейтрон состоят из комбинаций трех кварков, в которых взаимно сокращается заряд, связанный с сильным взаимодействием. Протон содержит два u-кварка и один d-кварк — разные типы кварков с разными электрическими зарядами. Так как электрический заряд u-кварка равен +2/з, а электрический заряд d-кварка равен -1/3, электрический заряд протона равен +1. А нейтрон содержит один u-кварк и два d-кварка, так что его электрический заряд равен 0 (сумма зарядов -1/3, -1/3 и +2/3).
Кварки можно представить как твердые точечноподобные объекты, находящиеся в большом рыхлом протоне. Они внедрены в протон или нейтрон, как горошины, запрятанные под матрасами. Но как и в случае с прыгающей принцессой, ставящей себе синяки при ударе о горошину, энергичный экспериментатор может выстрелить по протону электроном большой энергии, который испускает фотон, рикошетом отскакивающий от кварка. Это совсем не похоже на фотон, отскакивающий от большого мягкого тела, точно так же, как альфа-частица в опыте Резерфорда, отскакивающая от жесткого ядра, сильно отличается от альфа-частицы, отскакивающей от размазанного положительного заряда.
Эксперимент по глубоко-неупругому рассеянию, выполненный Фридманом, Кендаллом и Тейлором в Станфордском центре линейного ускорителя (SLAC), продемонстрировал существование кварков, зарегистрировав указанный эффект. Экспериментаторы показали, каким образом ведут себя электроны, рассеивающиеся на протонах, тем самым продемонстрировав первое экспериментальное свидетельство реального существования кварков. За это открытие Джерри Фридман и Генри Кендалл (они были моими коллегами в Массачусетском технологическом институте), а также Ричард Тейлор получили Нобелевскую премию по физике 1990 года.
Когда кварки рождаются в столкновениях частиц высоких энергий, они еще не связаны в адроны, но это не означает, что они изолированы. У них всегда есть сопровождающая их свита из других кварков и глюонов, обеспечивающая нейтральность всей комбинации по отношению к сильному взаимодействию. Кварки никогда не возникают как свободные объекты без сопровождения, а всегда экранированы многими другими сильно взаимодействующими частицами. Вместо отдельного изолированного кварка экспериментатор регистрирует множество частиц, состоящих из кварков и глюонов и летящих примерно в одном направлении.
В целом группы частиц, состоящие из кварков и глюонов и согласованно двигающиеся в определенном направлении, носят название струй. Как только образуется струя частиц большой энергии, она напоминает канат, в том смысле, что она никогда не исчезает. При разрезании каната вы получаете два новых куска каната. Аналогично, когда струи разделяются за счет взаимодействий, их отдельные куски могут образовать новые струи, но никогда не удастся разделить их на отдельные, изолированные кварки и глюоны. Стефен Сондхайм скорее всего не думал об ускорителях частиц высоких энергий, когда писал стихи для песни «Ракет»[105] в «Вестсайдской истории», но его слова прекрасно подходят к струям сильно взаимодействующих частиц. Энергичные сильно взаимодействующие частицы всегда держатся вместе. «Они никогда не одиноки… Они — под защитой».
Известные фундаментальные частицы
В этой главе уже было рассказано о трех из четырех известных взаимодействий — электромагнитном, слабом и сильном. Остающееся гравитационное взаимодействие настолько слабо, что оно никак не влияет на экспериментально наблюдаемые предсказания физики частиц.
Но мы еще не закончили представление всех частиц Стандартной модели. Эти частицы идентифицируются по своим зарядам, а также по своей киральности. Как я рассказывала ранее, левые и правые частицы могут иметь (и на самом деле имеют) различные слабые заряды.
Специалисты разделяют все эти частицы на кварки и лептоны. Кварки — это фундаментальные фермионы, способные участвовать в сильных взаимодействиях. Лептоны — это фермионы, не способные участвовать в сильных взаимодействиях. Примерами фермионов могут служить электроны и нейтрино. Слово «лептон» происходит от греческого слова λεπτος, означающего «маленький» или «легкий», что указывает на малую массу электрона.
Странно, что в дополнение к частицам, существенным для структуры атома, таким как электрон и и- и d-кварки, существуют дополнительные частицы, которые хотя и больше по массе, но имеют те же заряды, что и уже упомянутые частицы. У всех легчайших стабильных кварков и лептонов есть более тяжелые копии. Никто не знает, почему они существуют и для чего они нужны.
Когда физики впервые поняли, что мюон, частица, впервые обнаруженная в космическом излучении, есть не что иное, как более тяжелая версия электрона (тяжелее в 200 раз), физик И. Раби спросил: «А кто его заказал?» Хотя мюон, как и электрон, отрицательно заряжен, он тяжелее электрона, и может в него распадаться. Иными словами, мюон нестабилен (см. рис. 53) и быстро превращается в электрон (и два нейтрино). Насколько мы сейчас знаем, мюон не играет никакой роли в строении вещества здесь, на Земле. Почему же он существует? Это одна из загадок Стандартной модели, которая, как мы надеемся, будет решена при дальнейшем развитии науки.
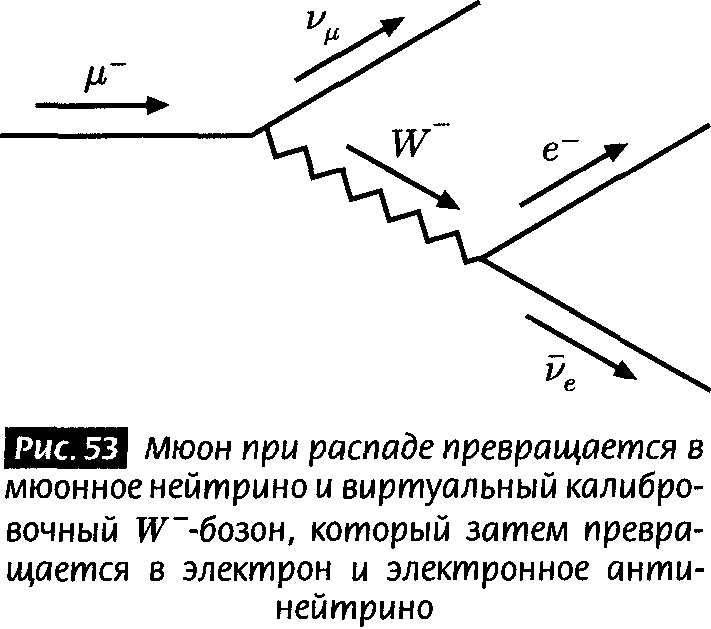
На самом деле существуют три копии полного набора частиц с одинаковыми зарядами Стандартной модели (рис. 52). Каждая из этих копий носит название поколения или, иногда, семейства. Первое поколение частиц содержит левый и правый электрон, левый и правый u-кварк, левый и правый d-кварк и левое нейтрино. Первое поколение содержит весь стабильный материал, из которого состоят атомы, а следовательно, и все стабильное вещество.
Второе и третье поколения включают нестабильные частицы, которые отсутствуют в «нормальном» известном веществе. Эти частицы не являются точными копиями первого поколения; их заряды тождественны зарядам частиц первого поколения, но сами частицы тяжелее. Они были обнаружены только после того, как были рождены на ускорителях частиц высоких энергий, но смысл их существования остается туманным. Второе поколение включает левый и правый мюон, левый и правый с-кварк и левый и правый s-кварк, а также стабильное левое мюонное нейтрино[106]. Третье поколение включает левый и правый тау-лептон, левый и правый t-кварк (называемый также топ-кварком), левый и правый b-кварк, а также левое тау-нейтрино. Тождественные копии конкретной частицы с определенным зарядом, каждая из которых является членом своего поколения, часто называют ароматами частицы этого типа.
Из рис. 52 можно видеть, что хотя в те времена, когда Гелл-Манн впервые высказал гипотезу о существовании кварков, было известно о существовании только трех ароматов кварков, сейчас мы знаем шесть ароматов: три типа u и три типа d, по одному в каждом поколении. В дополнение к самому u-кварку существуют еще два одинаково заряженных кварка типа и — кварки с и t. Аналогично, d-, s- и b-кварки являются разными ароматами кварка типа d. А мюон и тау-лептон есть более тяжелые ароматы электрона.
Физики все еще пытаются понять причину существования трех поколений и то, почему частицы имеют определенные массы. Это главные вопросы, касающиеся Стандартной модели, которые питают проводимые сейчас исследования. Вместе с коллегами я много работала над этими вопросами, но мы все еще ищем ответы.
Тяжелые ароматы существенно тяжелее легких. Хотя следующий тяжелый b-кварк был открыт в 1977 году, последний самый тяжелый t-кварк ускользал от экспериментаторов до 1995 года. Предметом следующей главы будут два эксперимента по физике частиц, в том числе тот, в котором был открыт t-кварк.
Что стоит запомнить
• Стандартная модель описывает негравитационные взаимодействия и частицы, испытывающие эти взаимодействия. В дополнение к хорошо известному электромагнитному взаимодействию, существуют два взаимодействия, действующих в рамках ядра — сильное взаимодействие и слабое взаимодействие.
• Слабое взаимодействие остается загадкой в Стандартной модели. В то время как два других взаимодействия переносятся безмассовыми частицами, калибровочный бозон, переносящий слабое взаимодействие, имеет массу.
• В дополнение к частицам, переносящим взаимодействия, Стандартная модель содержит частицы, испытывающие эти взаимодействия. Эти частицы разделены на две категории: кварки, испытывающие сильное взаимодействие, и лептоны, не испытывающие этого взаимодействия.
• Содержащиеся в веществе легкие кварки и лептоны (u-кварк, d-кварк и электрон) — не единственные известные частицы. Существуют и более тяжелые кварки и лептоны: для u-кварка, d-кварка и электрона имеется по две более тяжелых модификации.
• Тяжелые частицы нестабильны, т. е. они распадаются на более легкие кварки и лептоны. Однако они были созданы в экспериментах на ускорителях частиц, и было показано, что более тяжелые частицы участвуют в тех же взаимодействиях, что и обычные легкие, стабильные частицы.
• Каждая группа частиц, состоящая из заряженного лептона, кварка u-типа и кварка d-типа, называется поколением. Существуют три поколения, каждое из которых содержит, соответственно, все более тяжелые модификации частиц каждого типа. Такие разновидности частиц носят название ароматов. Существуют три кварковых аромата u-типа, три кварковых аромата d-типа, три аромата заряженного лептона и три аромата нейтрино.
• Далее я не буду использовать названия и детальное описание каждого конкретного кварка. Однако следует иметь представление о поколениях и ароматах из-за налагаемых этими понятиями сильных ограничений на свойства частиц, которые дают нам важнейшие ключи и ограничения на физику за рамками Стандартной модели.
• Важнейшим среди этих ограничений является то, что различные ароматы кварков и лептонов с одинаковыми зарядами не превращаются друг в друга. Теории, в которых частицы могут легко менять свой аромат, исключены. Далее мы увидим, что это является большим вызовом моделям нарушенной суперсимметрии и другим предлагавшимся расширениям Стандартной модели.
Глава 8
Экспериментальная интерлюдия: проверка Стандартной модели
One way, or another
I’m gonna find you…
Blondie[107]
Икару опять приснилось, что он встретил квантового детектива, на этот раз сыщик знал, что ему нужно, и у него была неплохая идея, где это должно быть. Все, что он должен был делать, — это ждать. Если он не ошибся, то рано или поздно его жертва появится.
Искать тяжелые частицы непросто. Но именно этим делом мы и должны заниматься, если собираемся выяснить лежащую в основе Стандартной модели структуру и в конце концов физический состав Вселенной. Наибольшая часть наших знаний о физике частиц получена с помощью экспериментов на ускорителях частиц высоких энергий, в которых сначала ускоряется быстро летящий пучок частиц, которые затем испытывают соударения с частицами других типов.
В коллайдерах частиц высоких энергий ускоренный пучок частиц на самом деле сталкивается с ускоренным пучком античастиц, так что они встречаются в малой области, содержащей огромное количество энергии. Эта энергия иногда превращается в тяжелые частицы, обычно не встречающиеся в природе. Коллайдеры частиц высоких энергий — то единственное место, где рождаются самые тяжелые известные частицы с момента Большого взрыва, когда значительно более горячая Вселенная содержала все частицы в изобилии. На коллайдерах в принципе можно создавать пары частиц и античастиц любого сорта, если только хватает энергии для рождения конкретной пары, что определяется формулой Эйнштейна E = mc2.
Однако целью физики высоких энергий является не только поиск новых частиц. Эксперименты на коллайдерах высоких энергий дают информацию о фундаментальных законах природы, которые не доступны для наблюдения никаким иным способом, законах, которые действуют в области, слишком малой для того, чтобы ее можно было увидеть непосредственно. Эксперименты при высоких энергиях — единственный способ исследования любых взаимодействий, действующих на необычайно малых расстояниях.
В этой главе пойдет речь о двух экспериментах на коллайдерах, которые, с одной стороны, очень важны для подтверждения предсказаний Стандартной модели, а с другой стороны, накладывают ограничения на то, какие возможные теории за этим стоят. Сами эксперименты производят большое впечатление.
Но они должны также дать вам почувствовать, с чем в будущем предстоит столкнуться физикам, когда они обратятся к поискам новых явлений, например дополнительных измерений.
Открытые топ-кварка
История поиска топ-кварка замечательно иллюстрирует трудности поиска частиц на коллайдере в ситуации, когда его энергии едва хватает для их рождения, и экспериментаторам приходится применять все свое мастерство. Хотя топ-кварк не является частью какого либо атома или известного вещества, без него Стандартная модель была бы несамосогласованной, так что большинство физиков с начала 1970-х годов было уверено в его существовании. Однако вплоть до 1995 года никому не удавалось зарегистрировать хотя бы один топ-кварк.
К этому времени эксперименты по поиску топ-кварка тщетно проводились много лет. Кварк b, следующая по массе частица Стандартной модели, масса которой в пять раз больше массы протона, был открыт в 1977 году. Хотя физики в то время полагали, что топ-кварк вот-вот будет открыт, и экспериментаторы уже вступили в соревнование, кто быстрее его найдет и прославится, ко всеобщему удивлению опыт за опытом не давал результатов. Топ-кварк не могли найти на коллайдерах, работавших при энергиях в 40, 60 и даже 100 раз больших, чем та, которая нужна для рождения протона. Очевидно, что топ-кварк был тяжелым, существенно тяжелее всех других кварков, которые были уже открыты. Когда наконец после 20 лет поисков топ-кварк проявился на опыте, оказалось, что его масса почти в 200 раз больше массы протона.
Поскольку топ-кварк так тяжел, соотношения специальной теории относительности утверждают, что он может родиться только на коллайдерах, работающих на сверхвысоких энергиях. Такие энергии неизбежно требуют больших размеров ускорителя, так что сконструировать и построить подобный ускоритель технически очень трудно.
Тем ускорителем, на котором в конце концов получили топ-кварк, стал Тэватрон в Батавии, штат Иллинойс, в 30 милях от Чикаго. Коллайдер в Фермилабе был изначально спроектирован на энергии, много меньшие тех, которые нужны для рождения топ-кварка, однако инженеры и физики внесли множество изменений, необычайно усиливших возможности коллайдера. В 1995 году в итоге всех этих улучшений Тэватрон приступил к работе при значительно большей энергии, чем запланированная, производя при этом намного больше соударений, чем могла исходная машина.
Тэватрон, который все еще работает, находится в Фермилабе, ускорительном центре, который был официально открыт в 1972 году и получил свое имя в честь физика Энрико Ферми. Когда я впервые посетила Фермилаб, меня очень позабавило, что в этом месте росла дикая пшеница, бродили гуси и, как ни странно, бизоны. Если не считать бизонов, местность была унылой и ничем не примечательной. Кинофильм Мир Вейна снимался в местечке Аврора в пяти милях к югу от Фермилаба, и если вы видели этот фильм, то можете легко представить себе окружающую Фермилаб местность. К счастью, тамошние физики достаточно привлекательны, чтобы несмотря ни на что можно было чувствовать себя счастливой.
Тэватрон получил свое имя потому, что он ускоряет как протоны, так и антипротоны до энергии в один ТэВ, т. е. 1000 ГэВ, — самой большой энергии, достигнутой до сих пор на ускорителе. Пучки протонов и антипротонов большой энергии, порождаемые Тэватроном, крутятся по кольцу и каждые 3–5 мкс сталкиваются друг с другом в двух точках соударения.
Две разные коллаборации экспериментаторов установили свои детекторы в каждой из двух точек соударения, где пересекаются пути пучков частиц и античастиц и могут происходить интересные физические явления. Один из экспериментов получил название CDF (Collider Detector of Fermilab), а другой — название D0, являющееся обозначением точки соударения протонов с антипротонами, в которой был установлен детектор. В обоих экспериментах широко проводился поиск новых частиц и физических процессов, но в начале 1990-х годов все было нацелено на поиск Святого Грааля — обнаружение топ-кварка. Каждая коллаборация стремилась первой найти его.
Многие тяжелые частицы нестабильны и практически мгновенно распадаются. В этом случае экспериментаторы ведут поиск не самой частицы, а ее продуктов распада. Например, t-кварк распадается на d-кварк и W (заряженный калибровочный бозон, являющийся переносчиком слабого взаимодействия). В свою очередь, W распадается либо на лептоны, либо на кварки. Таким образом, в экспериментах по поиску топ-кварка ищут d-кварк в сочетании с другими кварками или лептонами.
Однако частицы не рождаются с бирками, на которых написано их имя, поэтому детекторы должны идентифицировать их по отличительным свойствам, например, значению электрического заряда, или взаимодействиям, в которых они участвуют, и регистрация этих свойств происходит в разных частях детектора. Два детектора CDF и D0 разделены на сегменты, каждый из которых фиксирует разные характеристики частиц. Один сегмент, трекер, детектирует заряженные частицы по электронам от ионизованных атомов, образующихся на пути этих частиц. Другой сегмент, называемый калориметром, измеряет энергию, выделяемую частицами при прохождении сквозь детектор. У детекторов есть и другие компоненты, которые могут идентифицировать частицы с иными характерными отличительными свойствами, например b-кварк, живущий до распада дольше большинства других частиц.
Как только детектор регистрирует сигнал, он передает его по сложной системе проводов и усилителей и записывает соответствующие данные. Однако не все, что детектируется, стоит того, чтобы это записывать. При столкновении протона и антипротона интересные частицы вроде топ- и антитоп-кварков рождаются очень редко. Значительно чаще в результате соударений возникают только более легкие кварки и глюоны и, следовательно, не происходит ничего, представляющего интерес. На самом деле на каждый топ-кварк, образованный в Фермилабе, приходилось десять триллионов событий соударений, не содержавших топ-кварк.
Ни одна вычислительная система не имеет достаточной мощности для того, чтобы выделить одно интересное событие среди такой кучи бесполезных данных. Поэтому экспериментаторы всегда используют триггеры — устройства, в которых сами компьютеры и заложенные в них программы действуют как вышибалы в ночном клубе и позволяют записывать только потенциально интересные события. Триггеры в CDF и D0 свели число событий для дальнейшего просеивания к одному на сто тысяч. Это все еще трудная задача, но намного легче поддающаяся обработке, чем одно искомое событие на десять триллионов бесполезных.

Как только информация записана, физики приступают к ее интерпретации и пытаются реконструировать те частицы, которые возникали в каждом интересном соударении. Так как соударений и частиц всегда много, а число блоков информации всегда ограничено, реконструкция результата соударения представляет невероятно сложную задачу, заставляющую людей проявлять всю свою находчивость и мастерство и часто приводящую к новым успехам в обработке данных в дальнейшем.
В 1994 году несколько рабочих групп на CDF нашли события, выглядевшие как рождение топ-кварка (например, показанное на рис. 54), но окончательной уверенности не было. Хотя коллаборация CDF не могла с уверенностью утверждать, что они обнаружили топ-кварк, обе коллаборации D0 и CDF в 1995 году подтвердили открытие. Мой друг Дариен Вуд, работавший на D0, описывал накал страстей на заключительном заседании редакционного совета, на котором ученые подвели итоги анализа данных и представили статью с сообщением о полученных результатах. Заседание продолжалось всю ночь и следующий день, так что люди периодически дремали за своими столами.
Коллективы D0 и CDF совместно разделили честь открытия топ-кварка. Была рождена новая частица, которую никто ранее не видел. Эта частица встала в один ряд с другими частицами, установленными Стандартной моделью. Сейчас уже наблюдено так много топ-кварков, что мы очень точно знаем массу топ-кварка и другие его свойства. В будущем мы ожидаем, что коллайдеры с большей энергией будут рождать так много топ-кварков, что существует опасность, что сами топ-кварки станут фоном, препятствующим открытию других частиц.
Почти наверняка там проявится новая физика. Ниже мы узнаем, почему нерешенные проблемы Стандартной модели говорят нам, что новые частицы и физические процессы должны возникать, когда энергии коллайдеров лишь чуть-чуть превысят те, которые доступны в настоящее время. Эксперименты на Большом адронном коллайдере (БАК) будут искать свидетельства о наличия структуры за пределами Стандартной модели. Если эти эксперименты окажутся успешными, награда будет сказочной — мы добьемся лучшего понимания фундаментальной структуры всей материи. Высокие энергии, соударения многих частиц и умные идеи дадут совместный вклад в решение этой трудной задачи.
Точные тесты Стандартной модели
Перенесемся ненадолго из равнин Иллинойса в гористую Швейцарию, где находится ЦЕРН[108]. Предсказания Стандартной модели проверялись во многих экспериментах, но самыми впечатляющими были эксперименты, проделанные между 1989 и 2000 годами на Большом электрон-позитронном коллайдере (LEP или по-русски ЛЭП), находящемся в ускорительном центре ЦЕРНа. Место для ЦЕРНа было выбрано за его центральное положение в Европе. Главный вход в ЦЕРН находится так близко к границе Франции, что разделяющая две страны сторожевая находится стоит почти рядом с ним. Многие работники ЦЕРНа живут во Франции и дважды в день пересекают границу. При этом они редко испытывают неудобства, разве что их автомобиль не удовлетворяет швейцарским стандартам и Швейцария не разрешает им въезд в страну. Единственная другая опасность, как может подтвердить один коллега — быть рассеянным. Охрана задержала и обыскала этого профессора, когда он не остановился на границе, так как был поглощен мыслями о черных дырах.
Трудно придумать большую разницу в местоположении ЦЕРНа и Фермилаба. ЦЕРН находится по соседству с прекрасными горами Юры (рис. 55), у подножия Монблана, высочайшей горы в Европе, и от него можно быстро доехать до Шамони — замечательной долины, пролегающей между горами, покрытыми ледниками, которые спускаются практически к самой дороге (хотя все ниже и ниже из-за глобального потепления). Многие физики, которым повезло работать в ЦЕРНе, всю зиму ходят с загорелыми лицами, несмотря на постоянные облака над городом, так как у них есть возможность проводить время, катаясь на лыжах, сноубордах или ходить по горам.
ЦЕРН был основан после Второй мировой войны в атмосфере зарождающегося международного сотрудничества. Первыми двенадцатью членами организации стали Западная Германия, Бельгия, Дания, Франция, Италия, Греция, Норвегия, Великобритания, Швеция, Швейцария и Югославия (вышла в 1961 году). Затем к этим странам присоединились Австрия, Испания, Португалия, Финляндия, Польша, Венгрия, Чехословакия и Болгария. Страны-наблюдатели, участвующие в деятельности ЦЕРНа, включают Индию, Израиль, Японию, Российскую Федерацию, Турцию и США. ЦЕРН — поистине международное предприятие.

Как и за Тэватроном, за ЦЕРНом числится много достижений. В 1984 году Карло Руббиа и Симон ван дер Меер получили Нобелевскую премию за создание в ЦЕРНе уникального коллайдера и открытие слабых калибровочных бозонов — этот успех разрушил монополию США на открытия в мире элементарных частиц. Именно сотрудник ЦЕРНа англичанин Тим Бернерс-Ли выдвинул идею Всемирной паутины (WWW), HTML (Hypertext Markup Language) и http (hypertext transfer protocol). Паутина была создана так, что многие экспериментаторы из стран-участниц могли быть одновременно подключены к информации, причем данные могли быть поделены между многими компьютерами. Конечно, последствия создания паутины вышли далеко за пределы ЦЕРНа — часто трудно предвидеть практические применения научного исследования.
В ближайшие несколько лет ЦЕРН будет средоточием ряда самых волнующих физических достижений. Там вступит в строй Большой адронный коллайдер [109], на котором можно будет достичь энергии ускоренных частиц в семь раз большей текущей энергии Тэватрона. Любое открытие, сделанное на БАК, почти неизбежно будет качественно новым. В экспериментах на БАК будут искать, и, скорее всего, обнаружат неизвестную до сих пор физику, лежащую в основе Стандартной модели, которая подтвердит или опровергнет модели типа тех, которые я описываю в этой книге. Хотя коллайдер находится в Швейцарии, БАК будет поистине интернациональным проектом; в настоящее время эксперименты для БАК разрабатываются во всем мире.
Но вернемся в 1990-е годы, когда физики и инженеры смогли построить в ЦЕРНе невероятный Большой электрон-позитронный коллайдер ЛЭП (LЕР) — фабрику Z-бозонов, производившую миллионы Z. Калибровочный Z-бозон — это один из трех калибровочных бозонов, переносящих слабые взаимодействия. Изучив миллионы Z, экспериментаторы на ЛЭП (а также в Станфордском линейном ускорительном центре SLАС в Пало-Альто, Калифорния) смогли осуществить очень точные измерения свойств Z-бозона и с невероятной точностью протестировать предсказания Стандартной модели. Мы бы слишком далеко отклонились от своего пути, если бы я стала детально описывать каждое из этих измерений, но я задержусь на мгновенье, чтобы дать вам ощущение, какая поразительная точность была достигнута в этих экспериментах.
Основное допущение, лежавшее в основе проверки Стандартной модели, было очень простым. Стандартная модель предсказывает массы слабых калибровочных бозонов, а также распады и взаимодействия фундаментальных частиц. Можно проверить согласованность теории слабых взаимодействий, если убедиться, что все соотношения между этими многочисленными величинами удовлетворяют теоретическим предсказаниям. Если бы существовала новая теория с новыми частицами и новыми взаимодействиями, которые стали бы важными при энергиях вблизи масштаба слабых взаимодействий, то возникли бы новые вклады, которые могли бы привести к отклонению предсказаний теории слабых взаимодействий от их значений в рамках Стандартной модели.
Таким образом, в моделях, выходящих за рамки Стандартной модели, получаются предсказания для свойств Z-бозона, слегка отличающиеся от тех, которые даются самой Стандартной моделью. В начале 1990-х годов для предсказания проверяемых свойств Z-бозонов в этих альтернативных моделях все использовали чудовищно громоздкий метод. В этот метод было очень трудно вникнуть, а его описание занимало такое число страниц, что я еле унесла этот документ. В то время я работала ассистентом в Калифорнийском университете в Беркли. Летом 1992 года, когда я принимала участие в летнем совещании в Фермилабе, мне пришло в голову, что не может быть, чтобы связи между различными физическими величинами были столь громоздкими, как предполагалось этим многостраничным документом.
Вместе с Митчем Голденом, в то время ассистентом в Фермилабе, мы разработали более компактный способ интерпретации экспериментальных результатов в слабых взаимодействиях. Митч и я показали, как можно систематически включить эффекты новых тяжелых (до того времени не обнаруженных) частиц, добавляя в Стандартную модель всего лишь три новые величины, суммирующие все возможные вклады от моделей, отличающихся от Стандартной модели. Я провела несколько недель, пытаясь получить все это напрямую, и в конце концов интенсивная работа увенчалась успехом. Было необычайно приятно обнаружить, как можно элегантно связать все процессы, которые могут измерить Z-фабрики. Митч и я ощущали, что нам удалось разработать намного более элегантную картину связи теории и эксперимента. Все это доставляло большое удовлетворение. Однако мы не были одиноки в своем открытии. Одновременно с нами Майкл Пескин и его ассистент Такео Такеучи проделали аналогичную работу, и вскоре по нашему пути последовали другие ученые.
Но реальная история успехов относится к невероятно точным проверкам Стандартной модели на ускорителе ЛЭП. Я не буду вдаваться в детали, а расскажу две истории, которые продемонстрируют поразительную чувствительность экспериментов. Первая история касается установления точной энергии, при которой происходит соударение электронов и позитронов. Экспериментаторам необходимо было знать эту энергию, чтобы определить точное значение массы Z-бозона. Они учли все, что могло повлиять на значение этой энергии. Но даже после того как было учтено все, что только могло прийти в голову, они видели, что когда измерения проводились в определенное время, энергия частиц плавно увеличивалась и уменьшалась. Что было причиной вариаций?
Невероятно, но оказалось, что причиной были приливы в Женевском озере. Благодаря приливам и затяжным дождям в том году, уровень воды в озере то поднимался, то падал. Это, в свою очередь, оказывало влияние на окружающую местность, и в результате слегка изменяло расстояние, которое электроны и позитроны проходили в коллайдере. Как только приливный эффект был учтен, фиктивная зависимость массы Z от времени исчезла.
Вторая история также сильно впечатляет. Электроны и позитроны в коллайдере удерживаются на своих орбитах сильными магнитными полями, которые, в свою очередь, требуют большой затраты энергии. Периодически казалось, что электроны и позитроны слегка теряют регулировку, что указывало на небольшое изменение магнитных полей в коллайдере. Работник на ускорителе заметил, что эти вариации хорошо совпадают с прохождениями экспресса TGV Женева— Париж. По-видимому, возникали скачки мощности, связанные с постоянным током, которые слегка нарушали работу ускорителя. Работавший в ЦЕРНе физик из Парижа Ален Блондель рассказал мне самую забавную часть этой истории. Экспериментаторы получили реальную возможность с абсолютной достоверностью проверить эту гипотезу. Так как большинство служащих на TGV были французами, у них возникла неизбежная забастовка, так что экспериментаторы получили свободный от всплесков день!
Что стоит запомнить
• Самой важной экспериментальной установкой для изучения физики частиц является ускоритель частиц высокой энергии. Коллайдеры высокой энергии — это ускорители частиц, в которых частицы сталкиваются друг с другом. Если энергия частиц достаточно велика, то коллайдеры рождают частицы, которые слишком массивны для того, чтобы существовать в окружающем нас мире.
• Тэватрон — действующий в настоящее время коллайдер, сталкивающий протоны и антипротоны с суммарной энергией 2 ТэВ.
• Большой адронный коллайдер (БАК) в Швейцарии, энергия которого будет в семь раз больше энергии Тэватрона[110], будет способен проверить многие модели физики частиц.
Глава 9
Симметрия: важный организующий принцип
La.
La la la la.
La la la la.
La la la la la la la la la.
Simple Minds[111]
Афина выпустила из клеток полетать трех из своих сов. К несчастью, в тот день Икар оставил открытым верх своего автомобиля, и любопытные совы залетели внутрь салона. Самая озорная из них стала клевать обивку салона и немного ее поцарапала.
Увидев эти царапины, Икар ворвался в комнату Афины и потребовал, чтобы она впредь внимательнее следила за своими совами. Афина возразила, что почти все ее совы отличаются хорошим поведением, и только с одной из них нужно не спускать глаз, но к тому времени все совы уже сидели в своих клетках, и ни Икар, ни Афина не могли определить, которая из сов испортила обивку салона.
Стандартная модель работает на удивление хорошо, но только потому, что она является теорией, в которой кварки, лептоны и слабые калибровочные бозоны — заряженные W и нейтральный Z, являющиеся переносчиками слабого взаимодействия между слабо заряженной материей, — все имеют массу. Конечно, масса фундаментальных частиц критично важна для всего, что есть во Вселенной. Если бы материя была действительно безмассовой, она не могла бы создавать твердые тела, а структура и жизнь во Вселенной, которые мы знаем, никогда бы не возникли. Но слабые калибровочные бозоны и другие фундаментальные частицы в простейшей теории взаимодействий выглядят так, как будто они должны быть безмассовыми и перемещаться в пространстве со скоростью света.
Вам, может быть, покажется странным, что теория взаимодействий предпочитает нулевые массы. Почему не разрешены любые массы? Однако самая фундаментальная квантовая теория взаимодействующих полей в этом отношении непреклонна. Она явно запрещает любые ненулевые значения масс фундаментальных частиц Стандартной модели. Один из триумфов Стандартной модели — обоснование того, как решить эту проблему и создать теорию, в которой частицы имеют те массы, которые они должны иметь согласно наблюдениям.
В следующей главе мы опишем механизм, благодаря которому частицы приобретают массы, — явление, известное как механизм Хиггса. А в этой главе мы обсудим важное понятие симметрии. Симметрия и нарушение симметрии позволяют определить, каким образом Вселенная перешла из состояния бесструктурной точки к наблюдаемой сейчас сложной структуре. Механизм Хиггса тесно связан с симметрией, в частности с нарушенной симметрией. Понимание того, как элементарные частицы приобретают массы, требует знакомства с этими важными идеями.
Вещи, которые изменяются, оставаясь прежними
Для большинства физиков симметрия — священное слово. Можно предположить, что и другие сообщества людей высоко ценят симметрию, так как и христианский крест и иудейская менора, и колесо кармы в буддизме, и мусульманский полумесяц, и индуистская мандала — все обладают симметрией (рис. 56). Говорят, что некая вещь обладает симметрией, если вы можете манипулировать этой вещью, например вращать ее, отражать в зеркале или менять местами отдельные части, и при этом новая конфигурация неотличима от исходной. Например, если вы поменяете местами две одинаковые свечи в меноре, вы не увидите разницы. Отражение креста в зеркале идентично самому кресту.

Если мы говорим о математике, физике или мире в целом, мы можем совершать преобразования, которые при наличии симметрии, кажется, не меняют ничего. Система обладает симметрией, если при обмене местами ее компонент, отражении ее в зеркале или при вращении на полный оборот не заметно никакой разницы, если посмотреть на систему снова после преобразований.
Часто симметрия является статическим свойством. Например, симметрия креста не включает времени. Однако физики часто предпочитают описывать симметрии с помощью так называемых преобразований симметрии — манипуляций, которые можно совершить с системой, не изменяя ни одного из ее наблюдаемых свойств. Например, вместо того, чтобы говорить, что свечи в меноре эквивалентны, можно сказать, что менора не изменит своего вида, если поменять местами две свечи. На самом деле, чтобы заявить, что имеется симметрия, необязательно реально менять свечи местами. Если мысленно поменять свечи, не будет видно никакой разницы. Иногда для простоты я буду описывать симметрию именно таким образом.
Мы все знакомы с примерами симметрии не только в науке и священных символах, но и в светском искусстве. Симметрию можно обнаружить в большинстве произведений живописи, скульптуры, в архитектурных сооружениях, в музыке, танце и поэзии. Возможно, самым поразительным в этом отношении является исламское искусство с его богатым использованием симметрии в архитектуре и орнаментальном искусстве, что может подтвердить каждый, видевший дворец Тадж Махал. Здание не только выглядит одинаково со всех сторон, оно идеально отражается в спокойной глади воды длинного бассейна перед входом во дворец. Даже деревья были посажены так, чтобы сохранить симметрии монумента. Когда мне довелось быть там, я заметила гида, показывающего некоторые точки симметрии, и попросила его показать мне остальные. Я осмотрела здания с удивительных точек, с трудом карабкаясь по каменистой кладке на углу площади, для того чтобы увидеть все симметрии, которыми обладает монумент.
В разговорной речи люди часто отождествляют симметрию с красотой. Действительно, определенное восхищение симметрией возникает из регулярности и аккуратности, которые она обеспечивает. Симметрия также помогает процессу обучения, так как повтор в пространстве или во времени создает в нашей голове прочные образы. Запрограммированный отклик мозга на симметрию и ее явная эстетическая привлекательность во многом являются причиной того, что мы окружаем себя симметрией.
Однако симметрии возникают не только в живописи и архитектуре, но и в природе, причем без всякого вмешательства человека. Поэтому вы так часто сталкиваетесь с симметриями в физике. Цель физики — связать друг с другом различные величины так, чтобы на основе наблюдений можно было делать предсказания. В этом смысле симметрия является естественным участником игры. Если физическая система обладает симметрией, вы можете описать систему на основе меньшего числа наблюдений, чем если бы у системы не было симметрии. Например, если имеются два тела с одинаковыми свойствами, я буду знать физические законы, управляющие поведением одного из тел, если я уже исследовала поведение другого. Так как два тела эквивалентны, я знаю, что они должны вести себя одинаково.
В физике существование преобразования симметрии в системе означает, что существует определенная процедура перегруппировки системы, оставляющая неизменными все ее измеримые физические свойства[112]. Например, если система обладает вращательной и трансляционной симметриями, двумя хорошо известными примерами симметрий пространства, то физические законы выглядят одинаково во всех направлениях и во всех местах. Вращательная и трансляционная симметрии говорят, например, что не имеет значения, в какую сторону вы смотрите или где вы находитесь в момент, когда вы ударяете бейсбольной битой по мячу, — если во всех случаях приложенная сила одинакова, мяч будет вести себя одинаково. Любой эксперимент будет приводить к одному и тому же результату, если вы повернете свою установку или повторите измерение в другой комнате или другом месте.
Трудно переоценить важность симметрии в физических законах. Многие физические теории, такие как законы электродинамики Максвелла или теория относительности Эйнштейна, глубоко уходят корнями в симметрию. Используя различные симметрии, мы можем обычно упростить задачу использования теорий для получения физических предсказаний. Например, предсказание орбитального движения планет, гравитационное поле Вселенной (оно более или менее симметрично относительно вращений), поведение частиц в электромагнитных полях и много других физических явлений становятся математически проще, если принять во внимание симметрию.
Симметрии в физическом мире не всегда полностью очевидны. Но даже если симметрии не до конца ясны или являются всего лишь теоретическими инструментами, они обычно сильно упрощают формулировку физических законов. Не является исключением и квантовая теория взаимодействий, к рассмотрению которой мы вскоре перейдем.
Внутренние симметрии
В общем случае физики разделяют симметрии по разным категориям. Вероятно, вы больше всего знакомы с симметриями пространства, т. е. преобразованиями, которые передвигают или вращают предметы внешнего мира. Эти симметрии, включающие уже упомянутые вращательную и трансляционную симметрии, утверждают, что законы физики одинаковы для систем, независимо от того, в какую сторону они повернуты и в каком месте находятся.
Теперь я хочу рассмотреть другой тип симметрии, известный под названием внутренней симметрии. В то время как пространственные симметрии говорят нам, что физика рассматривает все направления и все положения в пространстве как одинаковые, внутренние симметрии говорят о том, что физические законы действуют одинаковым образом на различные, но эффективно неразличимые тела. Иначе говоря, преобразования внутренней симметрии меняют местами или перемешивают тела так, что это остается незамеченным. В действительности, я уже приводила пример внутренней симметрии — возможность перемены местами свечей в меноре. Внутренняя симметрия утверждает, что две свечи эквивалентны. Это утверждение касается свечей, а не пространства.
Однако традиционная менора обладает как пространственной, так и внутренней симметриями. Если свечи эквивалентны, что означает наличие внутренней симметрии, сама менора выглядит одинаково, если ее повернуть на 180° вокруг центральной свечи, что означает наличие пространственной симметрии. Но внутренняя симметрия может существовать даже при отсутствии симметрии пространства. Например, вы можете поменять местами одинаковые зеленые плитки в мозаике, даже если выложенный этими плитками лист имеет нерегулярную форму.
Другой пример внутренней симметрии — взаимозаменяемость двух тождественных красных шариков. Если вы держите в каждой, руке по одному такому шарику, не имеет значения, в какой руке какой шарик находится. Даже если вы пометите их цифрами 1 и 2, вы никогда не узнаете, не поменяла ли я их как-нибудь незаметно местами. Обратите внимание, что пример с шариками не связан ни с каким пространственным расположением этих шариков в том смысле, в каком говорилось в примерах с менорой и мозаикой. Внутренние симметрии относятся к самим телам, а не к их расположению в пространстве.
Физика частиц имеет дело с несколько абстрактными внутренними симметриями, которые связывают разные типы частиц. Эти симметрии рассматривают частицы и создающие их поля как взаимозаменяемые. Так же как два тождественных шарика ведут себя совершенно одинаково, если покатить их или ударить об стену, частицы двух типов, имеющие одинаковые заряды и массы, подчиняются одинаковым физическим законам. Описывающая это симметрия называется симметрией ароматов.
В гл. 7 мы видели, что ароматы — это три различных типа частиц, которые обладают одинаковыми зарядами и входят в одно из трех поколений. Например, электроны и мюоны — это два аромата заряженных лептонов, и это означает, что их заряды тождественны. Если бы мы жили в мире, в котором электрон и мюон имели бы вдобавок одинаковые массы, эти две частицы были бы полностью неразличимыми. Тогда они обладали бы симметрией по ароматам, согласно которой электрон и мюон в присутствии любых других частиц или взаимодействий должны вести себя тождественно.
В нашем мире мюон тяжелее электрона, так что симметрия по ароматам является неточной. Однако для ряда физических предсказаний разность масс может быть несущественной, так что симметрии по ароматам между легкими частицами с тождественными зарядами, типа мюона и электрона, часто оказываются полезными при вычислениях. Иногда использование даже слегка неидеальных симметрий помогает получить при расчетах довольно точные результаты. Например, разность масс между частицами часто так мала (по сравнению с энергией или какой-то большой массой), что она не вносит заметной разницы в предсказания.
Однако наиболее важным для нас типом симметрии является сейчас симметрия, относящаяся к теории взаимодействий частиц и являющаяся точной. Такая симметрия также является внутренней симметрией среди частиц, но она несколько более абстрактна, чем только что обсуждавшаяся симметрия по ароматам. Этот конкретный тип внутренней симметрии можно продемонстрировать на следующем примере. Как вы, возможно, помните из курса средней школы, видели в театре или на занятиях живописью, три световых луча, обычно красный, зеленый и синий, соединяясь вместе, образуют луч белого света. Если мы поменяем местами положения трех таких цветных прожекторов, при любом их расположении установка будет давать белый свет. До тех пор пока нас интересует только конечный результат — белый свет, нам все равно, где возник каждый луч. В этом случае преобразование внутренней симметрии, меняющее местами разные прожекторы, никогда не приведет к каким-либо наблюдаемым следствиям.
Сейчас мы увидим, что есть тесная связь между этой симметрией и симметриями, связанными с взаимодействиями, так как в обоих случаях вы не можете ничего наблюдать. Световая установка демонстрирует симметрию только потому, что мы не видим ничего, кроме смешанного света. Если бы можно было видеть отдельные световые лучи, мы бы знали, как они поменялись местами. Как указывалось выше, тесная аналогия между цветами и взаимодействиями есть причина для использования терминов «цвет» и «квантовая хромодинамика» (КХД) при описании сильного взаимодействия.
В 1927 году физики Фриц Лондон и Герман Вейль показали, что простейшее описание взаимодействий на языке квантовой теории поля содержит внутренние симметрии, аналогичные симметриям цветных прожекторов. Связь между взаимодействиями и симметрией весьма хитроумна, поэтому обычно о ней можно прочитать только в научных книгах. Так как детали этой связи вам не нужны, чтобы понимать далее вопросы, связанные с массой, в том числе механизм Хиггса и проблему иерархии, можно при желании сразу перейти к следующей главе. Но если вас интересует роль внутренней симметрии в теории взаимодействий и механизме Хиггса, то читайте дальше.
Симметрии и взаимодействия
Все взаимодействия — электромагнитное, слабое и сильное — содержат внутренние симметрии. (Гравитация связана с симметриями пространства и времени и поэтому должна рассматриваться отдельно.) Если бы не внутренние симметрии, квантовая теория взаимодействий была бы непроходимым болотом. Чтобы понять эти симметрии, необходимо сначала рассмотреть поляризации калибровочных бозонов.
Возможно, вы знакомы с понятием поляризации света. Например, поляризующие солнечные очки уменьшают яркость света, пропуская только свет с вертикальной поляризацией и не пропуская свет с горизонтальной поляризацией. В данном случае поляризации — это независимые направления, в которых могут колебаться электромагнитные волны.
Квантовая механика связывает с каждым фотоном волну. Для каждого отдельного фотона также возможны различные поляризации, однако не все мыслимые поляризации разрешены. Оказывается, что когда фотон распространяется в каком-то направлении, волна может колебаться только в направлениях, перпендикулярных направлению ее движения. Эта волна ведет себя так же, как океанская волна, которая тоже колеблется в перпендикулярном направлении. Именно поэтому вы видите колебания вверх-вниз буйка или привязанной лодки, когда проходит волна.
Волна, связанная с фотоном, может колебаться в любом направлении, перпендикулярном ее направлению движения (рис. 57). На самом деле существует бесконечное число таких направлений. Вообразите окружность, перпендикулярную линии движения. Можно убедиться, что волна способна осциллировать в любом радиальном направлении (от центра окружности наружу), и таких направлений бесконечно много.

Но при физическом описании этих колебаний нам нужны только два независимых взаимно перпендикулярных колебания, что позволяет учесть все возможности. На языке физики эти колебания называются поперечными поляризациями. Представьте, что вы ввели оси координат x и у с началом в центре окружности. Какую бы линию вы не провели из центра окружности, она всегда пересечет окружность в определенном месте, соответствующем определенной паре значений x и у, поэтому это место может быть однозначно задано всего лишь двумя координатами. Аналогично (не вдаваясь в детали того, как это получается), хотя существует бесконечное число направлений, перпендикулярных направлению распространения волны, все эти направления можно получить из комбинаций световых пучков, поляризованных в любых двух взаимно перпендикулярных направлениях.
Важно то, что в принципе могло бы существовать и третье направление поляризации, когда колебания происходят вдоль направления движения волны (если такая поляризация существует, ее называют продольной поляризацией). Например, так распространяется звуковая волна. Однако у фотона такой поляризации не существует. В природе существуют только две из трех возможных независимых направлений поляризаций. Фотон никогда не совершает колебаний вдоль направления своего движения или в направлении времени; он совершает колебания только в направлениях, перпендикулярных направлению своего движения.
Даже если бы мы не знали из независимых теоретических соображений, что продольная поляризация невозможна, квантовая теория поля требует исключить ее. Если бы физику пришлось делать вычисления, используя теорию взаимодействий, ошибочно включающую все три направления поляризации, предсказания теории не имели бы смысла. Например, такая теория предсказывала бы абсурдно большие вероятности взаимодействий калибровочных бозонов. А именно, она бы предсказывала существование калибровочных бозонов, взаимодействующих чаще, чем всегда, т. е. более 100 % времени. Любая теория, делающая такие бессмысленные предсказания, очевидным образом неверна, так что и квантовая теория, и сама природа ясно указывают, что неперпендикулярная поляризация не существует.
К сожалению, простейшая теория взаимодействий, которую могут сформулировать физики, включает это фиктивное направление поляризации. Это и не удивительно, так как теория, которая должна работать для каждого фотона, не может содержать информацию об одном конкретном фотоне, распространяющемся в конкретном направлении. А без такой информации специальная теория относительности не выделит никакое направление. В теории, которая сохраняет симметрии специальной теории относительности (включая вращательную симметрию), нужно иметь три, а не два направления, чтобы описать все направления, вдоль которых может колебаться фотон. При таком описании фотон может колебаться вдоль любого направления в пространстве.
Но мы знаем, что это неверно. Для любого конкретного фотона его направление движения выделено и колебания в этом направлении запрещены. Но вы же не собираетесь строить отдельную теорию для каждого отдельного фотона со своим отдельным направлением движения. Вам нужна теория, работающая вне зависимости от того, куда движется фотон. Хотя можно попробовать построить теорию, вообще не содержащую фиктивного направления поляризации, было бы значительно проще и яснее сохранить вращательную симметрию и исключить плохую поляризацию как-нибудь иначе. Физики, стремящиеся к простоте, заметили, что квантовая теория поля работает хорошо, если включить в нее фиктивную продольную поляризацию, но добавить дополнительное слагаемое, чтобы отфильтровать хорошие, физически приемлемые предсказания от плохих.
Именно в этом месте в игру вступают внутренние симметрии. Роль внутренних симметрий в теории взаимодействий состоит в устранении противоречий, которые могут создать нежелательные поляризации, не расплачиваясь за это симметриями специальной теории относительности. Введение внутренних симметрий — это простейший путь отсеять поляризацию вдоль направления движения, которую исключают независимые теоретические соображения и экспериментальные наблюдения. Внутренние симметрии делят поляризации на хорошие и плохие, т. е. на те, которые совместимы с симметриями, и те, которые с ними не совместимы. Объяснить, как это происходит, технически довольно трудно, но чтобы дать вам общую идею, я попытаюсь воспользоваться аналогией.
Предположим, что у вас есть швейная машинка, способная шить рубашки с рукавами двух размеров — короткими и длинными, но по каким-то причинам изобретатель этой машинки забыл включить контролирующее устройство, обеспечивающее, чтобы левые и правые рукава рубашки были одного размера. Половину времени вы будете шить нормальные рубашки с двумя длинными или двумя короткими рукавами. Однако вторую половину времени вы будете производить бесполезную продукцию — рубашки с одним коротким и одним длинным рукавами. К сожалению, другой швейной машинки у вас нет.
У вас есть выбор: либо выбросить вашу швейную машинку и вообще не шить рубашек, либо оставить машинку и шить половину хороших рубашек и половину негодных. Однако не все потеряно, так как довольно очевидно, какие рубашки надо оставить: годятся только те, которые сохраняют лево-правую симметрию. Вы будете всегда нормально одеты, если будете шить на вашей швейной машинке все типы рубашек, а затем отберете те из них, которые обладают лево-правой симметрией.
Внутренняя симметрия, связанная с взаимодействиями, работает похожим образом. Она предоставляет удобный критерий, позволяющий отличить те величины, которые мы в принципе можем наблюдать (те, которые обладают поляризацией, которую мы хотим сохранить), от тех, которые не должны присутствовать (т. е. тех, которым присуща фиктивная продольная поляризация вдоль направления движения). Как и в случае фильтров спама в компьютерах, которые выискивают отличительные черты нежелательных электронных писем, с тем чтобы отделить их от полезных посланий, фильтр внутренних симметрий отличает физические процессы, сохраняющие симметрию, от фиктивных процессов, которые ее нарушают. С помощью внутренних симметрий легко отличить спамоподобные поляризации — если они есть, они нарушают внутреннюю симметрию.
То, каким образом работает симметрия, очень похоже на разобранный выше пример с цветными прожекторами, в котором мы могли наблюдать только свет, образованный смешением трех цветов, а не отдельные цветные лучи. Аналогично, оказывается, что только определенные комбинации частиц совместимы с внутренними симметриями, содержащимися в теории взаимодействий, и именно эти комбинации возникают в физическом мире.
Внутренние симметрии, связанные с взаимодействиями, запрещают любой процесс, включающий плохие поляризации, т. е. те, которые осциллируют вдоль направления движения (и реально не встречаются в природе). Так же как криво сшитые рубашки, несовместимые с лево-правой симметрией, немедленно различаются и выкидываются, так и фиктивные поляризации, несовместимые с внутренней симметрией, автоматически отбрасываются и никогда не мешают вычислениям. Теория, которая в качестве обязательного условия выдвигает правильную внутреннюю симметрию, исключает плохие поляризации, которые в противном случае могли бы присутствовать.
Все взаимодействия — электромагнитное, слабое и сильное — передаются калибровочными бозонами: электромагнетизм — фотонами, слабое взаимодействие — слабыми калибровочными бозонами, сильное взаимодействие — глюонами. При этом каждый тип калибровочного бозона связан с волнами, которые в принципе могут осциллировать во всех трех направлениях, но в действительности осциллируют только в перпендикулярных направлениях. Таким образом, для того чтобы исключить плохие поляризации калибровочных бозонов, переносящих данное взаимодействие, нужна своя симметрия. Следовательно, существует отдельная симметрия, связанная с электромагнетизмом, независимая симметрия, связанная со слабым взаимодействием, и еще одна симметрия, связанная с сильным взаимодействием.
Внутренние симметрии в теории взаимодействий могут показаться сложными, но это простейший известный физикам путь к формулировке содержательной квантово-полевой теории взаимодействий, позволяющий делать какие-то предсказания. Внутренние симметрии различают истинные и фиктивные поляризации.
Внутренние симметрии, которые были только что рассмотрены, играют критически важную роль в теории взаимодействий. Они же лежат в основе механизма Хиггса, показывающего, каким образом элементарные частицы в Стандартной модели приобретают массу. В следующей главе нам не потребуются детали внутренней симметрии, однако мы увидим, что симметрия (и ее нарушение) являются существенными компонентами Стандартной модели.
Калибровочные бозоны, частицы и симметрия
До сих пор мы рассматривали влияние симметрии только на калибровочные бозоны. Но преобразования симметрии, связанные с взаимодействием, действуют не только на калибровочные бозоны. Такой бозон взаимодействует с частицами, испытывающими связанное с этим бозоном взаимодействие: фотон взаимодействует с электрически заряженными частицам, слабые бозоны взаимодействуют с частицами, обладающими слабым зарядом, а глюоны взаимодействуют с кварками.
Благодаря этим взаимодействиям каждая внутренняя симметрия может сохраняться только в случае, если она преобразует не только калибровочные бозоны, но и частицы, с которыми они взаимодействуют. Можно провести такую аналогию. Например, вращения не будут преобразованиями симметрии, если они действуют на одни объекты и не действуют на другие. Если вы повернете только верхнюю вафлю пирожного «Орео»[113], а не все пирожное целиком, то вы просто разделите его на две части. Пирожное будет выглядеть после поворота неизменным, только если вы одновременно повернете все его части.
По аналогичным причинам то преобразование, которое преобразует только калибровочные бозоны — переносчики взаимодействия, но не частицы, участвующие в этом взаимодействии, никогда не будет сохранять симметрию. Внутренняя симметрия, исключающая фиктивные поляризации глюонов, требует, чтобы не только глюоны, но и кварки были взаимозаменяемыми. На самом деле преобразование симметрии, меняющее местами кварки, совпадает с преобразованием, меняющим местами калибровочные бозоны. Единственный способ сохранить симметрию — это смешать их вместе, точно так же, как для сохранения симметрии пирожного Орео нужно одновременно повернуть его целиком.
В основном в этой книге нас будет интересовать слабое взаимодействие. Связанная с этим взаимодействием внутренняя симметрия рассматривает три слабых калибровочных бозона как эквивалентные. Она также рассматривает как эквивалентные такие пары, как электрон и нейтрино или иий кварки. Преобразование симметрии слабого взаимодействия меняет местами три калибровочных бозона, а также указанные пары частиц. Как в случае глюонов и кварков, симметрия слабого взаимодействия сохраняется, только когда все меняется местами одновременно.
Что стоит запомнить
• Симметрии указывают, когда две разные конфигурации ведут себя одинаково.
• В физике частиц симметрии полезны как способ запретить некоторые взаимодействия. Те взаимодействия, которые не сохраняют симметрии, не разрешены.
• Симметрии важны в теории взаимодействий, так как самая простая работоспособная теория взаимодействий содержит связанную с каждым взаимодействием симметрию. Эти симметрии исключают нежелательные частицы. Они также исключают неверные предсказания относительно поведения частиц высоких энергий, которые в противном случае следовали бы из теории.
Глава 10
Происхождение масс элементарных частиц: спонтанное нарушение симметрии и механизм Хиггса
One of these mornings the chain is gonna break.
Aretha Franklin[114]
Строгий запрет на превышение скорости превращал в кошмар для Икара III поездки на большие расстояния. Ему нравилось мчаться так быстро, как ему хотелось, но полиция тормозила его чуть ли не каждые полмили. Гаишники никогда не обращали внимания на скучные, обычные машины, а цеплялись только к энергичным автомобилям с турбозарядкой, вроде того, который был у Икара.
Икар решил сам для себя, что он будет ездить только на короткие расстояния от дома, так как в этом случае он мог избежать встречи с полицией. В пределах области радиусом в полмили полиция никогда не вмешивалась, и ему всегда удавалось развить впечатляющую скорость. И хотя вдали от дома мощность мотора его «Порше» оставалась неизвестной, но ближе к дому она стала легендарной.
Симметрии важны, но обычно Вселенная не выглядит идеально симметрично. Слегка неточные симметрии — вот что делает мир интересным (но организованным). С моей точки зрения, одной из самых интригующих сторон физического исследования является поиск связей, наполняющих смыслом симметрию в несимметричном мире.
Когда симметрия неточна, физики говорят, что она нарушена. Хотя нарушенная симметрия часто бывает интересна, эстетически она не всегда привлекательна — могут быть потеряны (или уменьшены) красота и экономичность лежащей в основе системы или теории. Даже очень симметричный Тадж Махал не обладает идеальной симметрией, так как скупой наследник шаха решил не строить запланированный второй монумент, добавив вместо этого лежащую в стороне гробницу. Эта вторая гробница разрушает в остальном идеальную четырехкратную вращательную симметрию Тадж Махала, слегка уменьшая заложенную в его основе красоту.
Однако, к счастью для эстетически развитых физиков, нарушенные симметрии могут быть еще красивее и интереснее, чем идеально симметричные вещи. Идеальная симметрия часто скучна. Мона Лиза с симметричной улыбкой — это было бы совсем не то.
В физике, как и в искусстве, одна простота недостаточна для достижения высшей цели. Жизнь и Вселенная редко идеальны, и почти все симметрии, которые вам придут в голову, нарушены. Хотя мы, физики, ценим симметрию и восхищаемся ею, мы все равно должны найти связь между симметричной теорией и несимметричным миром. Лучшие теоретики признают элегантность симметричных теорий, и в то же время включение механизма нарушения симметрии необходимо для того, чтобы делать предсказания, согласующиеся с происходящими в нашем мире явлениями. Цель состоит в том, чтобы, не теряя элегантности, построить теории, которые оказываются богаче и иногда даже красивее.
Механизм Хиггса, основанный на явлении спонтанного нарушения симметрии (которое мы рассмотрим в следующей главе), дает пример такой хитроумной элегантной теоретической идеи. Этот механизм, названный по имени шотландского физика Питера Хиггса, позволяет частицам Стандартной модели — кваркам, лептонам и слабым калибровочным бозонам — приобрести массу.
Если бы не было механизма Хиггса, все элементарные частицы должны были бы быть безмассовыми; Стандартная модель с массивными частицами и без механизма Хиггса приводила бы к бессмысленным предсказаниям при больших энергиях. Магическое свойство механизма Хиггса заключается в том, что он не только позволяет вам получить свое пирожное, но и съесть его: частицы приобретают массы, но когда энергии достигают значений, при которых массивные частицы приводили бы к проблемам, частицы ведут себя, как если бы они были безмассовыми. Мы увидим, что механизм Хиггса позволяет частицам иметь массу, но свободно двигаться лишь в ограниченной области, что очень напоминает автомобиль Икара, который через полмили останавливает полисмен, но который может двигаться без помех на ограниченные расстояния. Оказывается, этого достаточно для решения проблем при высоких энергиях.
Механизм Хиггса — одна из самых изящных идей в квантовой теории поля, лежащая в основе происхождения масс всех элементарных частиц. Однако она довольно абстрактна. По этой причине она известна, в основном, только специалистам. Хотя многие идеи, которые будут рассмотрены ниже в этой книге, вы сможете понять и без знания деталей механизма Хиггса (так что при желании можно прямо перейти к выводам в конце главы), я бы рекомендовала вам читать дальше и немного углубиться в физику частиц и в идеи типа спонтанного нарушения симметрии, на которые в наши дни опираются теоретические исследования в этой области. В качестве бонуса вы получите поразительное понимание электромагнетизма, пришедшее только в 1960-е годы, когда были должным образом осмыслены слабое взаимодействие и механизм Хиггса. Ниже, когда мы перейдем к рассказу о моделях с дополнительными измерениями, знакомство с механизмом Хиггса позволит вам понять потенциальные достоинства этих современных идей.
Спонтанно нарушенная симметрия
Прежде чем описывать механизм Хиггса, нужно сначала исследовать спонтанное нарушение симметрии — особый тип нарушения симметрии, играющий центральную роль в этом механизме. Спонтанное нарушение симметрии играет большую роль во многих свойствах Вселенной, которые мы уже понимаем, и, вероятно, играет роль в тех свойствах, которые еще предстоит открыть.
Спонтанное нарушение симметрии повсеместно встречается не только в физике, оно является распространенным явлением в повседневной жизни. Спонтанно нарушенная симметрия — это симметрия, которая сохраняется физическими законами, но не способами, которыми вещи реально упорядочены в мире.
Спонтанное нарушение симметрии имеет место тогда, когда система не может сохранить симметрию, которая существовала бы в противном случае. Вероятно, лучший способ объяснить, как это работает, — привести несколько примеров.
Рассмотрим для начала званый обед, на котором гости сидят за круглым столом и между ними стоят стаканы с водой. Какой стакан возьмет кто-то из гостей — справа или слева от него? На это нельзя дать определенного ответа. Мне сказали, что по мнению Мисс Правила Приличия надо брать тот стакан, который справа, но если пренебречь правилами этикета, то в равной степени годится и левый, и правый стакан.
Однако, как только кто-то выберет стакан, симметрия нарушается. Стимул к выбору необязательно должен быть частью системы; это мог бы быть и внешний фактор — жажда. Тем не менее, если кто-то внезапно отопьет глоток из стакана слева от себя, то это же сделают и соседи, так что в конце концов каждый гость выпьет из стакана, стоящего слева.
Симметрия существует до того момента, пока кто-нибудь не возьмет стакан. В этот момент лево-правая симметрия спонтанно нарушается. Ни один закон физики не требует, чтобы кто-то должен был выбрать левый или правый стакан. Но выбор должен быть сделан, и после этого левое и правое становятся неодинаковыми в том смысле, что пропадает симметрия, меняющая левое с правым.
Приведем другой пример. Представьте карандаш, стоящий на своем острие в центре круга. В течение доли секунды, пока карандаш покоится в строго вертикальном положении, для него все направления эквивалентны и существует вращательная симметрия. Но карандаш долго не продержится на своем острие — он спонтанно упадет в некотором направлении. Как только карандаш начинает падать, исходная вращательная симметрия нарушается.
Заметим, что физические законы сами по себе не определяют это направление. Физика падения карандаша будет в точности одинаковой независимо от направления падения. Нарушать симметрию будет сам карандаш, т. е. состояние системы. Карандаш не способен одновременно падать во всех направлениях. Он должен упасть только в одном конкретном направлении.
Бесконечно длинная и высокая стена будет выглядеть одинаково везде и по всем направлениям. Но поскольку настоящая стена имеет границы, то если вы должны увидеть симметрии, вам нужно приблизиться к стене на достаточно малое расстояние, так чтобы границы исчезли из вашего поля зрения. Наличие у стены концов указывает на то, что не все у нее везде одинаково, но если вы прижметесь к стене носом, так что сможете видеть только ее малую область, то будет казаться, что симметрия сохраняется. Стоит немного поразмышлять над этим примером, который показывает, что если смотреть с одного расстояния, симметрия может казаться сохраняющейся, в то время как с другого расстояния она кажется нарушенной. Очень скоро нам станет ясна важность этого понятия.
Почти все симметрии в мире, которые могут прийти вам в голову, не сохраняются. Так, имеется много симметрий, присутствующих в пустом пространстве, например, вращательная или трансляционная инвариантность, говорящие нам, что все направления и положения эквивалентны. Однако пространство не пусто, в нем натыканы структуры вроде звезд и Солнечной системы, занимающие определенные положения и определенным образом ориентированные, так что исходная симметрия разрушается. Эти структуры могут быть где угодно, но не могут быть везде. Исходные симметрии должны быть нарушены, хотя они неявно сохраняются в описывающих мир физических законах.
Связанная со слабым взаимодействием симметрия также спонтанно нарушена. В оставшейся части этой главы я поясню, откуда мы это знаем, и расскажу о некоторых следствиях. Мы увидим, что спонтанное нарушение симметрии слабого взаимодействия есть единственный способ объяснения существования массивных частиц, позволяющий избежать неверных предсказаний для частиц высоких энергий, которых не удается избежать ни в одной другой теории. Механизм Хиггса удовлетворяет как требованию существования связанной со слабым взаимодействием внутренней симметрии, так и требованию необходимости ее нарушения.
Проблема
Слабое взаимодействие обладает одним особенно странным свойством. В противоположность электромагнитному взаимодействию, которое распространяется на большие расстояния (вы убеждаетесь в этом каждый раз, когда включаете радиоприемник), слабое взаимодействие воздействует только на материю, находящуюся поблизости в очень малой окрестности. Чтобы повлиять друг на друга силой, порожденной слабым взаимодействием, две частицы должны находиться на расстоянии 10-16 см друг от друга.
Для физиков, изучавших квантовую теорию поля и квантовую электродинамику (КЭД, квантово-полевая теория электромагнетизма) на заре их развития, такая ограниченная область взаимодействия представлялась загадкой. Благодаря КЭД казалось, что взаимодействия, подобные хорошо понятному электромагнитному, должны переноситься произвольно далеко от заряженного источника. Почему же слабое взаимодействие связывало частицы не на любом расстоянии, а только вблизи?
Квантовая теория поля, соединяющая принципы квантовой механики и специальной теории относительности, требует, что если частицы малых энергий переносят взаимодействия только на малые расстояния, они должны обладать массой, а чем тяжелее частица, тем меньше область ее взаимодействия. Как объяснялось в гл. 6, это есть следствие соотношения неопределенностей и специальной теории относительности. Соотношение неопределенностей утверждает, что для того, чтобы исследовать или оказывать влияние на физические процессы на коротких расстояниях, нужны частицы больших импульсов, а специальная теория относительности связывает импульс с массой. Хотя это утверждение носит качественный характер, квантовая теория поля делает эту связь строгой. Она показывает, как далеко может улететь массивная частица: чем меньше масса, тем больше расстояние.
Таким образом, согласно квантовой теории поля малый радиус слабого взаимодействия может означать только одно — слабые калибровочные бозоны, переносящие слабое взаимодействие, обязаны иметь ненулевую массу. Однако описанная в предыдущей главе теория взаимодействий выполняется только для калибровочных бозонов типа фотона, переносящих взаимодействия на большие расстояния и имеющих нулевую массу. Согласно исходной теории взаимодействий, существование ненулевых масс казалось странным и непонятным — если калибровочные бозоны имеют массу, высокоэнергетические предсказания теории теряют смысл. Например, из теории следовало бы, что массивные калибровочные бозоны очень большой энергии взаимодействовали бы слишком сильно, на самом деле настолько сильно, что частицы казались бы взаимодействующими более 100 % времени. Ясно, что такая наивная теория неверна.
Кроме того, массы слабых калибровочных бозонов, кварков и лептонов (про все эти частицы мы знаем, что их масса отлична от нуля) не сохраняют внутреннюю симметрию, которая, как мы видели в предыдущей главе, является ключевой составной частью теории взаимодействий. Физики, надеявшиеся построить теорию с массивными частицами, несомненно, нуждались в новых идеях.
Физики показали, что единственный способ построить теорию, не содержащую бессмысленных предсказаний о поведении массивных калибровочных бозонов, состоит в спонтанном нарушении симметрии слабого взаимодействия с помощью процесса, называемого механизмом Хиггса. Поясню, почему это так.
Следует вспомнить из предыдущей главы, что одной из причин, по которой мы хотели иметь внутреннюю симметрию, исключавшую одну из трех возможных поляризаций калибровочного бозона, было то, что теория без симметрии приводит к таким же бессмысленным предсказаниям, как и только что упомянутые. Простейшая теория взаимодействий без внутренней симметрии предсказывает, что любой калибровочный бозон большой энергии, независимо от того, имеет ли он массу или нет, взаимодействует с другими калибровочными бозонами слишком часто.
Успешная теория взаимодействий исключает это плохое высокоэнергетическое поведение, запрещая существование поляризации, приводящей к неправильным предсказаниям и на самом деле отсутствующей в природе. Источником неверных предсказаний для рассеяния при высоких энергиях являются фиктивные поляризации, а симметрия позволяет оставить только физические поляризации, которые реально существуют. Симметрия, которая избавляет теорию от несуществующих поляризаций, также исключает неверные следствия, к которым они бы приводили.
Хотя до сих пор я не говорила об этом явно, идея работает только для без-массовых калибровочных бозонов. В противоположность фотонам, масса слабых калибровочных бозонов не равна нулю. Слабые калибровочные бозоны распространяются со скоростью меньше скорости света. И это сводит на нет всю работу.
В то время как безмассовые калибровочные бозоны имеют только две поляризации, реально существующие в природе массивные калибровочные бозоны имеют три поляризации. Один способ понять это различие состоит в том, что безмассовые калибровочные бозоны всегда движутся со скоростью света, откуда следует, что они никогда не находятся в покое. Следовательно они всегда выделяют свое направление движения, так что всегда можно отличить перпендикулярные направления поляризации от поляризации вдоль направления движения. При этом оказывается, что для безмассового калибровочного бозона физические поляризации осциллируют только в двух перпендикулярных направлениях.
А массивные калибровочные бозоны ведут себя иначе. Как все обычные тела, они могут находиться в покое. Но когда массивный калибровочный бозон стоит на месте, невозможно выделить его направление движения. Для покоящегося калибровочного бозона все три направления должны быть эквивалентны. Но если это так, тогда в природе должны существовать все три возможные поляризации. И они действительно существуют.
Даже если вам сложно принять эту логику, экспериментаторы уже наблюдали эффекты, связанные с третьей поляризацией массивного калибровочного бозона, и подтвердили ее существование. Третья поляризация называется продольной поляризацией. Когда массивный калибровочный бозон движется, продольная поляризация соответствует волне, осциллирующей вдоль направления движения, например в направлении, в котором осциллирует звуковая волна.
В случае безмассовых калибровочных бозонов, например фотонов, такой поляризации не существует. Однако для массивных калибровочных бозонов, таких как слабые калибровочные бозоны, третья поляризация есть реальная часть природы. Эта третья поляризация должна быть частью теории слабых калибровочных бозонов.
Поскольку эта третья поляризация есть источник избыточно большой вероятности взаимодействия слабых калибровочных бозонов при больших энергиях, ее существование ставит перед нами дилемму. Мы уже знаем, что для исключения плохого поведения при больших энергиях нужна симметрия. Но эта симметрия позволяет избавиться от неправильных предсказаний путем одновременного исключения третьей поляризации, а эта поляризация существенна для массивного калибровочного бозона и для описывающей его теории. Хотя внутренняя симметрия могла бы исключить плохие предсказания о поведении при высоких энергиях, за это пришлось бы заплатить слишком большую цену — такая симметрия избавилась бы и от массы! Похоже, что симметрия в теории массивных калибровочных бозонов выплескивает вместе с водой и ребенка.
Трудность на первый взгляд кажется непреодолимой, так как требования к теории массивных калибровочных бозонов представляются противоречащими друг другу. С одной стороны, внутренняя симметрия, описанная в предыдущей главе, не должна сохраняться, так как в противном случае массивные калибровочные бозоны с тремя физическими поляризациями были бы запрещены. С другой стороны, без внутренней симметрии, уничтожающей две поляризации, теория взаимодействий дает неверные предсказания для калибровочных бозонов большой энергии. Если мы хотим сохранить хоть какую-то надежду исключить плохое поведение при высоких энергиях, нам все еще нужна симметрия для исключения третьей поляризации каждого массивного калибровочного бозона.
Ключ к разрешению этого кажущегося парадокса и формулировке правильного описания массивных калибровочных бозонов на языке квантовой теории поля заключался в признании различия между бозонами больших и малых энергий. В теории без внутренней симметрии только предсказания, касающиеся калибровочных бозонов высокой энергии, выглядели сомнительными. Предсказания о низкоэнергетических массивных калибровочных бозонах выглядели разумно (и были правильными).
Эти два факта совместно требовали довольно глубокого вывода: чтобы избежать сомнительных предсказаний при больших энергиях, необходима внутренняя симметрия, иными словами, все еще применимы уроки предыдущей главы. Но когда энергия массивного калибровочного бозона мала (по сравнению с той энергией, которая по соотношению Эйнштейна E = mc2 соответствует его массе), симметрия уже не может сохраняться. Эта симметрия должна быть устранена так, чтобы калибровочные бозоны могли иметь массу, а третья поляризация могла участвовать во взаимодействиях при низких энергиях, когда учет массы приводит к различиям.
В 1964 году Питер Хиггс и другие обнаружили, каким образом теории взаимодействий могут включать массивные калибровочные бозоны, проделав в точности то, что мы только что сказали, — сохранив внутреннюю симметрию при больших энергиях, но устранив ее при малых энергиях. Механизм Хиггса, основанный на спонтанном нарушении симметрии, разрушает внутреннюю симметрию слабых взаимодействий только при низкой энергии. Это обеспечивает появление дополнительной поляризации при низкой энергии, т. е. там, где теория в этом нуждается. Однако дополнительная поляризация не принимает участия в процессах при высокой энергии, так что бессмысленные взаимодействия при высокой энергии не возникают.
Рассмотрим теперь конкретную модель спонтанного нарушения симметрии слабого взаимодействия, в которой используется механизм Хиггса. С помощью этого варианта механизма Хиггса мы увидим, каким образом приобретают массу элементарные частицы Стандартной модели.
Механизм Хиггса
В механизме Хиггса фигурирует поле, которое физики называют хиггсовским полем. Как мы видели, поля в квантовой теории поля — это объекты, способные рождать частицы в любой точке пространства. Каждый тип поля порождает свой собственный специфический тип частиц. Например, источником электронов является электронное поле. Аналогично, хиггсовское поле является источником хиггсовских частиц.
Как тяжелые кварки и лептоны, так и хиггсовские частицы настолько массивны, что мы их не обнаруживаем в обычной материи. Однако в противоположность тяжелым кваркам и лептонам, хиггсовские частицы, которые порождаются хиггсовским полем, никто никогда не наблюдал, даже в опытах, осуществленных на ускорителях больших энергий. Это не означает, что хиггсовские частицы не существуют, просто они слишком тяжелы для того, чтобы рождаться при доступных энергиях. Физики ожидают, что если хиггсовская частица существует, мы сможем найти ее всего через несколько лет, когда вступит в строй ускоритель высоких энергий БАК (Большой адронный коллайдер, по англ. LHC, Large Hadron Collider) в Женеве[115].
Тем не менее мы достаточно ясно уверены в том, что механизм Хиггса приложим к нашему миру, так как это единственный известный способ придать массы частицам Стандартной модели. Это единственно известное решение тех проблем, которые мы представили в предыдущей главе. Так как никто пока что не обнаружил хиггсовскую частицу, мы, к сожалению, до сих пор точно не знаем, что такое хиггсовское поле (или поля).
Природа хиггсовской частицы является одним из наиболее горячо обсуждаемых вопросов в физике частиц. В этом разделе я опишу простейшую из многих моделей-кандидатов, содержащих разные частицы и взаимодействия, которая покажет, как работает механизм Хиггса. Какой бы ни оказалась истинная теория хиггсовского поля, она будет включать механизм Хиггса — спонтанное нарушение симметрии слабого взаимодействия и придание масс элементарным частицам в том же духе, что и модель, которую я сейчас опишу.
В этой модели пара полей испытывает слабое взаимодействие. Будет удобно далее считать, что эти два хиггсовских поля, участвующие в слабом взаимодействии, несут заряд слабого взаимодействия. При описании этого механизма часто допускают небрежности в терминологии, так что иногда «хиггс» означает два поля вместе, а иногда — одно из полей (а часто и хиггсовскую частицу, которую мы надеемся найти). Здесь я буду обозначать отдельные поля как хиггс1 и хиггс2
Оба поля хиггс1 и хиггс2 могут рождать частицы, но они могут также принимать ненулевые значения, даже если никаких частиц нет. До этого момента мы не сталкивались с подобными ненулевыми значениями для квантовых полей. До сих пор, помимо электрических и магнитных полей, мы рассматривали только квантовые поля, которые рождают или уничтожают частицы, но принимают нулевые значения в отсутствие частиц. Но квантовые поля могут также иметь ненулевые значения, точно так же, как классические электрические и магнитные поля. Согласно механизму Хиггса, одно из хиггсовских полей принимает ненулевое значение. Мы сейчас покажем, что это ненулевое значение и есть в конечном итоге источник масс частиц.
Самый лучший способ представить себе поле, принимающее ненулевое значение, это думать о нем как о пространстве, где есть заряд поля, но нет реальных частиц. Вы должны думать о заряде, который несет поле, как о присутствующем везде. Увы, это довольно абстрактное понятие, так как само поле есть абстрактный объект. Но когда поле принимает ненулевое значение, последствия вполне конкретны: заряд, который должно нести ненулевое поле, существует в реальном мире.
В частности, ненулевое хиггсовское поле распределяет слабый заряд по всей Вселенной. Происходит это так, как будто ненулевое, несущее слабый заряд хиггсовское поле размазывает этот заряд по всему пространству. Ненулевое значение хиггсовского поля означает, что слабый заряд, который переносит хиггс1 и хиггс2, находится везде, даже там, где нет частиц. Вакуум — состояние Вселенной без частиц — сам несет слабый заряд, когда одно из двух хиггсовских полей принимает ненулевое значение.
Слабые калибровочные бозоны взаимодействуют со слабым зарядом вакуума точно так же, как они взаимодействуют с любыми другими слабыми зарядами. Далее, заряд, заполняющий вакуум, блокирует слабые калибровочные бозоны, когда они пытаются распространить взаимодействия на большие расстояния. Чем дальше они пытаются распространиться, тем больше «краски» встречают на своем пути. (Так как заряд реально распространяется по трем измерениям, вам может показаться более понятной аналогия с пятном из краски.)
Роль хиггсовского поля очень похожа на роль гаишников в истории выше и сводится к ограничению влияния слабого взаимодействия очень малыми расстояниями. При попытке передать слабое взаимодействие удаленным частицам слабые калибровочные бозоны, переносящие взаимодействие, влетают в хиггсовское поле, которое мешает их движению и не пропускает дальше. Подобно Икару, который мог свободно удаляться только на расстояние в полмили, слабые калибровочные бозоны движутся без помех только на очень коротких расстояниях порядка 10-16 см. Слабые калибровочные бозоны и Икар свободно путешествуют на короткие расстояния, но на дальних расстояниях их задерживают.
В вакууме слабый заряд размазан так тонко, что на коротком расстоянии почти не чувствуются следы ненулевого хиггсовского поля и связанного с ним заряда. На коротких расстояниях кварки, лептоны и слабые калибровочные бозоны распространяются свободно, как будто заряд вакуума практически не существует. Поэтому слабые калибровочные бозоны передают взаимодействия на короткие расстояния, как будто оба хиггсовских поля равны нулю.
Однако на больших расстояниях частицы разлетаются все дальше и поэтому испытывают более значительное влияние слабого заряда. Конкретное количество этого заряда зависит от плотности заряда, которая, в свою очередь, зависит от величины ненулевого хиггсовского поля. Путешествие на большие расстояния (и передача слабого взаимодействия) не есть вопрос выбора для слабых калибровочных бозонов низких энергий, так как во время экскурсий на большие расстояния слабый заряд в вакууме накапливается по дороге.
Именно это требуется нам для того, чтобы придать смысл существованию слабых калибровочных бозонов. Квантовая теория поля утверждает, что частицы, которые свободно движутся на короткие расстояния, и только необычайно редко — на большие расстояния, обладают ненулевой массой. Прерванное путешествие слабых калибровочных бозонов означает, что они ведут себя так, как будто обладают массой, так как именно массивные калибровочные бозоны далеко не улетают. Пропитывающий пространство слабый заряд препятствует путешествию слабых калибровочных бозонов, заставляя их вести себя в точности так, как это необходимо для согласия с экспериментами.
Плотность слабых зарядов в вакууме примерно соответствует числу зарядов, находящихся на расстоянии 10-16 см. При такой плотности слабого заряда массы слабых калибровочных бозонов — заряженных W± и нейтрального Z0 — принимают измеренные значения, равные примерно 100 ГэВ.
И это не все, на что способен механизм Хиггса. Он также несет ответственность за массы кварков и лептонов — элементарных частиц, образующих вещество в Стандартной модели. Кварки и лептоны приобретают массу способом, очень похожим на тот, который используется для слабых калибровочных бозонов. Кварки и лептоны взаимодействуют с распределенным в пространстве хиггсовским полем, и поэтому испытывают сопротивление со стороны слабого заряда Вселенной. Как и слабые калибровочные бозоны, кварки и лептоны приобретают массу за счет отскоков от хиггсовкого заряда, распределенного во всем пространстве-времени. Если бы не было хиггсовского поля, эти частицы должны были бы иметь нулевую массу. Но повторим еще раз: ненулевое хиггсовское поле и слабый заряд вакуума препятствуют движению и заставляют частицы иметь массу. Чтобы приобрести свою массу, кваркам и лептонам также необходим механизм Хиггса.
Может создаться впечатление, что механизм Хиггса является избыточно хитроумным способом приобретения массы, чем это необходимо, но квантовая теория поля говорит, что это есть единственный разумный способ приобретения массы слабыми калибровочными бозонами. Красота механизма Хиггса состоит в том, что он придает массу слабым калибровочным бозонам, осуществляя именно ту задачу, которая была поставлена в начале этой главы. Механизм Хиггса выглядит так, как будто симметрия слабого взаимодействия сохраняется на малых расстояниях (что, согласно квантовой механике и специальной теории относительности, эквивалентно высоким энергиям), но нарушается на больших расстояниях (что эквивалентно низким энергиям). Механизм Хиггса нарушает симметрию слабого взаимодействия спонтанно, и это спонтанное нарушение лежит в основе решения проблемы массивных калибровочных бозонов. Этот более сложный вопрос объясняется в следующем разделе (при желании вы можете пропустить его и перейти сразу к следующей главе).
Спонтанное нарушение симметрии слабого взаимодействия
Мы видели, что связанное со слабым взаимодействием преобразование внутренней симметрии меняет местами все, что обладает зарядом слабого взаимодействия, так как преобразование симметрии действует на все, что взаимодействует со слабыми калибровочными бозонами. Следовательно, такая внутренняя симметрия должна действовать и на поля хиггс1 и хиггс2, или, иначе говоря, на частицы хиггс1 и хиггс2, которые эти поля порождают, и также рассматривать их как эквивалентные. Аналогично рассматриваются как взаимозаменяемые частицы кварки и и d, также испытывающие слабое взаимодействие.
Если бы оба хиггсовских поля были равны нулю, они были бы эквивалентны и взаимозаменяемы, так что полная симметрия, связанная со слабым взаимодействием, должна была бы сохраняться. Однако, когда одно из двух хиггсовских полей принимает ненулевое значение, хиггсовские поля спонтанно нарушают симметрию слабого взаимодействия. Если одно из полей равно нулю, а другое — нет, то нарушается электрослабая симметрия, благодаря которой хиггс1 и хиггс2 взаимозаменяемы.
Точно так же, как первый гость, выбравший себе левый или правый стакан, нарушает лево-правую симметрию за круглым столом, одно хиггсовское поле, принявшее ненулевое значение, нарушает симметрию слабого взаимодействия, обменивающую два хиггсовских поля. Симметрия нарушается спонтанно, так как то, что ее нарушает, это вакуум — реальное состояние системы, в данном случае, ненулевое поле. Тем не менее законы физики, остающиеся неизменными, сохраняют симметрию.
С помощью картинки можно проследить, каким образом ненулевое поле нарушает симметрию слабого взаимодействия. На рис. 58 показан график с двумя осями, помеченными х и у. Эквивалентность двух хиггсовских полей похожа на эквивалентность осей х и у, на которых не помечены точки. Если повернуть график так, чтобы оси поменялись местами, картинка будет выглядеть так же, как и раньше. Это есть следствие обычной вращательной симметрии.

Заметим, что если изобразить точку в положении х = 0, у = 0, то вращательная симметрия полностью сохранится. Но если изобразить точку так, что у нее появится одна ненулевая координата, например, если x = 5 и y = 0, то вращательная симметрия оказывается нарушенной. Две оси уже более не эквивалентны, так как у этой точки значение ж, но не у, отлично от нуля.
Аналогичным образом механизм Хиггса спонтанно нарушает симметрию слабого взаимодействия. Если два хиггсовских поля равны нулю, симметрия сохраняется. Но если одно поле равно нулю, а другое отлично от нуля, симметрия слабого взаимодействия спонтанно нарушается.
Массы слабых калибровочных бозонов характеризуют точную величину энергии, при которой спонтанно нарушается симметрия слабого взаимодействия. Эта энергия равна 250 ГэВ, так что масштаб энергии слабых взаимодействий очень близок к массам слабых калибровочных бозонов W-, W+ и Z. Когда энергия частиц больше 250 ГэВ, взаимодействия происходят так, как будто симметрия сохраняется, но если энергия частиц меньше 250 ГэВ, симметрия нарушена и слабые калибровочные бозоны взаимодействуют так, как будто у них есть масса. При правильно подобранном значении неисчезающего хиггсовского поля симметрия слабого взаимодействия спонтанно нарушается при нужной энергии, а слабые калибровочные бозоны получают в точности нужную массу.
Преобразования симметрии, действующие на слабые калибровочные бозоны, действуют также на кварки и лептоны. При этом оказывается, что такие преобразования не будут оставлять все неизменным, за исключением случая, когда кварки и лептоны безмассовы. Это означает, что симметрия слабого взаимодействия будет сохраняться, только если кварки и лептоны не будут иметь массы. Так как симметрия слабого взаимодействия существенна при больших энергиях, то спонтанное нарушение симметрии необходимо не только для того, чтобы массы появились у слабых калибровочных бозонов, но и для того, чтобы массу приобрели кварки и лептоны. Механизм Хиггса — единственный способ приобретения масс у всех массивных фундаментальных частиц Стандартной модели.
Механизм Хиггса действует именно так, как требуется для того, чтобы в любой теории, включающей этот механизм, могли появиться массивные слабые калибровочные бозоны (а также массивные кварки и лептоны), но тем не менее можно было получать правильные предсказания для поведения процессов при больших энергиях. В частности, для слабых калибровочных бозонов больших энергий (т. е. с энергией больше 250 ГэВ) симметрия, по-видимому, сохраняется, так что неправильных предсказаний не возникает. При больших энергиях внутренняя симметрия, связанная со слабым взаимодействием, отсекает проблематичную поляризацию слабого калибровочного бозона, которая могла бы привести к слишком большой вероятности взаимодействий. Но при низких энергиях, когда масса существенна, чтобы согласовать с опытом короткий радиус слабых взаимодействий, эта симметрия нарушается.
Именно поэтому механизм Хиггса столь важен. Ни одна другая теория, содержащая такие массы, не обладает указанными свойствами. Другие идеи проваливаются либо при низких энергиях, когда приводят к неправильным массам, либо при высоких энергиях, где неправильно предсказываются вероятности взаимодействий.
Бонус
Существует еще одно интересное свойство Стандартной модели, которое я еще не объяснила. Хотя в последующих главах будет идти речь о хиггсовском поле, это свойство нам не понадобится, поэтому обсуждаться не будет. Однако оно настолько удивительное, что его нельзя не упомянуть.
Механизм Хиггса говорит нам не только о слабом взаимодействии. Удивительным образом он позволяет глубже понять, почему электромагнетизм является особенным взаимодействием. До 1960-х годов никто не верил, что можно узнать что-то новое об электромагнитном взаимодействии, которое усиленно и успешно изучалось на протяжении почти ста лет. Однако в 1960-е годы предложенная Шелдоном Глэшоу, Стивеном Вайнбергом и Абдусом Саламом электрослабая теория предсказала, что когда Вселенная начала свою эволюцию при высоких температуре и энергии, существовали три слабых калибровочных бозона и четвертый, независимый нейтральный бозон, отвечающий за другую силу взаимодействия. Вездесущий и важный в наши дни фотон не входил в этот список. Авторы электрослабой теории вывели свойства четырех слабых калибровочных бозонов на основании как математических, так и физических аргументов, которые я здесь не буду обсуждать.
Примечательно, что фотон изначально ничем не выделялся. А на самом деле фотон, о котором мы говорим сегодня, есть смесь двух из четырех исходных калибровочных бозонов. Причина особого положения фотона состоит в том, что он — единственный калибровочный бозон, участвующий в электрослабых взаимодействиях, который не подвержен влиянию слабого заряда вакуума. Главным отличительным свойством фотона является то, что он может без помех путешествовать сквозь слабо заряженный вакуум, и поэтому сам не имеет массы.
В противоположность W и Z, движение фотона не нарушается ненулевым зарядом хиггсовского поля. Это происходит потому, что, несмотря на наличие у вакуума слабого заряда, у него нет электрического заряда. Фотон, переносящий электромагнитное взаимодействие, взаимодействует только с электрически заряженными телами. По этой причине фотон может переносить дальнодействующее взаимодействие без всяких помех со стороны вакуума. Поэтому фотон остается единственным безмассовым калибровочным бозоном, даже при наличии ненулевого хиггсовского ПОЛЯ.
Ситуация очень напоминает радарные ловушки для лихачей, с которыми вступил в борьбу Икар (хотя, по общему признанию, эта часть аналогии несколько слабее). Ловушки для лихачей пропускают скучные автомобили безнаказанно. Фотоны, как скучные нейтральные автомобили, всегда распространяются без помех.
Кто бы мог подумать? Фотон, про который физики в течение многих лет считали, что знают про него все, имеет происхождение, которое можно понять только в рамках более сложной теории, объединяющей слабое и электромагнитное взаимодействия в единую теорию. Эту теорию принято называть электрослабой теорией, а соответствующую симметрию — электрослабой симметрией. Электрослабая теория и механизм Хиггса — главные успехи физики частиц. В рамках этой теории ясно объясняются не только массы слабых калибровочных бозонов, но и значение фотона. Кроме того, теория позволяет понять происхождение масс кварков и лептонов. Только что рассмотренные нами довольно абстрактные идеи четко объясняют весьма широкий круг свойств нашего мира.
Предупреждение
Механизм Хиггса действует замечательно и придает массы кваркам, лептонам и слабым калибровочным бозонам, не приводя при этом к бессмысленным предсказаниям при высоких энергиях, а также объясняет, откуда возник фотон. Однако осталось еще одно существенное свойство хиггсовской частицы, которое физики до конца не понимают.
Для того чтобы придать частицам их измеряемые массы, электрослабая симметрия должна быть нарушена примерно при 250 ГэВ. Эксперименты показывают, что частицы с энергиями больше 250 ГэВ ведут себя так, как будто они безмассовы, в то время как частицы с энергиями меньше 250 ГэВ действуют так, как будто у них есть массы. Однако электрослабая симметрия будет нарушаться при энергиях порядка 250 ГэВ, только если хиггсовская частица (иногда ее называют хиггсовским бозоном) сама имеет примерно такую же массу (мы опять используем соотношение E = mc2). Теория слабого взаимодействия не будет работать, если масса хиггсовского бозона будет намного больше. Если бы масса хиггсовского бозона была больше, нарушение симметрии происходило бы при более высокой энергии, и слабые калибровочные бозоны были бы тяжелее, в противоречии с экспериментальными данными.
Однако ниже, в гл. 12, мы увидим, что легкая хиггсовская частица приводит к большой теоретической проблеме. Вычисления с учетом квантовой механики говорят, что хиггсовская частица должна быть гораздо тяжелее, и физики до сих пор не понимают, почему масса хиггсовского бозона должна быть столь малой. Это затруднение стимулирует ученых к обсуждению новых идей в физике частиц и построению ряда моделей с дополнительным числом измерений, которые мы позднее рассмотрим.
Даже до конца не понимая точную природу хиггсовской частицы и причину, по которой она столь легка, мы видим из требования на массу, что Большой адронный коллайдер (БАК), который приступит к работе в ближайшее время в ЦЕРНе (Швейцария), должен открыть одну или несколько критически важных новых частиц. Что бы ни нарушало электрослабую симметрию, оно должно иметь массу в окрестности масштаба массы слабых взаимодействий. И мы ожидаем, что БАК обнаружит, что это такое. Если это критически важное открытие случится, оно позволит глубоко продвинуться вперед в понимании лежащей в основе строения мира структуры материи. И это укажет нам, какое из предложений (если мы до него догадались) по объяснению хиггсовской частицы правильно.
Однако, прежде чем мы перейдем к этим предложениям, нам следует рассмотреть одно возможное расширение Стандартной модели, которое было предложено исключительно в интересах простоты описания природы. В следующей главе рассматриваются виртуальные частицы, зависимость взаимодействий от расстояния и заманчивый вопрос о великом объединении.
Что стоит запомнить
• Несмотря на важность симметрий для формулировки правильных предсказаний о поведении частиц при высоких энергиях, массы кварков, лептонов и слабых калибровочных бозонов указывают на то, что симметрия слабого взаимодействия должна быть нарушена.
• Поскольку мы должны избавиться от неверных предсказаний, симметрия слабого взаимодействия должна, тем не менее, сохраняться при высоких энергиях. Следовательно, симметрия слабого взаимодействия должна нарушаться только при низких энергиях.
• Когда во всех физических законах симметрия сохраняется, а в конкретной физической системе не сохраняется, то возникает спонтанное нарушение симметрии. Спонтанно нарушенные симметрии — это симметрии, которые сохраняются при высоких энергиях и нарушаются при низких энергиях. Симметрия слабого взаимодействия спонтанно нарушена.
• Процесс, с помощью которого происходит спонтанное нарушение симметрии слабого взаимодействия, называется механизмом Хиггса. Для этого должна существовать частица с массой порядка масштаба массы слабых взаимодействий, равной 250 ГэВ (напомним, что специальная теория относительности связывает энергию и массу соотношением E = mc2).
Глава 11
Скейлинг и Великое объединение: связь взаимодействий на разных расстояниях и при разных энергиях
I hope someday you’ll join us
And the world will live as one.
John Lennon[116]
Афине часто казалось, что интересные новости доходили до нее в последнюю очередь. Она ничего не слышала о приключениях Икара с автомобилем, пока не прошло больше месяца со дня его покупки. И узнала-mo она об этих приключениях совсем не от него, а от своей подруги, которая слышала о них от брата кузена Дитера, а он узнал о них от кузена Дитера, который слышал о них от самого Дитера.
Таким окольным путем до Афины дошла следующая фраза, сказанная Икаром: «Интенсивность силы зависит от места, где вы были». Эти странные слова, совсем не характерные для Икара, сначала сбили Афину с толку, но потом она поняла, что фраза по дороге исказилась, как в испорченном телефоне. После некоторых раздумий она решила, что на самом деле замечание Икара было таким: «Эффективность машины зависит от модели автомобиля»[117].
Мы увидим, что первоначально услышанное Афиной замечание правильно. В этой главе рассказывается о том, как физические процессы, происходящие между частицами, находящимися на одном расстоянии друг от друга, могут быть связаны с процессами, происходящими между частицами, находящимися на другом расстоянии, и почему физические величины, например масса частицы или константа взаимодействия, зависят от энергии частицы. Эта зависимость от энергии и расстояния превосходит классическую зависимость сил от расстояния. Например, с классической точки зрения, напряженность электромагнитного, а также гравитационного полей уменьшается обратно пропорционально квадрату расстояния между взаимодействующими телами (закон обратных квадратов). Но квантовая механика изменяет эту зависимость от расстояния, оказывая влияние на напряженность самого взаимодействия, так что частицы на разных расстояниях (и при разных энергиях) взаимодействуют как бы с разными зарядами.
С увеличением расстояния взаимодействия становятся слабее или сильнее за счет виртуальных частиц — короткоживущих частиц, существующих как следствие законов квантовой механики и соотношения неопределенностей. Виртуальные частицы взаимодействуют с калибровочными бозонами и изменяют взаимодействия так, что они становятся зависящими от расстояния, что напоминает то, как друзья Афины исказили слова Икара, передавая их от одного к другому.
Квантовая теория поля показывает, как вычислить влияние виртуальных частиц на зависимость взаимодействий от расстояния и энергии. Одним из триумфов подобных вычислений было объяснение того, почему сильное взаимодействие так сильно. Другим интересным следствием стала потенциальная возможность существования теории Великого объединения (ТВО), в рамках которой столь различные при низких энергиях три негравитационных взаимодействия сливаются в единое взаимодействие при высоких энергиях. Мы воспользуемся ниже этими результатами и теми идеями и вычислениями в квантовой теории поля, которые к ним приводят.
В следующих главах следует иметь в виду насколько сильно различаются масштабы энергий, которые мы обсуждаем. Энергия объединения составляет одну тысячу триллионов ГэВ, а планковский масштаб энергии, на котором гравитация становится сильной, еще примерно в тысячу раз больше. Энергетический масштаб слабых взаимодействий, равный энергии, при которой осуществляются современные эксперименты, неизмеримо меньше; он находится в пределах от ста до тысячи ГэВ. Слабый масштаб энергий настолько же мал по сравнению с энергией Великого объединения, насколько размер мраморного шарика мал по сравнению с расстоянием от Земли до Солнца. Поэтому иногда я буду называть масштаб слабых взаимодействий низкоэнергетическим, несмотря на то что это очень большая энергия с точки зрения экспериментальных перспектив, но в то же время она намного меньше энергетического масштаба Великого объединения и планковского масштаба.
Крупным и мелким планом
Эффективные теории поля используют идею эффективной теории, о которой шла речь в гл. 1, в приложении к квантовой теории поля. Они концентрируют внимание на тех масштабах энергии и расстояния, которые есть надежда измерить. Эффективная теория поля, примененная на определенном масштабе энергии и расстояния, «эффективно» описывает те энергии и расстояния, которые нас интересуют. Эта теория фокусируется на тех силах и взаимодействиях, которые могут проявиться, когда энергия частиц[118] не превосходит некоторой заданной величины, и пренебрегает энергиями, которые недостижимо выше. Теория не занимается деталями физических процессов и поведения частиц, которые происходят при энергиях, много больших тех, которые можно достичь.
Одно из преимуществ эффективной теории поля состоит в том, что даже если вы не знаете, какие взаимодействия имеют место на коротких расстояниях, вы можете продолжать изучение величин, существенных на интересующих вас масштабах. Вам нужно всего лишь думать о величинах, которые вы можете (в принципе) измерить. Когда вы смешиваете краски, вам не нужно знать их подробную молекулярную структуру. Но, скорее всего, вас интересуют непосредственно воспринимаемые свойства, такие как цвет и текстура. Имея эту информацию, и даже не зная микроструктуру вашей краски, вы можете расклассифицировать краски по их свойствам и предсказать, как будет выглядеть смесь красок, когда вы перенесете их на холст.
Однако, если вам известен химический состав ваших красок, правила физики позволяют установить некоторые их свойства. Эта информация не нужна вам, когда вы рисуете (используете эффективную теорию), но она может оказаться полезной, когда вы смешиваете краски (выводите параметры эффективной теории из более фундаментальной теории).
Аналогично, если вы не знаете, как выглядит теория на малых расстояниях (при больших энергиях), вам не удастся вывести измеримые величины. Однако, если вы знаете детали поведения на малых расстояниях, квантовая теория поля точно указывает, как связаны разные эффективные теории, применяемые при разных энергиях. Квантовая теория поля позволяет вам вывести величины, относящиеся к одной эффективной теории, например, массы или константы взаимодействия, зная величины, относящиеся к другой эффективной теории.
Метод вычисления зависимости наблюдаемых величин от энергии или расстояния, впервые развитый в 1974 году Кеннетом Вильсоном, получил причудливое название ренормализационной группы. Наряду с симметриями, двумя другими самыми мощными инструментами исследования в физике являются методы эффективной теории и ренормализационной группы, причем оба эти метода включают рассмотрение физических процессов на очень разных масштабах расстояний или энергий. Слово «группа» пришло в эту теорию из математики, хотя его математическое происхождение для нас несущественно.
Слово ренормализация звучит получше. Имеется в виду тот факт, что на каждом интересующем нас масштабе расстояний вы делаете паузу, чтобы решить, что делать дальше. Вы определяете, какие частицы и взаимодействия существенны при определенных интересующих вас в данный момент энергиях. Затем вы совершаете новую нормировку, т. е. новую калибровку каждого параметра теории.
Метод ренормализационной группы использует идеи, напоминающие те, которые были описаны в гл. 2. Там мы обсуждали возможность интерпретации теории более высокой размерности на языке теории меньшей размерности и исследовали двумерную теорию с одним малым свернутым измерением, как будто теория была только одномерной. Сворачивая измерения, мы игнорировали все детали того, что происходило внутри лишних измерений, и предполагали, что все можно описать с помощью меньшего числа измерений. Новой «нормировкой» было четырехмерное описание, которое можно было использовать, если сосредоточиться на изучении больших расстояний.
Очень похожую процедуру можно использовать для построении теории, применимой на больших расстояниях, исходя из теории, работающей на малых расстояниях. Для этого решите, какая минимальная длина вас интересует, и «сотрите» физику, относящуюся к меньшим расстояниям. Один из способов сделать это — взять средние значение тех величин, чьи детали поведения могут отличаться только на меньших расстояниях, которыми мы решили пренебречь. Допустим, вы смотрите на решетку, заполненную серыми точками разных оттенков. Тогда, вы буквально усредняете оттенки более мелких точек, чтобы определить тот оттенок более крупных точек, который будет воспроизводить цветовой эффект.
Ваши глаза делают это автоматически, когда вы смотрите на какое-то размытое изображение.
Если вы способны видеть предметы только с заданным уровнем точности и хотите делать полезные вычисления, связывающие измеримые величины, то вам не требуется знать, что происходит на меньших масштабах. Самый эффективный подход часто включает выбор «размера пикселя» в вашей теории, согласующийся с вашим уровнем точности. Таким путем вы можете, например, пренебречь тяжелыми частицами, которые вы никогда не сможете породить, и короткодействующими взаимодействиями, которые никогда не случаются. Вместо этого вы можете сконцентрировать ваши вычисления на частицах и взаимодействиях, относящихся к той энергии, которую удается достичь.
Однако, если вы знаете более точную теорию, применимую на меньших расстояниях, ее можно использовать для расчета параметров интересующей вас эффективной теории, т. е. эффективной теории с меньшим разрешением. Так же как в примере с серыми точками разных оттенков, когда вы переходите от эффективной теории с короткодействующим разрешением к другой теории с менее точным разрешением, вы по существу меняете «размер пикселя», который вы выбрали для анализа вашей теории. Метод ренормализационной группы говорит вам, как вычислить то влияние, которое могут иметь такие короткодействующие взаимодействия на частицы в вашей дальнодействующей теории. Вы экстраполируете физические процессы от одного масштаба длины или энергии к другому.
Виртуальные частицы
Вычисления по методу ренормализационной группы осуществляют эти экстраполяции, учитывая влияние квантово-механических процессов и виртуальных частиц. Виртуальные частицы, являющиеся следствием квантовой механики, — странные, призрачные двойники реальных частиц. Они внезапно возникают и исчезают, существуя в реальности лишь крохотный промежуток времени. Виртуальные частицы подвержены тем же взаимодействиям и обладают теми же зарядами, что и физические частицы, но их энергии кажутся неправильными. Например, очевидно, что движущаяся очень быстро частица обладает запасом энергии. В то же время виртуальная частица может обладать колоссальной скоростью и не иметь энергии. На самом деле виртуальная частица может иметь любую энергию, отличающуюся от энергии, которую имеет соответствующая реальная физическая частица. Если бы она имела такую же энергию, она была бы не виртуальной, а реальной частицей. Существование виртуальных частиц — странное свойство квантовой теории поля, которое следует учитывать, чтобы делать правильные предсказания.
Так как же могут существовать эти кажущиеся невозможными частицы? Виртуальная частица с ее взятой взаймы энергией не могла бы существовать, если бы не соотношение неопределенностей, позволяющее частицам иметь неправильную энергию в течение промежутка времени, настолько короткого, что его никогда нельзя измерить.
Соотношение неопределенностей утверждает, что измерение энергии (или массы) с бесконечной точностью потребовало бы бесконечно долгого времени, и чем дольше живет частица, тем точнее можно осуществить измерение ее энергии. Однако, если частица короткоживущая и ее энергию никак невозможно определить с бесконечной точностью, то энергия может на время отклониться от значения, которым обладает истинная долгоживущая частица. На самом деле, в силу соотношения неопределенностей, частицы будут делать все, что им захочется, так долго, как могут. У виртуальных частиц нет угрызений совести, и они плохо ведут себя всякий раз, когда никто не видит. (Один физик из Амстердама даже предположил, что эти частицы голландцы.)
Вакуум можно представлять себе как резервуар энергии. Виртуальные частицы — это частицы, возникающие из вакуума и на время одалживающие у него часть энергии. Они существуют только одно мгновение, а затем возвращаются обратно в вакуум, унося с собой энергию, которую одолжили. Эта энергия может вернуться на свое первоначальное место, или может быть передана частицам, находящимся в другом месте.
Квантово-механический вакуум — беспокойное место. И хотя вакуум по определению пуст, квантовые эффекты приводят к тому, что он кишит виртуальными частицами и античастицами, которые рождаются и уничтожаются, даже несмотря на то, что стабильные долгоживущие частицы отсутствуют. В принципе могут рождаться любые пары частиц и античастиц, но на очень короткое время, что не позволяет их непосредственно наблюдать. Однако каким бы кратким ни было их существование, мы должны учитывать виртуальные частицы, так как несмотря ни на что они оставляют свои отпечатки на взаимодействиях долгоживущих частиц.
Наличие виртуальных частиц приводит к измеряемым следствиям, так как они влияют на взаимодействия реальных физических частиц, входящих в область взаимодействия и покидающих ее. За краткое время своего существования виртуальная частица может пролететь от одной реальной частицы к другой, прежде чем исчезнуть и вернуть свой энергетический долг вакууму. Таким образом, виртуальные частицы выступают в качестве посредников, влияющих на взаимодействия долгоживущих стабильных частиц.
Например, фотон на рис. 47 (стр. 137), обмен которым порождал классическое электромагнитное взаимодействие, был на самом деле виртуальным фотоном. Его энергия не равнялась энергии реального фотона, но этого и не требовалось. Нужно было всего лишь, чтобы он существовал достаточно долго, чтобы передать электромагнитное взаимодействие и позволить взаимодействовать реальным заряженным частицам.
Другой пример виртуальных частиц показан на рис. 59. Здесь фотон влетает в область взаимодействия, рождается виртуальная электрон-позитронная пара, а затем эта пара поглощается в другом месте. В том месте, где частицы поглощаются, из вакуума возникает другой фотон, который уносит энергию, временно одолженную промежуточной электрон-позитронной парой. Исследуем одно примечательное свойство взаимодействия этого типа.
Почему интенсивность взаимодействия зависит от расстояния?
Интенсивность известных нам взаимодействий зависит от энергий участвующих во взаимодействиях частиц и расстояний между ними, и частично эта зависимость определяется виртуальными частицами. Например, интенсивность электромагнитного взаимодействия меньше, когда два электрона удалены на большее расстояние друг от друга. (Напомним, что это квантово-механическое уменьшение существует дополнительно к классической зависимости электромагнетизма от расстояния.) Следствия, к которым приводят виртуальные частицы и зависимость взаимодействий от расстояния, вполне реальны; теоретические предсказания и эксперименты очень хорошо согласуются друг с другом.
Причина того, что параметры эффективной теории, например интенсивность взаимодействий, зависят от энергий и расстояния между участвующими частицами, вытекает из свойства квантовой теории поля, которое физик Джонатан Флинн шутливо назвал анархическим принципом [119]. Этот принцип следует из квантовой механики, которая утверждает, что все взаимодействия частиц, которые могут случиться, случаются. В квантовой теории поля все, что не запрещено, произойдет.
Назовем путем каждый отдельный процесс, в котором участвует конкретная группа физических частиц. Путь может как включать, так и не включать виртуальные частицы. Если верно первое, будем называть путь квантовым вкладом. Квантовая механика утверждает, что в результирующую интенсивность взаимодействия вносят вклад все возможные пути. Например, физические частицы могут превращаться в виртуальные частицы, которые, в свою очередь, могут взаимодействовать друг с другом и затем превращаться в другие физические частицы. В таком процессе могут вновь возникнуть первоначальные физические частицы или эти частицы могут превратиться в другие физические частицы. И хотя виртуальные частицы не могут долго существовать, что не позволяет нам непосредственно их наблюдать, они влияют на то, как реальные наблюдаемые частицы взаимодействуют друг с другом.
Попытку уберечь виртуальные частицы от участия во взаимодействии можно сравнить с такой ситуацией: допустим, вы поделились секретом с одним вашим приятелем и надеетесь, что этот секрет не достигнет ушей другого вашего приятеля. Вы знаете, что рано или поздно кто-нибудь из «промежуточных виртуальных» приятелей выдаст ваш секрет и расскажет его этому другому приятелю. Даже если вы уже сами рассказали ему, в чем дело, сам факт, что ваши виртуальные приятели обсуждали с ним ваш секрет, будет влиять на его мнение о предмете. На самом деле его мнение будет суммой мнений всех, с кем он разговаривал.
В передаче взаимодействий между физическими частицами играют роль не только прямые взаимодействия между ними, но и непрямые взаимодействия, содержащие виртуальные частицы. Точно так же, как на мнение вашего приятеля оказывают влияние мнения всех разговаривавших с ним, окончательное взаимодействие между частицами есть сумма всех возможных вкладов, включая вклады от виртуальных частиц. Поскольку важность вклада виртуальных частиц зависит от расстояний, интенсивность взаимодействий также зависит от расстояния.
Метод ренормализационной группы дает точные указания, как вычислить вклад виртуальных частиц в любое взаимодействие. Все вклады промежуточных виртуальных частиц суммируются, и это либо усиливает, либо ослабляет интенсивность взаимодействий калибровочных бозонов.
Непрямые взаимодействия играют более важную роль, когда взаимодействующие частицы находятся дальше друг от друга. Большее расстояние аналогично тому, что вы рассказываете свой секрет большему числу «виртуальных» приятелей. Хотя вы не можете быть уверены в том, что каждый отдельный приятель выдаст ваш секрет, но чем большему количеству приятелей вы расскажете его, тем больше вероятность, что кто-то «проколется». Всякий раз, когда существует путь, по которому виртуальные частицы могут дать вклад в полную интенсивность взаимодействия, квантовая механика гарантирует, что это произойдет. При этом величина влияния виртуальных частиц на интенсивность взаимодействия зависит от расстояния, на которое распространяется сила взаимодействия.
Однако реальные вычисления по методу ренормализационной группы еще умнее, так как они также суммируют вклады бесед приятелей друг с другом. Более ясная аналогия со вкладами за счет виртуальных частиц напоминает пути документа, проходящего сквозь большое бюрократическое учреждение. Если человек, находящийся на вершине иерархии, посылает письмо, оно немедленно проходит сквозь учреждение. Но послания кого-то, находящегося на более низком уровне иерархии, будут подвергнуты проверке его начальниками. Если письмо исходит от кого-то, находящегося на еще более низком уровне, оно сначала может быть втянуто в бюрократическую машину и пройти все ее уровни, прежде чем в конце концов достигнет места назначения. В этом случае бюрократы на каждом уровне будут рассылать документ всем работникам своего уровня, прежде чем послать его последовательно на более высокий уровень. Только достигнув верхних эшелонов, документ будет выпущен из учреждения. То послание, которое возникнет в этом случае, будет, вообще говоря, не совпадать с оригиналом, а представлять собой документ, многократно профильтрованный многоэтажной бюрократической машиной.
Если представить себе виртуальные частицы как чиновников, причем чиновник верхнего уровня соответствует виртуальной частице большей энергии, то письмо с высокого уровня будет немедленно передано адресату, а документы с более низких уровней должны будут пройти много стадий. Квантово-механический вакуум — это «бюрократическое учреждение», с которым сталкивается фотон. Каждое взаимодействие изучается промежуточными виртуальными частицами со все меньшей энергией. Как и в бюрократической системе, возможны отклонения на всех уровнях (или расстояниях). Некоторые пути будут обходить бюрократические препоны, создаваемые виртуальными частицами, другие будут включать виртуальные частицы, путешествующие на все более далекие расстояния. Передача информации на все меньшие расстояния (все большие энергии) сталкивается со все меньшим количеством виртуальных процессов по сравнению с теми, которые встречаются на больших расстояниях.

Однако между виртуальными процессами и бюрократическим учреждением имеется существенное различие. В бюрократическом учреждении каждое конкретное послание проходит по своему пути, независимо от того, насколько он сложен. С другой стороны, квантовая механика утверждает, что может существовать много путей. При этом она настаивает на том, что средняя интенсивность взаимодействия равна сумме вкладов от всех возможных путей, которые только могут существовать.
Рассмотрим фотон, распространяющийся от одной заряженной частицы к другой. Так как он может по дороге превращаться в виртуальные электрон-позитронные пары (см. рис. 60), квантовая механика утверждает, что когда-то это произойдет. При этом пути с виртуальными электронами и позитронами влияют на эффективность, с которой фотон переносит электромагнитное взаимодействие.
И это не единственный квантово-механический процесс, который может возникнуть. Виртуальные электроны и позитроны могут сами испускать фотоны, которые, в свою очередь, могут превращаться в другие виртуальные частицы и т. д. Расстояние между двумя заряженными частицами, обменивающимися фотоном, определяет число таких взаимодействий, которые произойдут между фотоном-переносчиком и частицами в вакууме, и то, насколько сильным будет это взаимодействие. Интенсивность электромагнитного взаимодействия — это суммарный вклад многих путей, по которым движется фотон, если принять во внимание все возможные бюрократические окольные пути, т. е. квантово-механические процессы с участием виртуальных частиц на больших или малых расстояниях. Так как число виртуальных частиц, с которыми сталкивается фотон, зависит от проходимого им расстояния, интенсивность взаимодействия фотона зависит от расстояния между заряженными телами, с которыми он взаимодействует.
Как показывают вычисления, если сложить все вклады от всех возможных путей, то вакуум ослабляет тот сигнал, который фотон переносит от электрона.
Интуитивное объяснение ослабления электромагнитного взаимодействия состоит в том, что заряды противоположного знака притягиваются, а заряды одного знака отталкиваются, поэтому в среднем виртуальные позитроны находятся ближе к электрону, чем виртуальные электроны. Поэтому заряды от виртуальных частиц ослабляют полное воздействие исходной электрической силы, создаваемой электроном. Квантово-механические эффекты экранируют электрический заряд. Экранировка электрического заряда означает, что интенсивность взаимодействия между фотоном и электроном уменьшается с расстоянием.
Реальная электрическая сила на больших расстояниях оказывается меньше, чем классическая электрическая сила на малых расстояниях, так как фотон, переносящий взаимодействие на короткие расстояния, чаще выбирает путь, не содержащий виртуальных частиц. Фотону, путешествующему на малое расстояние, не требуется проходить сквозь большое ослабевающее облако виртуальных частиц, как это приходится делать фотону, переносящему взаимодействие на большие расстояния.
Не только фотон, но и все переносящие взаимодействие калибровочные бозоны взаимодействуют по дороге к месту назначения с виртуальными частицами. Пары виртуальных частиц — частица и ее античастица — спонтанно извергаются из вакуума и поглощаются им, что влияет на конечную интенсивность взаимодействия. Эти виртуальные частицы на время устраивают засаду на переносящий взаимодействие калибровочный бозон, изменяя суммарную интенсивность взаимодействия. Вычисления показывают, что, как и в случае электромагнитного взаимодействия, интенсивность слабого взаимодействия уменьшается с расстоянием.
Однако виртуальные частицы не всегда навешивают тормоза на взаимодействия. Как это ни удивительно, иногда они могут помочь усилить их. В начале 1970-х годов Дэвид Политцер, который был тогда аспирантом Сидни Коулмена в Гарварде (который и предложил Политцеру задачу), и независимо Дэвид Гросс и его студент Фрэнк Вильчек (оба из Принстона), и, наконец, Герард ’т Хоофт из Голландии проделали вычисления, показавшие, что сильное взаимодействие ведет себя полностью противоположным образом по сравнению с электромагнитным взаимодействием. Вместо экранирования сильного взаимодействия на больших расстояниях и тем самым его ослабления, виртуальные частицы на самом деле усиливают взаимодействия глюонов (частиц, переносящих сильное взаимодействие), так что сильное взаимодействие на больших расстояниях оправдывает свое название. Гросс, Политцер и Вильчек получили Нобелевскую премию по физике 2004 года за глубокое проникновение в суть сильного взаимодействия.
Ключ к этому явлению — поведение самих глюонов. Большое различие между глюонами и фотонами заключается в том, что глюоны взаимодействуют друг с другом. Глюон может влететь в область взаимодействия и превратиться в пару виртуальных глюонов, которые будут оказывать влияние на интенсивность взаимодействия. Эти виртуальные глюоны, как и все виртуальные частицы, существуют только краткий миг. Но их влияние накапливается с ростом расстояния, пока сильное взаимодействие не становится действительно необычайно сильным. Результат вычислений показывает, что виртуальные глюоны чрезвычайно усиливают интенсивность сильного взаимодействия, когда расстояния между частицами растут. Сильное взаимодействие намного сильнее тогда, когда частицы достаточно далеки друг от друга, а не тогда, когда они находятся рядом друг с другом.
По сравнению с экранировкой электрического заряда, рост интенсивности сильного взаимодействия с расстоянием противоречит интуиции. Как так может получиться, что взаимодействие становится сильнее, когда частицы находятся дальше друг от друга? Большинство взаимодействий ослабевает с расстоянием. На самом деле, чтобы доказать это, нужно проделать вычисления, однако можно привести и примеры такого поведения в окружающем мире.
Допустим, некто посылает в бюрократическое учреждение письмо, важность которого какой-то менеджер среднего звена просто не понимает. В этом случае менеджер может раздуть то, что было обычной памятной запиской, в критически важную директиву. Как только менеджер среднего звена модифицировал письмо, оно стало оказывать намного большее влияние, чем то, которое возникло бы, если бы автор письма передал его непосредственно адресату.
Другим примером, показывающим, что взаимодействия на больших расстояниях могут быть сильнее взаимодействий на малых расстояниях, может служить Троянская война. Согласно Илиаде, Троянская война началась после того, как троянский царевич Парис решил сбежать вместе с Еленой, женой спартанского царя Менелая. Если бы Менелай и Парис сразились друг с другом за право обладать Еленой до того, как Парис и Елена сбежали в Трою, война между греками и троянцами могла бы закончиться до того, как она превратилась в эпос. Но поскольку Менелай и Парис оказались далеко друг от друга, они взаимодействовали со многими людьми и собрали большие силы, участвовавшие в очень кровопролитных греко-троянских битвах.
Как ни удивительно, рост сильных взаимодействий с расстоянием достаточен для объяснения всех характерных свойств сильных взаимодействий. Это объясняет, почему сильное взаимодействие столь сильно, чтобы удерживать кварки связанными внутри протонов и нейтронов, и кварки, захваченные струями: сильное взаимодействие растет на больших расстояниях до момента, когда испытывающая его частица не может быть удалена слишком далеко от других сильновзаимодействующих частиц. Фундаментальные сильновзаимодействующие частицы, например кварки, никогда не обнаруживаются в изоляции.
Достаточно удаленные друг от друга кварк и антикварк запасли бы колоссальное количество энергии, настолько большое, что было бы энергетически выгоднее создать дополнительные физические кварки и антикварки между исходными, чем сохранить их изолированными. Если бы вы попробовали раздвинуть кварк и антикварк еще дальше друг от друга, из вакуума стали бы рождаться новые кварки и антикварки. Это напоминает автомобильное движение в городе Бостоне. Вам никогда не удастся двигаться так, чтобы промежуток между вашей машиной и машиной спереди превышал длину машины, так как этот промежуток тут же занимает какая-то машина из соседней полосы. Так и новые кварки и антикварки будут болтаться вблизи исходных, так что ни один отдельный кварк или антикварк не станет более изолированным, чем в начале, — рядом всегда найдутся другие кварки и антикварки.
Так как сильное взаимодействие на больших расстояниях столь велико, что оно не позволяет сильновзаимодействующим частицам изолироваться друг от друга, частицы, несущие сильный заряд, всегда оказываются окруженными другими заряженными частицами, образуя нейтральные по отношению к сильному взаимодействию комбинации. Поэтому мы никогда не наблюдаем изолированные кварки. Наблюдаются только сильно связанные адроны и струи.
Великое объединение
В предыдущем разделе мы рассказали о зависимости сильных, слабых и электромагнитных взаимодействий от расстояния. В 1974 году Джорджи и Глэшоу высказали смелое предположение, что все эти три взаимодействия изменяются с расстоянием и энергией так, что при высокой энергии они объединяются в единое взаимодействие. Авторы назвали свою теорию ТВО (аббревиатура теории Великого объединения). Поскольку симметрия сильного взаимодействия меняет местами три цвета кварков (как обсуждалось в гл. 7), а симметрия слабого взаимодействия меняет местами разные пары частиц, симметрия ТВО действует и меняет местами все типы частиц Стандартной модели — кварки и лептоны.
Согласно теории Великого объединения Джорджи и Глэшоу, на ранней стадии эволюции Вселенной, когда температура и энергия были экстремально большими (температура превышала сто триллионов триллионов (1026) градусов, а энергия была больше тысячи триллионов (1015) ГэВ), интенсивность каждого из трех взаимодействий была одинаковой, и все три негравитационные силы сливались в единую «Силу».
В процессе эволюции Вселенной температура падала, и единое взаимодействие расщепилось на три отдельных взаимодействия, каждое со своей зависимостью от энергии, следуя которой они эволюционировали в известные нам сейчас три негравитационных взаимодействия. Хотя изначально взаимодействия были единой силой, из-за разного влияния на каждое из них виртуальных частиц они завершили эволюцию с очень разными интенсивностями при низких энергиях.
Три взаимодействия похожи на тройню, родившуюся из одного оплодотворенного яйца, но выросшую и превратившуюся в трех довольно разных личностей. Один член тройни мог бы быть панком-рокером с выкрашенными волосами, закрученными в виде острых пичков, другой — морским пехотинцем, подстриженным под бобрик, а третий — художником с длинным конским хвостом. Тем не менее все имеют одинаковую ДНК, и в младенчестве их было трудно отличить друг от друга.
В ранней Вселенной три взаимодействия также были неразличимыми. Но они расщепились за счет механизма спонтанного нарушения симметрии. Точно так же, как механизм Хиггса расщепил электрослабую симметрию, оставив ненарушенным только электромагнитное взаимодействие, этот же механизм разрушил симметрию ТВО, оставив три отдельных взаимодействия, которые мы сейчас наблюдаем.
Единая интенсивность взаимодействия при большой энергии есть необходимое условие ТВО. Это означает, что три графика, представляющие интенсивность взаимодействия как функцию энергии, должны обязательно пересечься при одной и той же энергии. Но мы уже знаем, как зависят от энергии интенсивности трех негравитационных сил. Поскольку квантовая механика утверждает, что большое расстояние эквивалентно малой энергии, а малое расстояние — большой[120], результаты предыдущего раздела можно с равным успехом интерпретировать в терминах энергии. При низких энергиях электромагнитные и слабые взаимодействия менее сильны, чем сильное взаимодействие, но с ростом энергий они усиливаются, в то время как сильное взаимодействие ослабевает.
Иными словами, интенсивности всех трех негравитационных взаимодействий становятся все более сравнимыми при больших энергиях. Постепенно они должны сходиться к единой интенсивности. Это означало бы, что три линии, представляющие интенсивность взаимодействий как функцию энергии, пересекаются при высоких энергиях.
Две линии, пересекающиеся в одной точке, — не слишком удивительный результат, такое должно произойти, когда линии сближаются друг с другом. Но три линии, встречающиеся в одной точке, — это либо поразительное совпадение, либо свидетельство чего-то более значимого. Если взаимодействия действительно сливаются, их единая интенсивность может быть указанием на то, что при больших энергиях существует лишь один тип сил, и в этом случае мы будем иметь единую теорию.
Хотя до сего дня объединение взаимодействий остается гипотезой, если оно окажется верным, то станет решающим скачком к более простому описанию природы. Так как принципы объединения столь захватывающи, физики изучают интенсивность трех взаимодействий при больших энергиях, чтобы убедиться, сходятся они или нет. Если вернуться в 1974 год, никто тогда не измерял интенсивности трех негравитационных взаимодействий с очень большой точностью. Говард Джорджи, Стивен Вайнберг и Хелен Куинн (она была в те годы постдоком без оклада в Гарварде, а сейчас работает в Станфордском центре линейного ускорителя и является президентом Американского физического общества) использовали доступные в те годы неточные измерения и провели вычисления методом ренормализационной группы, чтобы экстраполировать интенсивность взаимодействий к большим энергиям. Они обнаружили, что три линии, представляющие интенсивности негравитационных взаимодействий, похоже, действительно сходятся в одну точку.
Знаменитая статья Джорджи — Глэшоу 1974 года о теории Великого объединения начинается словами: «Мы представляем ряд гипотез и догадок, неизбежно приводящих к выводу… что все взаимодействия элементарных частиц (сильное, слабое и электромагнитное) являются проявлениями одного и того же фундаментального взаимодействия, содержащего единственную константу связи. Наша гипотеза может оказаться неверной, а догадки неубедительными, но однозначность и простота нашей схемы — достаточные причины, чтобы рассматривать ее серьезно». Возможно, это были не самые скромные слова. Однако Джорджи и Глэшоу на самом деле и не думали, что однозначность и простота — достаточные основания для того, чтобы считать, что их теория правильно описывает природу. Они хотели также получить экспериментальное подтверждение.
Хотя требовалось колоссальное усилие воображения, чтобы экстраполировать Стандартную модель на энергию, в десять триллионов раз большую, чем используемая, ученые осознали, что их экстраполяция имеет^проверяемое следствие. В своей статье Джорджи и Глэшоу объяснили, что их ТВО «предсказывает, что протон распадается», и экспериментаторы должны попробовать проверить это предсказание.
Единая теория Джорджи и Глэшоу предсказывает, что протоны не живут вечно. После очень долгого промежутка времени они должны распадаться. В рамках Стандартной модели такое не может случиться никогда. Обычно кварки и лептоны различаются по взаимодействиям, которые они испытывают. Но в теории Великого объединения все взаимодействия по сути одинаковы. Таким образом, так же как u-кварк может превратиться в d-кварк за счет слабого взаимодействия, кварк должен быть способен превратиться в лептон за счет единого взаимодействия. Это означает, что если идея ТВО верна, общее число кварков во Вселенной не должно оставаться неизменным, а кварк может превращаться в лептон, порождая распад протона — частицы, составленной из трех кварков.
Так как протон может распадаться в рамках ТВО, связывающей кварки и лептоны, вся знакомая нам материя является в конце концов нестабильной. Однако вероятность распада протона очень мала — его время жизни намного превышает возраст Вселенной. Это означает, что даже такое яркое событие, как распад протона, имеет мало шансов быть зарегистрированным, так как оно происходит слишком редко.
Чтобы получить свидетельства распада протона, физики должны соорудить очень большие установки и провести на них долго длящиеся эксперименты, в которых изучается огромное число протонов. В этом случае, даже если каждый отдельный протон распадается неохотно, большое число протонов резко увеличит шансы, что эксперимент сможет зарегистрировать распад одного из них. Даже если вероятность выиграть в лотерею очень мала, она станет намного большей, если вы купите миллионы билетов.
Физики действительно построили такие большие многопротонные экспериментальные установки, в том числе установку Ирвин/Мичиган/Брукхейвен (ИМБ), расположенную в шахте Хоумстейк в Южной Дакоте, и установку Камиоканде — цистерну с водой и детекторы, спрятанные под землей на километровой глубине в Камиока, Япония. Хотя распад протона — исключительно редкий процесс, эти эксперименты уже должны были подтвердить его существование, если ТВО Джорджи — Глэшоу верна. К сожалению, несмотря на честолюбивые замыслы, никто пока что не сумел обнаружить такой распад.
Это не означает, что объединение взаимодействий исключается. На самом деле, благодаря более точным измерениям взаимодействий, мы знаем теперь, что исходная модель, предложенная Джорджи и Глэшоу, почти наверняка неверна, и объединить взаимодействия может только расширенная версия Стандартной модели. Оказывается, что в таких моделях предсказывается более долгое время жизни протона, так что до сих пор распад протона и не должен был быть обнаружен.
Сегодня мы на самом деле не знаем, является ли объединение взаимодействий истинным свойством природы, или, если это так, то что оно означает. Вычисления показывают, что объединение может происходить в нескольких моделях, о которых я поговорю ниже, включая суперсимметричные модели, модели с дополнительными измерениями Хоржавы — Виттена, и модели с закрученными дополнительными измерениями, которые развивали Раман Сундрум и я. Модели с дополнительными измерениями особенно занимательны, так как они могут привести в общее стадо гравитацию и действительно объединить все известные взаимодействия. Эти модели также важны потому, что в исходных моделях объединения предполагалось, что в области выше масштаба слабых взаимодействий могут быть найдены только новые частицы с массами, имеющими массы порядка масштаба ТВО[121]. Новые модели показывают, что объединение может произойти даже в том случае, если существует много новых частиц, которые могут рождаться при энергиях выше масштаба слабых взаимодействий.
Однако, как ни восхитительна идея объединения взаимодействий, физики в наше время разделились во мнениях о ее теоретических достоинствах согласно тому, предпочитают ли они в физике подход «сверху вниз» или «снизу вверх». Идея ТВО воплощает подход «сверху вниз». Джорджи и Глэшоу сделали смелое предположение об отсутствии частиц с массой между тысячью ГэВ и тысячью триллионов ГэВ и построили гипотетическую теорию, основанную на этом предположении. Великое объединение было первым шагом к началу споров среди физиков-частичников, которые продолжаются сейчас в отношении теории струн. Обе теории экстраполируют физические законы от измеряемых энергий до энергий, по меньшей мере в десять триллионов раз больших. Позднее Джорджи и Глэшоу усомнились в отношении подхода «сверху вниз», который представляют теория струн и поиск Великого объединения. С тех пор они развернули свой курс и сейчас сосредоточились на низкоэнергетической физике.
Хотя единые теории имеют ряд привлекательных черт, я не уверена, приведет ли их изучение к правильным взглядам на природу. Энергетическая щель между тем, что мы знаем, и тем, куда мы экстраполируем, чудовищно велика, и можно вообразить кучу возможностей того, что может случиться между этими значениями. В любом случае, пока распад протона не будет обнаружен (если это вообще когда-нибудь произойдет), будет невозможно с уверенностью установить, действительно ли взаимодействия объединяются при высокой энергии. До тех пор теория остается в области великой, но теоретической, догадки.
Что стоит запомнить
• Виртуальные частицы — это частицы, имеющие те же заряды, что и реальные физические частицы, но с энергиями которых не все в порядке.
• Виртуальные частицы существуют лишь очень короткое время; они постоянно одалживают энергию у вакуума — состояния Вселенной без частиц.
• Квантовые вклады в физические процессы возникают от виртуальных частиц, взаимодействующих с реальными частицами. Эти вклады от виртуальных частиц влияют на взаимодействия реальных частиц за счет рождения и уничтожения, и действуют как посредники между реальными частицами.
• Анархический принцип утверждает, что при рассмотрении свойств частиц всегда должны учитываться квантовые вклады.
• В единой теории единственное взаимодействие при больших энергиях превращается в три известных негравитационных взаимодействия при низких энергиях. Чтобы три взаимодействия объединились, они должны иметь при высоких энергиях одну общую интенсивность.
Глава 12
Проблема иерархии: единственная эффективная «теория просачивания»
The highway is for gamblers, better use your sense.
Take what you have gathered from coincidence.
Bob Dylan[122]
Бесславный конец настиг Икара Рашмора III, врезавшегося на своем великолепном новом порше в фонарный столб. Тем не менее он был счастлив на небесах, так как мог все время играть в разные игры. В глубине души он был игроком.
Однажды сам Господь пригласил Икара поучаствовать в довольно странной игре. Бог предложил ему написать шестнадцатизначное число. Бог будет метать божественную икосаэдрическую игральную кость. В противоположность обычной кубической игральной кости с шестью гранями, у этой число граней было равно двадцати, и на гранях были нанесены по два раза цифры от 0 до 9. Бог пояснил, что Он будет шестнадцать раз метать кость, и строить шестнадцатизначное число, записывая один за другим результаты бросания. Если Бог и Икар придут к одному и тому же огромному числу, т. е. если все его цифры выпадут в правильном порядке, Бог выиграл. Если цифры не будут точно такими же, т. е. если хотя бы одна цифра не совпадет, то выиграл Икар.
Бог начал метать, первой выпала грань с цифрой 4. Это совпадало с первой цифрой числа, загаданного Икаром: 4715 031495526312. Икар удивился тому, что Бог метнул правильно, так как шансы были один к десяти. Тем не менее он был совершенно уверен, что вторая или третья цифры будут неправильными; шансы на то, что Бог выбросит последовательно обе правильные цифры, были лишь один к ста.
Бог метнул кость второй и третий раз. Он выбросил цифры 7 и 1, которые также были правильными. Бог продолжал метать кость до тех пор, пока не выбросил в правильном порядке все шестнадцать цифр. Икар был потрясен. Шансы этого события составляли всего 1 к 10 000 000 000 000 000. Как Богу удалось выиграть?
Икар немного рассердился (никто не может сильно сердиться на Небесах) и спросил, как могло произойти столь смехотворно невероятное событие. Бог глубокомысленно ответил: «Я — единственный, кто мог надеяться на выигрыш, так как Я всеведущ и всесилен. Однако ты должен был слышать, что я не люблю играть в кости».
И вместе с этими словами на облаке возникла надпись «ИГРЫ ЗАПРЕЩЕНЫ». Икар пришел в ярость (конечно, немножко). Он не просто проиграл, он проиграл само право играть.
Надеюсь, что к этому моменту вы уже довольно много узнали о физике частиц и ряде красивых теоретических идей, с помощью которых физики построили Стандартную модель. Эта модель превосходно объясняет множество разных экспериментальных результатов. Однако она покоится на неустойчивом основании, содержащем глубокую и важную загадку, одну из тех, решение которых приводит к новому проникновению в фундаментальную структуру материи. В этой главе мы исследуем эту загадку, известную среди физиков-частичников как проблема иерархии.
Проблема не в том, что предсказания Стандартной модели не согласуются с экспериментальными результатами. Массы и заряды, связанные с электромагнитными, слабыми и сильными взаимодействиями, были проверены с невероятной точностью. Эксперименты на коллайдерах в ЦЕРНе, SLAC и Фермилабе с исключительной точностью подтвердили предсказания Стандартной модели для взаимодействий и вероятностей распада известных частиц. И интенсивности взаимодействий в Стандартной модели тоже уже не являются загадкой. В действительности, их взаимосвязь друг с другом дает подсказки и лежит в основе идеи о теории Великого объединения. Наконец, механизм Хиггса превосходно объясняет, каким образом вакуум нарушает электрослабую симметрию и придает массы калибровочным бозонам W и Z, а также кваркам и лептонам.
Однако, если приглядеться более внимательно, то даже в самых идеальных семьях могут обнаружиться подводные течения и скрытые трения. Несмотря на безупречные манеры и счастливый вид, ее подспудно может разъедать разрушительный секрет. У Стандартной модели как раз есть такой скелет в шкафу. Если вы некритично предположите, что интенсивности электромагнитного и слабого взаимодействий, а также массы калибровочных бозонов принимают те значения, которые измерены на опыте, то все результаты будут согласовываться с предсказаниями. Но, как мы скоро увидим, несмотря на то что массовый параметр (масштаб массы слабых взаимодействий, определяющий массы элементарных частиц) очень хорошо измерен, его значение в десять миллионов миллиардов раз (на шестнадцать порядков величины) меньше, чем та масса, которую физики ожидали бы получить из общих теоретических соображений. Любой физик, который попытался бы предугадать значение масштаба массы слабых взаимодействий, основываясь на теории высоких энергий, получил бы совершенно неверное значение этого параметра (и, следовательно, всех масс частиц). Кажется, что масса возникает из тумана. Эта загадка — проблема иерархии — представляет зияющий провал в нашем понимании физики частиц.
Во Введении я ставила проблему иерархии как вопрос о том, почему так слабо тяготение, но сейчас мы увидим, что эту проблему можно переформулировать как вопрос о том, почему так мала масса хиггсовской частицы и, следовательно, массы слабых калибровочных бозонов. Для того чтобы эти массы приняли свои измеряемые на опыте значения, Стандартная модель должна на полном серьезе включать такую чепуху, как игру в кости на правильное угадывание шестнадцатизначного числа. Несмотря на многочисленные достижения, для объяснения масс известных элементарных частиц Стандартной модели приходится прибегать к такой отъявленной подтасовке.
В этой главе мы объясняем саму проблему и то, почему я и большинство других теоретиков-частичников считаем ее столь важной. Как следует из проблемы иерархии, что бы ни было ответственно за нарушение электрослабой симметрии, это значительно интереснее, чем представленный в гл. 10 пример с двумя хиггсовскими полями. Все возможные решения проблемы включают новые физические принципы, и очень похоже, что решение приведет физиков к открытию новых фундаментальных частиц и законов. Установление того, что играет роль хиггсовского поля и нарушает электрослабую симметрию, откроет один из самых богатых разделов новой физики из всех, которые нам удавалось поймать. Почти наверняка новые физические явления проявятся при энергии порядка 1 ТэВ. Экспериментальные проверки конкурирующих гипотез не за горами, так что лет через десять произойдет драматический пересмотр нашего понимания фундаментальных физических законов, включая те, которые будут к тому времени открыты.
Проблема иерархии говорит нам, что перед экстраполяцией физики в область сверхвысоких энергий мы должны внимательно рассмотреть по крайней мере одну неотложную проблему при низкой энергии. В течение последних тридцати лет или около того теоретики-частичники занимались поисками структуры, предсказывающей и защищающей масштаб энергии слабых взаимодействий — сравнительно низкую энергию, при которой происходит нарушение электрослабой симметрии. И я, и другие ученые полагают, что должно существовать решение проблемы иерархии, которое обеспечит одну из лучших путеводных нитей к тому, что лежит за пределами Стандартной модели. Чтобы понять мотивацию тех теорий, которые я сейчас представлю, полезно кое-что знать об этой несколько технической, но очень важной проблеме. Поиск ее решения уже привел нас к исследованию новых физических понятий, которые используются в следующих главах, и решение почти наверняка приведет к пересмотру наших теперешних взглядов.
Прежде чем рассмотреть самую общую версию проблемы иерархии, рассмотрим сначала эту проблему в контексте теории Великого объединения, в рамках которой проблема была впервые сформулирована и где ее несколько проще понять. Затем мы посмотрим на проблему в максимально широком (и всеохватывающем) контексте и увидим, почему она в конце концов сводится к слабости гравитации по сравнению со всеми другими известными взаимодействиями.
Проблема иерархии в ТВО
Представьте себе, что вы зашли в гости к одному своему очень высокому приятелю ростом под 2 метра и обнаружили, что у него есть брат-близнец ростом всего полтора метра. Это может показаться удивительным. Естественно предполагать, что и ваш приятель, и его брат, имеющие одинаковый набор генов, будут одного роста. А теперь представьте еще более поразительную картину: вы входите в дом вашего приятеля и обнаруживаете, что рост его брата в десять раз меньше или в десять раз больше. Это будет действительно очень странно.
Мы не думаем, что все частицы должны иметь одинаковые свойства. Но тем не менее разумно считать, что частицы, испытывающие одинаковые взаимодействия, чем-то похожи. Например, мы ожидаем, что их массы сравнимы. Так же как есть веские основания ожидать, что члены одной семьи имеют примерно одинаковый рост, физики-частичники имеют веские основания ожидать, что массы частиц в единой теории, например в ТВО, также сравнимы. Но массы частиц в ТВО совсем разные: даже те частицы, которые испытывают похожие взаимодействия, должны обладать чудовищно разными массами. Эта разница отнюдь не сводится к множителю десять, расхождение между массами соответствует множителю десять триллионов.
Проблема ТВО состоит в том, что хотя нарушающая электрослабую симметрию хиггсовская частица должна быть «легкой», с массой, приблизительно равной масштабу массы слабых взаимодействий, ТВО связывает хиггсовскую частицу с другой частицей, взаимодействующей за счет сильного взаимодействия. Но эта новая частица в ТВО должна быть невероятно тяжелой, с массой, примерно равной масштабу масс ТВО. Иными словами, две частицы, которые по предположению связаны симметрией (симметрией взаимодействия ТВО), должны иметь чудовищно различающиеся массы.
Две разные, но связанные частицы должны в рамках ТВО возникать совместно, так как слабое и сильное взаимодействия при высоких энергиях должны быть взаимозаменяемы. В этом заключается главная идея единой теории — все взаимодействия должны в конце концов стать одинаковыми. Таким образом, когда сильные и слабые взаимодействия объединяются, каждая частица, испытывающая слабое взаимодействие, в том числе хиггсовская частица, должна образовать пару с другой частицей, испытывающей сильное взаимодействие и обладающей взаимодействиями, аналогичными тем, которые есть у исходной хиггсовской частицы. Однако с новой частицей, участвующей в сильных взаимодействиях и связанной с хиггсовской частицей, возникает серьезная проблема.
Обладающая сильным зарядом частица-партнер хиггсовской частицы может одновременно взаимодействовать с кварком и лептоном, что может привести к распаду протона, даже более быстрому, чем предсказывает ТВО. Чтобы избежать слишком быстрого распада, сильно взаимодействующая частица, обмен которой между двумя кварками и двумя лептонами должен происходить для того, чтобы имел место распад протона, должна быть невероятно тяжелой. Из полученного в настоящее время предела на время жизни протона следует, что сильновзаимодействующий партнер хиггсовской частицы (если он существует в природе) должен иметь массу, сравнимую с масштабом масс ТВО, т. е. около одного миллиона миллиардов ГэВ. Если эта частица существует, то не будь она столь тяжелой, вы и эта книга распались бы прежде, чем вы дочитаете эту фразу.
Однако мы уже знаем, что для того чтобы придать слабым калибровочным бозонам измеряемые на опыте массы, обладающая слабым зарядом хиггсовская частица должна быть легкой (около 250 ГэВ). Таким образом, из экспериментальных ограничений следует, что масса хиггсовской частицы должна чудовищно отличаться от массы хиггсовского партнера, взаимодействующего сильным образом. Сильно заряженная хиггсовская частица, которая в рамках единой теории обладает очень похожими взаимодействиями, что и слабо заряженная хиггсовская частица, должна иметь совершенно другую массу, в противном случае мир не имел бы ничего общего с тем, который мы видим. Это колоссальное расхождение между двумя массами (одна в десять триллионов раз больше другой) очень трудно объяснить, особенно в рамках единой теории, в которой как слабо заряженная, так и сильно заряженная хиггсовские частицы имеют, по предположению, похожие взаимодействия.
В большинстве единых теорий единственный способ сделать одну частицу тяжелой, а другую — легкой, состоит во введении огромного подгоночного множителя. Нет никакого физического принципа, который предсказывал бы, что массы должны быть столь различны. Единственный способ заставить схему работать — это ввести очень аккуратно выбранное число. Это число должно иметь тринадцать точных значащих цифр, в противном случае либо протон будет распадаться, либо массы слабых калибровочных бозонов будут слишком велики.
Физики-частичники называют необходимую подгонку тонкой настройкой. Эта настройка возникает в том случае, когда вы подгоняете параметр, чтобы получить точно то значение, которое хотите. Слово «настройка» используется потому, что процесс напоминает настройку фортепианной струны, чтобы получить точно нужный звук. Но если вы хотите получить правильную частоту в несколько сотен герц с точностью в тринадцать значащих цифр, вы должны слушать звук в течение десяти миллиардов секунд, т. е. тысячу лет, чтобы убедиться, что все правильно. Точность в тринадцать значащих цифр достичь трудно.
Я могла бы привести и другие аналогии точной настройки, но поверьте, они покажутся вам надуманными. Например, рассмотрим очень большую фирму, в которой один сотрудник отвечает за расходы, а другой — за доходы. Допустим, что эти люди никогда друг с другом не общаются, но требуется, чтобы в конце года расходы почти в точности равнялись доходам, так чтобы на счету остались какие-то копейки, в противном случае фирму закроют. Да, это действительно надуманный пример. Нетрудно понять, почему. Никакие осмысленные ситуации не зависят от тонкой настройки, никто не хочет, чтобы его судьба (или судьба его бизнеса) зависела от столь маловероятных совпадений. Точно так же любая теория Великого объединения с легкой хиггсовской частицей сталкивается с такой проблемой зависимости. Очень маловероятно, что теория, в которой физические предсказания столь чувствительно зависят от параметра, является полной правдой.
Но единственный способ получить достаточно малую массу хиггсовской частицы в простейшей ТВО — это подогнать теорию. Модель ТВО не предлагает никакой хорошей альтернативы. Это серьезная проблема для большинства моделей, совершающих объединение в четырех измерениях, и многие физики, включая меня, из-за этого не уверены в унификации взаимодействий.
Но проблема иерархий еще хуже. Даже если вы хотите просто предположить, без какого-либо обоснования, что одна частица легкая, а другая необычайно тяжелая, вы все равно столкнетесь с проблемами, вызываемыми квантово-механическими поправками, или просто квантовым вкладом. Эти квантовые вклады должны добавляться к классической массе, чтобы определить истинную, физическую массу, которую должна иметь хиггсовская частица в реальном мире. И эти вклады в общем случае намного больше, чем та масса в несколько сотен ГэВ, которую требует хиггсовская частица.
Прежде чем перейти к следующему разделу, где обсуждаются квантовые вклады, основанные на понятии виртуальных частиц и квантовой механике, хочу предупредить вас, что интуитивно это будет сложно понять. Не пытайтесь искать классическую аналогию, так как то, чем мы собираемся заняться, представляет собой чисто квантово-механический эффект.
Квантовые вклады в массу хиггсовской частицы
В предыдущей главе было объяснено, почему в общем случае частица не может без изменений пролететь сквозь пространство. По дороге могут возникать и исчезать виртуальные частицы, оказывая влияние на путь исходной частицы. Квантовая механика утверждает, что мы всегда должны суммировать вклады от всех возможных путей в значение любой физической величины.
Как мы видели, такие виртуальные частицы приводят к тому, что интенсивность взаимодействий становится зависящей от расстояния, что было измерено и хорошо согласуется с предсказаниями. Те же типы квантовых вкладов, которые приводят к зависимости взаимодействий от энергии, влияют и на величину масс частиц. Но в отличие от интенсивностей взаимодействий, влияние виртуальных частиц на массу хиггсовской частицы противоречит тому, что эксперимент требует от теории. Квантовые вклады оказываются слишком большими.
Так как хиггсовская частица взаимодействует с тяжелыми частицами, масса которых достигает масштаба масс ТВО, ряд путей, по которым она перемещается, включает вакуум, выплевывающий виртуальную тяжелую частицу и ее античастицу, так что хиггсовская частица в процессе движения на время превращается в эти частицы (рис. 61). Тяжелые частицы без предупреждения возникают и исчезают в вакууме и влияют на движение хиггсовской частицы. Они — преступники, ответственные за большие квантовые поправки.
Квантовая механика утверждает, что если мы хотим определить массу, которой реально обладает хиггсовская частица, нам нужно добавить такие пути с виртуальными частицами к единственному пути без этих частиц. Проблема состоит в том, что пути, содержащие виртуальные тяжелые частицы, порождают вклады в массу хиггсовской частицы того же порядка, что и массы тяжелых частиц в ТВО, т. е. на тринадцать порядков величины больше желаемой массы. Все эти колоссальные квантово-механические вклады виртуальных тяжелых частиц нужно добавить к классическому значению массы хиггсовской частицы, чтобы получить физическое значение, получаемое при измерении и равняющееся приблизительно 250 ГэВ, что приведет к правильным значениям масс слабых калибровочных бозонов. Это означает, что хотя каждый отдельный вклад ТВО в массу на тринадцать порядков больше, чем нужно, когда мы сложим все эти огромные вклады, часть из которых положительна, а другая часть отрицательна, мы получим примерно 250 ГэВ. Если с хиггсовской частицей взаимодействует хотя бы одна виртуальная тяжелая частица, неизбежно возникает проблема.
Если, как в предыдущей главе, мы проведем аналогию между виртуальными частицами и сотрудниками некоего учреждения, например, Службой иммиграции и натурализации США, работа которых состоит в том, чтобы выявлять и откладывать документы от подозрительных лиц, то окажется, что вместо этого они занимаются тщательным изучением всех документов от всех лиц. Вместо двухуровневой системы, в которой часть документов быстро рассматривается, а другая часть задерживается, все документы рассматриваются одинаково. Аналогично, механизм Хиггса требует, чтобы «учреждение» виртуальных частиц оставляло часть частиц тяжелыми, но позволяло другим, в том числе хиггсовской частице, быть легкими. Вместо этого квантовые пути, включающие виртуальные частицы, как сверхусердные работники, дают сравнимые вклады в массы всех частиц. Итак, мы ожидаем, что все частицы, в том числе хиггсовская частица, должны быть такими же тяжелыми, как масштаб масс ТВО.
Если не привлекать новую физику, единственный (и очень неудовлетворительный) путь решения проблемы чрезмерно большой массы хиггсовской частицы заключается в предположении, что ее классическая масса принимает точно такое значение (оно может быть и отрицательным), которое сократит большую квантовую поправку к массе хиггсовской частицы. Параметры теории, определяющей массы частиц, должны быть таковы, что все вклады суммируются, приводя к очень малому числу, даже несмотря на то, что каждый отдельный вклад очень большой. Это и есть процесс тонкой настройки, который упоминался в предыдущем разделе.
Такая схема потенциально возможна, но крайне маловероятно, что она имеет место в действительности. Ведь это не просто вопрос о небольшой подгонке параметра, с тем чтобы получить правильную массу. Требуемая подгонка колоссальна и столь же колоссально точна: любой параметр, имеющий точность меньше тринадцати знаков, приведет к резко неправильным результатам. Уточним, что такая неестественная подгонка не имеет отношения к вопросу о точном измерении какой-то величины, например скорости света. Обычно качественные предсказания не зависят от конкретных значений параметра. Только одно значение будет приводить к точной величине, которую мы измеряем, но мир не сильно изменился бы, если бы этот параметр принял чуть отличающееся значение. Если бы ньютоновская постоянная тяготения (определяющая интенсивность гравитации) имела значение, отличающееся от известного всего на 1 %, не произошло бы никаких резких изменений.
С другой стороны, в ТВО достаточно малого изменения параметра для того, чтобы полностью разрушить как качественные, так и количественные предсказания теории. Физические следствия значения массы хиггсовской частицы, нарушающей электрослабую симметрию, невероятно чувствительны к значению параметра. Практически для всех значений этого параметра не существует иерархии между массой ТВО и масштабом массы слабых взаимодействий, и строение мира и жизнь, покоящиеся на этой иерархии, были бы невозможны. Если бы этот параметр сдвинулся бы всего на 1 %, масса хиггсовской частицы была бы намного больше. Тогда массы слабых калибровочных бозонов, а также массы всех других частиц были бы много больше, так что следствия Стандартной модели не имели бы ничего общего с тем, что мы видим.
Проблема иерархии в физике частиц
В предыдущем разделе было рассказано о великой загадке — проблеме иерархии в ТВО. Но истинная проблема иерархии еще хуже. Хотя ТВО первая привлекла внимание физиков к проблеме иерархии, виртуальные частицы будут генерировать чересчур большие вклады в массу хиггсовской частицы даже в теории без частиц с массой ТВО. Даже Стандартная модель находится под подозрением.
Дело в том, что теория, содержащая Стандартную модель в комбинации с теорией тяготения, содержит два очень различающихся энергетических масштаба. Один — это масштаб энергии слабых взаимодействий, равный 250 ГэВ, т. е. энергия, при которой происходит нарушение электрослабой симметрии. Если энергия частиц меньше этого масштаба, становятся явными явления нарушения электрослабой симметрии, а слабые калибровочные бозоны и элементарные частицы имеют массу.
Другим уровнем энергии является планковский масштаб, который на шестнадцать порядков величины, т. е. в десять миллионов миллиардов (1016) раз, больше, чем масштаб энергии слабых взаимодействий. Планковский масштаб энергий определяет интенсивность гравитационных взаимодействий: закон Ньютона утверждает, что интенсивность обратно пропорциональна квадрату этой энергии. И так как интенсивность тяготения мала, планковский масштаб масс (связанный с планковским масштабом энергии формулой E = mc2) большой. Огромный планковский масштаб масс эквивалентен необычайно слабому тяготению.
До сих пор планковский масштаб масс не возникал в наших обсуждениях физики частиц, так как тяготение настолько мало, что в большинстве относящихся к физике частиц вычислений им можно было спокойно пренебречь. Но именно на этот вопрос хотят получить ответ физики-частичники: почему тяготение столь слабо, что им можно пренебречь в вычислениях по физике частиц? Другой способ сформулировать проблему иерархий состоит в том, чтобы спросить, почему планковский масштаб масс столь огромен, почему он в десять миллионов миллиардов раз больше, чем массы, относящиеся к масштабам физики частиц, которые меньше нескольких сотен ГэВ?
Чтобы дать вам пищу для сравнения, рассмотрим гравитационное притяжение между двумя частицами малой массы, например, между парой электронов. Гравитационное притяжение примерно в сто миллионов триллионов триллионов триллионов раз слабее электрического отталкивания между этими частицами. Два типа сил будут сравнимы, если электроны будут тяжелее в десять миллиардов триллионов раз. Это колоссальное число, оно сравнимо с тем, сколько раз вы сможете приложить остров Манхеттен непрерывной цепочкой на расстоянии, равном размеру видимой Вселенной.
Планковский масштаб масс неизмеримо больше, чем масса электрона и массы всех других известных нам частиц, и это указывает на то, что тяготение намного слабее других известных взаимодействий. Но почему должно быть такое огромное расхождение между интенсивностями большинства взаимодействий, или эквивалентно, почему планковский масштаб масс настолько огромен по сравнению с массами известных частиц?
Для специалистов по физике частиц трудно смириться с огромным отношением планковского масштаба масс к слабому масштабу масс, составляющим величину порядка десяти миллионов миллиардов. Это отношение больше, чем число минут, прошедших с момента Большого взрыва; оно в тысячу раз больше, чем число детских шариков, которые можно выложить от Земли до Солнца. Это число более чем в сто раз больше числа центов в бюджетном дефиците США! Почему же две массы, описывающие одну и ту же физическую систему, должны настолько различаться?
Если вы не специалист по физике частиц, вам может показаться, что все это не слишком существенная проблема, даже если эти числа очень велики. В конце концов, мы не обязаны объяснять все, и две массы могут быть разными без всяких особых причин. Но ситуация на самом деле намного хуже, чем кажется. Речь идет не только о существовании необъясненного огромного отношения масс. В следующем разделе мы увидим, что в рамках квантовой теории поля любая частица, взаимодействующая с хиггсовской частицей, может участвовать в виртуальном процессе, приводящем к росту массы хиггсовской частицы до значения порядка планковского масштаба масс 1019 ГэВ.
На самом деле, если бы вы попросили любого честного физика-частичника, знающего интенсивность гравитации, но ничего не знающего об измеренных массах слабых калибровочных бозонов, оценить массу хиггсовской частицы, используя квантовую теорию поля, он предсказал бы для хиггсовской частицы, и следовательно для слабых калибровочных бозонов, значения масс, в десять миллионов миллиардов раз большие, чем нужно. Иначе говоря, он заключил бы из своих вычислений, что отношение планковского масштаба масс и массы хиггсовской частицы (т. е. масштаба массы слабых взаимодействий, определяемого массой хиггсовской частицы) должно быть намного ближе к единице, чем к десяти миллионам миллиардов! Его оценка слабой шкалы масс была бы настолько близка к планковской шкале масс, что все частицы были бы черными дырами, а физика частиц в том виде, как мы ее знаем, просто не существовала бы. Хотя у него могло не быть априорных ожиданий как для значений масштаба массы слабых взаимодействий, так и планковского масштаба масс по отдельности, он мог бы использовать квантовую теорию поля для оценки отношения масс, и полностью бы ошибся. Ясно, что в этом месте существует огромное противоречие. В следующем разделе мы объясним его причину.
Виртуальные энергичные частицы
Причина, по которой планковский масштаб масс входит в вычисления квантовой теории поля, довольно тонкая. Как мы видели, планковский масштаб масс определяет интенсивность гравитационного взаимодействия. Согласно закону Ньютона, сила гравитации обратно пропорциональна квадрату планковского масштаба масс, и тот факт, что тяготение столь слабо, показывает, что планковский масштаб масс огромен.
В общем случае, делая предсказания в физике частиц, мы можем не учитывать гравитацию, так как ее влиянием на частицу массой порядка 250 ГэВ можно полностью пренебречь. Если действительно требуется принять во внимание гравитационные эффекты, их можно последовательно учесть, но обычно не в этом находится источник беспокойства. В последующих главах будут объяснены новые, совершенно другие сценарии, в которых гравитация сильна в высших измерениях, и ею нельзя пренебречь. Однако в обычной четырехмерной Стандартной модели пренебрежение гравитацией является стандартной и законной процедурой.
Но планковский масштаб масс играет и другую роль — это та максимальная масса, которую может иметь виртуальная частица в достоверных вычислениях в рамках квантовой теории поля. Если масса частиц превышает планковский масштаб, вычисления станут недостоверными, общая теория относительности не будет заслуживать доверия и должна будет быть заменена на более полную теорию, например на теорию струн.
Но если частицы (в том числе виртуальные) имеют массу меньше планковского масштаба, должна быть применима обычная квантовая теория поля, и основанные на ней вычисления должны заслуживать доверия. Это означает, что расчеты, включающие виртуальный топ-кварк (или любую другую виртуальную частицу) с почти такой же большой массой, как планковский масштаб масс, должны быть достоверными.
Проблема иерархии состоит в том, что вклад в массу хиггсовской частицы от виртуальных частиц очень большой массы будет почти таким же большим, как планковский масштаб масс, который в десять миллионов миллиардов раз больше той массы хиггсовской частицы, которую мы хотим, и которая будет давать правильный масштаб массы слабых взаимодействий и правильные массы элементарных частиц.
Если рассмотреть путь типа показанного на рис. 62, в котором хиггсовская частица превращается в пару виртуальных топ-кварка и антитоп-кварка, можно увидеть, что вклад в массу хиггсовской частицы окажется слишком большим. На самом деле любой тип частиц, которые могут взаимодействовать с хиггсовской частицей, может проявиться как виртуальная частица и приобрести массу[123] вплоть до планковского масштаба масс. Результатом учета всех этих возможных путей будут огромные квантовые поправки в массу хиггсовской частицы. Но масса этой частицы должна быть намного меньше.
Физика частиц в ее теперешнем состоянии похожа на слишком эффективную теорию «просачивающегося богатства»[124]. Нетрудно добиться иерархии богатства в экономике. Претворение в жизнь «просачивающейся экономики» никогда не приводило к значительному повышению финансового благосостояния бедных и касалось только уровня доходов верхних классов. Однако в физике просачивание богатства намного более эффективно. Если одна масса велика, то, как показывают квантовые вклады, массы всех элементарных частиц должны быть настолько же велики. Все частицы одинаково обогащаются массой. Но из эксперимента мы знаем, что в нашем мире сосуществуют как большие массы (планковский масштаб масс), так и малые массы (массы частиц).

Без модификации или расширения Стандартной модели теория элементарных частиц может достичь малой массы хиггсовской частицы только за счет сверхъестественного значения ее классической массы. Это значение должно быть невероятно велико и, возможно, отрицательно, так чтобы оно могло в точности сократить большие квантовые вклады. Все массовые вклады в сумме должны приводить к значению 250 ГэВ.
Для того чтобы это произошло, как в рассмотренной выше ТВО, масса должна быть тонко настраиваемым параметром. И этот тонко настраиваемый параметр должен быть поразительно точной подгонкой, специально придуманной так, чтобы дать малую полную массу хиггсовской частицы. Либо квантовые вклады от виртуальных частиц, либо классический вклад должны быть отрицательными и практически равными друг другу по величине. Положительные и отрицательные слагаемые, каждое из которых имеет шестнадцать порядков величины, должны в сумме дать много меньшую величину. Требуемая тонкая настройка, которая должна иметь точность в шестнадцать знаков, намного сильнее, чем тонкая настройка, требуемая для того, чтобы ваш карандаш держался на острие. Вероятность такая же, как случайный выигрыш в игре на угадывание цифр с Икаром.
Специалисты по физике частиц предпочли бы модель, не содержащую тонкой настройки, которая требуется в Стандартной модели для обеспечения малой массы хиггсовской частицы. Хотя мы могли бы примириться с тонкой настройкой от безысходности, но мы бы презирали себя. Тонкая настройка почти наверняка есть акт отчаяния, отражающий наше невежество. Да, иногда неправдоподобные вещи случаются, но они редко случаются тогда, когда мы этого хотим.
Проблема иерархии — самая неотложная из тех, с которыми сталкивается Стандартная модель. Чтобы добавить оптимизма, можно сказать, что проблема иерархии дает ключ к разгадке того, что играет роль хиггсовской частицы и нарушает электрослабую симметрию.
Любая теория, заменяющая теорию двух хиггсовских полей, должна естественно обеспечить или предсказать низкий электрослабый масштаб, в противном случае о ней незачем и размышлять. Многие фундаментальные теории совместимы с наблюдаемыми физическими явлениями, но лишь малая их часть обращается к проблеме иерархий и включает легкую хиггсовскую частицу убедительным образом, не прибегая к тонкой настройке. В то время как задача объединения взаимодействий является соблазнительной теоретической идеей, задача решения проблемы иерархий — это конкретная необходимость, подгоняющая прогресс в изучении сравнительно низких энергий. Этот вызов становится еще более интригующим, если учесть, что все, касающееся проблемы иерархий, должно иметь экспериментальные следствия, которые будут измеримы на БАК, на котором экспериментаторы рассчитывают найти частицы массами от 250 до 1000 ГэВ. Без таких дополнительных частиц нам с этой задачей не справиться. Мы вскоре увидим, что экспериментальными следствиями решения проблемы иерархий может быть наличие суперсимметричных партнеров, или частиц, путешествующих в дополнительных измерениях, которые мы обсудим позднее.
Что стоит запомнить
• Хотя мы знаем, что механизм Хиггса отвечает за массы частиц, простейший известный пример, в котором применяется хиггсовский механизм, содержит обманчивый трюк. В простейшей теории ожидается, что массы слабых калибровочных бозонов и кварков примерно в десять миллионов миллиардов раз больше того значения, которое мы знаем. Проблема иерархии — вопрос о том, почему это не так.
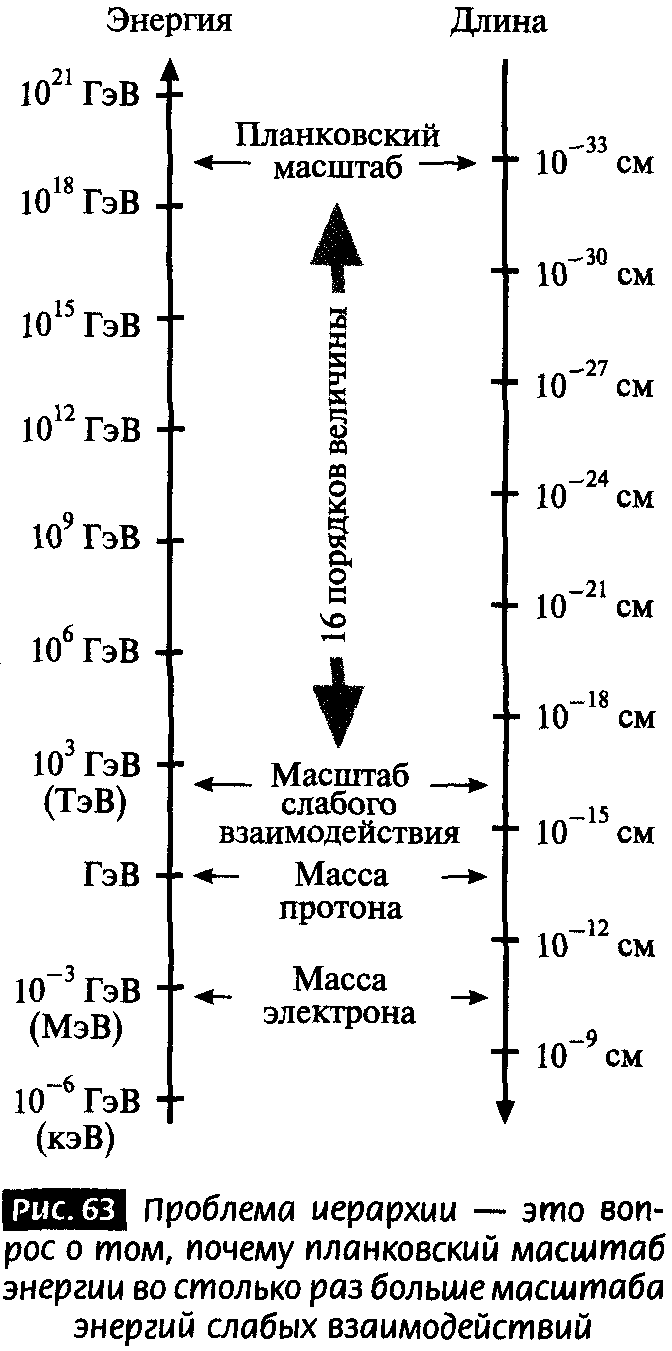
• Проблема иерархии возникает из расхождения между масштабом массы слабых взаимодействий и чудовищным планковский масштабом масс (рис. 63). Последняя масса важна для гравитации — большое значение планковского масштаба масс показывает нам, почему тяготение очень слабо. Таким образом, другой способ сформулировать проблему иерархии — это спросить, почему гравитация столь слаба, намного слабее других негравитационных взаимодействий.
• Любая теория, решающая проблему иерархии, будет экспериментально проверяема, так как она обязательно будет иметь экспериментальные следствия, проверяемые на коллайдерах, работающих при энергиях выше масштаба энергий слабых взаимодействий. Очень скоро такие энергии будут исследоваться на Большом адронном коллайдере.
Глава 13
Суперсимметрия: скачок за пределы Стандартной модели
You were meant for me.
And I was meant for you.
Gene Kelly, («Singing in the Rain»)[125]
Как только Икар попал на небеса, его отправили на семинар, чтобы ознакомить с местными порядками. К своему удивлению, он увидел, что правые религиозные партии действительно следовали своим лозунгам и семейные ценности были той основой, на которой покоился его новый мир. Здесь давным-давно была установлена традиционная структура семьи, основанная на разделении поколений и стабильности браков: аристократы из верхов сочетались браком с дамочками из низов, очаровашек всегда сватали за странных типов, а правдолюбцев женили на красавицах. Всех, также как и самого Икара, вполне устраивал такой порядок.
Но позднее Икар узнал, что социальная структура Небес не всегда была такой устойчивой. первоначально иерархические основы общества нарушали опасные энергетические агенты. Однако на Небесах почти все проблемы решаемы. Бог приставил к каждому персонального ангела-хранителя и ангелы, вместе со своими подопечными, героически работали, отводя угрозу от иерархии и сохраняя общественный порядок.
Однако даже и при таком порядке Небеса не были в полной безопасности. Ангелы превращались в свободных агентов, не имеющих контрактов, которые связывали бы их с одним поколением. Переменчивые ангелы, столь храбро защищавшие иерархию, угрожали сейчас разрушить небесные семейные ценности. Это потрясло Икара, он обнаружил, что вопреки обыденным представлениям, Небеса оказались на удивление неспокойным местом.
В физической терминологии изобилуют слова с приставкой супер[126]. Например, сверхпроводимость (superconductivity), сверхтекучесть (superfluid), переохлаждение (supercooling), перенасыщение (supersaturation). Сверхпроводящий суперколлайдер (ССК) должен был стать самым мощным в мире, если бы Конгресс США не зарубил проект в 1993 году, и т. д., список можно продолжить. Поэтому вы можете представить воодушевление физиков, когда они обнаружили, что пространственно-временная симметрия обладает большей, «супер-», симметрией.
Открытие суперсимметрии было поистине удивительным событием. К моменту возникновения суперсимметричных теорий физики считали, что им известны все симметрии пространства и времени. Как мы видели в гл. 9, уже привычными симметриями были пространственно-временные, утверждавшие, что исходя только из законов физики невозможно определить, где вы находитесь, в какую сторону смотрите или какое сейчас время. Действительно, траектория баскетбольного мяча не зависит от того, на какой стороне площадки вы находитесь, и где происходит игра — в Калифорнии или Нью-Йорке.
В 1905 году, с появлением теории относительности, список преобразований пространственно-временных симметрий расширился, включив те преобразования, которые изменяют вектор-скорость (величину скорости и направление движения), и ученые полагали, что этим список исчерпывается. Никто не верил, что могут быть еще какие-то неоткрытые симметрии, включающие пространство и время. Два физика, Джеффри Мандула и Сидни Коулмен, в 1967 году закрепили это интуитивное утверждение, доказав, что не существует других подобных симметрий. Однако они (и все остальные) проглядели одну возможность, основанную на нетрадиционных предположениях.
В этой главе вводится понятие суперсимметрии — странного нового преобразования симметрии, переставляющего бозоны и фермионы. С его помощью можно строить теории, включающие преобразования суперсимметрии. Однако суперсимметрия как симметрия природы все еще остается гипотетической, так как никто еще не обнаружил суперсимметрию в окружающем нас мире. Тем не менее есть две весомых причины, позволяющие физикам думать, что эта симметрия существует в природе.
Одна причина — это понятие суперструны, которое будет подробнее рассмотрено в следующей главе. Теория суперструн, включающая суперсимметрию, является единственной известной моделью теории струн, способной воспроизвести частицы Стандартной модели. Теория струн без суперсимметрии не может претендовать на описание нашей Вселенной.
Вторая причина состоит в том, что суперсимметричные теории обладают потенциальными возможностями решить проблему иерархии. Суперсимметрия не объясняет причину большого отношения масштаба массы слабых взаимодействий к планковскому масштабу масс, но она исключает проблематичные огромные квантовые вклады в массу хиггсовского бозона. Вопрос иерархии является серьезной проблемой и очень мало предложенных решений выжили после тщательной экспериментальной и теоретической проверки. До того момента, как в качестве потенциальной альтернативы были предложены теории с дополнительными измерениями, суперсимметрия была единственным решением проблемы.
Так как мы до сих пор не знаем, существует ли суперсимметрия во внешнем мире, все, что мы можем сделать, — это рассмотреть предлагаемые теоретические варианты и оценить их следствия. При таком подходе, к моменту, когда эксперименты достигнут области более высоких энергий, мы будем готовы описать, что собой представляет та теория, которая лежит в основе Стандартной модели. Поэтому посмотрим, чем мы располагаем.
Фермионы и бозоны: невероятная пара
В суперсимметричном мире каждой известной частице соответствует другая частица — суперсимметричный партнер или, как говорят, суперпартнер, в которого она превращается в результате преобразования суперсимметрии. Преобразование суперсимметрии превращает фермион в его партнера — бозон, а бозон — в партнера-фермион. В гл. 6 мы видели, что фермионы и бозоны — это разные типы частиц квантово-механических теорий, отличающиеся значением спина. Спин фермионнных частиц полуцелый, а бозонных — целый. Целые значения спина — это те числа, которыми можно характеризовать обычные тела, вращающиеся в пространстве, в то время как полуцелые значения являются специфическим понятием квантовой механики.
В суперсимметричной теории все фермионы могут превращаться в соответствующие бозоны, а все бозоны — в соответствующие фермионы. Суперсимметрия — это прием теоретического описания таких частиц. И если вы анализируете уравнения, описывающие поведение частиц в результате преобразования суперсимметрии, переставляющего бозоны и фермионы, то эти уравнения после преобразования должны выглядеть аналогично. Все предсказания должны быть тождественны тем, которые можно было сделать до преобразования симметрии.
На первый взгляд, рассматриваемая нами симметрия игнорирует логику. Предполагается, что преобразования симметрии оставляют систему неизменной, однако преобразования суперсимметрии меняют местами частицы, которые существенно различны — фермионы и бозоны.
И хотя было странно предположить, что за преобразованием, смешивающим столь разные объекты, может скрываться симметрия, тем не менее ряд физиков рассмотрели такую возможность. В 1970-е годы европейские и советские физики[127] показали, что симметрия может переставлять местами столь различные частицы и законы физики могут при этом оставаться неизменными.
Эта симметрия несколько отличается от предыдущих, так как подвергающиеся перестановкам объекты явно обладают разными свойствами. Тем не менее симметрия может существовать, если бозоны и фермионы присутствуют в равных количествах. В качестве аналогии рассмотрим два набора красных и зеленых шариков разных размеров, причем наборы отличаются только цветом. Допустим, вы сели играть в шарики с приятелем. Вы играете красными шариками, а ваш приятель — зелеными. Если у каждого красного шарика имеется единственная пара среди зеленых шариков, то не важно, каким цветом вы играете — вы не получите никаких преимуществ в игре. Однако, если количества красных и зеленых шариков каждого размера не равны друг другу, игроки будут поставлены в неравные условия. Начальный выбор красного или зеленого цвета будет иметь значение и игра будет происходить по-другому, если вы со своим приятелем поменяетесь цветами. Чтобы была симметрия, шарики каждого размера должны быть двух цветов — красного и зеленого, и должно быть одинаковое число шариков каждого цвета и каждого размера.
Аналогично, суперсимметрия возможна только при условии, что бозоны и фермионы точно объединяются в пары. Вам необходимо иметь равное число бозонных и фермионных типов частиц. И точно так же, как шарики, меняющиеся местами, должны иметь одинаковые размеры, спаренные бозоны и фермионы должны иметь одинаковые массу и заряды, а их взаимодействия должны контролироваться одинаковыми параметрами. Иными словами, каждая частица должна иметь своего суперпартнера с аналогичными свойствами. Если бозон испытывает сильные взаимодействия, эти же взаимодействия испытывает его суперсимметричный партнер. Если имеются взаимодействия, включающие определенные частицы, то должны быть и связанные с ними взаимодействия, включающие их суперсимметричных партнеров.
Одна из причин, которая делает суперсимметрию столь интригиующей, состоит в том, что если она будет открыта в нашем мире, это будет первая новая пространственно-временная симметрия, найденная за последние сто лет. Именно поэтому она — «супер». Я не стану углубляться в математические объяснения, но только знания того, что суперсимметрия переставляет частицы с разным спином, достаточно для понимания этого факта. Так как спины частиц различны, бозоны и фермионы преобразуются по-разному при вращениях в пространстве, поэтому для компенсации этой разницы в преобразования суперсимметрии должны входить пространство и время.
Но не подумайте, что это означает, что вы сможете представить, как выглядит отдельное преобразование суперсимметрии в физическом пространстве. Даже физики понимают суперсимметрию только в терминах ее математического описания и экспериментальных следствий. А последние, как мы скоро увидим, очень впечатляют.
Суперистория
Этот раздел можно, в принципе, пропустить. Он носит исторический характер и в нем не вводится никаких новых понятий, существенных для дальнейшего изложения. Но история развития теории суперсимметрии интересна потому, что она демонстрирует плодотворность новых идей и путь, на котором теория струн и построение моделей иногда образуют продуктивный симбиоз. Теория струн послужила толчком для поиска суперсимметрии, теория суперструн — наилучший возможный вариант теории струн для описания реального мира — родилась только благодаря идеям, пришедшим из супергравитации, т. е. суперсимметричной теории, включающей гравитацию.
Пьер Рамон, физик французского происхождения, в 1971 году предложил первую суперсимметричную теорию. Он рассматривал не четыре измерения, в которых (как мы привыкли думать) мы живем, а два — одно пространственное и одно временное. Цель Рамона состояла в том, чтобы найти способ включения фермионов в теорию струн. По техническим причинам, первоначальная версия теории струн включала только бозоны, однако в любой теории, которая надеется описать наш мир, без фермионов не обойтись.
Теория Рамона содержала двумерную суперсимметрию и превратилась в теорию фермионных струн, построенную им совместно с Андре Невье и Джоном Шварцем. Теория Рамона была первой суперсимметричной теорией, появившейся в западном мире; одновременно суперсимметрию открыли Гольфанд и Лихтман в Советском Союзе, но их работы были спрятаны от Запада за железным занавесом.
Так как четырехмерная квантовая теория поля опиралась на значительно более солидное основание, чем теория струн, возник очевидный вопрос: возможна ли суперсимметрия в четырех измерениях? Однако, поскольку суперсимметрия сплетена со структурой пространства-времени, обобщить ее двумерный вариант на случай четырех измерений оказалось непростой задачей. В 1973 году немецкий физик Юлиус Весс и уроженец Италии физик Бруно Зумино построили четырехмерную суперсимметричную теорию. Независимо, в Советском Союзе Дмитрий Волков и Владимир Акулов построили другую четырехмерную суперсимметричную теорию, но холодная война снова воспрепятствовала обмену идеями.
С развитием четырехмерной суперсимметричной теории, все большее количество физиков обращало на нее внимание. Однако модель Весса — Зумино 1973 года не могла включить все частицы Стандартной модели; никто не знал, как добавить в четырехмерную суперсимметричную теорию переносящие взаимодействия калибровочные бозоны. В 1974 году эту трудную задачу решили итальянские теоретики Сержио Феррара и Бруно Зумино.
Возвращаясь с конференции «Струны-2002», по пути из Кембриджа в Лондон, Сержио рассказал мне, почему поиск правильной теории был бы немыслимо трудной задачей, если бы не использование формализма суперпространства — абстрактного расширения пространства-времени, имеющего дополнительные фермионные измерения. Суперпространство — необычайно сложное понятие, и я не буду даже пытаться его объяснить. Важно то, что этот совершенно новый тип измерения, не похожий на привычные пространственные измерения, играет ключевую роль в становлении суперсимметрии. Этот чисто теоретический инструмент продолжает и сегодня упрощать расчеты суперсимметрии.
Теория Феррары — Зумино показала физикам, как включить в суперсимметричную теорию электромагнетизм, слабые и сильные взаимодействия. Однако суперсимметричные теории все еще не включали гравитацию. Поэтому в суперсимметричной теории мира оставался открытым вопрос, может ли она включить это остающееся взаимодействие. В 1976 году три физика, Сержио Феррара, Дэн Фридман и Питер ван Нивенхойзен решили эту задачу, построив теорию супергравитации — сложную суперсимметричную теорию, включающую гравитацию и теорию относительности.
Любопытно, что пока формулировалась теория супергравитации, независимо развивалась и теория струн. В одной из ключевых теоретических работ по теории струн Фердинандо Льоцци, Джоэл Шерк и Дэвид Олив обнаружили стабильную модель, являющуюся результатом развития теории фермионных струн Рамона, Невье и Шварца. Оказалось, что теория фермионных струн содержит тип частиц, с которыми никто ранее не сталкивался нигде, кроме теорий супергравитации. Свойства новой частицы были тождественны свойствам суперсимметричного партнера гравитона, получившего имя гравитино, и в действительности им она и оказалась.
Параллельно шло развитие и супергравитации, поэтому физики ухватились за этот общий элемент двух теорий и, работая над ним, вскоре осознали, что суперсимметрия присутствует в теории фермионных струн. В этот момент родилась теория суперструн.
В следующей главе мы вернемся к теории струн и теории суперструн. Сейчас же мы сосредоточимся на другом важном приложении суперсимметриии — ее следствиях, касающихся физики частиц и проблемы иерархии.
Суперсимметричное расширение Стандартной модели
Суперсимметрия станет самой строгой и изящной теорией, если объединит в пары все известные частицы. Но чтобы это случилось, Стандартная модель должна содержать равное число фермионов и бозонов, однако она не удовлетворяет этому критерию. Отсюда вытекает, что если наша Вселенная суперсимметрична, она должна содержать много новых частиц. На самом деле она должна содержать по меньшей мере вдвое большее число частиц, чем до сих пор наблюдали экспериментаторы. Все фермионы Стандартной модели — три поколения кварков и лептонов — должны быть объединены в пары с новыми, до сих пор неоткрытыми суперпартнерами-бозонами. Калибровочные бозоны — частицы, переносящие взаимодействия, — должны также иметь суперпартнеров.
В суперсимметричной Вселенной партнерами кварков и лептонов будут новые бозоны. Физики, забавляющиеся причудливой (но систематичной) терминологией, назвали их скварками и слептонами. В общем случае, бозонный супер-симметричный партнер фермиона имеет то же имя, что и фермион, но с буквой «с» в начале. Например, электроны спариваются с сэлектронами, а топ-кварки со стоп-скварками. У каждого фермиона есть свой бозонный суперпартнер — соответствующий ему сфермион.
Свойства этих частиц и их суперпартнеров строго подлажены друг к другу: бозонные суперпартнеры имеют такие же массы, заряды и взаимодействия, как и их фермионные партнеры. Например, если электрон имеет заряд -1, такой же заряд имеет и сэлектрон; если нейтрино участвует в слабом взаимодействии, так же взаимодействует и снейтрино.
Если Вселенная суперсимметрична, у бозонов также должны быть суперпартнеры. Известными бозонами Стандартной модели являются переносчики взаимодействий: фотон, заряженные W-бозоны, нейтральный Z-бозон и глюоны, причем спин всех этих частиц равен 1. Терминология суперсимметрии требует, чтобы новые фермионные суперпартнеры имели бы то же имя, что и бозон, с которым они образуют пару, с добавлением в конце суффикса «-ино». Так, фермионные партнеры калибровочных бозонов W и Z называются вино и зино, фермионные партнеры глюонов называются глюино, а фермионный партнер хиггсовской частицы называется хиггсино. Так же как и бозонные суперпартнеры, фермионные суперпартнеры имеют те же заряды, те же взаимодействия и — если суперсимметрия является точной — ту же массу, что и бозоны, с которыми они спарены (рис. 64).

Вам может показаться странным, что физики настолько серьезно воспринимают возможность существования суперсимметрии, если учесть, что ни один суперпартнер не был когда-либо обнаружен, меня иногда поражает, насколько часть моих коллег верят в это. Но, даже несмотря на то, что суперсимметрия до сих пор не обнаружена в природе, есть ряд причин, позволяющих подозревать ее наличие. Серджио Феррара, один из первых ученых, работавших над теорией суперсимметрии, выразил мнение многих физиков, когда сказал мне во время нашей поездки в Лондон, что было бы трудно поверить, что такая удивительная и восхитительная теоретическая конструкция не играет никакой роли в устройстве мира.
Другие физики, не так легко поддающиеся очарованию симметрии, верят в суперсимметрию прежде всего из-за преимуществ суперсимметричных расширений Стандартной модели. В противоположность несуперсимметричным теориям, эти расширения поддерживают легкую хиггсовскую частицу и иерархию масс.
Суперсимметрия и проблема иерархии
Проблема иерархии в Стандартной модели сводится к вопросу о том, почему хиггсовская частица такая легкая. Каким образом может существовать легкая хиггсовская частица при больших квантовых вкладах в ее массу от виртуальных частиц? Эти большие вклады показывают, что в Стандартной модели присутствует обманчивый трюк.
Большое преимущество суперсимметричного расширения Стандартной модели состоит в том, что если имеются виртуальные вклады как от частиц, так и от их суперпартнеров, то суперсимметрия гарантирует отсутствие больших квантовых вкладов в массу хиггсовской частицы, из-за которых легкая хиггсовская частица выглядит столь неправдоподобной. В суперсимметричных теориях могут быть только такие взаимодействия, в которых бозонные и фермионные взаимодействия скоррелированы. Благодаря накладываемым этим условием ограничениям, в суперсимметричных теориях не возникает проблем с большими квантовыми поправками к массам частиц.
В суперсимметричной теории виртуальные частицы Стандартной модели являются не единственными виртуальными частицами, вносящими вклад в массу хиггсовской частицы, другой вклад вносят виртуальные суперпартнеры. Из-за удивительных свойств суперсимметрии два типа вкладов всегда дают в сумме нуль. Квантовые вклады виртуальных фермионов и бозонов в массу хиггсовской частицы связаны друг с другом так точно, что большие вклады от фермионов и бозонов гарантированно сокращаются. Значение фермионного вклада отрицательно и в точности уничтожает вклад бозонов.
Одно такое сокращение показано на рис. 65, на котором показаны две диаграммы, одна с виртуальным топ-кварком, а другая — с виртуальным стоп-скварком. Каждая из диаграмм в отдельности приводила бы к большому вкладу в массу хиггсовской частицы. Но из-за особой взаимосвязи между частицами и взаимодействиями в суперсимметричных теориях большие квантовые вклады в массу от топ-кварков и стоп-скварков полностью уничтожаются, так как их сумма равна нулю.
В несуперсимметричной теории огромные квантовые вклады в массу хиггсовской частицы разрушили бы низкоэнергетическое нарушение электрослабой симметрии, если только в результате ловкого трюка все большие вклады в массу частицы не дали бы в сумме очень маленькое число. Однако суперсимметричное расширение Стандартной модели гарантирует, что всякие потенциально дестабилизирующие влияния типа показанных на этих диаграммах дадут в сумме нуль. Малое значение классической массы хиггсовской частицы гарантирует, что истинная масса, включающая квантовые вклады, также будет малой.

Суперсимметрия представляется как гибкое, прочное основание Стандартной модели. Если раньше мы говорили, что тонкая настройка Стандартной модели похожа на балансировку, чтобы удерживать карандаш на острие, то суперсимметрия похожа на тонкую проволочку, удерживающую карандаш на месте. Аналогично, если ранее мы думали о проблеме иерархии как о сотрудниках Службы иммиграции и натурализации, превышающих свои полномочия и задерживающих слишком большое количество обращений, суперсимметричные партнеры похожи на правозащитников, пресекающих нарушения сотрудников иммиграционной службы и позволяющих большинству обращений дойти до места.
Так как вклады обычных виртуальных частиц вместе с вкладами их суперсимметричных партнеров дают в сумме нуль, суперсимметрия гарантирует, что квантово-механические вклады от виртуальных частиц не исключают возможность существования частиц малой массы. В суперсимметричной теории частица, которая предполагается легкой, например хиггсовская частица, будет оставаться легкой, даже если мы учтем виртуальные вклады.
Нарушенная суперсимметрия
Хотя суперсимметрия в принципе решает проблемы больших виртуальных вкладов в массу хиггсовской частицы, в ней существует серьезная проблема, о которой я пока что не упоминала. Мир очевидно несуперсимметричен. Откуда это следует? Если бы существовали суперпартнеры известных частиц с такими же массами и зарядами, мы бы их давно уже наблюдали. Однако никто еще не наблюдал сэлектрона или фотино.
Из этого не следует, что мы должны отвергнуть идею суперсимметрии. Но это означает, что суперсимметрия, если она существует в природе, не может быть точной симметрией. Как и локальная симметрия, сопровождающая электрослабое взаимодействие, суперсимметрия должна быть нарушенной.
Теоретические рассуждения показывают, что суперсимметрия может быть нарушена, если частицы и их суперпартнеры имеют различные массы; эти массы становятся различными благодаря малым эффектам нарушения суперсимметрии. Разность масс частиц и соответствующих суперпартнеров будет контролироваться степенью нарушения суперсимметрии. Если суперсимметрия нарушена мало, разность масс будет малой, если же нарушение сильное, разность масс будет большой. В действительности разность масс частиц и их суперпартнеров — один из способов описания того, насколько сильно нарушена суперсимметрия.
Почти во всех моделях нарушения суперсимметрии массы суперпартнеров больше, чем массы известных частиц. Это счастливое обстоятельство, так как тот факт, что суперпартнеры тяжелее своих партнеров из Стандартной модели, критически важен для согласования суперсимметрии с экспериментальными наблюдениями. Это могло бы объяснить, почему мы до сих пор их не наблюдаем. Более тяжелые частицы могут рождаться только при больших энергиях, и если суперсимметрия существует, коллайдеры просто не достигли высоких энергий, достаточных для рождения таких частиц. Поскольку в экспериментах исследованы энергии вплоть до нескольких сотен ГэВ и суперпартнеры до сих пор не найдены, следовательно, если они существуют, их массы должны быть не меньше этого предела.
Конкретное значение массы, которую должен иметь суперпартнер, чтобы избежать обнаружения, зависит от конкретного заряда и типа взаимодействия этой частицы. Чем сильнее взаимодействия, тем легче рождаются частицы. Таким образом, чтобы избежать обнаружения, частицы с более сильными взаимодействиями должны быть тяжелее, чем слабо взаимодействующие частицы. Современные экспериментальные ограничения на большинство моделей нарушения суперсимметрии говорят о том, что если суперсимметрия существует, то для того, чтобы избежать обнаружения, все суперпартнеры должны иметь массы не менее нескольких сотен ГэВ. Те суперпартнеры, которые испытывают сильное взаимодействие, такие как скварки, должны быть еще тяжелее, с массами не менее тысячи ГэВ.
Нарушенная суперсимметрия и масса хиггсовской частицы
Как мы видели, квантовые вклады в массу хиггсовской частицы не создают проблем в суперсимметричных теориях, так как суперсимметрия гарантирует, что сумма этих вкладов равна нулю. Однако мы только что показали, что для того, чтобы существовать в реальном мире, суперсимметрия должна быть нарушенной. Так как в модели с нарушенной суперсимметрией массы суперпартнеров отличаются от масс их партнеров в Стандартной модели, квантовые вклады в массу хиггсовской частицы не столь жестко сбалансированы, как в случае, когда суперсимметрия является точной. Таким образом, когда суперсимметрия нарушена, уже не происходит точного сокращения виртуальных вкладов.
Тем не менее пока квантовые вклады в массу хиггсовской частицы не слишком велики, Стандартная модель годится и без тонкой настройки или подгонки. Даже в случае, когда суперсимметрия нарушена, до тех пор пока эффект мал, Стандартная модель может включать легкую хиггсовскую частицу. Если суперсимметрия немного нарушена, она все же достаточно сильна для того, чтобы исключить огромные вклады планковского масштаба масс от виртуальных энергичных частиц. Всего лишь при малой величине нарушения суперсимметрии особо нежелательных сокращений не потребуется.
Мы хотим, чтобы нарушение суперсимметрии было достаточно мало, что позволяет сделать нарушающую суперсимметрию разность масс между частицами Стандартной модели и их суперпартнерами достаточно малой для того, чтобы избежать подгонки. Оказывается, что хотя квантовый вклад в массу хиггсовской частицы от виртуальной частицы и ее суперпартнера не равен нулю, он никогда не достигает величины, много большей, чем нарушающая суперсимметрию разность масс между частицей и ее суперпартнером. Отсюда следует, что разность масс между всеми частицами и их суперпартнерами должна быть порядка масштаба массы слабых взаимодействий. В этом случае квантовые вклады в массу хиггсовской частицы также будут порядка слабой шкалы масс, что дает примерно правильную величину массы хиггсовской частицы.
Так как известные частицы в Стандартной модели легкие, разность масс между частицей Стандартной модели и ее суперпартнером будет сравнимой с массой суперпартнера. Поэтому, если суперсимметрия решает проблему иерархии, массы суперпартнеров не должны быть многим больше, чем масштаб массы слабых взаимодействий порядка 250 ГэВ.
Если массы суперпартнеров того же порядка, что и масштаб массы слабых взаимодействий, квантовый вклад в массу хиггсовской частицы не должен быть очень большим. В противоположность несуперсимметричному случаю, когда квантовые вклады в массу хиггсовской частицы на шестнадцать порядков величины больше, чем нужно, так что требуется неприемлемая подгонка, чтобы получить легкую хиггсовскую частицу, суперсимметричный мир с нарушающими суперсимметрию массами в несколько сотен ГэВ не породит слишком больших квантовых вкладов в массу хиггсовской частицы.
Требование, чтобы хиггсовская частица, а следовательно, и суперпартнеры, были бы ненамного тяжелее нескольких сотен ГэВ (так, чтобы не вносить большие квантовые вклады в массу хиггсовской частицы), вместе с тем фактом, что эксперименты уже осуществили поиск суперпартнеров с массами порядка пары сотен ГэВ, говорит о том, что если суперсимметрия существует в природе и решает проблему иерархии, то суперсимметричные партнеры должны иметь массы порядка нескольких сотен ГэВ. Это очень волнующее утверждение, так как оно подразумевает, что экспериментальное свидетельство существования суперсимметрии может быть совсем рядом, за углом, и совсем скоро может быть получено на коллайдерах частиц. Совсем небольшое увеличение энергии по сравнению с существующим коллайдером Тэватроном может оказаться достаточным, чтобы достичь энергий, при которых должны появиться суперпартнеры.
Эту область энергий будет изучать Большой адронный коллайдер. Если суперсимметрия не будет открыта на БАК, который будет искать частицы с массами до нескольких тысяч ГэВ, это будет означать, что суперпартнеры слишком тяжелы, чтобы решить проблему иерархии, и суперсимметричное решение будет исключено.
Но если суперсимметрия решает проблему иерархий, это будет экспериментальный шквал. Ускоритель частиц с энергиями порядка 1 ТэВ (1000 ГэВ) обнаружит вдобавок к хиггсовской частице еще кучу суперсимметричных партнеров частиц Стандартной модели. Мы увидим глюино и скварки, а также слептоны, вино, зино и фотино. Все новые частицы будут иметь те же заряды, что и частицы Стандартной модели, но будут тяжелее. При достаточной энергии соударений эти частицы будет трудно пропустить. Если суперсимметрия верна, мы скоро получим подтверждение этого.
Суперсимметрия: оценка доказательств
Это ставит нас перед главнейшим вопросом: существует ли суперсимметрия в природе? Жюри еще не вынесло вердикт. Без дополнительных фактов любой ответ будет только предположением. В настоящее время как защита, так и обвинение имеют аргументы в свою пользу.
Уже отмечались две важнейшие причины верить в суперсимметрию: проблема иерархии и суперструны. Третий убедительный довод в пользу суперсимметрии — потенциальная возможность объединения всех взаимодействий в супер-симметричных расширениях Стандартной модели. Как обсуждалось в гл. 11, константы электромагнитных, слабых и сильных взаимодействий зависят от энергии. Хотя первоначально Джорджи и Глэшоу обнаружили, что взаимодействия в Стандартной модели объединяются, более точные измерения этих трех взаимодействий показали, что объединение в Стандартной модели происходит не полностью. На верхнем чертеже рис. 66 представлены графики трех констант взаимодействий как функций энергии.
Однако суперсимметрия вводит много новых частиц, обладающих этими же тремя взаимодействиями. Это приводит к изменению зависимости взаимодействий от расстояния (или энергии), так как среди виртуальных частиц теперь присутствуют и суперсимметричные партнеры. Возникающие дополнительные квантовые вклады входят в расчеты методом ренормализационной группы и влияют на то, как зависят от энергии константы электромагнитных, слабых и сильных взаимодействий.
Нижний график на рис. 66 показывает, каким образом константы взаимодействий зависят от энергии, если учесть влияние суперпартнеров. Примечательно, что с учетом суперсимметрии три взаимодействия объединяются точнее, чем до этого. Это более важно сейчас, чем в ранних попытках объединения, так как теперь в нашем распоряжении имеются значительно более точные измерения констант взаимодействий. Пересечение трех линий может быть случайностью. Но оно может рассматриваться и как свидетельство в поддержку суперсимметрии.
Другое приятное свойство суперсимметричных теорий состоит в том, что они содержат естественного кандидата на роль темной материи. Темная материя — это несветящаяся материя, заполняющая Вселенную, которая была обнаружена по своему гравитационному притяжению. Даже несмотря на то что четверть энергии Вселенной запасено в темной материи, мы до сих пор не знаем, из чего эта материя состоит[128]. Подходящим кандидатом на роль темной материи могла бы быть суперсимметричная частица, которая не распадается и имеет подходящую массу и константу взаимодействия. Действительно, легчайшая суперсимметричная частица не распадается и могла бы иметь нужную массу и нужные взаимодействия, чтобы быть той частицей, из которых состоит темная материя. Таким наилегчайшим суперпартнером может быть фотино, партнер фотона. Другой вариант — в сценарии с дополнительными измерениями, который мы рассмотрим ниже, такой частицей может быть вино, партнер калибровочного W-бозона.
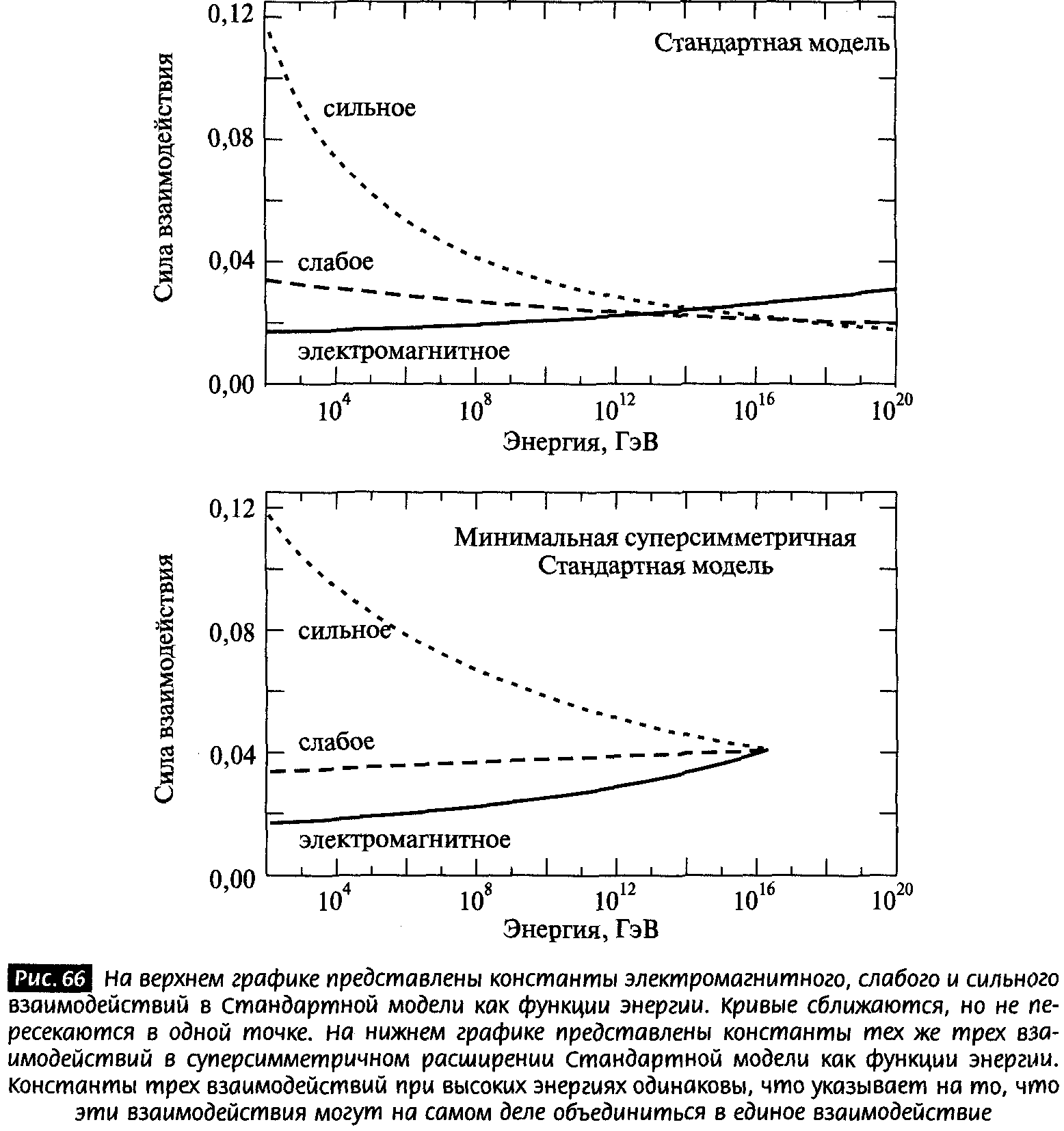
Однако доводы в пользу суперсимметрии не единственно возможные. Сильнейшим аргументом против суперсимметрии является то, что ни хиггсовская частица, ни ее суперсимметричные партнеры до сих пор не найдены. Экспериментаторы достигли энергий в несколько сотен ГэВ. Хотя суперпартнеры, безусловно, могут быть чуть тяжелее, на самом деле для этого нет никаких причин. Более легкие суперпартнеры даже лучше с точки зрения решения проблемы иерархии. Почему же, если суперсимметрия решает проблему иерархии, суперпартнеры еще не обнаружены?
С теоретической точки зрения суперсимметрия не полностью неопровержима, так как остаются серьезные вопросы по поводу того, как она нарушается. Мы знаем, что она должна быть нарушена спонтанно, но, как и в случае Стандартной модели и симметрии слабых взаимодействий, мы до сих пор не знаем, какие частицы ответственны за это нарушение. Было предложено много блестящих идей, но полностью удовлетворительная четырехмерная теория еще не предложена.
Когда я впервые узнала о суперсимметрии, она показалась мне слишком простой с точки зрения построения моделей. Дело выглядело так, как будто суперсимметричные теории могли содержать случайные несвязанные массы, так как квантовые вклады отсутствовали. И хотя мы не знали, почему должны появляться неравноправные массы, они не причиняли никаких неприятностей. Это было очень досадно с точки зрения построения моделей, так как ничто не давало никакого ключа к до сих пор не определенной базисной теории. Кроме того, это было немного скучно, так как казалось, что моделирование не является слишком сложной задачей.
Но затем я узнала о проблеме аромата в суперсимметричных теориях, из которой следует, что не все так просто; на самом деле очень трудно установить конкретные детали теории при наличии нарушенной суперсимметрии. Проблема является довольно тонкой, но тем не менее она важна. Проблема аромата есть главное препятствие к построению простой теории нарушения суперсимметрии. Все новые теории нарушения суперсимметрии концентрируются на этой проблеме, и в гл. 17 будет показано, почему возможным решением является нарушение суперсимметрии в дополнительных измерениях.
Напомним, что ароматы фермионов Стандартной модели — это три различных фермиона трех разных поколений, имеющих одинаковые заряды, но разные массы, например, кварки и, cиt, или электрон, мюон и тау. В Стандартной модели ароматы лептонов не меняются. Например, мюоны никогда непосредственно не взаимодействуют с электронами, они взаимодействуют только косвенно, через обмен слабым калибровочным бозоном. Хотя мюоны могут распадаться в электроны, это происходит только потому, что среди продуктов распада имеются также мюонное нейтрино и электронное антинейтрино (см. рис. 53 на стр. 151). Мюон никогда не превращается непосредственно в электрон без испускания соответствующих нейтрино.
Способ, которым физики фиксируют эту индивидуальность конкретного типа лептонов, состоит в том, чтобы потребовать сохранения электронного или мюонного числа. Мы приписываем положительное электронное число электрону и электронному нейтрино, и отрицательное электронное число — позитрону и антинейтрино. Аналогично, мы приписываем положительное мюонное число мюону и мюонному нейтрино, и отрицательное мюонное число — антимюону и мюонному антинейтрино. Если мюонное и электронное числа сохраняются, мюон никогда не сможет распасться на электрон и фотон, так как в начале у нас есть положительное мюонное число и нулевое электронное число, а в конце — нулевое мюонное число и положительное электронное число. Действительно, никто никогда не наблюдал подобного распада. Насколько мы знаем, электронное и мюонное числа сохраняются всеми взаимодействиями частиц.
В суперсимметричной теории сохранение электронного и мюонного чисел говорило бы нам, что хотя электрон и сэлектрон могут взаимодействовать через слабое взаимодействие, как это могут делать мюон и смюон, электрон никогда не может непосредственно взаимодействовать со смюоном. Если бы по какой-то причине электрон был спарен со смюоном, или мюон — с сэлектроном, то возникли бы взаимодействия, не наблюдаемые в природе, например распад мюона на электрон и фотон.
Проблема состоит в том, что хотя в строго суперсимметричной теории такие меняющие аромат взаимодействия не возникают, как только суперсимметрия нарушается, ничто не гарантирует нам, что мюонное и электронное числа сохраняются. Суперсимметричные взаимодействия в теории с нарушенной суперсимметрией могут изменять число электронов и мюонов, в противоречии с тем, что мы знаем из опыта. Происходит это потому, что массивные бозонные суперпартнеры в строгом смысле не тождественны своим партнерам фермионам. Массы, которыми они обладают в суперсимметричной теории, позволяют бозонным суперпартнерам полностью перемешиваться. Например, с мюоном может быть спарен не только смюон, но и сэлектрон. Но спаривание сэлектрона с мюоном приведет ко всем типам распадов, которые, как мы знаем, не происходят. В любой правильной теории природы взаимодействия, изменяющие мюонное или электронное числа, должны быть очень слабыми (или несуществующими), так как такие взаимодействия никогда не наблюдались.
У кварков возникнут похожие проблемы. Если суперсимметрия нарушена, то кварковый аромат не только не будет сохраняться, но будет приводить к опасному перемешиванию поколений, чего так боялся Икар в начале главы. Определенное смешивание кварков в природе происходит, но оно существенно меньше, чем предсказывается теориями с нарушением суперсимметрии.
Теории с нарушением суперсимметрии сталкиваются с очень трудной проблемой объяснения того, почему подобные меняющие аромат взаимодействия не встречаются намного чаще. К сожалению для суперсимметричных теорий, большинство их не может объяснить отсутствие явлений с изменением аромата, подобных упомянутым выше. Это недопустимо; такое смешивание должно быть запрещено, если теории соответствую природе.
Если эта проблема кажется вам неясной, возможно, вам принесет облегчение тот факт, что многие физики первоначально чувствовали то же самое и не считали проблему ароматов в суперсимметричных теориях столь важной. Если до предела упростить проблему, раскол в мыслях проходил вдоль географических границ: европейцы тревожились по поводу этой проблемы меньше американцев. Те из нас, кто уже потратил годы на обдумывание проблемы аромата с иных точек зрения, знали, как трудно было бы ее решить. Но многие изначально игнорировали следствия анархического принципа и не видели, почему надо тревожиться. Однажды, после возвращения в 1994 году с Международной конференции по суперсимметрии в Анн-Арборе, штат Мичиган, Дэвид Каплан, прекрасный физик (и мой первый коллега во время аспирантуры), работающий сейчас в Институте ядерной физики в Сиэттле, рассказал мне, как он был расстроен после того, как объяснил аудитории предлагаемое им решение проблемы аромата, но только потом обнаружил, как мало людей думали, что там вообще была проблема!
Однако все довольно быстро изменилось. Большинство ученых сейчас признает серьезность проблемы ароматов. Очень трудно найти теории нарушения суперсимметрии, которые выдают все необходимые массы суперпартнеров, не подвергая опасности ароматы частиц. Как нарушить суперсимметрию, но не допустить изменения аромата, — это ключевая проблема, если суперсимметрия преуспеет в решении проблемы иерархии. Нарушение законов сохранения числа мюонов и электронов (а также кварков) может показаться технической проблемой, но на самом деле это ахиллесова пята нарушения суперсимметрии. Очень трудно предотвратить превращение суперпартнеров друг в друга. В общем случае симметрии бессильны это предотвратить.
И вновь мы возвращаемся к нашей теме: теории с симметрией элегантны, но нарушенная симметрия, описывающая видимый нами мир, должна быть в равной степени элегантна. Как и почему нарушается суперсимметрия? Мы завершим сложную теоретическую задачу понимания суперсимметричных теорий только тогда, когда мы найдем убедительную модель нарушения суперсимметрии.
Это не означает, что суперсимметрия с необходимостью неверна, или что она не имеет ничего общего с проблемой иерархии. Однако требуется дополнительный ингредиент для того, чтобы суперсимметричные теории мира были успешными. Вскоре мы увидим, что таким дополнительным ингредиентом могут быть дополнительные измерения.
Что стоит запомнить
• Суперсимметрия по существу удваивает спектр частиц. Для каждого бозона, имеющегося в теории, суперсимметрия вводит партнера — фермион, для каждого фермиона вводит партнера — бозон.
• Квантово-механические эффекты (без суперсимметрии) приводят к тому, что хиггсовская частица не может остаться достаточно легкой, как это требуется в Стандартной модели. До появления теорий с дополнительными измерениями, суперсимметрия была единственным известным способом борьбы с этой проблемой.
• Суперсимметрия не обязательно объясняет нам, почему хиггсовская частица легкая, но она решает проблему иерархий.
• Большие виртуальные вклады, которые вносят в массу хиггсовской частицы все частицы Стандартной модели и их суперпартнеры, при суммировании дают нуль. Поэтому наличие легкой хиггсовской частицы не является проблемой для суперсимметричнной теории.
• Даже несмотря на то что суперсимметрия могла бы решить проблему иерархий, она не может быть точной. Если бы она была точной, суперпартнеры имели бы те же массы, что и частицы Стандартной модели, и мы должны были бы уже найти экспериментальные следствия суперсимметрии.
• Суперпартнеры, если они существуют, должны быть массивнее, чем их партнеры в Стандартной модели. Так как на коллайдерах высоких энергий могут рождаться только частицы, массы которых не превышают некоторого предела, эти коллайдеры еще не имеют достаточную энергию, чтобы породить суперчастицы. Это может объяснить, почему мы до сих пор их не видели.
• Если суперсимметрия нарушена, могут возникать меняющие аромат взаимодействия. Это процессы, в которых кварки или лептоны превращаются в кварки и лептоны другого поколения (т. е. более тяжелые или более легкие) с теми же зарядами. Это очень странные процессы — они меняют индивидуальность известных частиц и встречаются в природе очень редко. Но большинство теорий нарушенной суперсимметрии предсказывают, что они должны возникать очень часто, намного чаще, чем это наблюдается на опыте.
IV Теория струн и браны
Глава 14
Allegro (mа non troppo) Пассаж для струнных
I’ve got the world on a string.
Frank Sinatra[129]
Прокрутим пленку вперед на миллион лет.
Икар Рашмор XLII занимался испытаниями своей новой машины Алисэксвир (Alicxvr) модели 6.3, которую он недавно приобрел по Спейснету. (Интерес Икара III к скорости и всяким техническим новинкам, по-видимому, передался через многие поколения.) Алисэксвир был сконструирован так, чтобы дать возможность пользователю увидеть вещи любого размера, от самых маленьких до очень больших. Икар был совершенно уверен, что все его друзья, приобретшие Алисэксвир, сначала попробуют испытать действие установки для больших расстояний во много мегапарсеков, чтобы заглянуть во внешнее пространство за пределами известной Вселенной. Но Икар подумал: «Я знаю столь же мало о том, что происходит на чрезвычайно малых расстояния х» и решил вместо больших исследовать крошечные размеры.
Однако Икар принадлежал к числу нетерпеливых людей. Он не мог заставить себя прочитать подробную инструкцию, прилагавшуюся к приобретенному им устройству, и вместо этого решил сразу двинуться вперед. Беспечно, не обращая внимания на красный индикатор, перекрывающий самые малые размеры, он набрал на дисплее расстояние 10-33 см и решительно нажал кнопку «вперед».
К своему ужасу, он обнаружил, что находится в дико колеблющейся обрывистой местности, заполненной струнами, и испытывает при этом сильнейшую тошноту. Пространство более не являлось гладким безликим фоном, к которому он привык. Напротив, оно быстро-быстро тряслось в одних местах, венчалось заостренными вершинками в других, или превращалось в петли, которые отсоединялись от поверхностей и затем воссоединялись с ними. Икар отчаянно стал искать кнопку «Стоп» и вовремя нажал на нее, чтобы вернуться к нормальному состоянию целым и невредимым.
Восстановив равновесие, Икар решил, что, вероятно, ему все же стоит прочитать руководство. Он раскрыл раздел «Предупреждение!» и прочел: «Ваша новая машина Алисэксвир, модель 6.3 работает только до расстояний, не меньших чем 10-33 см. Мы еще не включили новейшие достижения теории струн, предсказания которых физики и математики связали с физическим миром только в прошлом году».
Икар был сильно разочарован, когда понял, что только новейшая модель 7.0 включает последние результаты. Но затем он быстро подучил самые последние результаты теории струн, запустил на полную мощность свой Алисэксвир, и никогда больше не испытывал тошноты.
Общая теория относительности Эйнштейна была монументальной. С ее помощью физики намного глубже поняли гравитационное поле и сумели с беспрецедентной точностью рассчитать влияние гравитации. Теория относительности дала физикам в руки инструменты для предсказания эволюции всех гравитационных систем, даже всей Вселенной. Однако, несмотря на все эти успешные предсказания, общая теория относительности не может быть последним словом в гравитации. Общая теория относительности рушится, когда ее пытаются применять на очень малых расстояниях. На очень малых масштабах длины нужна новая гравитационная парадигма. Многие физики полагают, что такой парадигмой должна быть теория струн.
Если теория струн верна, она объединяет успешные предсказания общей теории относительности, квантовой механики и физики частиц. Но она также позволяет применить физику к таким расстояниям и энергиям, с которыми не приспособлены иметь дело другие теории. Теория струн все еще недостаточно развита для того, чтобы мы могли оценить ее предсказания при высоких энергиях и подтвердить эффективность этой теории в труднодоступных областях расстояний и энергий. Но теория струн все же имеет ряд примечательных свойств, которые вызывают доверие к этой многообещающей картине.
Бросим взгляд на теорию струн и эволюцию этой удивительной теории, кульминацией которой была «суперструнная революция» 1984 года, когда физики показали, что отдельные куски теории струн замечательно стыкуются друг с другом. Суперструнная революция была только началом интенсивной исследовательской программы, в которой принимают активное участие многие современные физики. В этой и следующей главах мы рассмотрим историю теории струн и ряд удивительных современных достижений этой теории. Мы увидим, что теория струн достигла заметных успехов и имеет многообещающие перспективы. Но мы увидим также, что теория струн сталкивается со многими сложнейшими проблемами, которые предстоит решить физикам, прежде чем использовать эту теорию для того, чтобы делать предсказания о нашем мире.
Зарождающееся беспокойство
Квантовая механика и общая теория относительности мирно сосуществуют в широком интервале расстояний, включая те, которые доступны экспериментальному анализу. Хотя обе теории должны быть применимы на всех масштабах длин, между ними существует взаимопонимание, какая из теорий должна доминировать на измеримых больших и малых расстояниях. Квантовая механика и общая теория относительности могут мирно разделить территорию, так как каждая теория признает главенство другой в обозначенной области. Общая теория относительности важна для массивных протяженных тел, таких как звезды или галактики. Но влияние гравитации на атом пренебрежимо мало, так что можно спокойно изучать атом, игнорируя общую теорию относительности. С другой стороны, квантовая механика критически важна на атомных расстояниях, так как ее предсказания для атома существенны и заметно отличаются от предсказаний классической физики.
Однако квантовая механика и теория относительности не находятся в полной гармонии. Эти две очень разные теории никогда не могли успешно преодолеть чрезвычайно малое расстояние, известное как планковский масштаб длины 10-33 см. Из ньютоновского закона тяготения мы знаем, что интенсивность тяготения пропорциональна массам и обратно пропорциональна квадрату расстояния между ними. Даже несмотря на то, что на атомных масштабах сила тяготения мала, закон тяготения утверждает, что на еще меньших масштабах сила тяготения огромна. Гравитация важна не только для очень массивных протяженных тел, но и для тел, которые находятся чрезвычайно близко друг к другу, разделенные крохотным планковским расстоянием. Если мы пытаемся сделать предсказания об этом неизмеримо малом расстоянии, и квантовая механика, и общая теория относительности дадут существенный вклад, причем вклады двух теорий будут несовместимы. На этой спорной территории, где расчеты с помощью квантовой механики и общей теории относительности расходятся и предсказания терпят неудачу, нельзя пренебречь ни квантовой механикой, ни тяготением.
Общая теория относительности работает только тогда, когда имеются плавно меняющиеся гравитационные поля, закодированные в постепенно искривляющемся пространстве-времени. Но квантовая механика утверждает, что все, что может прощупывать или влиять на планковский масштаб длины, имеет колоссальную неопределенность импульса. Пробное тело с энергией, достаточной для исследования планковского масштаба длины, будет порождать разрушительные динамические процессы, например, энергетические выбросы виртуальных частиц, которые разрушат всякую надежду на описание явления с помощью общей теории относительности. Согласно квантовой механике, на планковском масштабе длины вместо гладкой и волнообразно меняющейся геометрии будут происходить дикие флуктуации с ветвящимися ручками и петлями пространства-времени, порождая тот тип топографии, с которым через миллион лет столкнулся Икар. В такой дикой местности нельзя использовать общую теорию относительности.
Но общая теория относительности не может просто отойти в сторону, предоставив квантовой механике полную свободу действий, так как на планковском масштабе длины тяготение представляет собой существенную силу. Хотя тяготение ничтожно при тех энергиях физики частиц, к которым мы привыкли, оно очень сильно при высоких энергиях, которые требуются для изучения планковского масштаба длины[130]. Планковский масштаб энергии, т. е. та энергия, которая нужна для изучения планковского масштаба длины, как раз является той энергией, при которой тяготение уже не может рассматриваться как ничтожная сила. На планковском масштабе длины тяготением пренебрегать нельзя.
В действительности, на планковском масштабе энергии тяготение возводит барьеры, делающие обычные квантово-механические вычисления невозможными. Любое тело, обладающее достаточной энергией, чтобы исследовать расстояние в 10-33 см, будет захвачено черной дырой, которая берет в плен все, что только в нее попадает. Только квантовая теория гравитации может объяснить нам, что на самом деле происходит внутри.
На крохотных расстояниях квантовая механика и гравитация вопиют о более фундаментальной теории. Учитывая конфликт между ними, не остается иного выбора, кроме как пригласить внешнего арбитра в качестве альтернативы обоим теориям. Новый режим должен разрешать квантовой механике и общей теории относительности свободно править в своих бесспорных областях, но обладать равными правами управлять спорной областью, которую ни одна из старых теорий не контролирует. Возможным решением может быть теория струн.
Несовместимость квантовой механики и гравитации проявляется в бессмысленных предсказаниях, которые дает общепринятая теория тяготения для взаимодействий при высокой энергии частицы по имени гравитон, т. е. частицы, переносящей гравитационную силу в квантовой теории гравитации.
Согласно классической теории гравитации тяготение между массивными телами переносится гравитационным полем, во многом аналогично тому, как в классической электромагнитной теории Максвелла электромагнитное взаимодействие переносится от одной заряженной частицы к другой электромагнитным полем. Но квантовая электродинамика (КЭД), квантовая теория электромагнетизма, реинтерпретирует это классическое электромагнитное взаимодействие на языке обмена частицей — фотоном[131]. КЭД, теория фотонов, есть расширение классической теории электромагнетизма, включающее квантово-механические эффекты.
Квантовая механика требует, что по аналогии должна существовать частица, переносящая гравитационное взаимодействие. Эта частица и есть гравитон. В квантовой теории гравитации обмен гравитоном между двумя телами воспроизводит ньютоновский закон всемирного тяготения. Хотя гравитоны до сих пор непосредственно не наблюдались, физики уверены, что они существуют, так как квантовая механика говорит нам, что они есть.
Ниже для нас будет важен особый спин гравитона. Так как гравитоны переносят гравитацию — взаимодействие, тесно связанное с пространством и временем, то их спин отличается от спинов всех других известных переносчиков взаимодействий типа фотона. Мы не будем углубляться в причины этого, но гравитон — единственная безмассовая частица, спин которой равен 2, а не 1, как у других калибровочных бозонов, или 1/2, как у кварков и лептонов. Тот факт, что спин гравитона равен 2, окажется важным, когда мы перейдем к поиску убедительных свидетельств теорий с дополнительными измерениями. Кроме того, как мы вскоре убедимся, спин гравитона есть также ключ к пониманию потенциальных приложений теории струн.
Однако описание тяготения на языке квантовой теории поля не может быть полным. Ни одна квантовая теория поля для гравитона не может предсказать его взаимодействия при всех энергиях. Когда гравитон имеет энергию порядка планковского масштаба энергий, квантовая теория поля перестает работать. Теоретические соображения показывают, что дополнительные взаимодействия гравитона, не имеющие значения при низких энергиях, становятся важными при высоких энергиях, но логики квантовой теории поля оказывается недостаточно, чтобы сказать, что это за взаимодействия или как их включить в теорию. Если мы будем неправомерно использовать квантово-полевую теорию гравитации, игнорируя взаимодействия, не имеющие значения при низких энергиях, и попытаемся сделать предсказания для процессов с участием чрезвычайно энергичных гравитонов, мы придем к выводу, что взаимодействия гравитонов происходят с вероятностью больше единицы, что, очевидно, совершенно невозможно. На планковском масштабе энергий или эквивалентно (согласно квантовой механике и специальной теории относительности) на планковском масштабе длины 10-33 см, квантово-механическое описание гравитона, безусловно, разрушается.
Планковский масштаб длины, на девятнадцать порядков меньший размера протона, так мал, что вряд ли бы он заботил физиков, не будь с ним связана фундаментальная проблема, которая должна исследоваться в более полной теории. Например, современные космологические теории предполагают, что Вселенная началась как крохотный шар размером с планковский масштаб длины. Но мы совершенно не понимаем слова «взрыв» в Большом взрыве. Мы понимаем многое из последующей эволюции Вселенной, но не то, как она началась. Установление физических законов, применимых к размерам меньше планковского масштаба длины, должно пролить свет на сверхранние стадии эволюции нашей Вселенной.
Кроме того, существует много загадок, касающихся черных дыр. Важный нерешенный вопрос состоит в том, что точно происходит на горизонте черной дыры, т. е. месте невозврата, за которым ничто не может спастись от падения к центру, и в сингулярности — том месте в центре черной дыры, где уже не применима общая теория относительности. Другой не имеющий ответа вопрос — как сохраняется информация о телах, падающих в черную дыру. В отличие от испытываемого нами гравитационного взаимодействия, гравитационные эффекты внутри черной дыры сильны, так же как сильны эффекты взаимодействия тел с энергией порядка планковского масштаба энергий в обычном плоском пространстве. Мы никогда не решим эти загадки черных дыр, пока не разрешим проблему нахождения единственной теории, согласованно включающей квантовую механику и общую теорию относительности, — квантовой гравитации на планковском масштабе длины 10-33 см. Черные дыры дают примеры вопросов о сильных гравитационных явлениях, которые могут быть разрешены только с помощью квантовой теории гравитации. Наилучшим известным кандидатом на роль такой теории является теория струн.
Струнная разминка
Взгляд теории струн на фундаментальную природу материи существенно отличается от взгляда традиционной физики частиц. Согласно теории струн, самыми фундаментальными неделимыми объектами, лежащими в основе всей материи, являются струны — колеблющиеся одномерные петли или кусочки энергии. В противоположность, например, скрипичным струнам, эти струны не состоят из атомов, которые, в свою очередь, состоят из электронов и нуклонов, а те, в свою очередь, состоят из кварков. На самом деле верна в точности обратная картина. Струны фундаментальны, и это означает, что все, включая электроны и кварки, состоит из их колебаний. Согласно теории струн, моток пряжи, с которым играет кот, сделан из атомов, которые в конечном итоге составлены из колебаний струн.
Радикальная гипотеза теории струн состоит в том, что частицы возникают из резонансных мод колебаний струн. Каждая частица любого типа соответствует колебаниям лежащей в основе струны, а характер этих колебаний определяет свойства частицы. Так как существует много способов колебаний струн, отдельная струна может породить много типов частиц. Первоначально теоретики думали, что существует только единственный тип фундаментальной струны, ответственный за все известные частицы. Но в последние несколько лет эта картина поменялась, и теперь мы полагаем, что теория струн может содержать различные независимые типы струн, каждая из которых может колебаться множеством возможных способов.
Струны вытянуты в одном измерении. В каждый момент времени вам нужно лишь одно число, чтобы идентифицировать точку вдоль струны, так что, в соответствии с нашим определением размерности, струны являются пространственно одномерными объектами. Тем не менее, как реальные физические куски струны, они могут завиваться и образовывать петли. В действительности, существуют два типа струн: открытые струны, имеющие две концевых точки, и замкнутые струны, представляющие петли без концов (рис. 67).

То, какую частицу реально порождает струна, зависит от энергии струны и от точных колебательных мод, которые возбуждены. Моды струны похожи на резонансные моды скрипичной струны. Вы можете рассматривать колебания как элементарные единицы, которые можно комбинировать, образуя все известные частицы. На этом языке частицы — это аккорды, а их взаимодействия — это гармонии. Струна в теории струн не всегда порождает все частицы, так же как скрипичная струна не издает никакого звука, пока по ней не проведут смычком. Но так же как смычок возбуждает моды скрипки, энергия возбуждает моды струны. И если струна обладает достаточной энергией, она произведет разные типы частиц.
Как для открытой, так и для замкнутой струн резонансные моды — это те, колебания которых укладываются целое число раз вдоль длины струны. Несколько таких мод показано на рис. 68. Для этих мод волны колеблются вверх и вниз некоторое число раз и при этом все колебания полностью завершаются на длине струны. Для открытой струны волны ударяются о конец струны и поворачивают в противоположную сторону, продолжая бегать вперед и назад, а волны на замкнутых струнах колеблются вверх и вниз при распространении вдоль замкнутой петли. Любые другие волны, для которых на длине струны не умещается целое число колебаний, не возникают.
В конце концов, точный способ, которым колеблется струна, определяет все свойства частицы, такие как ее масса, спин и заряд. В общем случае будет существовать много копий частиц с тем же спином и зарядом, но с разными массами. Так как число таких мод бесконечно, отдельная струна может породить бесконечное число тяжелых частиц. Известные частицы, которые сравнительно легки, возникают от струн, совершающих самые слабые колебания. Модой без колебаний может быть знакомая легкая частица, например обычный кварк или лептон. Но струна большой энергии может колебаться многими способами, поэтому теория струн различается по самым тяжелым частицам, которые возникают от наивысших колебательных мод.

Однако большее количество колебаний требует больше энергии. Дополнительные частицы в теории струн, возникающие от большего числа колебаний, похоже, должны быть чрезвычайно тяжелыми — чтобы их породить, необходимо колоссальное количество энергии. Таким образом, даже если теория струн верна, ее новые следствия, похоже, будет очень трудно детектировать. Так как мы не ожидаем рождения любой из новых тяжелых частиц при доступных энергиях, мы полагаем, что теория струн и физика частиц приведут к одним и тем же наблюдаемым следствиям при тех энергиях, которые нам доступны. Такая картина может измениться, если окажутся верными некоторые из недавних достижений, касающиеся дополнительных измерений. Однако сейчас познакомимся с общепринятой картиной теории струн. Позднее мы займемся моделями с дополнительными измерениями.
Истоки теории струн
Ко времени Икара ХLII теория струн могла бы похвастаться довольно долгой историей. Но по научным соображениям мы ограничим нашу историю двадцатым и самым началом двадцать первого века. Мы сейчас рассматриваем теорию струн как теорию, которая могла бы объединить квантовую механику и гравитацию. Однако первоначально она имела совершенно иное приложение. Впервые теория возникла в 1968 году как попытка описать сильно взаимодействующие частицы, известные как адроны. Теория не была успешной; как мы видели в гл. 7, мы знаем теперь, что адроны состоят из кварков, удерживаемых вместе сильным взаимодействием. Тем не менее теория струн выжила, уже не как теория адронов, а как теория гравитации.
Несмотря на провал теории струн в описании адронов, мы можем кое-что узнать о хороших свойствах струнной теории гравитации, изучив несколько проблем, с которым столкнулась теория адронных струн. Примечательно, что провалы теории адронных струн оказались сильными сторонами (или, по крайней мере, не стали помехами) для струнной теории квантовой гравитации.
Первая проблема изначальной версии теории струн была в том, что теория содержала тахион. Поначалу ученые думали о тахионах как о частицах, движущихся со скоростью больше скорости света (термин произошел от греческого слова ταχύς, т. е. скорость). Но теперь мы знаем, что тахионы указывают на нестабильность в теории, которая их содержит. К сожалению для любителей научной фантастики, тахионы не являются реальными физическими частицами, существующими в природе. Если окажется, что ваша теория содержит тахион, вы неправильно ее проанализировали. Система, содержащая тахион, может (и должна) превратиться в родственную систему с меньшей энергией, в которой тахион отсутствует. Система, содержащая тахион, существует недостаточное время для того, чтобы возникли какие-то физические явления; это есть всего лишь свойство неправильного теоретического описания. Вам следует найти теоретическое описание родственной стабильной конфигурации без тахиона, прежде чем вы сможете идентифицировать истинные физические частицы и взаимодействия. До тех пор пока система содержит такую конфигурацию, ваша теория неполна.
Теория струн с тахионом казалась не имеющей смысла. Но никто не знал, как сформулировать теорию, чтобы исключить его. Это означало, что предсказания теории струн, в том числе для частиц, отличных от тахиона, были недостоверны. Вы можете подумать, что это дает достаточные основания отвергнуть адронную теорию струн. Но физики продолжали надеяться, что тахион не был реальным; некоторые думали, что это была проблема математических приближений, которые делались при формулировке теории, но это было маловероятно.
Однако Рамон, Невье и Шварц открыли альтернативную суперсимметричную версию струны — суперструну. Критически важное преимущество теории суперструн перед первоначальной версией теории струн состояло в том, что она содержала частицы спина 1/2, что дает потенциальную возможность описания фермионов Стандартной модели, таких как электрон и разные типы кварков. Но дополнительным бонусом теории суперструн было то, что она не содержала тахионы, которые так отравляли первоначальную версию теории струн. Теория суперструн, выглядевшая в любом случае более обещающей, не содержала тахионной нестабильности, которая могла бы помешать прогрессу теории.
Вторая проблема исходной теории адронных струн заключалась в том, что она содержала безмассовую частицу спина 2. Расчеты показали, что исключить эту частицу невозможно, но ни один экспериментатор никогда не наблюдал такую вредную частицу. Поскольку экспериментаторы должны были наблюдать любую безмассовую частицу, взаимодействующую так же сильно, как адрон, казалось, что адронная теория струн столкнулась с неприятностями.
Шерк и Шварц повернули теорию струн с ног на голову, показав, что «плохая» частица спина 2, мешающая адронной теории струн, могла на самом стать венцом струнной теории гравитации; частица спина 2 могла на самом деле быть гравитоном. Они доказали, что частица со спином 2 ведет себя так, как должен себя вести гравитон. Решающее наблюдение, что теория струн содержит кандидата на роль гравитона, сделало теорию струн потенциальной квантовой теорией гравитации. При описании на языке частиц никто не мог понять, как сформулировать согласованную теорию гравитации, которая работала бы при всех энергиях. В то же время описание на языке теории струн выглядело так, что этот фокус казался возможным.
Было и другое указание на то, что хотя теория адронных струн не работала, Шерк и Шварц могли быть на правильном пути к гравитационной теории струн. Как мы видели в гл. 7, Фридман, Кендалл и Тейлор из Станфордского ускорительного центра (SLAC) показали, что электроны удивительным образом рассеиваются на нуклонах, неявным образом демонстрируя существование внутри нуклонов твердых точечноподобных объектов, а именно, кварков. По духу этот эксперимент был аналогичен описанному в гл. 6 эксперименту Резерфорда по рассеянию. Поразительные результаты опыта по рассеянию в том случае указывали на существование твердого атомного ядра, а в этом случае — на существование внутри нуклона точечноподобных кварков, а не ворсистых протяженных струн.
Итак, предсказания теории струн не согласовывались с результатами эксперимента в SLAC. Струны никогда не могли бы привести к сильному рассеянию, причиной которого мог быть только жесткий компактный объект. Так как в любой данный момент времени взаимодействуют только кусочки струн, струны в целом сталкиваются более мягко. Такое спокойное, сравнительно слабое рассеяние было похоронным звоном для теории адронных струн. Но с точки зрения квантовой гравитации это выглядело многообещающим свойством.
В рамках корпускулярной теории гравитона эта частица взаимодействует при высоких энергиях слишком сильно. Более подходящей была бы теория, в рамках которой энергичные гравитоны не взаимодействовали бы столь яростно. Именно это и имело место в струнной теории гравитации. Теория струн, заменяющая точечноподобные частицы на протяженные струны, гарантирует, что гравитон взаимодействует при высоких энергиях существенно менее сильно. У струн, в противоположность кваркам, нет жестких процессов рассеяния. Их взаимодействия более «кашеподобные» и происходят в более протяженной области. Такое свойство означает, что теория струн может потенциально решить проблему удивительно сильной вероятности взаимодействия гравитона и правильно предсказать взаимодействия гравитона при больших энергиях. Более мягкие соударения струн при больших энергиях могли быть важным указанием на то, что струнная теория гравитации может оказаться правильной.
Подводя итог, можно сказать, что теория суперструн содержит фермионы, переносящие взаимодействия калибровочные бозоны и гравитон — все типы частиц, которые нам известны. Эта теория не содержит тахиона. Кроме того, теория суперструн включает гравитон, квантовое описание которого потенциально осмыслено при высоких энергиях. Теория струн выглядела так, как будто она потенциально могла описать все известные взаимодействия. Это был многообещающий кандидат на роль теории мира.
Суперструнная революция
Теория суперструн была очень смелым шагом даже в решении такой глубокой проблемы, как квантовая гравитация. Струнная теория гравитации предсказывает бесконечно большое число частиц помимо тех, которые нам известны. Кроме того, теорию струн чрезвычайно трудно анализировать с помощью вычислений. Не слишком ли высока цена за решение проблемы квантовой гравитации — теория с бесконечным числом новых частиц и потенциально неподатливым математическим описанием? В 1970-е годы разработка теории струн требовала участия личностей, которые были либо очень решительными и непоколебимыми, либо немного сумасшедшими. Шерк и Шварц были среди тех немногих, кто продолжал идти по этому рискованному пути.
После безвременной кончины Шерка в 1980 году Шварц упорно продолжал работу над теорией струн. Он сотрудничал с другим (возможно, единственным) верящим в эту идею, британским физиком Майклом Грином, и вместе они анализировали следствия теории суперструн. Шварц и Грин обнаружили удивительное свойство суперструны: она имеет смысл только в десяти измерениях, из которых девять пространственных и одно временное. При всех других числах измерений возникают неприемлемые колебательные моды струны, приводящие к явно бессмысленным предсказаниям, таким как отрицательные вероятности процессов, включающих моды струны, которые не должны существовать. В десяти измерениях все нежелательные моды взаимно устраняются. При любом другом числе измерений теория струн теряет смысл.
Чтобы сказанное стало яснее, заметим, что струна сама по себе вытянута вдоль единственного пространственного измерения и путешествует во времени. Это те два измерения, которые изучал Рамон, когда он впервые открыл суперсимметрию. Но точно так же, как мы знаем, что точечноподобный объект, не имеющий протяжения ни в одном пространственном измерении и, следовательно, имеющий нулевое число пространственных измерений, может перемещаться в трех пространственных измерениях, струна, имеющая одно пространственное измерение, может перемещаться в пространстве с много большим числом измерений, чем сама обладает. Струны могут, вероятно, перемещаться в трех, четырех и более измерениях. Вычисления показали, что правильное число измерений (включая время) равно десяти.
Слишком большое число измерений не было новым свойством суперструны. Более ранняя версия теории струн (не содержавшая фермионов или суперсимметрии) имела двадцать шесть измерений — одно временное и двадцать пять пространственных. Но в ранней версии теории струн были другие проблемы, например тахион. С другой стороны, теория суперструн была достаточно обещающей, чтобы над ней поработать.
Несмотря на все это, теорией струн практически пренебрегали до 1984 года, когда Грин и Шварц продемонстрировали поразительное свойство суперструны, которое убедило многих других физиков, что они идут по правильной дороге. Благодаря этому открытию, а также двум другим достижениям, которые мы вскоре рассмотрим, теория струн заняла основное место в потоке исследований по физике.
Работа Грина и Шварца была посвящена явлению, известному как аномалии. Как следует из названия, когда аномалии были впервые открыты, они стали большим сюрпризом. Первые физики, работавшие над квантовой теорией поля, принимали как данное то, что любая симметрия классической теории будет также сохраняться ее квантово-механическим расширением, т. е. более полной версией теории, включающей также эффекты виртуальных частиц. Но оказалось, что это не всегда так. В 1969 году Стивен Адлер, Джон Белл и Роман Джекив показали, что даже когда классическая теория сохраняет симметрию, квантовомеханические процессы с участием виртуальных частиц иногда эту симметрию нарушают. Такие нарушения симметрии называются аномалиями, а теории, содержащие аномалии, называются аномальными.
Аномалии очень важны для теории взаимодействий. В гл. 9 мы видели, что успешная теория взаимодействий требует существования внутренней симметрии. Эта симметрия должна быть точной, в противном случае невозможно исключить нежелательные поляризации калибровочного бозона, и теория взаимодействий не будет иметь смысла. Поэтому симметрия, связанная с взаимодействием, должна быть свободна от аномалий: сумма всех нарушающих симметрию эффектов должна равняться нулю.
Это мощное ограничение на любую квантовую теорию взаимодействий. Например, мы знаем сейчас, что это есть одно из самых убедительных объяснений существования в Стандартной модели и кварков, и лептонов. По отдельности виртуальные кварки и лептоны приводят к аномальным квантовым вкладам, которые нарушают симметрии Стандартной модели. Однако сумма квантовых вкладов от кварков и от лептонов равна нулю. Это чудодейственное сокращение и есть то, что скрепляет конструкцию Стандартной модели, — и кварки, и лептоны необходимы для того, чтобы взаимодействия в Стандартной модели обрели смысл.
Аномалии могли стать проблемой для теории струн, которая, помимо прочего, включает и взаимодействия. В 1983 году, когда теоретики Луис Альварес-Гауме и Эдвард Виттен показали, что такие аномалии возникают не только в квантовой теории поля, но и в теории струн, казалось, что это открытие отправит теорию струн в архив интересных в далекой перспективе, но пока неактуальных идей. Казалось, что теория струн не может сохранять требуемые симметрии. В атмосфере скептицизма, порожденного возможным существованием аномалий в теории струн, Грин и Шварц совершили сенсационное открытие, показав, что теория струн может удовлетворить ограничениям, которые нужны для того, чтобы избежать аномалий. Они вычислили квантовый вклад во все возможные аномалии и показали, что для определенных взаимодействий аномалии чудесным образом дают в сумме нуль.
Одна из причин, по которой результат Грина и Шварца был таким удивительным, состояла в том, что теория струн допускает много неприятных квантовомеханических процессов, каждый из которых мог бы породить нарушающие симметрию аномалии. Но Грин и Шварц показали, что сумма квантово-механических вкладов во все возможные нарушающие симметрию аномалии в десятимерной теории суперструн равна нулю. Это означало, что многие сокращения, требуемые в вычислениях теории струн, действительно происходят, более того, эти сокращения происходят в десяти измерениях, т. е. в том самом числе измерений, которое, как уже известно, является особым для теории суперструн. Сокращение аномалий было мощным аргументом в пользу десятимерной суперструны.
Кроме того, работа Грина и Шварца пришлась на очень удачное время. Физики безуспешно искали теории, которые могли бы расширить Стандартную модель, включив туда суперсимметрию и гравитацию, так что они были готовы рассмотреть что-то новое. Они не могли просто проигнорировать открытие Грином и Шварцем суперсимметричной теории, которая потенциально могла воспроизвести все частицы и взаимодействия Стандартной модели. И хотя дополнительная структура теории струн добавляла проблем, суперструна преуспела там, где другие более экономные теории потерпели крах.
Следующие два важных открытия закрепили за теорией струн место в анналах физики. Одно было сделано Принстонской группой — Дэвидом Гроссом, Джеффом Харви, Эмилем Мартинесом и Райаном Ромом, которые в 1985 году построили теорию, названую гетеротической струной. Это название происходит от греческого слова ϵτέρωσς, что в ботанике означает «сила гибрида», термин, используемый по отношению к гибридным организмам, обладающим свойствами, превосходящими свойства их предков. В теории струн колебательная мода может двигаться вдоль струны либо по часовой стрелке, либо против часовой стрелки. Название «гетеротический» использовалось потому, что волны, движущиеся налево, рассматривались не так, как волны, двигавшиеся направо, и, следовательно, теория включала более интересные взаимодействия, чем уже известные нам версии теории струн.
Открытие гетеротической струны было дальнейшим подтверждением того, что взаимодействия, которые, как обнаружили Грин и Шварц, были свободными от аномалий и допустимыми в десяти измерениях, были несомненно особыми. Они нашли несколько наборов взаимодействий, включая все те, которые, как уже было показано, возможны в теории струн, а также другие наборы взаимодействий, которые никогда ранее не считались (теоретически) частью теории струн. Взаимодействия гетеротической струны были теми самыми новыми взаимодействиями, для которых Грин и Шварц показали, что они свободны от аномалий. Было показано, что вместе с гетеротической струной это дополнительное множество взаимодействий, которое может включать взаимодействия Стандартной модели, является не только правильной возможностью теории струн, но и может быть явно реализовано. Физики рассматривали гетеротическую струну как реальный прорыв в попытке связать теорию струн со Стандартной моделью.
Наконец, было еще одно достижение, которое укрепило выдающееся положение теории струн. Это открытие имело дело с важными для теории струн дополнительными измерениями. Конечно, очень хорошо показать, что теория суперструн внутренне согласована и включает взаимодействия Стандартной модели, но все это мало интересно, если вы сталкиваетесь с неправильным числом измерений пространства. Теория суперструн накладывает обязательное условие в десять измерений. А в мире вокруг нас мы видим только четыре измерения (включая время). Что-то нужно делать с лишними шестью.
Сейчас физики считают, что одним из ответов может быть компактификация — скрученные измерения неощутимо малого размера, как описано в гл. 2. Однако вначале это сворачивание дополнительных измерений не представлялось правильной идеей для рассмотрения дополнительных измерений в теории струн. Проблема состояла в том, что теория со свернутыми измерениями не могла воспроизвести важное (и удивительное) свойство слабого взаимодействия, о котором шла речь в гл. 7: слабое взаимодействие рассматривает по-разному левые и правые частицы. Это не простая техническая деталь. Вся структура Стандартной модели основана на левых частицах, которые только и способны испытывать слабые взаимодействия. В противном случае будет выполняться лишь малая часть предсказаний Стандартной модели.
Хотя десятимерная теория струн может рассматривать по-разному левые и правые частицы, это перестает быть правильным, как только шесть дополнительных измерений сворачиваются. Результирующая эффективная четырехмерная теория всегда содержит закономерно смешанные пары левых и правых частиц. Все взаимодействия, которые действуют на левые формионы, действуют также на правые фермионы, и наоборот. Если теория струн не может найти выхода из этого тупика, ее следует пустить в отходы.
В 1985 году Филип Канделас, Гэри Горовиц, Энди Стромингер и Эдвард Виттен обратили внимание на более тонкий и сложный способ сворачивания дополнительных измерений, а именно, на компактификацию на многообразие Калаби — Яу. Детали сложны, но по существу многообразия Калаби — Яу сохраняют четырехмерную теорию, способную отличить левое от правого, и способны в принципе воспроизвести все частицы и взаимодействия Стандартной модели, включая нарушающее четность слабое взаимодействие. Кроме того, сворачивание дополнительных измерений в многообразие Калаби — Яу сохраняет суперсимметрию[132]. После прорыва, связанного с многообразиями Калаби — Яу, теория суперструн стала рабочей теорией.
На многих кафедрах физики теория суперструн вытеснила физику частиц, и суперсимметричная революция все больше напоминала переворот. Так как теория суперструн включает квантовую гравитацию и может содержать известные частицы и взаимодействия, многие физики зашли настолько далеко, что стали думать об этой теории как об окончательной теории, лежащей в основе всего. Действительно, в 1980-е годы теорию струн окрестили «Теорией Всего Сущего» (или ТВС). Теория струн была более амбициозна, чем даже ТВО: с помощью теории струн физики надеялись объединить все взаимодействия (включая гравитацию) при энергиях выше даже той энергии, которая ассоциируется с ТВО. Не имея ни одного экспериментального доказательства в пользу теории струн, многие физики решили, что способность теории струн к соединению квантовой механики и гравитации является достаточным основанием поддержать ее претензии на выдающееся положение.
Стойкость старого режима
Если теоретики — струнники правы и мир в конечном счете состоит из фундаментальных колеблющихся струн, то нужно ли прекратить занятия всей физикой частиц? Ответом является громкое «Нет». Целью теории струн является согласование квантовой механики и теории гравитации на расстояниях, меньших планковского масштаба длины, где, как мы полагаем, вступает в действие новая теория. Поэтому в рамках общепринятой теории струн (в противоположность вариантам, предлагаемым моделями с дополнительными измерениями) размер струны должен быть порядка планковского масштаба длины. Из этого следует, что в общепринятой теории струн различия между физикой частиц и теорией струн могут проявиться только на этих крохотных планковских масштабах длины или, эквивалентно, на ультравысоких планковских масштабах энергии, где считается, что гравитация становится сильной. Соответствующий размер настолько мал, а энергия настолько велика, что струны никак не смогут избежать описания на языке частиц при экспериментально доступных энергиях.
Для энергий ниже планковского масштаба энергий описание на языке физики частиц на самом деле вполне адекватно. Если струна настолько мала, что ее длина является недетектируемой, то она может с тем же успехом считаться частицей; ни один эксперимент не обнаружит разницы. Частицы и струны планковской длины неразличимы. Одномерная протяженность струны столь же невидима нами, как и крохотные свернутые дополнительные измерения, которые мы рассматривали выше. Пока у нас нет приборов, которые могли бы манипулировать с размерами порядка 10~33 см, такая струна слишком мала, чтобы мы ее увидели.
То, что теория струн и физика частиц выглядят одинаково при доступных энергиях, имеет глубокий смысл. Соотношение неопределенностей утверждает, что единственный способ изучения малых расстояний — использование частиц с большими импульсами, которые обладают очень большой энергией. Поэтому, если вы не обладаете достаточной энергией, у вас нет способа увидеть, что струна на самом деле длинная и тонкая, а не точечная.
В принципе можно искать свидетельства в поддержку теории струн, занимаясь поиском множества предсказываемых этой теорией частиц, соответствующих многим возможным осцилляциям струны. Трудность такой стратегии состоит в том, что большинство новых порожденных струной частиц должно быть очень тяжелыми, с массами порядка планковского масштаба масс 1019 ГэВ. Эта масса чудовищно велика по сравнению с массами экспериментально наблюдаемых частиц, самая тяжелая из которых имеет массу около 200 ГэВ.
Дополнительные частицы, которые должны возникать из колебаний струны, должны быть настолько тяжелыми по той причине, что натяжение струны, т. е. ее сопротивляемость растяжению, определяющая, насколько легко струна будет колебаться и порождать новые частицы, должно быть велико. Натяжение струны определяется планковским масштабом энергий. В теории струн это натяжение требуется для того, чтобы воспроизвести правильную интенсивность взаимодействия гравитона, а следовательно и самой гравитации. Чем больше натяжение струны, тем больше требуется энергии на то, чтобы порождать колебания (аналогично тому, как туго натянутую струну труднее дергать по сравнению со слабо натянутой). И эта большая энергия переводится в большую массу дополнительных частиц, порожденных струной. Такие частицы планковской массы слишком массивны, чтобы рождаться в каком-либо проводимом сегодня (и, вероятно, в будущем) эксперименте.
Итак, даже если теория струн правильна, нам вряд ли удастся найти множество дополнительных тяжелых частиц, которые она предсказывает. Энергия современных экспериментов на шестнадцать порядков величины меньше требуемой. Поскольку дополнительные частицы необычайно тяжелы, перспективы открытия экспериментальных свидетельств существования струн крайне слабы, если не считать возможного исключения — моделей с дополнительными измерениями, о которых мы поговорим ниже.
Из-за того, что длина струн столь мала, а натяжение так велико, в большинстве сценариев теории струн мы не найдем при доступных на ускорителях энергиях ни одного свидетельства в поддержку теории струн, даже если теория струн правильна. Физики-частичники, интересующиеся предсказанием экспериментальных результатов, вполне могут применять общепринятую четырехмерную квантовую теорию поля, игнорировать теорию струн и при этом все же получать правильные результаты. До тех пор пока вы изучаете только размеры, большие 10-33 см (или, эквивалентно, энергии ниже 1019 ГэВ), ничто из того, что мы рассматривали ранее относительно низкоэнергетических следствий физики частиц, не изменится. Полагая, что размер протона порядка 10-13 см, а максимальная энергия, достижимая на современных ускорителях, порядка тысячи ГэВ, можно спокойно делать ставку на то, что предсказаний физики частиц вполне достаточно.
Но даже если это так, у физиков-частичников, занимающиеся низкоэнергетическими явлениями, есть веские причины уделить внимание теории струн. Б этих теориях вводятся новые идеи, как математические, так и физические, которые никто ранее не рассматривал, например, браны и другие понятия, связанные с дополнительными измерениями. Даже в четырех измерениях теория струн проложила путь к углубленному пониманию суперсимметрии, квантовой теории поля и взаимодействий, которые могла бы содержать модель квантовой теории поля. И конечно, если теория струн действительно дает полностью согласованное квантово-механическое описание гравитации, это было бы потрясающим достижением. Все эти преимущества делают теорию струн весьма стоящей даже для тех, кто полностью сосредоточился на экспериментально доступных явлениях. Хотя обнаружить струны будет очень трудно (если вообще возможно), теоретические идеи, озаренные светом теории струн, могут иметь отношение к нашему миру. Вскоре мы увидим, как это может случиться.
Последствия революции
В 1984 году на пике «суперструнной революции» я была аспиранткой в Гарварде. Довольно скоро стало ясно, что в исследовательской работе у начинающего физика есть два пути. Он может признать теорию струн, следуя по стопам Эда Виттена и Дэвида Гросса, которые в то время работали в Принстоне. Или можно остаться физиком-частичником, имеющим более непосредственный контакт с экспериментальными результатами и работающим в команде под руководством Говарда Джорджи и Шелдона Глэшоу (оба в то время работали в Гарварде). Может показаться невероятным, что физики, интересовавшиеся одинаковыми проблемами, могли быть так разделены, но представления в двух лагерях о том, как достичь прогресса, были очень разными.
В Гарварде царило воодушевление по поводу физики частиц, и многие тамошние физики почти полностью отвергали теорию струн. В физике частиц и космологии оставались нерешенные вопросы — почему бы не ответить на них, прежде чем начать копаться на математическом минном поле, чем угрожала стать теория струн? Приемлемо ли для физики пытаться проникнуть в неизмеримые области? Когда имелось столько замечательных людей и множество интригующих идей о том, как расширить Стандартную модель физики частиц с помощью более традиционных методов, как-то не видно было особых причин бежать с корабля.
Однако были другие научные центры, где физики были убеждены, что все вопросы, касающиеся теории суперструн, будут вскоре разрешены, и что теория струн — это физика будущего (и настоящего). Теория суперструн находилась на ранних стадиях своего развития. Кое-кто верил, что если посвятить ей достаточное количество человеко-часов (а это были, в основном, муже-часы), теоретики-струнники смогут окончательно вывести всю известную физику. В работе 1985 года о гетеротической струне Гросс с коллегами писали: «Хотя остается еще много работы, представляется, что нет непреодолимых препятствий для того, чтобы вывести всю известную физику из… гетеротической струны»[133]. Теория струн обещала стать Теорией Всего Сущего. Принстон шел в авангарде этих идей.
Физики были настолько уверены, что теория струн была дорогой к будущему, что в отделе не осталось теоретиков в области физики частиц, не работавших над теорией струн, — ошибка, которую Принстону еще предстояло исправить.
Сегодня мы не можем сказать, являются ли проблемы, с которыми столкнулась теория, «непреодолимыми» или нет, но они, безусловно, требуют напряжения сил. На многие важные вопросы пока нет ответов. Обращение к нерешенным проблемам теории струн, по-видимому, требует математического аппарата или фундаментального нового подхода, которые далеко выходят за рамки того набора средств, который до сих пор был развит физиками и математиками.
Джо Полчинский в своем широко известном учебнике по теории струн пишет, что «теория струн может отражать набросок реального мира» и в некоторых отношениях это так и есть. Теория струн может включать частицы и взаимодействия Стандартной модели и может быть сведена к четырем измерениям, если свернуть остальные. Однако, хотя и существуют соблазн, что теория струн может включать в себя Стандартную модель, программа поиска идеального кандидата на роль такой модели после двадцатилетних усилий ничуть не приблизилась к завершению.
Первоначально физики надеялись, что теория струн сможет однозначно предсказать, на что должен был быть похож тот мир, из которого получился мир, который мы видим. Но сейчас в рамках теории струн существует множество моделей, которые содержат различные взаимодействия, имеют разные размерности и разные комбинации частиц. Мы хотим найти тот набор, который соответствует видимой Вселенной, и узнать причину, почему этот набор выделен. Пока что никто не знает, как сделать выбор среди возможностей. И в любом случае ни одна из них не выглядит безупречной.
Например, компактификация Калаби — Яу может объяснить число поколений элементарных частиц. Действительно, одна из возможностей — это три поколения Стандартной модели. Но компактификация Калаби — Яу не единственная. Хотя теоретики-струнники первоначально надеялись, что компактификация в многообразие Калаби — Яу выделит предпочтительную структуру и установит однозначные физические законы, они быстро разочаровались. Энди Стромингер рассказывал мне, что через неделю после открытия компактификации Калаби— Яу, когда он был уверен в ее однозначности, его соавтор Гэри Горовиц нашел еще несколько допустимых многообразий. Позднее Энди узнал от Яу, что существуют десятки тысяч допустимых многообразий Калаби — Яу. Сейчас мы знаем, что теории струн, основанные на компактификации Калаби — Яу, могут содержать сотни поколений. Если компактификации Калаби — Яу вообще имеют отношение к делу, то какая из них правильна? И почему? Даже если мы знаем, что некоторые измерения теории струн должны сворачиваться или как-то иначе исчезать, теоретики-струнники должны еще установить принципы, указывающие нам на размер и форму свернутых измерений.
Более того, кроме новых тяжелых струнных частиц, возникающих из волн, много раз колеблющихся вдоль струны, теория струн содержит новые частицы малой массы. Можно ожидать, что если они существуют и настолько легки, как это наивно предсказывает теория струн, такие частицы должны быть видны в экспериментах в нашем мире. Большинство основанных на теории струн моделей содержит намного больше легких частиц и взаимодействий, чем мы наблюдаем при низких энергиях, и совершенно не ясно, что выделяет правильные.
Найти теорию струн, соответствующую реальному миру, представляет собой чрезвычайно сложную задачу. Нам нужно еще узнать, почему гравитация, частицы и взаимодействия, выведенные из теории струн, должны совпадать с теми, которые существуют в нашем мире. Но эти проблемы с частицами, взаимодействиями и размерностями бледнеют по сравнению с реальным слоном в лавке — огромной переоценкой плотности энергии во Вселенной.
Даже в отсутствие частиц, Вселенная может обладать энергией, известной как энергия вакуума. Согласно общей теории относительности, существование такой энергии приводит к физическому следствию: она расширяет или сжимает пространство. Положительная вакуумная энергия ускоряет расширение Вселенной, в то время как отрицательная вакуумная энергия заставляет ее сжиматься. Эйнштейн впервые предположил существование такой энергии в 1917 году с целью найти статическое решение своих уравнений общей теории относительности, в котором гравитационный эффект энергии вакуума компенсировал бы влияние материи. Хотя затем он по многим причинам отверг эту идею, в том числе из-за открытого в 1929 году Эдвином Хабблом расширения Вселенной, не существует теоретической причины, по которой такая вакуумная энергия не могла бы существовать в нашей Вселенной.
Действительно, недавно астрономы измерили вакуумную энергию в нашем Космосе (ее еще называют темной энергией или космологической постоянной) и получили некоторое малое положительное значение. Они увидели, что далекие сверхновые тусклее, чем можно было бы ожидать, если бы они не разлетались ускоренно. Измерения сверхновых и детальные наблюдения реликтовых фотонов, рожденных во время Большого взрыва, убеждают нас, что Вселенная расширяется с ускорением, а это есть свидетельство того, что вакуумная энергия имеет малое положительное значение.
Это открытие очень важное. Но оно же порождает серьезную проблему. Ускорение очень мало, что говорит нам о том, что значение энергии вакуума хотя и ненулевое, но очень крохотное. Теоретическая проблема с наблюдаемой энергией вакуума состоит в том, что она намного меньше, чем кто-либо может оценить. Согласно оценкам теории струн эта энергия должна была бы быть намного больше. Но если бы это было так, энергия вакуума не просто приводила бы к трудноуловимому ускорению сверхновых. Если бы вакуумная энергия была большой, Вселенная уже давно бы сжалась (при отрицательной вакуумной энергии), или быстро расширилась в никуда (при положительной вакуумной энергии).
Теория струн должна еще объяснить, почему вакуумная энергия Вселенной столь мала. Физика частиц также не знает ответа на этот вопрос. Однако, в противоположность теории струн, физика частиц не претендует на то, чтобы быть теорией квантовой гравитации, она менее амбициозна. Модель физики частиц, которая неспособна объяснить энергию вакуума, неудовлетворительна, но теория струн, дающая неправильное значение этой энергии, вообще исключена.
Вопрос о том, почему плотность энергии столь экстраординарно мала, даже и близко не решен. Некоторые физики верят, что правильного объяснения не существует. Хотя теория струн есть единая теория с единственным параметром — натяжением растянутой струны — теоретики-струнники не могут до сих пор использовать ее для предсказания большинства свойств Вселенной. Большинство физических теорий содержит физические принципы, позволяющие вам отобрать те физические конфигурации, которые будет реально предсказывать теория. Например, большинство систем приходит в состояние покоя в конфигурации, имеющей наименьшую энергию. Но этот критерий, похоже, не работает для теории струн, в которой возможно бесконечное число различных конфигураций, не имеющих одинаковой вакуумной энергии, и мы не знаем, какую из них предпочесть.
Некоторые теоретики-струнники уже больше не пытаются найти однозначную теорию. Они смотрят на возможные размеры и формы скрученных измерений и на различные варианты значений энергии, которые может содержать Вселенная, и заключают, что теория струн может только набросать ландшафт, описывающий гигантское количество возможных вселенных, в которых мы могли бы жить. Эти теоретики не считают, что струна однозначно предсказывает вакуумную энергию. Они верят в то, что в космосе размещено много разных несвязанных областей с различными значениями вакуумной энергии, и мы живем в той части космоса, которая содержит правильное значение. Из множества возможных вселенных лишь одна может породить структуру, которая могла бы содержать (и действительно содержит) нас. Эти физики полагают, что мы живем во Вселенной с настолько фантастически невероятным значением вакуумной энергии, потому лишь что любое большее значение не привело бы к образованию галактик и структуры во Вселенной, а следовательно, предотвратило бы наше существование.
Это рассуждение известно под названием антропный принцип. Этот принцип существенно отличается от целей первоначальной теории струн — предсказать все свойства Вселенной. Он утверждает, что мы не должны объяснять малую энергию. Существуют несвязные вселенные со многими возможными значениями вакуумной энергии, но мы живем в одной из немногих, где может сформироваться структура. Значение энергии в этой вселенной до смешного мало, и только исключительные версии теории струн могут предсказать это очень маленькое значение, но мы можем существовать только во вселенной с очень малой энергией. Этот принцип может быть дискредитирован будущими достижениями, или оправдан более тщательными исследованиями. Однако, к сожалению, это будет трудно (если вообще возможно) проверить. Мир, в котором ответ зиждется на антропном принципе, определенно был бы неутешительным и неудовлетворительным сценарием.
В любом случае теория струн в ее теперешнем состоянии развития безусловно не предсказывает свойств мира, хотя это и единая теория по самой ее формулировке. Повторим снова, что мы столкнулись с вопросом о том, как связать прекрасную симметричную теорию с физическими реалиями нашей Вселенной. Простейшая формулировка теории слишком симметрична: многие размерности и многие частицы и взаимодействия, которые, как нам известно, должны быть разными, в теории совершенно одинаковы. И чтобы установить связь со Стандартной моделью и миром, который мы видим, этот великий порядок должен быть потревожен. После нарушения симметрии единственная теория струн может проявить себя во множестве разных обличий, в соответствии с тем, какие симметрии оказываются нарушенными, какие частицы становятся тяжелыми и какие измерения оказываются выделенными.
Создается впечатление, что теория струн — это красиво скроенное платье, которое не совсем подходит по размеру. В теперешнем состоянии вы можете повесить это платье на вешалку и восхищаться тонким шитьем и сложными стежками — оно действительно прекрасно — но вы не можете носить это платье, пока не сделаете необходимую подгонку. Нам нравится теория струн, которая включает все, что мы знаем о мире. Однако одежда, сшитая по правилу «один размер для всех», редко выглядит хорошо на каждом. Сейчас мы даже не знаем, есть ли у нас правильный набор инструментов, чтобы правильно сшить теорию струн.
Так как мы в действительности не знаем все приложения теории и неясно, будем ли мы их знать когда-нибудь, некоторые физики просто определяют теорию струн как все, что разрешает парадокс квантовой механики и общей теории относительности на малых расстояниях. Конечно, большинство теоретиков-струнников верят, что теория струн и правильная теория — это одно и то же или по крайней мере они очень тесно связаны.
Ясно, что многое еще нужно изучать. Еще слишком рано судить об окончательных достоинствах описания мира с помощью теории струн. Возможно, более искусная математическая машинерия позволит физикам по-настоящему понять теорию струн, или, возможно, физические идеи, запасенные в приложениях теории струн к окружающей Вселенной, подберут ключи к загадке. Для анализа нерешенных проблем теории струн, похоже, потребуется фундаментально новый подход, выходящий далеко за рамки тех средств, которые до сих пор развивали математики и физики.
Тем не менее теория струн очень примечательна. Она уже привела к углубленному пониманию гравитации, размерностей и квантовой теории поля и является наилучшим из всех нам известных кандидатов на роль последовательной теории квантовой гравитации. Кроме того, теория струн привела к невероятно красивым математическим достижениям. Но теоретики-струнники все еще не выполнили тех обещаний, которые были сделаны в 1980-е годы в отношении связи теории струн с миром. Мы до сих пор не знаем большинства следствий теории струн.
Честно говоря, вопросы физики частиц также не получили немедленного ответа. Многие проблемы физики частиц, известные в 1980-е годы, так и остались нерешенными. Среди этих вопросов объяснение происхождения несопоставимых по величине масс элементарных частиц и нахождение правильного решения проблемы иерархии. Кроме того, моделестроители все еще ждут экспериментальных ключей, которые подскажут нам, какая из мириад возможностей правильно описывает физику за рамками Стандартной модели. Пока мы не перейдем к энергиям выше 1 ТэВ, мы вряд ли получим определенные ответы на волнующие нас вопросы.
В наши дни как сообщество физиков, занимающееся теорией струн, так и сообщество специалистов по физике частиц имеют более здравый взгляд на свой уровень понимания, чем это было в 1980-е годы. Мы пытаемся задавать трудные вопросы, а они требуют времени на ответ. Но это волнующее время, так что несмотря на (или, возможно, из-за) множества нерешенных проблем, есть хорошие основания быть оптимистом. Сейчас физики более глубоко понимают многие следствия как физики частиц, так и теории струн, и те исследователи, которые непредвзято воспринимают новые идеи, получают выгоду от достижений обеих школ. Это «срединная» позиция, которую предпочитают некоторые мои коллеги и я сама, и она приводит к потрясающим результатам, с которыми мы скоро познакомимся.
Что стоит запомнить
• Гравитон — это частица, переносящая гравитационное взаимодействие, во многом аналогично тому, как фотон переносит электромагнитное взаимодействие.
• Согласно теории струн, фундаментальными объектами в мире являются струны, а не точечноподобные частицы.
• Современные модели дополнительных измерений не используют явно теорию струн. На расстояниях, превышающих крохотный планковский масштаб длины (10-33 см), достаточно физики частиц.
• Тем не менее теория струн важна для физики частиц даже при низких энергиях благодаря новым понятиям и аналитическим инструментам, которые она вводит.
Глава 15
Вспомогательные пассажи: развитие бран
Insane in the membrane
Insane in the brain.
Cypress Hill[134]
Икар Рашмор XLII решил еще раз нырнуть на крохотный планковский масштаб. К счастью, его Алисэксвир с форсированным движком работал превосходно и Икар плавно возник в десятимерной вселенной, заполненной струнами. Желая поскорее испытать свое новое оборудование, Икар запустил на полную мощность только что купленный по системе Gbay1 гипердвигатель. Он с восхищением наблюдал за тем, как струны сталкивались и перепутывались в чарующем танце.
Хотя Икар опасался, что Алисэксвир может не выдержать, ему очень хотелось побольше узнать об этом новом мире. Поэтому он продолжал давить на рычаг гипердвигателя. Сначала струны стали еще чаще сталкиваться друг с другом. Но когда Икар сильнее надавил на рычаг, он попал в новый, совершенно неузнаваемый мир. Икар даже не мог сказать, не разрушилось ли пространство-время. Но он продолжал разгонять гипердвигатель и, как ни странно, остался целым и невредимым.
Однако окружающий его мир стал совершенно иным. Икар уже не находился в десятимерной вселенной, откуда он начал свое путешествие. Вместо этого он оказался в одиннадцатимерной вселенной, заполненной частицами и бранами. И, как это ни странно звучит, ничто в этой новой вселенной не испытывало тяги к взаимодействию. Бросив взгляд на свои контрольные приборы, Икар обнаружил, что рычаг форсажа загадочным образом вернулся в нижнее положение. Озадаченный и довольно раздраженный Икар снова нажал на рычаг только для того, чтобы вернуться назад, откуда он начал. Проверив приборы, он обнаружил, что рычаг гипердвигателя опять находится в нижнем положении.
Икар подумал, что его Алисэксвир, вероятно, работает неправильно. Но когда он сверился с руководством, он понял, что устройство работает идеально, просто запущенный на полную мощность гипердвигатель в десятимерной теории струн был эквивалентен маломощному гипердвигателю в альтернативном одиннадцатимерном мире, и наоборот.
Руководство не говорило, что должно происходить, когда гипердвигатель работал на промежуточной мощности, не слишком малой и не слишком большой, так что Икар вошел в Спейсернет3 и занес себя в очередь ожидающих исправленной версии машины, которая решила бы проблему. Но создатели Алисэксвира обещали только, что выпуск нового релиза состоится в пределах тысячи лет.
Можно сказать, что в современном физическом мире термин «теория струн» стал неадекватным. Так, теоретик Майкл Дафф шутливо называет «теорию струн» «теорией, ранее известной как струны». Теория струн уже давно является не просто теорией струн, простирающихся в одном пространственном измерении, но также теорией бран, простирающихся в двух, трех и более измерениях. Сейчас мы знаем, что браны, которые могут простираться в любом числе измерений вплоть до того числа, которое содержит теория суперструн, являются в такой же степени частью теории суперструн, как и сами струны. Ранее теоретики игнорировали их, так как они изучали струны в условиях, когда «рычаг» интенсивности взаимодействия струн находился в нижнем положении, и взаимодействия бран были менее существенны. Оказалось, что браны есть тот пропавший кусок, который удивительным образом дополнил ряд картинок-загадок.
В этой главе я опишу эволюцию бран в истории теории струн. Они появились как забавная диковинка, которой можно пренебречь, и со временем превратились в центрального игрока. Мы увидим несколько направлений, следуя которым браны помогли разрешить ряд неясных с середины 1990-х годов вопросов теории струн. Браны помогли физикам понять происхождение загадочных частиц в теории струн, которые, как казалось, не могли возникнуть из струн. А когда физики включили в рассмотрение браны, они открыли дуальные теории — пары теорий, казавшихся весьма различными друг от друга, но имевших одинаковые физические следствия. История про Икара относится к одному поразительному примеру дуальности, который будет использован в этой главе: эквивалентность между десятимерной теорией суперструн и одиннадцатимерной супергравитацией, представляющей собой теорию, в которой есть браны, но нет струн.
В этой главе будет также представлена М-теория, одиннадцатимерная теория, охватывающая как теорию суперструн, так и одиннадцатимерную супергравитацию, существование которой было предсказано с помощью идей, пришедших от теории струн. Никто на самом деле не знает, что означает «М» в названии теории — изобретатель термина Эдвард Виттен умышленно оставил это неясным, но в числе предложений есть слова «мембрана» (membrane), «магия» (magic) и «тайна» (mystery). Здесь я хотела бы добавить, что М-теория все еще остается «отсутствующей теорией» (missing theory), которая постулирована, но не до конца понятна. Однако, даже несмотря на то, что многие вопросы в М-теории остаются без ответа, полученные с помощью бран новые результаты выявили теоретические связи, предполагающие у М-теории наличие более сложной структуры. Именно поэтому теоретики-струнники изучают ее сейчас.
В этой главе мы обновим картину теории струн, которая начала развиваться в 1980-е годы, и представим ряд новых точек зрения, развитых физиками в 1990-е годы. Значительная часть этого материала не будет важна для рассмотрения вопроса о применении бран к физике частиц, и дальнейшие гипотезы о мире бран не будут явно опираться ни на одно из описанных ниже явлений. Поэтому при желании вы можете пропустить эту главу. Однако воспользуйтесь этой возможностью и познакомьтесь с рядом удивительных достижений теории струн, которые и объясняют в значительной степени важность бран в этой теории.
Рождающиеся браны
В гл. 3 мы видели, что браны простираются в некоторых пространственных измерениях (необязательно во всех). Например, браны могут простираться только в трех пространственных измерениях, хотя число пространственных измерений балка намного больше. Дополнительные измерения могут оканчиваться на бранах, иначе говоря, браны могут ограничивать пространство дополнительных измерений. Мы знаем также, что брана может приютить частицы, движущиеся только в ее измерениях. Даже если бы существовало много дополнительных пространственных измерений, захваченные браной частицы двигались бы только в ограниченной области, занятой этой браной; они не могли бы использовать все пространство дополнительных измерений.
Сейчас мы увидим, что браны представляют собой нечто большее, чем просто место; они сами являются объектами. Браны похожи на мембраны, и так же, как мембраны, они вполне реальны. Браны могут быть ненатянутыми, и в этом случае они могут двигаться и изгибаться, или они могут быть натянутыми, и в этом случае скорее всего неподвижны. Браны могут обладать зарядами и разным образом взаимодействовать. Кроме того, браны влияют на то, как ведут себя струны и другие объекты. Все эти свойства позволяют утверждать, что браны существенны для теории струн — любая последовательная формулировка теории струн должна включать браны.
В 1989 году Джин Дай, Роб Ли и Джо Полчинский, в то время работавшие в Техасском университете, и независимо чешский физик Петр Хоржава математически доказали существование в уравнениях теории струн решений в виде определенного типа бран, названных D-бранами (в честь Петера Дирихле, немецкого математика XIX века). В отличие от замкнутых струн, которые образуют петлю, открытые струны имеют два свободных конца. Эти концы должны где-то находиться, и в теории струн разрешенные местонахождения концов открытой струны представляют собой D-браны. Балк может содержать более одной браны, так что не все струны обязательно заканчиваются на одной и той же бране. Но Полчинский, Дай, Ли и Хоржава обнаружили, что все открытые струны должны кончаться на бранах, а теория струн показывает, какую размерность и свойства будут иметь эти браны.
Одни браны простираются в трех измерениях, другие — в четырех, пяти и более измерениях. На самом деле теория струн содержит браны, простирающиеся в любом числе измерений вплоть до девяти. Соглашение, принятое в теории струн для нумерации бран, заключается в том, чтобы указывать число измерений пространства, но не пространства-времени, в котором они простираются. Например, 3-брана — это брана, простирающаяся в трех измерениях пространства (но четырех измерениях пространства-времени). Когда мы дойдем до следствий, которые браны оказывают на видимый мир, 3-браны окажутся очень важными. Однако для приложений, которые обсуждаются в этой главе, браны с другим числом измерений также будут играть важную роль.
В теории струн возникают разные типы бран. Они отличаются не только своей размерностью — числом измерений, в которых они простираются, но и своими зарядами, формой и важной характеристикой, называемой натяжением (к которой мы вскоре подойдем). Мы не знаем, существуют ли браны в реальном мире, но мы знаем все типы бран, возможные в теории струн.
Когда браны были открыты, они казались просто диковинкой. Никто не видел в то время хоть какой-нибудь причины включать в рассмотрение браны, которые бы взаимодействовали или двигались. Если бы струны взаимодействовали только слабо, как изначально предполагали теоретики-струнники, D — браны были бы столь сильно натянутыми, что они просто сидели бы неподвижно и не вносили никакого вклада в движение или взаимодействия струн. Если же браны не соответствовали струнам в балке, они были бы просто излишним усложнением. Они означали бы место или положение, но имели бы отношение к движениям и взаимодействиям струн не более, чем Великая Китайская стена имеет отношение к нашему повседневному существованию. Кроме того, физики не хотели включать браны в физическую реализацию теории струн, так как браны нарушали их интуитивное понимание того, что все размерности созданы равноправными. Браны различали некоторые измерения — те, которые простирались вдоль браны, от тех, которые простирались вне браны, в то время как в известных законах физики все направления считались одинаковыми. Почему же теория струн должна быть иной?
Мы также считаем, что физика в любой точке пространства должна быть такой же, как в любой другой точке. Но браны не соблюдают и эту симметрию. Хотя браны и простираются по некоторым измерениям бесконечно далеко, по другим измерениям их положение фиксировано. Именно поэтому они не покрывают все пространство. Но в тех направлениях, в которых положение бран фиксировано, сантиметр в сторону от браны — не то же самое, что метр или километр. Вообразите брану, надушенную духами. Вы, безусловно, сможете сказать, находитесь ли вы близко или далеко от нее.
По этим причинам физики первоначально игнорировали браны. Однако через пять лет после открытия бран их статус в среде теоретиков заметно исправился. В 1995 году Джо Полчинский необратимо изменил направление исследований в теории струн, показав, что браны — это динамические объекты, являющиеся неотъемлемой частью теории струн и способные играть решающую роль в ее окончательной формулировке. Полчинский объяснил, какие типы D-бран присутствуют в теории суперструн, и показал, что эти браны обладают зарядом и, следовательно, взаимодействуют.
Кроме того, браны в теории струн обладают конечным натяжением. Оно чрезвычайно похоже на натяжение поверхности барабана, которая возвращается после растяжения или сжатия к своему исходному натянутому положению. Если бы натяжение браны равнялось нулю, любое малое прикосновение приводило бы к огромному эффекту, так как у браны не было бы сопротивления. С другой стороны, если бы натяжение браны было бесконечно велико, вы, прежде всего, не могли бы никак на нее воздействовать, так как это был бы стационарный, а не динамический объект. Так как натяжение бран конечно, они могут двигаться, флуктуировать и реагировать на взаимодействия, как и всякий другой заряженный объект.
Конечное натяжение бран и их ненулевой заряд говорят нам о том, что они не просто задают положение, они являются также предметами: их заряды указывают нам, что они взаимодействуют, а конечное натяжение указывает на то, что они движутся. Брана может двигаться и взаимодействовать, как батут — поверхность, взаимодействующая с окружающей средой, когда ее сжимают, а затем она выпрямляется. Например, и батут, и браны могут быть изогнуты. И батут, и браны могут влиять на их окружение, батуты путем выталкивания людей и воздуха, а браны — путем толкания заряженных объектов и гравитационного поля.
Если браны существуют в космосе, нарушение ими пространственно-временных симметрий должно беспокоить нас не больше, чем нарушение пространственных симметрий, вызванное Солнцем и Землей. Солнце и Земля также находятся в определенных местах; при измерении относительно Солнца или Земли не все положения в трехмерном пространстве равноценны. Тем не менее физические законы сохраняют пространственно-временные симметрии трехмерного пространства, даже если это не справедливо для состояния вселенной. В этом отношении браны должны быть не хуже, чем Солнце или Земля. Как и все другие объекты, занимающие определенные положения в пространстве, браны нарушают некоторые симметрии пространства-времени.
Небольшое размышление показывает, что в этом нет ничего плохого. В конце концов, если теория струн является правильным описанием природы, тогда не все измерения созданы равными. Три знакомых пространственных измерения выглядят похоже, но дополнительные измерения должны быть другими; если бы это было не так, они не были бы «дополнительными». С точки зрения физической вселенной нарушение пространственно-временных симметрий могло бы помочь объяснить, почему дополнительные измерения различны: браны могли бы корректно отличать дополнительные измерения теории струн от трех пространственных измерений, которые мы знаем и ощущаем.
В последующих главах я буду рассматривать браны с тремя пространственными измерениями и опишу некоторые возможные радикальные следствия для реального мира. Но в данной главе мы сосредоточимся на том, почему браны оказались столь важными в теории струн, настолько важными, что они привели в 1995 году ко «второй суперструнной революции». В следующем разделе приводится ряд соображений, почему в прошедшее десятилетие браны оставались на переднем крае теории струн, и почему мы сейчас думаем, что они должны там оставаться.
Взрослые браны и пропавшие частицы
В то время, когда Джо Полчинский был поглощен исследованием D-бран, Энди Стромингер, в то время его коллега в университете Санта-Барбара, обдумывал р-браны, поразительные объекты, вытекающие из уравнения Эйнштейна. Они простираются бесконечно далеко в некоторых пространственных измерениях, но в оставшихся измерениях ведут себя как черные дыры, захватывая все объекты, которые подходят слишком близко. А вот D-браны — это поверхности, на которых заканчиваются открытые струны.
Энди рассказал мне, как каждый день за обедом он и Джо обсуждали свои исследования. Энди говорил о р-бранах, а Джо обсуждал D-браны. Хотя они оба исследовали браны, поначалу, как и все физики, они думали, что их браны являются разными вещами. В конце концов Джо понял, что это не так.
Работа Энди показала, что р-браны, которые он изучал, крайне важны для теории струн, так как в определенных пространственно-временных геометриях они порождают новые типы частиц. Даже если допустить, что столь неочевидные идеи теории струн верны и частицы возникают как колебательные моды струн, колебания струн совсем не обязаны объяснять существование всех частиц. Энди показал, что могут существовать дополнительные частицы, возникающие независимо от струн.
Браны могут иметь разные образы, формы и размеры. Хотя мы сфокусировались на них как на месте, где заканчиваются струны, сами браны являются независимыми объектами, которые могут взаимодействовать со своим окружением. Энди рассмотрел р-браны, которые обворачиваются вокруг очень маленькой скрученной области пространства, и обнаружил, что эти сильно скрученные браны могут действовать как частицы. Скрученную р-брану, действующую как частица, можно сравнить с сильно затянутым лассо. Веревочная петля становится маленькой, как только вы набросите лассо на шест или рог быка и стянете петлю, так и брана может затянуться вокруг компактной области пространства. И если эта область пространства мала, то и брана, охватывающая эту область, также будет малой.
Эти маленькие браны, как и более знакомые макроскопические объекты, обладают массой, линейно растущей в зависимости от размера. Большое количество чего-нибудь (например, свинцовых труб, грязи или вишен) тяжелее, а меньшее количество легче. Так как окружающая крохотную область пространства брана очень мала, она будет и чрезвычайно легкой. Расчеты Энди показали, что в предельном случае, когда брана настолько мала, как это только можно себе представить, такая крохотная брана выглядит как новая безмассовая частица. Результат Энди был очень важным, так как он показывал, что даже самая основная гипотеза теории струн — все состоит из струн — не всегда верна. Браны тоже вносят вклад в спектр частиц.
Важное наблюдение Джо в 1995 году состояло в том, что эти новые частицы, возникающие из крохотных р-бран, можно также объяснить с помощью — D-бран. Действительно, в работе, устанавливающей важность D-бран, Джо показал, что D-браны и р-браны — на самом деле одно и то же. При тех энергиях, когда теория струн и общая теория относительности дают одинаковые предсказания, D-браны превращаются в р-браны. Джо и Энди на самом деле изучали одни и те же объекты, хотя поначалу они этого не понимали. Полученный результат означал, что в важности — D-бран уже нельзя более сомневаться: они не менее важны, чем р-браны, а р-браны существенны для спектра частиц теории струн. Кроме того, появился красивый способ понять, почему р-браны эквивалентны. D-бранам. Он основан на тонком и важном понятии дуальности.
Зрелые браны и дуальность
Дуальность — ОДНО из самых интересных понятий последних десяти лет в физике частиц и теории струн. Она играет главную роль в недавних успехах как квантовой теории поля, так и теории струн, и, как мы вскоре увидим, имеет особенно важные приложения для теорий с бранами.
Две теории дуальны, если они являются одной и той же теорией, но при разных описаниях. В 1992 году индийский физик Ашок Сен одним из первых заметил дуальность в теории струн. В своей работе, развивавшей идею дуальности, которую первоначально предложили в 1977 году физики Клаус Монтонен и Дэвид Олив, он показал, что некая теория остается в точности такой же, что и раньше, если частицы и струны в теории меняются местами. В 1990-е годы родившийся в Израиле физик Нати Зейберг, работавший затем в Университете Ратгерса, также продемонстрировал удивительные дуальности между различными супер-симметричными теориями поля с кажущимися различными взаимодействиями.
Чтобы понять важность понятия дуальности, полезно иметь небольшое представление о том, каким образом теоретики-струнники в общем случае производят вычисления. Предсказания теории струн зависят от натяжения струны. Но они зависят также от величины, называемой константой связи струны, которая определяет интенсивность взаимодействия струн. Скользят ли они мимо, чуть касаясь друг друга, что соответствует малой константе связи, или прилипают друг к другу, обсуждая свою дальнейшую судьбу, что соответствует сильной константе? Если бы мы знали величину константы связи струны, мы могли бы изучать теорию струн только для этого конкретного значения. Но так как мы до сих пор не знаем значения константы связи струны, мы можем надеяться понять теорию только в случае, если сможем сделать предсказания для любого значения константы взаимодействия струн. Тогда мы сможем найти, какой из вариантов работает.
Проблема заключалась в том, что с первых шагов теории струн казалось, что теория с большой константой связи очень неподатлива. В 1980-е годы была понята только теория струн со слабо взаимодействующими струнами. (Я использую прилагательное «слабый» для описания интенсивности взаимодействий струн, но пусть это слово не введет вас в заблуждение — оно не имеет ничего общего со слабым взаимодействием.) Когда струны взаимодействуют очень сильно, невероятно трудно произвести хоть какие-нибудь вычисления. Точно так же, как проще развязать слабый узел, чем тугой, теория, в которую входят только слабые взаимодействия, значительно более податлива, чем теория с сильными взаимодействиями. Когда струны взаимодействуют друг с другом очень сильно, они превращаются в сильно запутанный клубок, который слишком трудно распутать. Физики испытывали различные хитроумные подходы для расчетов, включающих сильно взаимодействующие струны, но не нашли методов, которые можно было бы с пользой применить к реальному миру.
На самом деле не только теорию струн, но все физические теории легче понимать, когда взаимодействия слабы. Происходит это потому, что если слабое взаимодействие является всего лишь малым возмущением, или отклонением от решаемой теории (обычно теории без взаимодействия), то вы можете использовать технику, известную как теория возмущений. Эта теория позволяет постепенно накапливать ответ на вопрос о слабовзаимодействующей теории, начав с теории без взаимодействий и шаг за шагом вычисляя малые поправки. Теория возмущений — это систематическая процедура, говорящая нам, как улучшить расчет последовательными шагами, пока вы не достигнете любого желаемого уровня точности (или пока вы не устанете, что бы ни произошло раньше).
Использование теории возмущений для приближенного вычисления величины в нерешаемой теории можно сравнить со смешиванием красок для приближенного получения желаемого цвета. Допустим, вы стремитесь получить нежноголубой цвет с примесью зеленого, который напоминает Средиземное море в самые красивые моменты. Вы можете начать с синей краски, а затем подмешивать во все меньших количествах зеленую краску, поочередно добавляя чуть больше синей, пока не достигнете (почти) точного цвета, которого вы добивались. Изменение вашей смеси красок в такой манере — это путь, совершаемый малыми шагами для получения настолько близкого приближения к желаемому цвету, который вы хотите. Аналогично, теория возмущений — это метод последовательного приближения к правильному ответу для любой задачи, которую вы решаете, путем совершения последовательных шагов, начиная с задачи, которую вы уже знаете, как решать.
С другой стороны, попытка найти ответ для задачи в теории с сильной связью больше напоминает попытку воспроизвести картину Джексона Поллака, хаотично распыляя краски. Каждый раз, как вы брызгали бы немного краски, картина полностью менялась бы. Ваша картина не стала бы ближе к желаемой после двенадцати итераций по сравнению с тем, чем она была после восьми. На самом деле каждый раз, когда вы разбрызгивали бы краску, вы старались бы сделать это так, чтобы не покрыть слишком большой кусок от предыдущей попытки, изменяя картину настолько сильно, что вы по существу начинали бы каждый раз заново.
Аналогично, теория возмущений бесполезна, когда решаемая теория возмущается сильным взаимодействием. Так же как тщетны попытки повторить современный разбрызганный шедевр, не будут иметь успеха и систематические попытки получить приближенно интересующую вас величину в теории с сильным взаимодействием. Теория возмущений полезна и вычисления можно контролировать только тогда, когда взаимодействия слабы.
Иногда, в определенных исключительных ситуациях, даже когда теория возмущений бесполезна, удается все же понять качественные свойства сильно взаимодействующей теории. Например, физическое описание вашей системы может напоминать в общих чертах слабовзаимодействующую теорию, хотя детали, возможно, довольно сильно различаются. Однако чаще невозможно что-либо сказать о сильновзаимодействующей системе. Даже качественные свойства сильновзаимодействующей системы часто полностью отличаются от свойств на первый взгляд похожей слабовзаимодействующей системы.
Итак, есть две вещи, которые можно ожидать от сильновзаимодействующей десятимерной теории струн. Вы можете думать, что никто не способен построить ее, и поэтому никто не может ничего о ней сказать, или вы можете ожидать, что сильновзаимодействующая десятимерная теория струн выглядит, по меньшей мере в общих чертах, как слабо связанная теория струн. Удивительно, но в некоторых случаях ни один из этих вариантов не оказывается правильным. В случае частного типа десятимерной теории струн, называемой НА, сильновзаимодействующая струна не имеет ничего общего со слабовзаимодействующей струной. Но тем не менее мы можем изучать ее следствия, так как это податливая система, в которой возможны расчеты.
На конференции «Струны-95», которая проходила в Университете Южной Калифорнии в марте 1995 года, Эдвард Виттен поразил аудиторию, показав, что при низких энергиях вариант десятимерной теории суперструн с сильной связью полностью эквивалентен теории, которую большинство ученых считало совершенно иной, а именно, одиннадцатимерной супергравитации, т. е. одиннадцатимерной суперсимметричной теории, содержащей гравитацию. Объекты этой эквивалентной теории супергравитации взаимодействовали слабо, так что можно было с пользой применять теорию возмущений.
Как это ни странно, это означало, что можно использовать теорию возмущений для изучения исходной сильновзаимодействующей десятимерной теории суперструн. Вам нужно было использовать теорию возмущений не в самой сильно-взаимодействующей теории струн, а, на первый взгляд, в совершенно другой теории — слабовзаимодействующей одиннадцатимерной супергравитации. Этот важный результат, ранее замеченный также Полом Таунсендом из Кембриджского университета, означал, что несмотря на разную упаковку при низких энергиях десятимерная теория суперструн и одиннадцатимерная супергравитация были на самом деле одной и той же теорией. Как принято говорить у физиков, эти теории были дуальны.
Идею дуальности можно проиллюстрировать нашей аналогией с живописью. Предположим, что мы начали с синей краски, но затем «возмутили» ее, добавив зеленой краски. Хорошим описанием такой смеси красок будет тогда синяя краска с намеком на зеленую. Теперь предположим, что добавленная зеленая краска была не малым возмущением, а мы добавили огромное количество зеленой краски. Если это количество намного превосходит количество исходной синей краски, то более правильным, «дуальным» описанием смеси будет зеленая краска с намеком на синюю. Предпочтительное описание полностью зависит от количества каждой краски.
Аналогично, когда константа взаимодействия мала, теория может иметь одно описание. Но когда эта константа достаточно велика, теория возмущений в исходном описании становится бесполезной. Тем не менее в определенных важных ситуациях исходную теорию удается полностью переделать так, что теория возмущений становится применимой. Это и будет дуальным описанием.
Все это напоминает ситуацию, когда кто-то преподносит вам продукты для обеда из пяти блюд. Даже имея все составные части, вы можете не знать, с чего начать. Чтобы приготовить блюдо, вы должны представлять, для какого блюда предназначены определенные продукты, как специи взаимодействуют с пищей и друг с другом, что и когда нужно запекать. Но если поставщики провизии доставили те же составные части предварительно приготовленными и превращенными в салат, суп, закуску, главное блюдо и десерт, то я полагаю, что каждый сумеет превратить это в обед. Когда те же самые составные части правильно организованы, приготовление обеда превращается из сложной задачи в тривиальную.
Аналогично работает и дуальность в теории струн. Хотя сильновзаимодействующая десятимерная теория суперструн выглядит трудноразрешимой, дуальное описание автоматически перестраивает ее в теорию, в которой можно использовать теорию возмущений. Расчеты, трудные в одной теории, становятся выполнимыми в другой. Даже если константа связи в одной теории слишком велика для того, чтобы использовать теорию возмущений, в другой она оказывается достаточно малой, что позволяет проводить вычисления по теории возмущений. Однако мы еще не до конца понимаем дуальность. Например, никто не знает, как вычислить что-нибудь, когда константа взаимодействия струны не слишком мала и не слишком велика. Но когда одна из констант очень мала или очень велика (а другая константа, соответственно, очень велика или очень мала), то расчеты можно осуществить.
Дуальность сильновзаимодействующей теории суперструн и слабовзаимодействующей одиннадцатимерной теории супергравитации утверждает, что можно вычислить все, что вам только хочется знать в сильновзаимодействующей десятимерной теории суперструн, совершив вычисления в рамках теории, которая кажется на первый взгляд совершенно иной. Все, что предсказывается сильновзаимодействующей десятимерной теорией суперструн, может быть получено и из слабовзаимодействующей одиннадцатимерной теории супергравитации, и наоборот.
Свойство этой дуальности, которое делает ее столь невероятной, заключается в том, что оба описания включают только локальные взаимодействия, т. е. взаимодействия с соседними объектами. Даже если соответствующие объекты существуют в обоих описаниях, дуальность только тогда становится поистине удивительным и интересным явлением, если оба описания содержат локальные взаимодействия. В конце концов, измерение — это больше, чем собрание точек, это способ организации вещей по тому, насколько они близки или удалены друг от друга. Компьютерная распечатка может содержать все, что я хочу знать, и быть эквивалентной организованному множеству файлов или документов, но она не станет простым описанием, пока информация не будет логически связана с соседней. Локальные взаимодействия как в десятимерной теории суперструн, так и в одиннадцатимерной теории супергравитации, — это то, что делает размерности в обоих теориях, а следовательно и сами теории, полными смысла и пользы.
Эквивалентность между десятимерной теорией суперструн и одиннадцатимерной супергравитацией доказали Пол Таунсенд из Кембриджа и Майкл Дафф из Техасского аграрно-механического университета. В течение долгого времени многие теоретики-струнники резко возражали и охаивали их работу по одиннадцатимерной супергравитации. Они не могли понять, почему Дафф и Таунсенд тратят свое время на эту теорию, когда совершенно очевидно, что физикой будущего является теория струн. После доклада Виттена теоретики-струнники должны были признать, что одиннадцатимерная супергравитация не просто интересна, она эквивалентна теории струн!
Я осознала, какой большой интерес вызвал этот удивительный результат про дуальность, во время полета из Лондона домой. Пассажир, оказавшийся рок-музыкантом, увидел, что я читаю какие-то статьи по физике. Он подошел ко мне и спросил, является ли вселенная десяти- или одиннадцатимерной. Я несколько удивилась. Но ответила и объяснила, что в определенном смысле она и такая, и другая. Так как десяти- и одиннадцатимерные теории эквивалентны, каждую из них можно считать правильной. Соглашение приписывает вселенной то число измерений, которое соответствует теории со слабовзаимодействующими струнами, а следовательно, с меньшим физическим значением константы связи струны.
Но в противоположность константам, связанным с взаимодействиями Стандартной модели, интенсивность которых мы можем измерить, нам до сих пор неизвестна величина константы связи струны. Она может быть слабой, и в этом случае можно непосредственно применять теорию возмущений; она может быть сильной, и в этом случае вам лучше использовать теорию возмущений в дуальном описании. Без знания величины константы связи струны у нас нет способа узнать, какое из двух описаний (если вообще какое бы то ни было) есть простейший путь к описанию теории струн в применении к нашему миру[135].
На конференции «Струны-95» были еще кое-какие дуальные сюрпризы. До тех пор большинство теоретиков-струнников полагали, что существуют пять версий теории суперструн, каждая из которых содержит разные взаимодействия. На конференции Виттен (и до него Таунсенд и другой британский физик Крис Халл) доказали дуальность между парами версий теории суперструн. А в течение 1995–1996 годов теоретики-струнники показали, что все эти версии десятимерных теорий дуальны друг другу и, кроме того, дуальны одиннадцатимерной супергравитации. Доклад Виттена вызвал настоящую дуальную революцию. Было показано, что при дополнительном учете свойств бран пять кажущихся различными теорий суперструн являются одной и той же теорией под разными масками.
Так как разные версии теории струн на самом деле совпадают, Виттен сделал вывод, что должна существовать единая теория, включающая одиннадцатимерную супергравитацию и различные проявления теории струн, содержат ли они при этом только слабые взаимодействия или нет. Он назвал новую одиннадцатимерную теорию М-теорией, и я упоминала о ней в начале этой главы. Из М-теории можно получить любую известную версию теории суперструн. Но кроме того М-теория выходит за пределы известных версий в области, которые нам еще предстоит понять. М-теория обладает потенциалом, позволяющим сформулировать более цельную, согласованную картину суперструн и полностью реализовать возможности теории струн как теории квантовой гравитации. Однако потребуется еще много кусков или структур, прежде чем теоретики-струнники поймут М-теорию достаточно хорошо, чтобы достичь этих целей. Если известные версии теории суперструн — это черепки, найденные на месте археологических раскопок, то М-теория — это искомый таинственный артефакт, который позволит собрать их все воедино. Никто пока не знает, как сформулировать М-теорию наилучшим образом. И теоретики-струнники считают, что это их главная цель.
Еще о дуальности
В этом разделе будет детальнее рассмотрена упоминавшаяся выше дуальность между десятимерной теорией суперструн и одиннадцатимерной супергравитацией. Далее этот материал не будет использоваться, так что при желании этот раздел можно опустить и перейти к следующей главе. Однако это книга о размерностях, поэтому небольшое отступление о дуальности между двумя теориями с разными размерностями выглядит вполне уместным.
Свойство, обосновывающее применение дуальности, заключается в том, что одна из двух теорий всегда содержит сильновзаимодействующие объекты. Если взаимодействия сильны, то непосредственно вывести физические следствия теории удается только в редких случаях. Конечно, странно полагать, что десятимерная теория лучше описывается другой, совершенно непохожей одиннадцатимерной теорией, но странность отходит на второй план, если вспомнить, что десятимерная теория содержит такие сильновзаимодействующие объекты, что вы ничего не можете предсказать о том, что происходило вначале.
Тем не менее существует много неясных моментов относительно дуальности между теориями с разным числом измерений. В частном случае дуальности между десятимерной теорией суперструн и одиннадцатимерной супергравитацией на первый взгляд кажется, что существует очень фундаментальная проблема. Десятимерная теория суперструн содержит струны, в то время как в одиннадцатимерной супергравитации струн нет.

Для разрешения этой загадки физики использовали браны. Даже несмотря на то что одиннадцатимерная супергравитация не содержит струны, она содержит 2-браны. Но в противоположность струнам, имеющим только одно пространственное измерение, 2-браны имеют два измерения (как вы могли уже догадаться). Предположим теперь, что одно из одиннадцати измерений свернуто в очень маленькую окружность. В этом случае 2-брана, которая окружает свернутое круговое измерение, выглядит как струна. При этом кажется, что свернутая брана имеет только одно пространственное измерение (рис. 69). Это означает, что одиннадцатимерная теория супергравитации со свернутым измерением выглядит так, как если бы она содержала струны, несмотря на то, что исходная одиннадцатимерная теория их не содержала.
Это может показаться жульничеством, так как ранее мы уже выяснили, что теория со свернутым измерением всегда выглядит как содержащая меньшее число измерений на больших расстояниях и при малых энергиях, поэтому не следует удивляться, что одиннадцатимерная теория со свернутым измерением ведет себя как десятимерная теория. Если вы хотите показать, что десяти- и одиннадцатимерная теории эквивалентны, совсем неясно, почему достаточно изучить одиннадцатимерную теорию, когда одно из измерений свернуто?
Ключ к ответу состоит в том, что в гл. 2 было только показано, что свернутое измерение невидимо на больших расстояниях или при малых энергиях. На конференции «Струны-95» Эдвард Виттен пошел дальше. Он продемонстрировал эквивалентность десяти- и одиннадцатимерной теорий, показав, что одиннадцатимерная теория супергравитации с одним свернутым измерением полностью эквивалентна десятимерной теории суперструн даже на малых расстояниях. Когда измерение свернуто, вы все еще можете различать точки в разных местах вдоль этого измерения, если будете смотреть с очень близкого расстояния. Виттен показал, что в дуальных теориях все эквивалентно, даже те частицы, которые обладают достаточной энергией, чтобы исследовать расстояния, меньшие чем размер свернутого измерения.
Все в одиннадцатимерной теории супергравитации со свернутым измерением, даже малые расстояния и процессы при высоких энергиях, имеет двойников в десятимерной теории суперструн. Более того, дуальность выполняется для измерения, свернутого в окружность любого, неважно какого размера. Раньше, когда мы исследовали свернутое измерение, мы приводили доводы, что не замечено будет только маленькое свернутое измерение.
Но как могут быть одинаковыми теории с разным числом измерений? В конце концов, число измерений пространства есть число координат, необходимых для задания положения точки. Дуальность может быть верна только в случае, если теория суперструн всегда использует дополнительное число для описания точечноподобных объектов.
Ключ к пониманию дуальности заключается в том, что в теории суперструн имеются особые новые частицы, для однозначной идентификации которых требуется задать импульс в девяти пространственных измерениях, а также значение заряда. А в одиннадцатимерной супергравитации нужно знать импульс в десяти пространственных измерениях. Обратите внимание, что хотя есть девять измерений в одном случае и десять в другом, в обоих случаях нужно задать десять чисел: девять значений импульса и заряд в одном случае, десять значений импульса — в другом.
Обычные незаряженные струны не образуют пар с объектами в одиннадцатимерной теории. Так как вам нужно знать одиннадцать чисел, чтобы локализовать объект в пространстве-времени одиннадцатимерной теории, только частицы, несущие заряд, имеют одиннадцатимерных напарников. А партнерами объектов в одиннадцатимерной теории частиц оказываются браны, а именно, заряженные точечноподобные браны, называемые D0-браны. Теория струн и одиннадцатимерная супергравитация дуальны, так как для каждой D0-браны с данным зарядом в десятимерной теории суперструн[136] существует соответствующая частица с определенным одиннадцатимерным импульсом, и наоборот. Объекты десяти- и одиннадцатимерной теорий (а также их взаимодействия) в точности образуют пары.
Хотя может показаться, что заряд сильно отличается от импульса в некотором направлении, если каждый объект с данным импульсом в одиннадцатимерной теории соответствует объекту с конкретным зарядом в десятимерной теории (и наоборот), то дело вкуса — называть ли это число импульсом или зарядом. Число измерений есть число независимых направлений импульса, т. е. число различных направлений, по которым может двигаться объект. Но если импульс вдоль одного из направлений можно заменить зарядом, число измерений не очень хорошо определено. Лучший выбор определяется заданием величины константы связи струны.
Эта поразительная дуальность была одним из первых исследований, в котором браны оказались полезными. Браны стали дополнительными составными частями, которые потребовались для того, чтобы разные теории струн согласовывались друг с другом. Но решающее свойство бран в теории струн, являющееся важным для их приложения в физических теориях, заключается в том, что они могут стать приютом для частиц и взаимодействий. В следующей главе мы объясним это свойство.
Что стоит запомнить
• Теория струн — несоответствующее название. Теория струн содержит также многомерные браны. D-браны — это тип бран в теории струн, на которых должны оканчиваться открытые струны (т. е. струны, не замыкающиеся на себя).
• Браны играют важную роль во многих исследованиях по теории струн в последнем десятилетии.
• Браны важны при демонстрации дуальности, которая показывает, что внешне разные версии теории струн на самом деле эквивалентны.
• При низких энергиях десятимерная теория суперструн дуальна одиннадцатимерной супергравитации — теории, содержащей суперсимметрию и гравитацию. Частицы в одной теории соответствуют бранам в другой.
• Свойства бран, изложенные в данной главе, не будут использоваться далее. Однако они объясняют то воодушевление, которое царило среди специалистов по теории струн.
Глава 16
Неугомонные пассажи: миры на бране
Welcome to where time stands still.
No one leaves and по one will
Metallica[137]
Икар III все больше разочаровывался в Небесах. Он полагал, что это должно быть либеральное и снисходительное общество. Но, вопреки ожиданиям, игра была запрещена, трофеи запрещены, и даже курение уже не разрешалось, самое сильное из всех ограничение состояло в том, что Небеса были прикреплены к Небесной бране; ее жителям запрещалось путешествовать в пятом измерении.
Каждый обитатель Небесной браны знал о пятом измерении и о существовании других бран. В действительности, благочестивые жители небесной браны часто перешептывались об отвратительных типах, заключенных на Тюремной бране, которая была совсем неподалеку. Однако жители Тюремной браны не могли слышать измышлений, которые распространяли о них жители Небесной браны, так что и в балке, и на бранах все было тихо и мирно.
С точки зрения «дуальной революции» может показаться, что браны явились большим благом для исследователей, пытающихся связать теорию струн с видимой Вселенной. Если все различные формулировки теории струн были по существу один и тем же, физикам уже не нужно было мучиться над задачей о поиске правил, с помощью которых природа сделала свой выбор. Нет нужды отдавать предпочтение какой-либо одной теории струн, если они все, несмотря на разные обличья, на самом деле одинаковы.
Но как бы ни было приятно думать, что мы приблизились к открытию связи между теорией струн и Стандартной моделью, все не так просто. Хотя браны необходимы для дуальностей, уменьшающих число явных проявлений теории струн, они на самом деле увеличивают число способов, которыми может возникнуть Стандартная модель. Дело в том, что браны могут приютить частицы и взаимодействия, которые не принимались во внимание теоретиками-струнниками при первоначальном построении теории струн. Из-за большого числа возможностей в отношении того, сколько существует типов бран и где они расположены в многомерном пространстве теории струн, потенциально существует много новых способов реализации Стандартной модели в теории струн, о которых никто еще не помышлял. Взаимодействия в Стандартной модели не обязательно возникают из единственной фундаментальной струны, вместо этого, они могут быть новыми взаимодействиями, возникающими из струн, растянутых между различными бранами. Хотя дуальности утверждают, что исходные пять вариантов теории суперструн эквивалентны, число мыслимых миров на бранах в теории струн громадно.
Похоже, что поиск единственного кандидата на Стандартную модель ничуть не упростился. Когда это стало понятно, эйфория теоретиков-струнников в отношении дуальности утихла. Однако те из нас, кто занимался поиском новых идей для объяснения наблюдаемой физики, парили в небесах. С учетом новых возможностей прикрепления частиц и взаимодействий к бранам, настало время пересмотреть исходные позиции физики частиц.
Свойство бран, важное для их потенциально наблюдаемых приложений, состоит в том, что они могут удерживать частицы и взаимодействия. Цель этой главы — дать читателю представление о том, как это происходит. Мы начнем с объяснения того, почему браны теории струн удерживают частицы и взаимодействия. Мы рассмотрим идею мира на бране, а также первый известный мир на бране, который был выведен из дуальности и теории струн. В последующих главах мы обратимся к тем вопросам миров на бранах и их потенциальных физических приложений, которые я считаю наиболее интересными.
Частицы, струны и браны
Как выразилась Рут Грегори, специалист по общей теории относительности из Даремского университета, браны в теории струн возникают «полностью заправленными» частицами и взаимодействиями. Это означает, что на некоторых бранах уже имеются захваченные частицы и взаимодействия. Как домашние кошки, которые никогда не рискуют покидать стены своего жилища, те частицы, которые прикреплены к бранам, никогда не рискуют отойти от них. Они не могут сделать этого. Их существование определяется существованием бран. Когда частицы движутся, это происходит только вдоль пространственных измерений браны; когда они взаимодействуют, они делают это только на пространственных измерениях, охваченных браной. С точки зрения частиц на бране, если бы не было гравитации и частиц в балке, с которыми они могут взаимодействовать, мир мог бы иметь только измерения на бране.
Теперь посмотрим, каким образом теория струн способна удерживать частицы и взаимодействия на бранах. Представим, что существует только одна D-брана, висящая во вселенной с большим числом измерений. Так как, по определению, оба конца открытой струны должны находиться на единственной D-бране, эта брана будет тем местом, где начинаются и заканчиваются все открытые струны. Концы каждой открытой струны не будут прикреплены в каком-то определенном месте, но будут обязаны лежать где-то на бране. Как рельсы поезда, удерживающие колеса, но позволяющие им катиться, браны действуют как фиксированные поверхности, на которых закреплены концы струны, но по которым, тем не менее, эти концы могут двигаться.
Так как колебательные моды открытых струн — это частицы, то моды открытой струны, у которой оба конца закреплены на бране, — это частицы, закрепленные на этой бране. Такие частицы могут двигаться и взаимодействовать только вдоль измерений, охваченных браной.
Оказывается, что одной из таких частиц, возникающих из связанной на бране струны, является калибровочный бозон, способный переносить взаимодействие.
Мы знаем это, так как спин такой частицы равен спину калибровочного бозона (т. е. 1) и так как он взаимодействует именно так, как это должен делать калибровочный бозон. Такой связанный браной калибровочный бозон будет переносить взаимодействие, которое будет воздействовать на другие связанные с браной частицы, причем, как показывают вычисления, в результате этого взаимодействия частицы на принимающем конце всегда заряжаются. Фактически, конечная точка любой струны, оканчивающейся на бране, будет действовать как заряженная частица. Наличие связанного с браной взаимодействия и этих заряженных частиц говорит о том, что D-брана теории струн возникает «загруженной» заряженными частицами и действующим между ними взаимодействием.
В системах, содержащих более одной браны, возникнет больше взаимодействий и заряженных частиц. Например, пусть имеются две браны. В этом случае, в дополнение к частицам, прикрепленным к каждой бране, появился бы новый тип частиц, возникших из струн, два конца которых находятся на двух различных бранах (рис. 70).

Оказывается, что если две браны отделены друг от друга в пространстве, частицы, связанные со струной, натянутой между ними, будут тяжелыми. Масса частицы, возникающей из колебательных мод такой струны, растет с расстоянием между бранами. Эта масса напоминает энергию, которая накапливается, когда вы растягиваете пружину, — чем больше растяжение, тем больше энергии в ней содержится. Аналогично, легчайшая частица, возникающая из растянутой между двумя бранами струны, будет иметь массу, растущую пропорционально расстоянию между бранами.
Однако когда пружина находится в состоянии покоя, она не запасает никакой энергии. Аналогично, если две струны не разделены, т. е. если они находятся в одном месте, тогда легчайшая частица, возникающая от струны с началом и концом на разных бранах, будет безмассовой.
Предположим теперь, что две браны совмещаются, так что они образуют какие-то безмассовые частицы. Одной из этих безмассовых частиц будет калибровочный бозон, не один из тех калибровочных бозонов, возникших из струн с обоими концами на единственной бране, а совсем другой, новый. Этот новый безмассовый калибровочный бозон, возникающий только при совмещении бран, переносит взаимодействие, действующее на частицы каждой или обеих бран. Кроме того, как и в случае со всеми другими взаимодействиями, взаимодействия на бране связаны с симметрией. В этом случае преобразование симметрии будет менять местами обе браны.
Конечно, если бы две браны действительно были в одном месте, вы могли бы подумать, что довольно странно относиться к ним как к двум разным объектам. И вы были бы правы: если две браны находятся в одном и том же месте, вы можете с полным основанием считать их за одну брану. Такая новая брана существует в теории струн. Она представляет собой тайком совпавшие две браны, и имеет те свойства, которые такие браны должны иметь. На этой бране живут все

Типы частиц, которые мы обсуждали выше: частицы, возникающие от открытых струн, кончающихся на каждой бране в исходном описании с двумя бранами, а также струны, оба конца которых находятся на одной бране.
Теперь представьте, что накладываются мною бран. Тогда появятся много новых типов открытых струн, так как разными концами струна может быть прикреплена к любой из бран (рис. 71). Открытые струны, натянутые между разными бранами, или струны, начинающиеся или кончающиеся на любой одиночной бране, приводят к появлению новых частиц, составленных из колебательных мод этих струн. И опять эти новые частицы включают новые типы калибровочных бозонов и новые типы заряженных частиц. И снова новые взаимодействия ассоциируются с новыми симметриями, меняющими местами различные наложенные друг на друга браны.
Итак, браны возникают «нагруженными» взаимодействиями и частицами; много бран означает богатство возможностей. Кроме того, могут возникать и более тонкие ситуации, включающие разделенные группы бран. Находящиеся в разных местах браны будут нести на себе совершенно независимые частицы и взаимодействия. Частицы и взаимодействия, удерживаемые одной группой бран, будут полностью отличаться от частиц и взаимодействий, удерживаемых другой группой.
Например, если частицы, из которых мы состоим, вместе с электромагнитным взаимодействием все удерживаются на одной бране, мы будем испытывать электромагнитное взаимодействие. Однако с частицами, удерживаемыми на далеких бранах, этого не случится; далекие частицы нечувствительны к электромагнитному взаимодействию. С другой стороны, частицы, удерживаемые на далеких бранах, могут испытывать новые взаимодействия, к которым мы полностью нечувствительны.
Важное свойство подобной системы, которое понадобится позднее, состоит в том, что частицы на разделенных бранах не взаимодействуют друг с другом непосредственно. Взаимодействия локальны: они могут происходить только между частицами в одном и том же месте; частицы на разделенных бранах слишком удалены друг от друга, чтобы взаимодействовать непосредственно.
Можно сравнить балк, полное многомерное пространство, с огромным теннисным стадионом, на котором повсюду происходят отдельные матчи. Мяч на каждом из кортов перелетает туда и обратно через сетку и может двигаться везде по корту. Однако каждый матч происходит отдельно от других, а каждый мяч остается на своем собственном изолированном корте. Точно так же, как мяч на данном корте должен оставаться на нем и только два игрока на этом корте имеют право доступа к мячу, удерживаемые на бранах калибровочные бозоны или другие удерживаемые на бранах частицы взаимодействуют только с объектами на своей собственной бране.
Однако частицы на разделенных бранах могут взаимодействовать друг с другом, если существуют частицы и взаимодействия, которые могут свободно перемещаться по балку. Такие частицы в балке должны иметь возможность заходить на брану и покидать ее. Изредка они могут взаимодействовать с частицами на бране, но они могут также свободно перемещаться в полном пространстве большего числа измерений.
Система с разделенными бранами и взаимодействующими с ними частицами в балке напоминает стадион с разными одновременно происходящими матчами, в которых игроки в разных играх имеют одного и того же тренера. Тренер, который должен присматривать, что происходит в разных играх в одно и то же время, будет передвигаться от одного корта к другому. Если один игрок хочет что-то сообщить игроку на другом корте, он может передать сообщение тренеру, который передаст его другому игроку. Сами игроки не будут непосредственно взаимодействовать во время своих матчей, но тем не менее они могут связаться через человека, перемещающегося между соответствующими кортами. Аналогично, частицы в балке могут взаимодействовать с частицами на одной бране, а затем — с частицами на далекой бране, позволяя таким образом косвенно взаимодействовать частицам, прикрепленным к разделенным бранам.
В следующем разделе мы увидим, что гравитон, частица, переносящая гравитационное взаимодействие, является одной из таких живущих в балке частиц. В системе с большим числом измерений он будет перемещаться по всему пространству большого числа измерений и взаимодействовать со всеми частицами везде, независимо от того, находятся они на бранах или нет.
Гравитация: опять иная
В противоположность всем другим взаимодействиям, гравитация никогда не захватывается на брану. Связанные с браной калибровочные бозоны и фермионы являются результатом открытых струн; но в теории струн гравитон, частица, переносящая гравитационное взаимодействие, есть мода замкнутой струны. У замкнутых струн нет концов, и поэтому им нечем зацепиться за брану.
Частицы, являющиеся колебательными модами замкнутых струн, имеют неограниченное разрешение на перемещение в полном многомерном пространстве-времени. Гравитационное взаимодействие, которое, как мы знаем, передается частицей замкнутой струны, в очередной раз оказывается выделенным по сравнению с другими взаимодействиями. В противоположность калибровочным бозонам или фермионам, гравитон должен распространяться в полном многомерном пространстве-времени. Не существует способа связать гравитацию в пространстве с меньшим числом измерений. В следующих главах мы увидим, что, как это ни поразительно, гравитация может быть локализована вблизи браны. Но связать гравитацию на бране не под силу никому.
Это означает, что хотя миры на бранах могут захватывать большинство частиц и взаимодействий, они никогда не смогут захватить гравитацию. Это очень хорошее свойство. Оно говорит нам, что миры на бранах будут всегда включать многомерную физику, даже если вся Стандартная модель будет привязана к четырехмерной бране. Если существует мир на бране, все на нем будет продолжать взаимодействовать с гравитацией, а гравитация будет проявляться везде в полном многомерном пространстве. Вскоре мы увидим, как это важное различие между гравитацией и другими взаимодействиями помогает объяснить, почему гравитация настолько слабее других известных взаимодействий.
Модельные миры на бранах
Очень скоро после того, как физики заметили важность бран для теории струн, браны стали объектом интенсивных исследований. В частности, физикам очень хотелось понять возможное значение бран для физики частиц и нашей концепции вселенной. На сегодняшний день теория струн не говорит нам, существуют ли браны во вселенной и если существуют, то в каком количестве. Мы знаем только, что браны являются важным теоретическим разделом теории струн, без которого эта теория неполна. Но если мы знаем, что браны есть часть теории струн, сразу же возникает вопрос, могут ли они существовать в реальном мире. И если они существуют, то каковы следствия?
Возможность существования бран открывает много новых вариантов состава вселенной, причем некоторые из них могут иметь отношение к физическим свойствам наблюдаемой нами материи. Теоретик-струнник Аманда Пит, услышав слова Рут Грегори о «полностью заправленных» бранах, заметила, что браны «расчистили поле для построения основанных на струнах моделей». После 1995 года браны стали новым инструментом построения моделей.
К концу 1990-х годов многие физики, в том числе и я, расширили область своих исследований, включив возможность существования бран. Мы спрашивали себя: «Что, если существует вселенная с дополнительными измерениями, в которой известные нам частицы и силы не перемещаются во всех измерениях, а ограничены меньшим числом измерений, захвачены на брану с меньшим числом измерений?»
Сценарии с участием бран предлагали много новых возможностей для глобальной структуры пространства-времени. Если частицы Стандартной модели захвачены на брану, это же касается и нас самих, так как мы и окружающий нас космос состоим из этих частиц. Кроме того, не все частицы должны находиться на одной и той же бране. Поэтому должны существовать совершенно новые и незнакомые частицы, подверженные влиянию отличных от известных нам взаимодействий. Наблюдаемые нами частицы и взаимодействия могут быть лишь малой частью значительно большей вселенной. Два физика из Корнеллского университета, Генри Тай и Зураб Какушадзе, предложили для таких сценариев термин «миры на бранах». Генри говорил мне, что он использовал этот термин для того, чтобы одним махом описать все многочисленные способы, которыми вселенная могла включать браны, не отдавая предпочтения никакой конкретной возможности.
Хотя быстрое размножение числа возможных миров на бранах может разочаровать теоретиков-струнников, пытающихся построить одну единственную теорию мира, оно очень захватывает. Мы имеем много реальных возможностей для мира, в котором живем, и одна из них может действительно описывать этот мир. Так как во вселенной с дополнительными измерениями законы физики частиц будут немного отличаться от тех, которые предполагали физики-частичники, дополнительные измерения открывают новые способы для исследования загадочных свойств Стандартной модели. Хотя эти идеи во многом спекулятивны, миры на бранах, исследующие проблемы физики частиц, скоро можно будет проверить в экспериментах на коллайдерах. Это означает, что опыт, а не наши предубеждения, может окончательно решить, применимы ли эти идеи к нашему миру.
Мы собираемся исследовать некоторые из этих новых миров на бранах. Мы зададимся вопросом, на что они похожи и к каким следствиям это приводит. Мы не будем ограничиваться мирами на бранах, явно выведенными из теории струн, а рассмотрим модельные миры на бранах, которые уже принесли новые идеи в физику частиц. Физики настолько далеки от понимания приложений теории струн, что было бы преждевременным исключать модели только потому, что никто еще не нашел примера теории струн с конкретным набором частиц или взаимодействий, или конкретным распределением энергии. Такие миры на бранах следует рассматривать как мишени для исследования теории струн. На самом деле модель закрученной иерархии, о которой я говорю в гл. 20, была выведена из теории струн только после того, как Раман Сундрум и я предложили ее как возможный мир на бране.
В последующих главах будет представлено несколько различных миров на бранах. Каждый из них будет иллюстрировать совершенно новое физическое явление. Первый мир на бранах покажет, каким образом миры на бранах могут избежать анархического принципа. Второй покажет, что измерения могут быть много больше, чем мы ранее полагали; третий покажет, что пространство-время может быть настолько искривлено, что можно ожидать появления объектов с совершенно разными размерами и массами; наконец, последние два покажут, что даже бесконечные дополнительные измерения могут быть невидимыми, если пространство-время искривлено, и что пространство-время может даже казаться имеющим разные размерности в разных местах.
Я представляю несколько моделей, так как все они соответствуют реальным возможностям. Но не менее важно, что каждая из них содержит некоторое новое свойство, о котором до недавнего времени физики думали как о немыслимом. В конце каждой главы я резюмирую значение каждой модели и то, как она нарушает общепринятые взгляды. При желании вы можете прочесть эти помеченные маркером выводы и получить общую картину, краткое резюме значения той конкретной модели, которая объясняется в тексте главы.
Прежде чем приступать к описанию этих миров на бранах, я кратко опишу первый известный мир на бранах, выведенный непосредственно из теории струн. Петр Хоржава и Эдвард Виттен натолкнулись на этот мир на бранах (по инициалам авторов названный ХВ-мир), изучая дуальность в теории струн. Я представляю эту модель, так как она не только интересна сама по себе, но и обладает рядом свойств, являющихся предвестником свойств других миров на бранах, с которыми мы вскоре столкнемся.
Теория Хоржавы — Виттена
Мир на бранах ХВ изображен на рис. 72. Это одиннадцатимерный мир с двумя параллельными бранами, каждая из которых имеет девять пространственных измерений и ограничивает пространство балка с десятью пространственными измерениями (всего одиннадцать пространственно-временных измерений). Вселенная ХВ была первой теорией мира на бранах; в мире ХВ каждая из двух бран содержит разные наборы частиц и взаимодействий.

Взаимодействия на двух бранах те же, что и у гетеротической струны, введенной в гл. 14; это была построенная Дэвидом Гроссом, Джеффом Харви, Эмилем Мартинесом и Райаном Ромом теория, в которой колебания, движущиеся вдоль струны направо и налево, взаимодействуют по-разному. Половина этих взаимодействий закреплена на одной из двух граничных бран, другая половина — на другой. На каждой из двух бран удерживается достаточно взаимодействий и частиц, чтобы любая брана в принципе могла содержать все частицы Стандартной модели (и следовательно нас). Хоржава и Виттен предположили, что частицы и взаимодействия Стандартной модели расположены на одной из двух бран, а гравитация и другие частицы, являющиеся частью теории, но которые мы никогда не наблюдали в нашем мире, могут свободно путешествовать по другой бране или вне бран в полном одиннадцатимерном балке.
На самом деле мир на бранах ХВ не просто имел те же взаимодействия, что и гетеротическая струна, — он и был гетеротической струной, хотя и с сильной константой связи струны. Это еще один пример дуальности. В этом случае одиннадцатимерная теория с двумя бранами, ограничивающими одиннадцатое измерение (десятое пространственное), дуальна десятимерной гетеротической струне. Иначе говоря, когда взаимодействия гетеротической струны очень сильны, теория лучше описывается как одиннадцатимерная теория с двумя граничными бранами и девятью пространственными измерениями. Это напоминает обсуждавшуюся в предыдущей главе дуальность между десятимерной теорией суперструн и одиннадцатимерной супергравитацией. Но в нашем текущем примере одиннадцатое измерение не свернуто, а, напротив, ограничено двумя бранами. Повторим еще раз, что одиннадцатимерная теория может быть эквивалентной десятимерной, хотя в одной теории есть сильные взаимодействия, а в другой есть слабые.
Конечно, даже если частицы Стандартной модели захвачены на брану, теория будет все еще иметь больше измерений, чем мы видим вокруг. Если мир на бранах ХВ должен соответствовать реальности, шесть его измерений должны быть невидимы. Хоржава и Виттен предположили, что шесть измерений свернуты в крохотное многообразие Калаби — Яу.
Если шесть измерений свернуты, о вселенной ХВ можно думать как о пятимерной эффективной теории с четырехмерными граничными бранами. Такая картина пятимерной вселенной с двумя граничными бранами интересна и исследовалась многими физиками. Раман и я применили определенную технику, которую Берт Оврут и Дэн Уолдрам использовали для изучения эффективной теории ХВ, к различным пятимерным теориям, о которых я расскажу в гл. 20 и 22.
Одно поразительное свойство мира на бранах ХВ заключается в том, что он может включить в себя не только частицы и взаимодействия Стандартной модели, но также и полную теорию Великого объединения. Поскольку гравитация берет начало в высших измерениях, оказывается возможным, что гравитация и другие взаимодействия будут иметь в этой модели одинаковые константы при высоких энергиях.
Мир на бранах ХВ иллюстрирует три причины, благодаря которым миры на бранах могут иметь отношение к физике в реальном мире. Во-первых, он включает более одной браны. Это означает, что он может содержать взаимодействия и частицы, взаимодействующие друг с другом только слабо из-за расстояния между двумя бранами, на которых они закреплены. Частицы, удерживаемые на разных бранах, могут сообщаться друг с другом только через общие взаимодействия с частицами в балке. Это первое свойство окажется важным в моделях секвестирования, которые мы рассмотрим в следующей главе.
Второе важное свойство мира на бранах заключается в том, что любой мир на бранах вводит в физику новые масштабы длины. Эти новые масштабы, например размер дополнительных измерений, могут иметь отношение к объединению взаимодействий или проблеме иерархий. Проблемы в каждой из этих теорий сосредоточены вокруг вопроса о том, почему в единой теории должны быть настолько различные энергетические и массовые масштабы и почему квантовые эффекты не стремятся их сгладить.
Наконец, браны и балк могут нести энергию. Эта энергия может быть запасена в бранах и в многомерном балке; она не зависит от присутствия частиц. Как и все формы энергии, эта энергия искривляет пространство-время балка. Скоро мы увидим, что такая кривизна пространства-времени, вызванная распределенной повсюду в пространстве энергией, может быть очень важной для миров бран.
Мир бран Хоржавы — Виттена, безусловно, имеет много поразительных свойств. Однако он также испытывает трудности, которые, по-видимому, присущи всем реализациям теории струн при воспроизведении известной физики. Теорию ХВ очень трудно проверить экспериментально, так как ее измерения очень малы. Многие невидимые частицы должны быть достаточно тяжелыми, чтобы избежать детектирования, а шесть измерений теории должны быть свернуты, хотя ни размер, ни форма свернутых измерений пока что не определены.
Следуя таким путем, можно случайно наткнуться на версию теории струн, правильно описывающую природу; такую возможность полностью исключить нельзя. Однако для этого нам действительно должно очень повезти. Но проблемы физики частиц также требуют к себе внимания, и стоит исследовать, как их можно решить в мире с дополнительными пространственными измерениями и бранами, простирающимися только вдоль некоторых их них. Этому посвящена оставшаяся часть книги.
Что стоит запомнить
• Миры на бранах возможны в рамках теории струн. Частицы и взаимодействия в теории струн могут захватываться на браны.
• Гравитация отлична от всех других взаимодействий. Она никогда не захватывается браной и всегда распространяется вдоль всех измерений.
• Если теория струн описывает вселенную, она может содержать много бран. В этом смысле миры на бранах очень естественны.
V Схемы для вселенных с дополнительными измерениями
Глава 17
Редконаселенные пассажи: мультивселенные и уединение
Just turn around now
(cause) you’re not welcome anymore.
Gloria Gaynor[138]
Несмотря на действующий на небесной бране полный запрет на азартные игры, Икар III все-таки не удержался. Он проигнорировал несколько предупреждений, поэтому его приговорили к заключению на Тюремной бране, далекой бране, отделенной от Небесной браны пятым измерением. Но даже находясь в заключении, он упорно пытался установить контакты со своими прежними дружками. Однако расстояние между двумя бранами делало общение затруднительным. Ему приходилось подолгу голосовать, чтобы привлечь внимание почтальонов, разносивших почту по балку, ибо многие почтальоны игнорировали его мольбы. Те немногие, кто останавливались, всегда доставляли его послания на небесную брану, хотя скорость доставки была удручающе малой.
Тем временем на Небесной бране начались беспорядки. Ангелы-хранители, которые так храбро спасли иерархию, не испытывали никакого уважения к семейным ценностям других обитателей и были на грани создания межпоколенческой нестабильности. падшие небесные ангелы считали приемлемыми любые пары и поощряли всех к помолвкам с партнерами из другого поколения.
Когда Икар осознал опасность, он был ошеломлен. Он решил непременно исправить ситуацию. Икар понял, что неторопливое общение с Небесной браной, к которому его вынуждали обстоятельства, может сыграть на руку, и позволит постепенно унять непомерную гордыню вышедших из-под контроля ангелов. Вмешательство Икара помогло, и ангелы перестали угрожать общественному порядку. И хотя Икар III по-прежнему должен был отбывать свой срок, избавленные от опасности обитатели небесной браны с тех пор всегда славили его в своих мифах.
Эта глава посвящена понятию уединения, одной из причин, по которым дополнительные измерения могут оказаться важными для физики частиц. Уединенные частицы физически разделены на разных бранах. Если разные частицы помещены в разную окружающую среду, уединение могло бы объяснить определенные свойства, отличающие одну частицу от другой. Уединение могло бы быть причиной, по которой анархический принцип, утверждающий, что все должно взаимодействовать, оказывается не всегда верным. Если частицы разделены в дополнительных измерениях, они не так охотно взаимодействуют друг с другом.
В принципе, частицы могут быть уединены и в трех пространственных измерениях. Но, насколько мы знаем, все направления и все точки в трехмерном пространстве равноправны. Известные законы физики утверждают, что каждая частица может находиться где угодно в наблюдаемых трех измерениях, так что уединение в трех измерениях — это не выход. Однако в многомерном пространстве фотоны и заряженные объекты не обязательно могут находиться где угодно. Дополнительные измерения предлагают способ разделения частиц. Определенные типы частиц могут удерживаться в отдельных областях пространства, занятых разными бранами. Так как не все точки в дополнительных измерениях выглядят одинаково, эти измерения дают способ разделения частиц путем удержания разных типов частиц на разделенных бранах.
Теории, которые уединяют частицы, обладают потенциалом для решения многих проблем. История про Икара относится к моему первому подходу к анализу дополнительных измерений — применению уединения к нарушению суперсимметрии. В то время как четырехмерные теории сталкиваются с серьезными проблемами из-за того, что нарушающие суперсимметрию модели в общем случае содержат нежелательные взаимодействия, уединенные модели с нарушенной суперсимметрией кажутся намного более обещающими. Уединение могло бы также объяснить, почему частицы имеют массы, отличающиеся друг от друга, и почему распад протона не происходит в моделях с дополнительными измерениями. В этой главе мы используем идею уединения и несколько ее приложений к физике частиц. Мы увидим, что даже такие идеи, как суперсимметрия, которая, как мы думали, применима в четырехмерном пространстве-времени, могут быть с большим успехом применены в моделях с дополнительными измерениями.
Мой путь к дополнительным измерениям
Физики — счастливые люди в том плане, что у них много возможностей встречаться на конференциях и делиться с коллегами стимулирующими идеями. Но ежегодно проводится такое ошеломляющее количество конференций и рабочих совещаний по физике частиц, что трудно сделать выбор, какие приглашения принять. Одни конференции — это большие собрания, позволяющие ознакомится с текущими работами других и поделиться вашими последними результатами.
Другие — сравнительно небольшие встречи, на два или три дня, где физики сообщают главные результаты в очень специальной области. Есть также расширенные рабочие совещания, где физики завязывают сотрудничество с коллегами или подводят итоги. Иногда конференции проводятся в таких замечательных местах, что было бы грешно их пропустить.
Хотя Оксфорд — очень приятное место, конференция по суперсимметрии, в которой я принимала участие в начале июля 1998 года, относилась ближе к первой категории. Суперсимметрия, которая в течение многих лет рассматривалась как единственный возможный способ решить проблему иерархии, с течением времени развилась в главную область исследований, так что каждый год физики собирались для того, чтобы обсудить последние достижения в этой области.
Однако на Оксфордской конференции были сюрпризы. Самым интересным разделом оказалась не суперсимметрия, а недавно родившаяся идея о дополнительных измерениях. Один из наиболее стимулирующих докладов был посвящен большим дополнительным измерениям (об этом пойдет речь в гл. 19). Другие доклады были посвящены судьбе дополнительных измерений в теории струн, а также возможным экспериментальным приложениями дополнительных измерений. Новизна и гипотетический характер, подобных идей подчеркивались даже самими названиями докладов. Теоретик из Чикаго Джефф Харви и несколько следующих докладчиков шутливо назвали свои доклады так, что они перекликались с Островом Фантазий. Джо Ликкен, теоретик из Фермилаб, даже приготовил слайд с маленьким человечком с табличкой «Da brane. Da brane». (Нет нужды говорить, что пародия на Татту и его знаменитое приветствии «da plane» на Острове Фантазий была понятна только тем, кто смотрел в семидесятых американское TV.)
Несмотря на шутливый стиль, после этой конференции я стала размышлять о дополнительных измерениях и о том, почему проблемы физики частиц могли быть решены в мире с дополнительными измерениями. Хотя я была скептически настроена в отношении больших дополнительных размерностей, которые были одной из горячих тем для обсуждения, и не планировала сама заниматься ими, я была убеждена, что браны и дополнительные измерения могут служить важными инструментами для построения моделей, способных в принципе объяснить некоторые непонятные явления физики частиц, которые не поддаются простым четырехмерным объяснениям.
В том году я планировала провести остаток лета в Бостоне, хотя это было для меня не характерно; большинство бостонских физиков-теоретиков, включая меня, проводило каждый год большую часть лета в разъездах, принимая участие в разного рода конференциях и рабочих совещаниях. Но я решила остаться дома, отдохнуть и подумать о новых идеях.
Раман Сундрум, который был тогда постдоком в Бостонском университете, также решил провести лето в Бостоне. Мы часто встречались на конференциях или пересекались в моем или его институте. Нам даже пришлось недолго в одно и то же время быть постдоками в Гарварде. Так как Раман уже занимался дополнительными измерениями, я решила, что будет полезно обсудить с ним мои идеи.
У Рамана очень интересный характер. Большинство физиков на ранних стадиях своей научной карьеры работают над сравнительно безопасными проблемами — вопросами общего-характера, в которых они, возможно, достигнут прогресса. Однако Раман определенно хотел сосредоточиться на самом, по его мнению, важном, даже если эта задача была очень сложная или ею мало кто занимался. Несмотря на очевидный талант, такой подход к делу не позволил ему получить работу на факультете и привел на третью постдоковскую позицию. Но в это время Раман думал о дополнительных измерениях и бранах; его интересы начали постепенно совпадать с интересами остальной части физического сообщества.
Наше сотрудничество началось в кафе «У Тосканини» (сейчас к сожалению закрытом) в студенческом центре МТИ, где продавали потрясающее мороженое и очень хороший кофе. Кафе было идеальным местом встречи для свободного обсуждения идей, без помех и ограничений, где одновременно можно было насладиться вкусными вещами.
Начавшись с разговоров за кофе, наше исследование развивалось и выкристаллизовывалось. В августе мы достигли этапа, когда нам стали требоваться доски все большего размера, чтобы иметь перед глазами детали наших обсуждений. Так как доска в моем профессорском офисе в МТИ была довольно маленькой, нам приходилось блуждать по «бесконечному коридору» (очень длинному проходу, идущему вдоль всей длины главного здания МТИ) в поисках пустых аудиторий.
Конкретная исследовательская задача, на которой мы сосредоточились, состояла в применении уединения к нарушению суперсимметрии. Идея состояла в том, чтобы уединить частицы, ответственные за нарушение суперсимметрии, от частиц Стандартной модели, тем самым предотвратив нежелательные взаимодействия между ними (рис. 73). Мы выбрали слово «уединение», для того чтобы отличать модели, в которых частицы разделены на разных бранах, от так называемого «скрытого сектора» моделей нарушения суперсимметрии, которые были в то время модными. В моделях скрытого сектора нарушающие суперсимметрию частицы слабо взаимодействуют с частицами Стандартной модели, но на самом деле не скрыты (несмотря на название), и поэтому могут взаимодействовать способами, неприемлемыми в реальном мире.
Вначале я была очень воодушевлена нашими идеями, а Раман настроен скептически, но с течением времени наши роли менялись. Один энтузиаст и один скептик, мы проделали большую работу и быстро добрались до сути той физики, о которой мы размышляли. Иногда мы даже слишком быстро отвергали идеи, но обычно один из нас достаточно долго держался за идею, чтобы ее хорошо обсудить и продвинуться вперед.


Френсис Бэкон, который вместе с Галилеем считается одним из основателей современного научного метода, говорил, как сложно двигаться вперед, сохраняя скептицизм, необходимый для уверенности в правильности своих результатов. Как воспринимать идею достаточно серьезно для того, чтобы копаться в ее следствиях, и одновременно отдавать себе отчет, что она может оказаться неверной? Отдельный человек, при наличии достаточного времени, может переходить между этими позициями и прийти в конце концов к правильному ответу. Но если два человека занимают противоположные позиции, то часто требуются часы или даже минуты, чтобы отвергнуть ошибочную, хоть и захватывающую идею.
Тем не менее идея, с которой мы стартовали, а именно, уединение, чтобы избежать нежелательных взаимодействий в суперсимметричных теориях, казалась мне достаточно разумной. В четырех измерениях нет действенных механизмов, а дополнительные измерения, похоже, дают все необходимое для построения успешной модели. Однако лишь в конце лета мы осознали идею уединения и ее следствия для нарушения суперсимметрии достаточно хорошо, чтобы выработать общее понимание и сосредоточиться на достоинствах этой идеи.
Естественность и уединение
Причина, по которой идея уединения может оказаться важной, заключается в том, что она позволяет предотвратить проблемы, вызванные анархическим принципом, негласным правилом, утверждающим, что в четырехмерной квантовой теории поля все, что может случиться, случается. Из-за этого теории предсказывают взаимодействия и соотношения между массами, которые не наблюдаются в природе. Даже взаимодействия, не возникающие в классической теории (т. е. в теории, которая не принимает во внимание квантовую механику), появятся сразу, как только будут включены виртуальные частицы; взаимодействия виртуальных частиц приводят ко всем возможным взаимодействиям.
Приведем аналогию, поясняющую, почему это происходит. Предположим, вы сказали Афине, что завтра пойдет снег, а Афина передала это Икару. И хотя вы не общались напрямую с Икаром, тем не менее ваше сообщение повлияет на то, как Икар оденется завтра — из-за вашего виртуального совета он наденет теплую куртку.
Аналогично, если частица взаимодействует с виртуальной частицей, а эта виртуальная частица, в свою очередь, взаимодействует с третьей частицей, то общий эффект заключается в том, что взаимодействуют между собой первая и третья частицы. Анархический принцип говорит нам, что процессы, включающие виртуальные частицы, неизбежно происходят, даже если они не происходят классически. Часто такие процессы индуцируют нежелательные взаимодействия.
Многие проблемы в теориях физики частиц коренятся в анархическом принципе. Например, квантовые вклады в массу хиггсовской частицы, происходящие от виртуальных частиц, являются следствием проблемы иерархии. На любом пути, выбранном хиггсовской частицей, она может быть временно перехвачена тяжелыми частицами, и эти перехваты увеличивают массу хиггсовской частицы.
В гл. 11 мы видели другой пример, включающий анархический принцип. В большинстве теорий с нарушенной суперсимметрией виртуальные частицы индуцируют нежелательные взаимодействия, которые, как мы знаем из экспериментов, на самом деле отсутствуют. Такие взаимодействия вызывали бы превращения среди известных кварков и лептонов. Подобные меняющие аромат взаимодействия либо вообще не происходят в природе, либо происходят очень редко. Если мы хотим, чтобы теория работала, необходимо как-то устранить эти взаимодействия, которые, как утверждает анархический принцип, будут обязательно возникать.
Виртуальные частицы не обязательно приводят к таким нежелательным предсказаниям. В теории не будет нежелательных взаимодействий в том невероятном случае, если произойдут огромные сокращения между классическим и квантовым вкладами в физическую величину. Даже несмотря на то что классические и квантовые вклады по отдельности очень велики, их сумма может, по-видимому, дать приемлемое предсказание. Такой способ позволяет обойти проблему, но почти наверняка это полумера, заменяющая правильное решение. Никто из нас на самом деле не верит, что такие точные случайные сокращения позволяют фундаментальным образом объяснить отсутствие определенных взаимодействий. Но мы используем это как временную подпору, чтобы продвинуться дальше и изучить другие аспекты наших теорий.
Физики полагают, что в теории отсутствуют взаимодействия только в том случае, когда они устранены способом, который можно считать естественным. В повседневной жизни слово «естественный» относится к вещам, происходящим спонтанно, без вмешательства человека. Но для специалистов по физике частиц «естественно» означает больше, чем нечто происходящее; оно означает, что если что-то произойдет, это не будет загадкой. Для физиков «естественно» только ожидать ожидаемое.
Анархический принцип и многие нежелательные взаимодействия, индуцируемые квантовой механикой, говорят нам, что в любую физическую модель, лежащую в основе Стандартной модели, должны войти новые понятия, для того чтобы такая модель имела шансы быть правильной. Одна из причин, по которой симметрии столь важны, заключается в том, что они представляют единственный естественный способ, гарантирующий, что в четырехмерном мире не возникнут нежелательные взаимодействия. Симметрии по существу дают дополнительное правило, согласно которому, по-видимому, возникают взаимодействия. Вы легко поймете это явление с помощью аналогии.
Предположим, что вы накрываете стол на шесть персон, но должны сделать это так, чтобы все шесть столовых приборов были одинаковы. Это означает, что ваша раскладка приборов допускает преобразование симметрии, меняющее местами каждую пару приборов. Без этой симметрии вы могли бы, в принципе, дать одной персоне две вилки, другой три, а кто-то еще получил бы пару китайских палочек для еды. Но с учетом ограничений, накладываемых симметрией, вы можете расставлять приборы только так, что у всех шести персон будет одинаковое количество вилок, ножей, столовых ложек и китайских палочек — вы никогда не сможете дать одной персоне два ножа, а другой три.
Аналогично, симметрии говорят вам, что не все взаимодействия могут возникнуть. Даже если взаимодействуют много частиц, в общем случае квантовые вклады не порождают взаимодействий, нарушающих симметрию, если классические взаимодействия эту симметрию сохраняют. Если вы не начали с нарушающих симметрию взаимодействий, вы никогда не породите такого взаимодействия (не считая известных редких аномалий, упомянутых в гл. 14), даже если вы включите все возможные взаимодействия с участием виртуальных частиц. Требуя симметрии накрытого стола, вы всегда придете к тождественным приборам, независимо от того, сколько раз вы изменили набор, добавляя, например, ложки для грейпфрута или ножи для стейка. Аналогично, взаимодействия, которые несовместимы с симметрией, не будут индуцироваться, даже если принимать во внимание квантово-механические эффекты. Если симметрия не была нарушена в классической теории, то не будет существовать ни одного пути, где бы при движении частицы возникали нарушающие симметрию взаимодействия.
До недавнего времени физики полагали, что симметрии — это единственный способ избежать анархического принципа. Но, как однажды поняли мы с Раманом, наевшись вдоволь мороженого, другим таким способом являются разделенные браны. Главная причина, почему дополнительные измерения показались мне с самого начала столь многообещающими, состояла в том, что они предлагали объяснение, отличное от соображений симметрии, почему ограниченные или необычные типы взаимодействий могли быть естественными. Уединение нежелательных частиц может предотвратить появление нежелательных взаимодействий, так как они в общем случае не возникают между частицами, находящимися на разных бранах.
Частицы на разных бранах не взаимодействуют сильно, так как взаимодействия всегда локальны — непосредственно взаимодействуют только частицы, находящиеся в одном месте. Уединенные частицы могут контактировать с частицами на других бранах, но только если имеются взаимодействующие частицы, которые могут перемещаться от одной браны к другой. Как Икар на Тюремной бране, частицы на разных бранах обладают ограниченными средствами связи друг с другом, так как у них нет никаких иных способов, кроме приглашения посредника. Даже если такие косвенные взаимодействия возникают, они часто оказываются очень малыми, так как промежуточные частицы в балке, в частности, имеющие массу, очень редко перемещаются на большие расстояния.
Это подавление взаимодействий между частицами, уединенными в разных местах, можно сравнить с глушением международной информации в стране, которую я назову Ксенофобией, где правительство внимательно контролирует границы и средства массовой информации. В Ксенофобии не обеспечиваемая локально информация может быть получена только от иностранных гостей, которые ухитряются в нее въехать, или из газет или книг, ввозимых контрабандой.
Аналогично, разделенные браны представляют платформу, опираясь на которую можно обойти анархический принцип, удваивая таким образом набор инструментов в распоряжении у природы для того, чтобы гарантировать отсутствие нежелательных взаимодействий. Еще одним достоинством уединения является то, что оно может даже защитить частицы от эффектов нарушения симметрии. До тех пор пока нарушение симметрии происходит достаточно далеко от этих частиц, оно будет оказывать на них весьма незначительное воздействие. Когда нарушение симметрии уединяется, это напоминает карантин при заразной болезни, когда больному не разрешают свободно перемещаться. Или, возвращаясь к другой аналогии, любые драматические события, происходящие вне Ксенофобии, не окажут никакого влияния на саму страну, если не будет вмешательства извне. Без проницаемых границ Ксенофобия могла бы существовать независимо от остального мира.
Уединение и суперсимметрия
Конкретная проблема, которую мы с Раманом исследовали летом 1998 года, состояла в том, чтобы понять, как уединение могло бы работать в природе, приводя ко вселенной с нарушенной суперсимметрией и со всеми теми свойствами, что мы наблюдаем. Мы видели, что суперсимметрия может изящно защитить иерархию и гарантировать, что все большие квантово-механические вклады в массу хиггсовской частицы дадут при сложении в сумме нуль. Но, как мы видели в гл. 13, даже если суперсимметрия существует в природе, она должна быть нарушена, для того чтобы объяснить, почему мы наблюдаем частицы, но не их суперпартнеров.
К сожалению, большинство моделей с нарушенной симметрией предсказывает взаимодействия, отсутствующие в природе, и такие модели вряд ли могут быть правильными. Раман и я хотели найти физический принцип, который могла бы использовать природа для защиты себя от этих нежелательных взаимодействий, так чтобы с помощью этого принципа мы могли бы улучшить теорию.
Мы сосредоточились на нарушении суперсимметрии в модели мира на бране. Миры на бранах могут сохранять суперсимметрию. Но так же, как в четырех измерениях, суперсимметрия может быть спонтанно нарушена, когда какая-то часть теории содержит частицы, не сохраняющие суперсимметрию. Раман и я поняли, что если все частицы, ответственные за нарушение суперсимметрии, были бы отделены от частиц Стандартной модели, модель с нарушенной суперсимметрией стала бы менее проблематична.
Поэтому мы предположили, что частицы Стандартной модели удерживаются на одной бране, а частицы, ответственные за нарушение суперсимметрии, уединены на другой. Мы заметили, что в такой системе не обязательно возникают опасные взаимодействия, которые может индуцировать квантовая механика. Кроме эффектов нарушения суперсимметрии, которые могут передаваться через промежуточные частицы в балке, взаимодействия частиц Стандартной модели будут такими же, как и в теории с ненарушенной суперсимметрией. Таким образом, так же как в теории с точной суперсимметрией, нежелательные изменяющие аромат взаимодействия, несовместимые с экспериментами, не будут возникать. Частицы в балке, взаимодействующие с частицами как на нарушающей суперсимметрию бране, так и на бране Стандартной модели, будут точно определять, какие взаимодействия возможны, и среди них не будет с необходимостью запрещенных взаимодействий.
Конечно, некоторое нарушение суперсимметрии должно быть передано частицам Стандартной модели. В противном случае ничто не сможет увеличить массы суперпартнеров. Хотя мы не знаем точных значений масс суперпартнеров, экспериментальные ограничения совместно с ролью суперсимметрии в защите иерархии примерно указывают, каковы должны быть их массы.
Из экспериментальных ограничений можно получить качественные связи между массами суперпартнеров. Грубо говоря, все суперпартнеры имеют примерно одинаковые массы, и эти массы примерно равны масштабу массы слабых взаимодействий, равному 250 ГэВ. Нам нужно убедиться, что массы суперпартнеров попадают в этот интервал, но при этом нежелательные взаимодействия по-прежнему не возникают. Для того чтобы теория уединенного нарушения суперсимметрии имела шанс оказаться правильной, все должно складываться гармонично.
Ключом к успеху нашей модели было бы обнаружение промежуточной частицы, которая могла бы переносить данные о нарушении суперсимметрии к частицам Стандартной модели и придавать суперпартнерам нужные им массы.
Но мы хотели быть уверены, что наш переносчик не спровоцирует недопустимых взаимодействий.
Идеальным кандидатом выглядел гравитон. Эта частица живет в балке и взаимодействует с энергичными частицами, где бы они ни находились — на бране, нарушающей суперсимметрию, и на бране Стандартной модели. Кроме того, взаимодействия гравитона известны, они следуют из теории тяготения. Мы смогли показать, что взаимодействия гравитона, генерируя необходимые массы суперпартнеров, не приводят к взаимодействиям, перепутывающим кварки и лептоны, которые, как известно, отсутствуют в природе. Поэтому выбор гравитона выглядел многообещающе.
Когда мы рассчитывали массы суперпартнеров, которые получались в случае переносчика-гравитона, мы обнаружили, что несмотря на простоту составляющих, вычисления были на удивление тонкими. Классические вклады в нарушающие суперсимметрию массы оказались равными нулю, и нарушение суперсимметрии переносилось только квантово-механическими эффектами. Когда мы поняли это, мы назвали индуцированную гравитоном передачу нарушения суперсимметрии аномальной передачей. Мы выбрали такое название по аналогии с аномалиями, обсуждавшимися в гл. 14, так как специфические квантовомеханические эффекты нарушали симметрию, которая присутствовала бы в противном случае. Самое важное было в том, что поскольку массы суперпартнеров зависели от известных квантовых эффектов в Стандартной модели, а не от неизвестных взаимодействий в дополнительных измерениях, мы могли предсказать относительные величины масс суперпартнеров.
Потребовалось несколько дней на то, чтобы привести все это в порядок, поэтому в один и тот же день я могла переходить от разочарования к надежде. Я помню, как однажды за ужином удивила сидящих рядом, когда я совершенно обезумела от радости, так как заметила ошибку и решила задачу, не дававшую мне покоя весь день. В итоге Раман и я открыли, что если гравитация передает нарушение суперсимметрии, то уединенное нарушение суперсимметрии выполняется удивительно хорошо. Все суперпартнеры имеют правильные массы, а соотношение между массами калибрино и скварка лежит в желаемом интервале. Хотя не все работало так просто, как мы первоначально надеялись, важные соотношения между массами суперпартнеров вставали на место без введения невозможных взаимодействий, которые так досаждают другим нарушающим суперсимметрию теориям. При минимальных модификациях все работало.
И самое замечательное, что благодаря конкретным предсказаниям масс суперпартнеров нашу идею можно было проверять. Очень важным свойством уединенного нарушения суперсимметрии является то, что несмотря на чрезвычайно малые размеры дополнительных измерений, порядка 10-31 см, что всего лишь в сто раз превосходит крохотный планковский масштаб длины, существуют видимые следствия. Это противоречит стандартной идее, что только много большие измерения могут иметь видимые следствия, благодаря модифицированному закону тяготения или новым тяжелым частицам.
Хотя действительно верно, что мы не видели ни одного из экспериментальных следствий в условиях, когда дополнительные измерения малы, гравитон передает калибрино нарушение суперсимметрии весьма специфическим образом, что поддается точному подсчету, ибо известны гравитационные взаимодействия и другие взаимодействия, возникающие в теории с суперсимметрией. Модель уединенного нарушения суперсимметрии предсказывает определенные отношения масс для калибрино — партнеров калибровочных бозонов — и эти массы можно измерить.
Это очень обнадеживает. Если физики откроют суперпартнеров, они смогут затем определить, согласуются ли соотношения между их массами с тем, что мы предсказываем. Эксперимент по поиску этих калибровочных суперпартнеров находится в стадии подготовки на Тэватроне — протон-антипротонном коллайдере в лаборатории им. Э. Ферми, Иллинойс. Если нам повезет, мы узнаем результаты в течение ближайших нескольких лет[139].
В конце концов и Раман, и я были в разумной степени уверены, что нам удалось открыть что-то интересное. Но у каждого из нас оставалось беспокойство. Я немного боялась, что такую интересную идею, если она верна, не могли проглядеть, и что нам нужно еще убедиться, что мы не пропустили какой-то скрытой ошибки в нашей модели. Раман также думал, что идея слишком хороша, чтобы ее просметрели. Но он был уверен, что все правильно, и боялся только, что подобная идея в физической литературе уже была, а мы ее пропустили.
Он был недалек от истины. Аномальная передача нарушения суперсимметрии была независимо открыта примерно в то же время Джаном Джудиче из ЦЕРНа, Маркусом Люти из Мериленда, Хитоши Мураямой из Беркли и Рикардо Ратацци из Пизы, которые работали вместе тем же самым летом. Их статья вышла на следующий день после нашей. Их работа меня поразила. Я не могла понять, как две группы физиков одним и тем же летом проделали тот же самый извилистый путь сквозь идеи, но Раман правильно предположил, что у них могли быть похожие интересы. На самом деле мы оба были в определенном смысле правы. Хотя у другой группы были сходные идеи, их мотивация не была связана с дополнительными измерениями, а без них массы, порожденные аномальной передачей, были просто курьезом. Как Рикардо великодушно сказал физику Массимо Поррати, нашему общему другу, Раман и я сделали это лучше не потому, что наша версия аномальной передачи была более правильной, а потому, что у нас была причина, о которой любой бы заботился в первую очередь! Причиной были дополнительные измерения. Без них нарушение суперсимметрии не было бы уединено и массы, порожденные аномальной передачей, были бы затерты большими эффектами.
Другие физики также подключились потом к исследованию моделей уединенного нарушения суперсимметрии. Они нашли способы объединить этот подход с другими, более старыми идеями, чтобы построить еще более успешные модели, которые могли бы отражать реальный мир. Ученые даже нашли способы расширить идею уединения на четыре измерения.
Существует слишком много моделей, всех не перечислишь, поэтому позвольте отметить две идеи, которые я нахожу особенно интересными. Первая идея возникла из сотрудничества Рамана и Маркуса Люти. Они использовали идеи закрученной геометрии (описанной в гл. 20), чтобы заново переосмыслить следствия уединения в четырех измерениях. Руководствуясь этими идеями, они разработали новый класс четырехмерных моделей нарушения симметрии.
Другая интересная идея была названа калибровочной передачей. Идея состояла в том, чтобы передать нарушение суперсимметрии не через гравитон, а через калибрино, суперсимметричные партнеры калибровочных бозонов. Чтобы это работало, калибровочные бозоны и их партнеры не должны были быть зажаты на бране; они должны были иметь свободу передвижения по балку. Раман напомнил мне, что калибровочная передача была на самом деле одной из тех многих идей, которые мы ранее отбросили. Но блестящие моделестроители Дэвид Каплан, Грем Крибс и Мартин Шмальц, а также отдельно Захария Чако, Маркус Люти, Энн Нельсон и Эдуардо Понтон показали, что мы были слишком опрометчивы и что калибровочная передача может прекрасно работать при генерации нарушающих суперсимметрию масс, сохраняя при этом все преимущества уединенного нарушения суперсимметрии[140].
Уединение и сияющие массы
Уединенное нарушение симметрии — мощный инструмент для построения моделей. Реальный мир может содержать разделенные браны, и строя модели с учетом этого предположения, физики могут исследовать целый ряд возможностей.
В предыдущем разделе объяснялось, каким образом в теориях с суперсимметрией можно решить проблемы с меняющими аромат взаимодействиями. Но есть и другой вопрос, бросающий вызов строителю моделей в первую очередь — почему должны существовать разные ароматы кварков и лептонов с разными массами. Механизм Хиггса придает частицам их массы, но точные значения для каждого аромата различны. Это может быть правильным только в случае, когда каждый из ароматов взаимодействует по-разному с тем, что играет роль хиггсовской частицы. Поскольку три аромата каждого типа частиц, например кварки u, с и b, имеют в точности одинаковые калибровочные взаимодействия, возникает загадка, почему все они должны иметь разные массы. Чем-то они должны отличаться друг от друга, но физика частиц Стандартной модели не говорит нам, чем именно.
Мы можем пробовать строить модели, объясняющие разные массы. Но почти неизбежно любая модель будет также содержать нежелательные взаимодействия, которые будут менять ароматы. Нам требуется что-то, позволяющее безопасно различать ароматы, не порождая при этом проблемных взаимодействий.
Нима Аркани-Хамед и выходец из Германии физик Мартин Шмальц предположили, что различные частицы Стандартной модели живут на отдельных бранах, и это позволяет объяснить некоторые массы. Нима и Савас Димопулос обнаружили другую, еще более простую возможность. Они предположили, что существует брана, на которую были захвачены частицы Стандартной модели, и что взаимодействия между частицами на этой бране рассматривают все ароматы одинаково. Но при наличии только симметричных по ароматам взаимодействий, рассматривающих все ароматы одинаково, все частицы будут иметь точно одинаковые массы. Ясно, что мы можем объяснить разные массы только, если есть нечто, что воспринимает частицы по-разному.
Нима и Савас предположили, что другие частицы, ответственные за нарушение симметрии ароматов, были уединены на других бранах. Как и в случае уединенного нарушения суперсимметрии, нарушение симметрии ароматов может быть в этом случае связано с частицами Стандартной модели только через взаимодействия с частицами в балке. Если бы в балке существовало много частиц, взаимодействующих с частицами Стандартной модели, каждая из которых передавала бы нарушение симметрии ароматов от разных бран на разные расстояния, такая модель могла бы объяснить различие масс ароматов Стандартной модели. Нарушение симметрии, передаваемое от удаленных бран, индуцировало бы меньшие массы, чем нарушение симметрии, переданное от ближайших бран. Нима и Савас назвали свою идею сиянием, чтобы подчеркнуть этот факт. Так же, как свет кажется более тусклым, когда его источник находится дальше, эффект нарушения симметрии меньше, когда он порождается более далекой браной. В их сценарии различные ароматы кварков и лептонов будут различными, так как каждый из них будет взаимодействовать с разной браной на разном расстоянии.
Дополнительные измерения и уединение — новые захватывающие подходы к решению задачи в физике частиц. И не нужно на этом останавливаться. Недавно мы показали, что уединение может играть важную роль даже в космологии, науке об эволюции нашей Вселенной. Ясно, что нам еще предстоит открыть все достоинства вселенной (или мультивселенной), содержащей уединенные частицы, так что новые идеи еще придут.
Что нового
• Частицы могут быть уединены на разных бранах.
• Даже крохотные дополнительные измерения могут влиять на свойства наблюдаемых частиц.
• Уединенные частицы не обязательно подчиняются анархическому принципу. Не все взаимодействия обязательно происходят, так как удаленные частицы не могут взаимодействовать непосредственно.
• В модели, в которой частицы, участвующие в нарушении суперсимметрии, уединяются от частиц Стандартной модели, суперсимметрия может быть нарушена без введения взаимодействий, меняющих ароматы частиц.
• Уединенное нарушение суперсимметрии проверяемо на опыте. Если калибрино рождаются на коллайдерах большой энергии, мы можем сравнить массы калибрино и увидеть, согласуются ли их значения с предсказаниями.
• Уединенное нарушение симметрии ароматов может помочь объяснить различия в массах частиц.
Глава 18
Просачивающиеся пассажи: отпечатки дополнительных измерений
I was peeking
But it hasn’t been happened yet
I haven’t been given
My best souvenir I miss you
But I haven’t met you yet.
Bjork[141]
Афине пришлось признать, что она скучала по Икару. Даже несмотря на то что он часто ее раздражал, без него она чувствовала себя одинокой. Она с нетерпением ожидала приезда К. Квадрата, чей визит был запланирован в рамках студенческого обмена. Но ее соседи были напуганы предстоящим визитом, и Афину удивляла их ограниченность. Не имело значения, что он говорил на том же языке и вел себя так же, как все. к. Квадрат был чужестранцем, и в сложившейся обстановке этого было достаточно для того, чтобы переполошить соседей.
Когда Афина спросила соседей, почему они так испуганы, они ответили: «А что, если он пошлет за своими более тяжелыми родственниками? Что, если они не так хорошо воспитаны, как он, и придерживаются своих иностранных законов? и если они все сразу приедут, что случится тогда?»
К сожалению, Афина только подкрепила их опасения, сказав, что К. Квадрат и его родственники не могут в любом случае оставаться надолго, так как они все очень нестабильны, и семья К. Квадрата может совершать визиты только во время неразберихи на энергетических собраниях. Заметив, как неудачно она выразилась, Афина поспешила добавить, что во время их кратких и эмоциональных визитов иностранцы будут подчиняться местным законам. Афина убедила соседей и они все вместе вышли приветствовать клан К. Квадрата.
Ранее в этой книге я объясняла, каким образом могут быть спрятаны дополнительные измерения. Они могут быть свернуты или окружены бранами, так чтобы стать совсем незаметными. Но может ли вселенная с дополнительными измерениями действительно настолько полностью спрятать свою природу, чтобы ни одним своим свойством не выдать отличие от четырехмерного мира? В это трудно поверить. Даже если компактифицированные измерения так малы, что мы можем успокоить себя мыслью, что мир четырехмерен, мир с дополнительными измерениями должен содержать какие-то новые элементы, отличающие его от истинно четырехмерного мира.
Если дополнительные измерения существуют, они обязательно должны оставлять следы. Такими следами являются частицы, называемые частицами Калуцы — Клейна (частицами КК)[142]. Частицы КК — это дополнительные ингредиенты вселенной с дополнительными измерениями. Это четырехмерный отпечаток многомерного мира.
Если частицы КК существуют и достаточно легки, они могут рождаться на коллайдерах высоких энергий и оставлять свои следы в экспериментальных данных. Детективы многомерного мира — экспериментаторы — соберут вместе все отпечатки, преобразуя данные в судебное заключение о существовании мира дополнительных измерений. Эта глава посвящена частицам КК и вопросу о том, почему в мире с дополнительными измерениями вы можете быть уверены в их существовании.
Частицы Калуцы — Клейна
Даже если частицы перемещаются в пространстве дополнительных измерений, мы все же способны описать их свойства и взаимодействия в терминах четырехмерного мира. Ведь мы, в конце концов, не видим дополнительных измерений непосредственно, так что все должно проявляться так, как будто мир четырехмерен. Как жители Флатландии, которые видят только два пространственных измерения, могут наблюдать только двумерные диски, когда трехмерная сфера проходит по их миру, мы можем видеть только частицы, которые выглядят так, как будто они перемещаются в трех пространственных измерениях, даже если эти частицы берут начало в многомерном пространстве. Эти новые частицы, берущие начало в дополнительных измерениях, но кажущиеся нам дополнительными частицами в обычном четырехмерном пространстве-времени[143], и есть частицы Калуцы — Клейна.
Частицы Калуцы — Клейна есть проявление в четырех измерениях частицы из пространства с дополнительными измерениями. Аналогично тому, как любой звук, издаваемый скрипичной струной, можно представить как суперпозицию многих резонансных мод, поведение частицы из пространства с дополнительными измерениями можно воспроизвести, заменив ее подходящими частицами КК. Эти частицы полностью характеризуют многомерные частицы и геометрию многомерного пространства дополнительных измерений, в котором они перемещаются.
Чтобы воспроизвести поведение многомерных частиц, частицы КК должны нести экстра-импульс из дополнительных измерений. Каждая частица, которая перемещается в многомерном пространстве с дополнительными измерениями, может быть заменена в нашем эффективном четырехмерном описании частицами КК, имеющими правильные импульсы и взаимодействия, симулирующие рассматриваемую частицу из пространства с дополнительными измерениями. Вселенная с дополнительными измерениями принимает как знакомые частицы, так и их КК-родственников, имеющих экстрамерные импульсы в дополнительных измерениях, которые определяются детальными свойствами свернутого пространства.
Однако четырехмерное описание не содержит информации о положении или импульсе в дополнительных измерениях. Поэтому, когда мы рассматриваем экстра-мерный импульс частиц КК с точки зрения нашего четырехмерного пространства, его надо назвать как-то иначе. Связь между массой и импульсом, налагаемая специальной теорией относительности, показывает, что импульс в пространстве с дополнительными измерениями будет проявляться в четырехмерном мире как масса. Поэтому частицы КК похожи на известные нам обычные частицы, но с массами, отражающими наличие у них экстра-импульсов в дополнительных измерениях.
Массы частиц КК определяются геометрией пространства с дополнительными измерениями. Однако их заряды такие же, как у известных четырехмерных частиц. Это следует из того, что если известные частицы происходят из пространства с дополнительными измерениями, то и многомерные частицы должны нести те же заряды, что и известные частицы. Это верно и для частиц КК, симулирующих поведение многомерных частиц. Так, для каждой частицы должно быть много частиц КК с тем же зарядом, но разными массами. Например, если электрон перемещается в пространстве с дополнительными измерениями, у него будут КК-партнеры с тем же отрицательным зарядом. И если кварк перемещается в пространстве с дополнительными измерениями, у него появятся КК-родственники, которые, как и кварк, будут испытывать сильное взаимодействие. КК-партнеры имеют такие же заряды, как известные нам частицы, но массы КК-партнеров определяются дополнительными измерениями.
Определение масс частиц Калуцы — Клейна
Чтобы понять происхождение и массы частиц КК, требуется выйти за пределы интуитивной картины невидимых свернутых измерений, которую мы рассматривали ранее. Для простоты, рассмотрим сначала вселенную без бран, в которой каждая частица в основе многомерна и может перемещаться по всем направлениям, включая дополнительные. Рассмотрим конкретный пример пространства только с одним дополнительным измерением, свернутым в окружность, где элементарные частицы перемещаются внутри этого пространства. Если бы мы жили в мире, где правила бы классическая ньютоновская физика, частицы Калуцы— Клейна могли бы иметь любые значения импульса в дополнительных измерениях, и поэтому любые массы. Но так как мы живем в квантово-механической вселенной, дело обстоит иначе. Квантовая механика утверждает, что аналогично звукам скрипичных струн, в которые дают вклад только резонансные моды, только квантованные экстра-импульсы в дополнительных измерениях дают вклад, когда частицы КК воспроизводят движение и взаимодействия многомерной частицы. И точно так же, как звуки скрипичной струны зависят от ее длины, квантованные экстра-импульсы в дополнительных измерениях частиц КК зависят от размеров и формы этих дополнительных измерений.
Экстра-импульсы в дополнительных измерениях, которые несут частицы КК, проявляются в нашем четырехмерным мире как определенный набор масс частиц КК. Если физики обнаружат частицы КК, их массы расскажут нам о геометрии пространств с дополнительными измерениями. Например, если существует одно дополнительное измерение, свернутое в окружность, эти массы сообщат нам о размере дополнительного измерения.
Процедура поиска разрешенных импульсов (а следовательно, масс) для частиц КК во Вселенной со свернутым измерением очень похожа на метод, который используется для того, чтобы математически определить резонансные моды скрипки, а также на метод, использованный Бором для определения квантованных орбит электронов в атоме. Квантовая механика связывает все частицы с волнами, причем оказываются разрешенными только те волны, колебания которых укладываются целое число раз на окружности дополнительного измерения. Мы определяем разрешенные волны, а затем используем квантовую механику, чтобы связать длину волны с импульсом. Импульсы в дополнительных измерениях определяют разрешенные массы частиц КК, что мы и хотели узнать.
Всегда разрешена также постоянная волна — та, которая совсем не колеблется. Эта «волна» похожа на поверхность идеально спокойного пруда, без видимой ряби, или на скрипичную струну, которую еще не дернули. Такая волна вероятности имеет одно и то же значение везде в дополнительных измерениях. Из-за постоянного значения этой плоской волны вероятности связанная с ней частица КК не отдает предпочтения никакому конкретному положению в пространстве дополнительных измерений. Согласно квантовой механике, эта частица не несет никакого импульса в пространстве дополнительных измерений и, согласно специальной теории относительности, не имеет дополнительной массы.
Таким образом, легчайшая частица КК — это та, которая связана с постоянным значением вероятности в дополнительном измерении. При низких энергиях это единственная частица КК, которая может родиться. Так как у нее нет ни импульса, ни структуры в дополнительном измерении, она неотличима от обычной четырехмерной частицы с теми же массой и зарядом. Имея низкую энергию, частица из пространства с дополнительными измерениями не способна навиваться на компактное свернутое измерение. Иными словами, при низких энергиях невозможно произвести ни одной из дополнительных частиц КК, которые отличают нашу Вселенную от вселенной с большим числом измерений. Низкоэнергетические процессы и легчайшие частицы КК ничего не сообщат нам о существовании дополнительных измерений, независимо от их размеров или формы.
Однако, если вселенная содержит дополнительные измерения, и ускорители частиц достигнут достаточно больших энергий, они смогут создать более тяжелые частицы КК. Эти более тяжелые частицы КК, переносящие ненулевой импульс в дополнительных измерениях, станут первым реальным свидетельством дополнительных измерений. В нашем примере более тяжелые частицы КК связаны с волнами, обладающими структурой вдоль свернутого в окружность дополнительного измерения; волны колеблются, накручиваясь вокруг свернутого измерения и совершая колебания вверх и вниз целое число раз.
Легчайшей из таких частиц КК будет та, у которой функция вероятности имеет наибольшую длину волны. А наибольшая длина волны, для которой колебания укладываются вдоль окружности, будет у той волны, которая колеблется вверх и вниз ровно один раз, пока волна накручивается на свернутое измерение. Такая длина волны определяется размером окружности в дополнительном измерении. Большие длины волны не уместятся, волна будет рассогласована, вернувшись в ту же точку на окружности. Частица с такой волной вероятности есть легчайшая частица КК, которая «помнит» свое происхождение от дополнительных размерностей.
Разумно считать, что длина волны, связанной с этой легчайшей частицей с ненулевым импульсом в дополнительном измерении, будет порядка размера дополнительного измерения. В конце концов, интуиция подсказывает нам, что только нечто достаточно малое, чтобы исследовать свойства или взаимодействия на крохотном масштабе, будет чувствительно к существованию свернутого измерения. Пытаться исследовать дополнительное измерение с большей длиной волны похоже на попытку измерить положение атома с помощью рулетки. Например, если вы пытаетесь детектировать дополнительное измерение с помощью света или другого пробного тела определенной длины волны, то свет должен иметь длину волны, меньшую, чем размер дополнительного измерения. Так как квантовая механика сопоставляет волны вероятности частицам, то утверждения о длинах волн пробных тел переводятся в утверждения о свойствах частиц. Только частицы достаточно малой длины волны и поэтому (в силу соотношения неопределенностей) с достаточно большим импульсом в дополнительном измерении и массой могут быть чувствительны к существованию дополнительных измерений.
Другая привлекательная черта легчайших частиц КК с ненулевым импульсом в дополнительных измерениях заключается в том, что ее импульс (а следовательно, и масса) становится меньше, когда дополнительное измерение становится больше. Большее дополнительное измерение должно быть более доступно и должно приводить к большему числу непосредственно наблюдаемых следствий, так как легкие частицы проще рождать и обнаруживать.
Если дополнительные измерения действительно существуют, то легчайшая частица КК не станет единственным свидетельством их существования. Другие частицы с большим импульсом могут оставить еще более заметные следы дополнительных измерений на коллайдерах частиц. Волна вероятности у этих частиц такова, что она колеблется более одного раза, перемещаясь вдоль свернутого измерения. Так как п-я такая частица будет соответствовать волне, колеблющейся п раз, пока она навивается на свернутое измерение, массы этих частиц КК будут все целыми кратными легчайшей массы. Чем больше импульсы, тем отчетливее следы дополнительных измерений, которые может оставить на коллайдерах частица КК. На рис. 74 схематически показаны значения масс частиц КК, пропорциональные обратному размеру дополнительного измерения, и пара волн, соответствующих этим массивным частицам.
Большое количество последовательно утяжеляющихся частиц КК можно сравнить с поколениями семьи иммигрантов. Члены самого юного поколения, родившиеся в США, полностью ассимилировались в американскую культуру, идеально разговаривают по-английски и вообще не выдают своего иностранного происхождения. Для предыдущего поколения, их родителей, все не совсем так: они, вероятно, говорят с чуть заметным акцентом, и по случаю могут вставить несколько пословиц родной страны. Старшее поколение говорит все больше по-иностранному, носит одежду и рассказывает истории из их родной страны. Можно сказать, что старшие поколения добавляют культурные измерения к тому, что в противном случае было бы менее ярким, однородным обществом.

Аналогично, легчайшие частицы КК неотличимы от частиц в фундаментально четырехмерном мире; только более массивные «старые связи» будут обнаруживать свидетельства дополнительных измерений. Хотя легчайшие из частиц КК будут казаться четырехмерными, их происхождение станет ясным, как только будет произведено достаточное количество энергии, чтобы родить более массивных «стариков».
Если экспериментаторы обнаружат новые тяжелые частицы с теми же зарядами, как и у привычных нам частиц, и похожими друг на друга массами, эти частицы будут сильным свидетельством в пользу дополнительных измерений. Если такие частицы имеют одинаковые заряды и возникают с регулярными интервалами по массе, это будет, весьма вероятно, означать, что открыто простое свернутое измерение.
Однако более сложная геометрия дополнительных измерений будет приводить к более сложной структуре масс. Если будет открыто достаточное количество таких частиц, то частицы КК откроют нам не только существование дополнительных измерений, но и их размеры и форму. Какой бы ни была геометрия скрытых измерений, массы частиц КК будут от нее зависеть. Во всех случаях частицы КК и их массы могут многое рассказать нам о свойствах дополнительных измерений.
Экспериментальные ограничения
До недавнего времени большинство теоретиков-струнников предполагало, что дополнительные измерения имеют размеры не больше крохотного планковского масштаба длины. Так было потому, что гравитация становится сильной на планковском масштабе энергий, а теория квантовой гравитации, которой могла бы быть теория струн, должна вступать в игру в этом месте. Но планковский масштаб длины много меньше любой длины, которую мы можем изучать экспериментально. Крохотный планковский масштаб длины соответствует (согласно квантовой механике и специальной теории относительности) колоссальному планковскому масштабу масс (или энергий), в десять тысяч триллионов раз больше того, что могут достичь современные ускорители частиц. Частицы КК планковской массы были бы настолько тяжелыми, что оказались бы далеко за пределами любого доступного эксперимента.
Однако возможно, что размер дополнительных измерений больше, а частицы КК легче. Поэтому почему бы не спросить, что экспериментальные тесты говорят нам о размерах дополнительных измерений? Что мы на самом деле знаем, если отбросить приемные теоретические представления?
Если мир имеет дополнительные измерения, и в нем нет бран, тогда все знакомые частицы, например электрон, будут иметь своих КК-партнеров. Это будут частицы, имеющие в точности тот же заряд, что и знакомые нам частицы, но обладающие импульсом в дополнительных измерениях. КК-партнеры электрона будут отрицательно заряжены, как электрон, но тяжелее. Если дополнительное измерение свернуто в окружность, масса легчайшей из таких частиц будет отличаться от массы электрона на величину, обратно пропорциональную размеру дополнительного измерения. Это означает, что чем больше дополнительное измерение, тем меньше масса частицы. Так как большие измерения порождают более легкие частицы КК, ни одну из которых не наблюдали экспериментально, ограничения на массы частиц КК приводят к ограничениям на разрешенный размер дополнительного свернутого измерения.
До сих пор не было никаких признаков рождения таких заряженных частиц на коллайдерах, работающих при энергиях вплоть до 1000 ГэВ. Так как частицы КК были бы характерным признаком дополнительных измерений, тот факт, что мы их не видим, говорит нам, что дополнительные измерения не могут быть слишком большими. Современные экспериментальные ограничения утверждают, что дополнительные измерения не могут быть больше[144], чем 10-17 см. Это очень мало, намного меньше, чем все, что мы способны видеть непосредственно.
Этот предел на размер дополнительного измерения примерно в десять раз меньше, чем масштаб длины слабых взаимодействий. Однако, даже несмотря на то, что 10-17 см — это мало, все равно это огромное число по сравнению с планковским масштабом длины 10-33 см, что на шестнадцать порядков меньше. Это означает, что дополнительные размерности могут быть намного больше, чем планковский масштаб длины, и при этом ускользать от обнаружения. Греческий (современный) физик Игнаций Антониадис был одним из первых, кто представил, что дополнительные измерения имеют не планковский размер, а вместо этого сравнимы по размеру с масштабом длины, связанным со слабым взаимодействием. Он размышлял о том, какая новая физика может возникнуть, когда коллайдеры хоть немного увеличат свою энергию. В конце концов, проблема иерархии говорит нам, что мы должны что-то увидеть при тех энергиях, при которых будут рождаться частицы с энергиями и массами порядка масштаба слабых взаимодействий.
Но даже приведенный выше предел на размер дополнительных измерений не обязательно всегда применим. Частицы КК являются следами дополнительных измерений, но они могут быть хитрыми и удивительно трудными для поиска. Недавно мы узнали чуть больше о частицах КК и о том, как они могут выглядеть. В следующих главах мы объясним новейшие идеи о том, почему, добавив в игру браны, дополнительные измерения могут стать больше 10-17 см и все же ускользать от обнаружения, вопреки ожиданиями, что большие измерения порождают более легкие частицы КК. Некоторые модели с поразительно большими измерениями — так что вы вправе думать, что они приведут к хорошо видимым следствиям — могут быть невидимыми, помогая, тем не менее, объяснить непонятные свойства частиц Стандартной модели. В гл. 22 мы опишем еще более удивительный результат: бесконечно большое дополнительное измерение может порождать бесконечно много легких частиц КК, не оставляя при этом никаких наблюдаемых следов.
Что нового
• Моды Калуцы — Клейна (КК) — это частицы, имеющие экстра-импульс в дополнительных измерениях; они являются многомерными лазутчиками в нашем четырехмерном мире.
• Частицы КК выглядят как тяжелые частицы с теми же зарядами, что и у известных частиц.
• Массы и взаимодействия частиц КК определяются теорией с дополнительными измерениями; поэтому они отражают свойства пространства-времени с дополнительными измерениями.
• Если бы мы могли найти и измерить свойства всех частиц КК, мы бы знали размеры и форму дополнительных измерений.
• Современные экспериментальные ограничения говорят нам, что если все частицы перемещаются по пространству с дополнительными измерениями, размер этих измерений не может превышать 10-17 см.
Глава 19
Объемные пассажи: большие дополнительные измерения
I couldn’t even see the millimeter when it fell.
Eminem[145]
После краткого визита К. Квадрата Афина провела много времени в местном Интернет-кафе. Она была в приподнятом настроении из-за своего недавнего открытия ряда загадочных новых веб-сайтов, самым интригующим из которых был сайт xxx.sodoseandyetsofar.al. Афина подозревала, что эти сайты с наводящим названием были следствием недавнего слияния мультимедийных фирм «Америка на Бране» и «Пространство-время Уорнера», но ей пришлось уйти, прежде чем она могла заняться исследованием.
Когда Афина пришла домой, она бросилась к компьютеру, и снова стала искать экзотические гиперссылки, которые были так легко доступны из Интернет-кафе. Однако, к ее разочарованию. Киберняня не допустила ее ко входу на запрещенные размерно расширенные сайты[146]. Однако, замаскировавшись под надежным псевдонимом Ментор, Афина победила киберцензора и сумела вернуться к загадочной гиперссылке.
Афина втайне надеялась, что К. Квадрат передал ей послание, которое было спрятано на вебстранице, но понять сайты было нелегко, и ей удалось узреть только несколько потенциально осмысленных сигналов. Она решилась получше изучить их содержание и надеялась, что слияние, не в пример другому слиянию с похожим именем, продлится достаточно долго, чтобы она успела в них разобраться.
На Оксфордской конференции по суперсимметрии 1998 года физик из Станфорда Савас Димопулос сделал один из самых интересных докладов. Он доложил работу, выполненную им в сотрудничестве с двумя другими физиками, Нимой Аркани-Хамедом и Гием Двали. Колоритные имена этих трех физиков соответствовали их колоритным характерам и идеям. Савас всегда очень возбужден своими проектами; его сотрудники говорят мне, что его энтузиазм всегда очень заразителен. Он был так захвачен дополнительными измерениями, что сказал своему коллеге, что все новые неисследованные физические идеи заставляют его чувствовать себя ребенком в кондитерском магазине — он хочет съесть все, прежде чем кто-то другой получит хоть что-нибудь. Гия, физик из бывшей Советской Грузии, любит рисковать, как в своем подходе к физике, так и при безрассудном поведении во время занятий альпинизмом. Однажды он без всяких припасов застрял в непогоду на две ночи на вершине горы на Кавказе. Нима, физик из иранской семьи, очень энергичен, стимулирует дискуссии и живо излагает свои мысли. В настоящее время он мой коллега в Гарварде. Его можно часто видеть в коридоре, где он с энтузиазмом объясняет свои последние исследования и предлагает присоединиться к работе.
По иронии судьбы, доклад Саваса на конференции по суперсимметрии, который был посвящен совсем не суперсимметрии, а дополнительным измерениям, отнял у него часть лавров. Савас объяснил, что не суперсимметрия, а дополнительные измерения могут быть физической теорией, лежащей в основе Стандартной модели. Если его предложение было верным, то, когда экспериментаторы начнут изучать в ближайшем будущем слабую шкалу, они могух ожидать найти не свидетельства суперсимметрии, а свидетельства дополнительных измерений.
В этой главе представлена идея Аркани-Хамеда, Димополуса и Двали[147] о том, как очень большие измерения могут объяснить слабость гравитации. По существу, большие дополнительные измерения могут растворить гравитационное взаимодействие настолько сильно, что интенсивность гравитации станет намного слабее, чем показывают оценки без дополнительных измерений. Их модели на самом деле не решили проблемы иерархии, так как еще нужно объяснить, почему измерения столь велики. Но АДД надеялись, что этот новый вопрос будет более податлив.
Мы рассмотрим также связанный вопрос, заданный АДД. насколько большими могут быть свернутые дополнительные измерения, если частицы Стандартной модели захвачены браной и не могут свободно перемещаться по балку, так чтобы не войти в противоречие с экспериментальными результатами? Найденный ими ответ был поразительным. К моменту, когда они писали свою статью, дело выглядело так, будто дополнительные измерения могли иметь размеры порядка миллиметра.
Измерения, размером (почти) в миллиметр
В модели АДД, как и в модели уединения, которую я описывала в гл. 17, частицы Стандартной модели захвачены на брану. Однако две модели имеют весьма различающиеся цели, так что остальные свойства совершенно различны. В то время как модель уединения имела одно дополнительное измерение, простирающееся между бранами, все модели АДД имели более одного измерения, причем эти измерения были свернуты. В зависимости от деталей реализации, пространство в этих моделях содержало два, три или более дополнительных свернутых измерений. Кроме того, модель АДД содержит единственную брану, на которую захвачены частицы Стандартной модели, но эта брана не ограничивает пространство. Она просто сидит внутри дополнительных свернутых измерений, как показано на рис. 75.
Вопрос, на который АДД хотели ответ найти согласно своей схеме, заключался в том, каким образом большие дополнительные измерения могут оставаться скрытыми, если все частицы Стандартной модели захвачены на брану, а единственным взаимодействием в многомерном балке является гравитация. Найденный ими ответ удивил большинство физиков. В противоположность размеру в одну сотую от одной тысячной от одной триллионной доли сантиметра, который мы рассматривали в предыдущей главе, эти дополнительные свернутые измерения могут быть размером в миллиметр. (На самом деле несколько неправильно приводить сейчас точное число, потому что, как мы обсудим ниже в этой главе, физики в Университете Вашингтона с тех пор экспериментально искали дополнительные измерения размером с миллиметр, но не нашли их. На основании их результатов мы теперь знаем, что дополнительные измерения должны быть меньше одной десятой миллиметра, или они должны быть исключены. Тем не менее существование измерений размером даже в одну десятую миллиметра все равно было бы достаточно поразительным.)

Вы можете подумать, что если бы измерения были величиной с миллиметр (или даже в десять раз меньше), мы бы о них уже знали. В конце концов, каждый, кто не видит предмет размером с миллиметр, нуждается в новых очках. По масштабам физики частиц миллиметр — огромная величина.
Чтобы дать вам представление о том, насколько экстраординарными были бы дополнительные измерения размером в миллиметр, или даже в одну десятую долю миллиметра, перечислим типы масштабов длины, которые мы до сих пор обсуждали. Планковский масштаб длины находится вне пределов любого экспериментального поиска и равен 10-33 см. ТэВный масштаб, который сейчас исследуют в экспериментах, порядка 10-17 см; физики проверили электромагнитное взаимодействие вплоть до масштабов порядка 10-17 см. Те размеры, о которых говорили АДД, чудовищно велики по сравнению с этими. При отсутствии бран, дополнительные измерения размером в миллиметр были бы абсурдом, который должен быть отброшен.
Однако браны делают потенциально возможными намного большие дополнительные измерения. Браны могут захватывать кварки, лептоны и калибровочные бозоны, так что только гравитация чувствует полное число дополнительных измерений пространства. В сценарии АДД, предполагающем, что все, кроме гравитации, захвачено на брану, все, что не включает гравитацию, должно выглядеть точно так же, как если бы не было никаких дополнительных измерений, даже если бы дополнительные измерения были необычайно велики.
Например, все, что вы видите, будет выглядеть четырехмерно. Ваш глаз детектирует фотоны, а фотоны в модели АДД захвачены на брану. Поэтому объекты, которые вы видите, будут выглядеть так, как будто существует только три пространственных измерения. Если фотоны захвачены на брану, то неважно, насколько сильны стекла ваших очков, — вы никогда непосредственно не увидите никаких свидетельств дополнительных измерений.
На самом деле, увидеть свидетельства существования измерений миллиметровых размеров в сценарии АДД можно только с помощью необычайно чувствительного гравитационного пробного тела. Все обычные процессы физики частиц, например взаимодействия, передаваемые электромагнитными силами, рождение электрон-позитронных пар и связь нуклонов за счет сильного взаимодействия, возникают только на четырехмерной бране, и будут в точности такими же, как в чисто четырехмерной вселенной.
Заряженные частицы КК также не составляют проблемы. В предыдущей главе объяснялось, что дополнительные измерения не могут быть очень большими, когда все частицы находятся в балке, так как, если бы они там были, мы бы уже видели КК-партнеров частиц Стандартной модели. Но в сценарии АДД это не так, потому что все частицы Стандартной модели, например электрон, захвачены на брану. Таким образом, частицы Стандартной модели, которые не перемещаются в балке с дополнительным числом измерений, не будут нести связанного с дополнительными измерениями импульса. Частицы Стандартной модели, захваченные на брану, не будут поэтому иметь КК-партнеров. А так как нет КК-партнеров, ограничения, основанные на частицах КК, вроде рассмотренных в последней главе, станут неприменимыми.
На самом деле в модели АДД единственная частица, у которой обязаны быть КК-партнеры, это гравитон, который, как мы знаем, должен перемещаться в балке с дополнительным числом измерений. Однако КК-партнеры гравитона взаимодействуют намного слабее, чем КК-партнеры Стандартной модели. В то время как КК-партнеры Стандартной модели взаимодействуют через электромагнетизм, слабое взаимодействие и сильное взаимодействие, КК-партнеры гравитона взаимодействуют только через гравитационное поле, так же слабо, как сам гравитон. КК-партнеров гравитона будет намного сложнее рождать и детектировать, чем КК-партнеров частиц Стандартной модели. Кстати, никто еще никогда непосредственно не видел гравитон. Его КК-партнеров, взаимодействующих столь же слабо, как сам гравитон, будет найти не легче.
АДД понимали, что если единственные ограничения на дополнительные измерения идут от гравитации, размер дополнительного измерения в их сценарии, где частицы Стандартной модели удерживаются на бране, может быть много больше, чем предлагалось в предыдущей главе. Причина в том, что гравитация очень слаба, и ее поэтому необычайно трудно исследовать экспериментально. Для легких объектов на близких расстояниях гравитация так слаба, что ее эффекты полностью перекрываются другими взаимодействиями.
Например, гравитационная сила между двумя электронами в 1043 раз слабее электромагнитной силы. Гравитационное притяжение Земли доминирует только потому, что полный заряд Земли равен нулю. На малых масштабах играет роль не только полный заряд, но и то, как распределены заряды. Чтобы проверить закон тяготения между малыми телами, гравитационное притяжение должно быть экранировано даже от мельчайшего влияния других взаимодействий. Хотя планеты вращаются вокруг Солнца, Луна вращается вокруг Земли и эволюция самой вселенной говорит нам о форме закона тяготения на очень больших расстояниях, закон тяготения очень трудно проверить на малых расстояниях. Мы знаем о гравитации намного меньше, чем о других взаимодействиях. Таким образом, если гравитация — единственное взаимодействие в балке, существование удивительно больших дополнительных измерений не будет противоречить ни одному экспериментальному результату. Дополнительные измерения с находящимися на бранах частицами трудно наблюдать.
В 1996 году, когда АДД писали свою работу, ньютоновский закон обратных квадратов был проверен только до расстояний порядка миллиметра. Это означало, что дополнительные измерения могут быть размером с миллиметр, и никто еще не видел ни одного их проявления. Как писали АДД в своей работе: «Наша интерпретация MPl [планковской энергии] как фундаментального энергетического масштаба [где гравитационные взаимодействия становятся сильными] основана, таким образом, на предположении, что гравитация остается немодифицированной в интервале 33 порядков величины между точкой, где она измерена… вплоть до планковской длины 10-33 см»[148]. Иными словами, в 1998 году ничего не было известно о гравитации из экспериментов на расстояниях меньше миллиметра. На меньших расстояниях закон, которому подчиняется гравитационная сила, может быть совсем другим, например, гравитационное притяжение может увеличиваться намного быстрее при сближении тел друг с другом, но никто пока этого не знает.
Большие измерения и проблема иерархии
Возможность существования больших дополнительных измерений было важной идеей. Но АДД не занимались изучением больших дополнительных измерений просто для того, чтобы исследовать абстрактные возможности. Их истинным интересом была физика частиц, в частности проблема иерархии.
Как объяснялось в гл. 12, проблема иерархии заключается в большом отношении масштаба массы слабых взаимодействий и планковского масштаба масс, т. е. тех масс, которые мы ассоциируем с физикой частиц и гравитацией. До недавнего времени главный вопрос, который задавали себе физики-частичники, заключался в том, почему масштаб массы слабых взаимодействий так мал, несмотря на большие (порядка планковского масштаба масс) [149] виртуальные вклады в массу хиггсовской частицы, которые стремятся сделать ее больше. Пока физики не начали размышлять о дополнительных измерениях, все попытки исследовать проблему иерархий сводились к расширению Стандартной модели в надежде найти более полную фундаментальную теорию физики частиц, которая бы объяснила, почему масштаб массы слабых взаимодействий настолько меньше планковского масштаба.
Но проблема иерархии заключается в огромной несоразмерности двух чисел. Загадка в том, почему планковская шкала и слабая шкала столь различны. Проблема иерархии может быть перефразирована другим способом: почему планковский масштаб масс так велик, в то время как масштаб массы слабых взаимодействий так мал, или, эквивалентно, почему настолько мала интенсивность гравитационного взаимодействия, действующего на элементарные частицы? С этой точки зрения из проблемы иерархии вытекает вопрос о том, не является ли гравитация, а не физика частиц, чем-то отличным от того, что предполагали физики.
АДД рассмотрели эту логическую цепочку и показали, что попытки решить проблему иерархии путем расширений Стандартной модели идут по неверному пути. Они заметили, что достаточно большие дополнительные измерения могут столь же хорошо решить проблему. Они предположили, что фундаментальный масштаб масс, определяющий интенсивность гравитации, — это не планковский масштаб масс, а значительно меньший масштаб масс порядка ТэВ.
Однако АДД столкнулись с вопросом, почему гравитация должна быть столь слаба. В конце концов причина, по которой планковский масштаб масс настолько велик, заключается в слабости гравитации — интенсивность гравитационного взаимодействия обратно пропорциональна этому масштабу. Много меньший фундаментальный масштаб масс для гравитации сделал бы гравитационные взаимодействия намного более сильными.
Но эта проблема не была непреодолимой. АДД заметили, что только гравитация в дополнительных измерениях была бы по необходимости сильной. Они показали, что большие дополнительные измерения могут настолько ослабить интенсивность гравитации, что несмотря на очень большую величину гравитационного взаимодействия в дополнительных измерениях, гравитация в эффективной теории с меньшим числом измерений будет очень слабой. В их картине гравитация кажется нам слабой, так как ослабляется, растворяясь в очень большом пространстве с дополнительными измерениями. С другой стороны, электромагнитное, сильное и слабое взаимодействия не будут малыми, так как они будут захвачены браной и вообще не будут ослабляться. Таким образом, большие измерения и брана могут разумно объяснить, почему гравитация настолько слабее всех других взаимодействий.
Нима говорил мне, что поворотной точкой в их исследовании был момент, когда он и его соавторы поняли точную связь между интенсивностями гравитации в пространствах с большим и малым числом измерений. Эта связь не была новой. Например, теоретики-струнники всегда использовали ее для того, чтобы связать четырехмерный масштаб гравитации с десятимерным. Как я коротко объясняла в гл. 16, Хоржава и Виттен использовали связи между интенсивностями десяти- и одиннадцатимерной гравитации, когда они заметили, что гравитацию можно объединить с другими взаимодействиями: большое одиннадцатое измерение позволяет гравитационному масштабу в пространстве с дополнительными измерениями, а следовательно, масштабу струны иметь величину порядка масштаба ТВО. Но никто до этого не обращал внимания на то, что гравитация в пространстве с дополнительными измерениями может быть достаточно сильна, чтобы решить проблему иерархии, если дополнительные измерения достаточно большие, чтобы нужным образом ее ослабить. После того как Нима, Савас и Гия немного подумали о дополнительных измерениях и поняли, как связать гравитацию в пространствах с малым и большим числом измерений, они вывели это экстраординарное следствие.
Связь между гравитацией в пространствах с большим и малым числом измерений
В гл. 2 мы видели, что если рассматривать только те расстояния, которые больше размера свернутых дополнительных измерений, дополнительные измерения остаются неощутимыми. Однако это не обязательно означает, что дополнительные измерения не приводят к физическим следствиям; даже несмотря на то, что мы их не видим, эти измерения могут оказывать влияние на значения тех величин, которые мы наблюдаем. Пример этого явления приведен в гл. 17. В модели уединенного нарушения суперсимметрии (где нарушение суперсимметрии происходило на удаленной бране, а гравитон переносил нарушение к супер-симметричным партнерам частиц Стандартной модели) массы суперпартнеров говорили о том, что нарушение суперсимметрии связанно с дополнительными измерениями и передается через гравитацию.
Мы сейчас рассмотрим другой пример, в котором дополнительные измерения влияют на значения измеряемых величин. Размеры компактифицированных измерений определяют связь между интенсивностью четырехмерной гравитации (той, которую мы наблюдаем) и интенсивностью гравитации в исходном пространстве с дополнительными измерениями. Гравитация ослабляется в дополнительных измерениях, когда свернутые дополнительные измерения охватывают больший объем.
Чтобы понять, как это происходит, вернемся к примеру в гл. 2, где мы рассматривали трехмерную вселенную садового шланга как аналогию для трехмерного пространства балка, ограниченного бранами. Если вода поступает в шланг через небольшой прокол (рис. 23 на стр. 53), сначала она будет бить струей, а затем растечется по всем трем измерениям. Однако, как только вода заполнит весь шланг, она будет течь только вдоль шланга — в этом причина того, что шланг кажется одномерным, когда мы проверяем закон тяготения на расстояниях, больших размера дополнительных измерений.
Но даже несмотря на то что вода течет только вдоль единственного измерения шланга, ее давление зависит от размера сечения шланга. Чтобы это понять, представим, что ширина шланга увеличивается. Тогда вода, вошедшая через прокол, будет растекаться по большей области, и давление воды в шланге станет меньше.
Если давление воды представляет силовые линии гравитационного поля, а сама вода, попадающая в шланг через прокол, представляет линии поля, исходящие от массивного тела, то силовые линии массивного тела первоначально будут расходиться по всем трем направлениям, как вода в предыдущем примере. Когда силовые линии достигнут стенок вселенной (браны), они искривятся и будут распространяться только вдоль одного большого измерения. В случае шланга мы обнаружили, что чем шире насадка, тем слабее давление воды. Аналогично, площадь дополнительных измерений в нашей игрушечной вселенной садового шланга будет определять, насколько разбавятся силовые линии в мире с меньшим числом дополнительных измерений. Чем больше площадь дополнительных измерений, тем слабее будет интенсивность гравитационного поля в эффективной вселенной в пространстве с меньшим числом измерений.
Аналогичные рассуждения применимы к свернутым измерениям во вселенной с любым числом свернутых измерений. Чем больше объем дополнительных измерений, тем больше ослаблено гравитационное взаимодействие и тем меньше интенсивность гравитации. Мы можем увидеть это на примере шланга с дополнительным числом измерений, аналогичного уже рассмотренному. Гравитационные силовые линии в шланге с дополнительными измерениями сначала будут распространяться по всем измерениям, включая дополнительные свернутые измерения. Силовые линии достигнут границы свернутых измерений, после чего они будут распространяться только вдоль бесконечных измерений пространства с меньшим числом измерений. Первоначальное растекание в дополнительных измерениях уменьшит плотность силовых линий в пространстве с меньшим числом измерений, так что интенсивность наблюдаемой здесь гравитации будет меньше.
Снова о проблеме иерархии
Из-за ослабления гравитации в дополнительных измерениях, гравитация в пространстве с меньшим числом измерений становится слабее, когда объем компактифицированного пространства дополнительных измерений растет. АДД заметили, что это ослабление гравитации в дополнительных измерениях в принципе может быть настолько большим, что оно может объяснить наблюдаемую слабость четырехмерной гравитации в нашем мире.
Они рассуждали так. Предположим, что гравитация в теории с дополнительными измерениями зависит не от колоссального планковского масштаба масс 1019 ГэВ, а от много меньшей энергии порядка 1 ТэВ, что на шестнадцать порядков меньше. Они выбрали ТэВ для избавления от проблемы иерархии: если ТэВ или какая-то энергия вблизи этого значения равна той энергии, при которой гравитация становится сильной, в физике частиц не будет иерархии масс. Все, включая физику частиц и гравитацию, будет характеризоваться общим масштабом порядка ТэВ. Таким образом, в их модели будет нетрудно получить разумно легкую хиггсовскую частицу массой порядка ТэВ.
Согласно их предположению, при энергиях порядка ТэВ гравитация в пространстве с дополнительными измерениями будет довольно сильным взаимодействием, сравнимым по интенсивности с другими известными взаимодействиями. Поэтому, чтобы получить осмысленную теорию, согласующуюся с тем, что мы наблюдаем, АДД потребовалось объяснить, почему четырехмерная гравитация выглядит настолько слабой. Дополнительным предположением в их модели была идея, что дополнительные измерения необычайно велики. И в конце концов нам бы хотелось объяснить этот большой размер. Но, согласно предположению АДД, свернутые измерения охватывают такой большой объем. И если следовать логике предыдущего раздела, четырехмерная гравитация будет чрезвычайно слабой. Гравитация в нашем мире будет слабой, потому что дополнительные измерения велики, а не потому, что существует фундаментальная большая масса, ответственная за крохотное гравитационное взаимодействие. Планковский масштаб масс, который мы измеряем в четырех измерениях, велик (из-за чего гравитация кажется слабой) только потому, что гравитация растворилась в больших дополнительных измерениях.
Насколько большими должны быть эти дополнительные измерения? Ответ зависит от числа дополнительных измерений. АДД рассматривали в своих моделях разные возможности для числа измерений, поскольку эксперименты еще не выявили, сколько существует измерений. Заметим, что нас сейчас интересуют только большие измерения. Таким образом, если вам кажется, что вы знаете, что число пространственных измерений равно девяти или десяти, вы можете рассматривать разные возможности для числа больших измерений, и предполагать, что все другие измерения достаточно малы и могут быть проигнорированы.
Размер измерений в схеме АДД зависит от того, насколько их много, так как объем зависит от количества измерений. Если все измерения одного размера, область с большим числом измерений будет охватывать больший объем, чем область с меньшим числом измерений, и будет поэтому больше ослаблять гравитацию. Это легко видно из того, что тела с меньшим числом измерений содержатся внутри тел с большим числом измерений. Если вернуться к аналогии с разбрызгивателем в гл. 2, то видно, что цветок получает больше воды, если вода разбрызгивается только вдоль некоторого отрезка (одно измерение), чем от разбрызгивателя, который подает воду на площадь, ограниченную окружностью (два измерения) с диаметром того же размера. Когда вода разбрызгивается по области с большим числом измерений, в каждое место области попадает меньше воды.
Если бы было только одно большое дополнительное измерение, его размер должен был быть огромным, чтобы удовлетворить предложению АДД. Чтобы в достаточной степени ослабить гравитацию, его размер должен был быть порядка расстояния от Земли до Солнца. Это недопустимо. Если бы дополнительное измерение было таким большим, вселенная вела бы себя так, как будто она пятимерная на измеряемых расстояниях. Мы уже знаем, что ньютоновский закон для силы тяготения применим на этих расстояниях; большое дополнительное измерение, которое изменяло бы гравитацию на столь больших расстояниях, безусловно исключено.
Однако всего лишь с двумя дополнительными измерениями размер измерений становится приемлемо мал. Если бы существовало ровно два дополнительных измерения, они могли бы быть размером с миллиметр, и при этом адекватно ослаблять гравитацию. В этом причина того, что АДД уделили так много внимания миллиметровому масштабу. Этот масштаб не только находился на пороге экспериментальных тестов, но два дополнительных измерения такого размера могли бы сыграть роль в проблеме иерархии. Гравитация могла распространиться по эти двум размерностям миллиметрового размера и привести к известному нам слабому гравитационному взаимодействию. Конечно, миллиметр все еще довольно большой размер, но как мы говорили выше, гравитационные тесты не накладывают столь строгих ограничений, как кажется. Окрыленные идеей АДД, физики все больше размышляли о поиске свернутых измерений такого размера.
Если дополнительных измерений больше двух, гравитация модифицируется только на очень малом расстоянии. При большем количестве дополнительных измерений она может быть достаточно ослаблена, даже если такие дополнительные измерения относительно малы. Например, при шести дополнительных измерениях размер должен быть равен всего лишь 10-13 см.
Даже в случае таких малых измерений мы могли бы довольно скоро, если повезет, найти свидетельства в защиту одной из этих моделей, — не в прямых гравитационных тестах, которые мы обсудим в следующем разделе, а в опытах на коллайдерах частиц больших энергий, которые мы рассмотрим позднее.
В поисках больших измерений
Как можно пытаться найти различия в поведении гравитации на малых расстояниях? Что следует искать? Мы знаем, что если существуют свернутые измерения, интенсивность гравитации на расстояниях, меньших, чем размер дополнительных измерений, будет уменьшаться с расстоянием быстрее, чем предсказывал Ньютон, так как гравитация распространяется тогда более чем в трех пространственных измерениях. Когда же тела разделены расстоянием, меньшим размеров дополнительных измерений, становится применимой гравитация в пространстве с дополнительными измерениями. Жук, достаточно маленький для того, чтобы проползти по свернутому в окружность измерению, будет его ощущать, во-первых, потому что он может по нему перемещаться, а во-вторых, потому что гравитационное взаимодействие распространялось бы вокруг него по всем направлениям. Поэтому, если кто-нибудь, вроде этого необычайно чувствительного жука, мог бы регистрировать гравитационное взаимодействие на малых расстояниях, дополнительные измерения имели бы наблюдаемые следствия.
Отсюда вытекает, что, исследуя гравитацию на расстояниях, столь же малых (или меньше), как предполагаемый размер свернутого измерения, и изучая зависимость напряженности гравитационного поля от расстояния между массами на этих расстояниях, можно экспериментально изучить поведение гравитации и найти свидетельство существования дополнительных измерений. Однако эксперименты, чувствительные к гравитации на очень коротких расстояниях, чудовищно трудно поставить. Гравитация так слаба, что она сразу же перекрывается другими взаимодействиями, например электромагнитным взаимодействием. Как отмечалось ранее, к моменту, когда была высказана гипотеза АДД, проводились эксперименты по поиску отклонений от ньютоновского закона тяготения, и было показано, что закон применим по крайней мере до расстояний порядка миллиметра. Если кто-то сумел бы поставить эксперимент лучше и изучить еще более короткие расстояния, то это исследователь имел бы шанс открыть предсказываемые АДД большие измерения, которые находятся как раз на границе экспериментальной доступности.
Экспериментаторы столкнулись с новым вызовом. Руководствуясь идеей АДД, два профессора из Вашингтонского университета, Эрик Адельбергер и Блейн Хекель, поставили красивый эксперимент, целью которого был поиск отклонений от закона Ньютона на очень малых расстояниях. Другие также изучали гравитацию на малых расстояниях, но этот эксперимент был самой строгой проверкой предложения АДД.
Установка, расположенная в подвале физического факультета Вашингтонского университета, получила название эксперимента Эт-Ваш (Еӧt-Wash). Такое название напоминает имя знаменитого венгерского физика, изучавшего гравитацию, барона Роланда фон Этвеша, а с другой стороны, место проведения эксперимента (Вашингтон). Установка группы Эт-Ваш изображена на рис. 76. Она состоит из кольца, подвешенного над двумя притягивающими дисками, расположенными на небольшом расстоянии друг над другом. В кольце, а также в верхнем и нижнем дисках просверлены отверстия, настроенные так, что если закон Ньютона верен, то кольцо не будет поворачиваться. Однако, если существуют дополнительные измерения, разница в гравитационном притяжении между двумя дисками не согласовалась бы с законом Ньютона, и кольцо повернулось бы.
Адельбергер и Хекель не обнаружили никакого закручивания и заключили, что на тех расстояниях, которые они могли изучить, никаких эффектов, связанных с дополнительными измерениями (или иных) и модифицирующих силу тяготения, нет.
Их эксперимент измерил гравитационную силу на расстояниях, меньших, чем когда-либо это удавалось ранее, и установил, что закон Ньютона применим во всем интервале расстояний вплоть до десятой доли миллиметра. Это означало, что дополнительные измерения, даже те, для которых частицы Стандартной модели закреплены на бране, не могут быть размером с миллиметр, как предлагали АДД. Они должны быть по меньшей мере в десять раз меньше.

Примечательно, что измерения миллиметрового размера запрещены также наблюдениями в окружающем нас космическом пространстве. Квантово-механическое соотношение неопределенностей связывает миллиметр с энергией всего лишь порядка 10-3 эВ, а десятую долю миллиметра — с энергией порядка 10-2 эВ, иными словами, с очень малой энергией, например, на много порядков меньшей, чем требуется для рождения электрона.
Частицы с такой малой массой могли бы быть обнаружены в окружающем нас космическом пространстве и в звездных телах, таких как сверхновые или Солнце. Эти частицы были бы настолько легкими, что если бы они существовали, их могла бы рождать горячая сверхновая. Так как мы знаем, насколько быстро охлаждается сверхновая, и понимаем механизм охлаждения (за счет испускания нейтрино), мы знаем, что не может испускаться слишком большого количества других частиц малой массы. Если энергия теряется каким-то иным способом, скорость охлаждения была бы слишком большой. В частности, гравитоны не могут унести слишком много энергии. Рассуждая таким образом, физики показали (независимо от земных экспериментов), что дополнительные измерения должны быть меньше примерно одной сотой миллиметра.
Однако следует иметь в виду, что как бы нас не впечатлял факт отсутствия отклонений от закона гравитации на миллиметровых расстояниях, этот тест непригоден для проверки многих других моделей с дополнительными измерениями. Следует помнить, что только модели с двумя большими дополнительными измерениями приводят к эффектам, которые могли бы быть видимыми в миллиметровом масштабе. Если теория с более чем двумя большими дополнительными измерениями решает проблему иерархии (или если одна из моделей, которые мы рассмотрим в следующей главе, применима к нашему миру), отклонение от закона Ньютона произойдет только на много меньших расстояниях.
Мы не знаем достоверно, на что похоже гравитационное притяжение между двумя телами, находящимися на расстоянии одной десятой миллиметра друг от друга. Никто еще этого никогда не проверял. Так что мы не знаем, откроются ли дополнительные измерения на расстоянии одной десятой миллиметра, что, если подумать, не так уж и мало. Относительно большие дополнительные измерения, хотя и не такие большие, как миллиметр, остаются правдоподобной возможностью. Чтобы проверить такие модели, нам следует подождать коллайдерных тестов. О них речь пойдет в следующем разделе.
Поиски больших дополнительных измерений на коллайдере
Коллайдеры частиц больших энергий хорошо приспособлены для открытия частиц КК, происходящих из больших дополнительных измерений, даже если таких измерений больше двух. В моделях АДД больших дополнительных измерений КК-партнеры гравитона всегда невероятно легкие. Если предположение о больших измерениях применимо к реальному миру, КК-партнеры гравитона должны быть достаточно легкими, чтобы рождаться на ускорителях, независимо от того, сколько имеется дополнительных измерений. Отсюда следует, что даже если размеры измерений меньше миллиметра, современные и будущие поиски на ускорителях должны быть способны их открыть. Современные коллайдеры производят более чем достаточное количество энергии, чтобы создать такие частицы малой массы. На самом деле, если бы единственной существенной величиной была энергия, частицы КК уже рождались бы в изобилии.
Однако здесь возникает загвоздка. КК-партнеры гравитона взаимодействуют чрезвычайно слабо, на самом деле, настолько же слабо, как сам гравитон. Так как взаимодействия гравитона столь пренебрежимо малы, что гравитоны никогда не рождались или детектировались на коллайдерах с измеримой вероятностью, это тем более относится к КК-партнеру гравитона.
Но возможности детектирования частиц КК из дополнительных измерений на самом деле значительно более перспективны, чем это могло показаться вам из сделанной унылой оценки. Дело в том, что если предложение АДД верно, должно быть так много легких КК-партнеров гравитона, что вместе они могут оставить детектируемое свидетельство своего существования. Если сценарий больших измерений верен, то, несмотря на очень редкое рождение отдельных частиц КК, вероятность рождения одной из большого количества легких частиц КК будет измеримо велика. Например, если существует два дополнительных измерения, примерно сто миллиардов триллионов мод КК будут достаточно легкими для того, чтобы рождаться на коллайдере, работающем на энергии порядка ТэВ. Вероятность рождения хотя бы одной из этих частиц будет достаточно велика, даже если вероятность рождения любой отдельно взятой частицы будет очень малой.
Дело обстоит так, как будто вам был сделан намек на что-то в такой тонкой манере, что когда вы в первый раз его услышали, вы не приняли его близко к сердцу. Но после этого пятьдесят человек повторили то же самое. Даже если вы не придали большого значения услышанному в первый раз сообщению, на пятидесятый раз сообщение отложилось у вас в мозгу. Аналогично, хотя легкие частицы КК достаточно легки, чтобы рождаться на современных ускорителях, они взаимодействуют столь слабо, что мы не можем заметить каждую отдельную частицу. Однако, когда ускоритель достигает достаточно высокой энергии, чтобы рождать много таких частиц КК, они оставляют за собой наблюдаемые сигналы.
Если идея АДД верна, то Большой адронный коллайдер (БАК), который будет изучать энергии масштаба ТэВ, сможет рождать частицы КК с измеримой вероятностью. Это может звучать, как счастливое совпадение, — почему, собственно, энергия порядка ТэВ должна иметь отношение к вероятностям рождения частиц КК, когда ни массы частиц КК, ни масса, определяющая интенсивность взаимодействия частиц КК (т. е. МPl), не равны ТэВ? Ответ состоит в том, что энергия порядка ТэВ определяет интенсивность гравитации в пространстве с дополнительными измерениями, а эта гравитация в конце концов определяет, что будет производить коллайдер. Так как взаимодействия многих КК-партнеров гравитона эквивалентны взаимодействию одного гравитона в пространстве с дополнительными измерениями, а такой гравитон сильно взаимодействует при энергиях порядка ТэВ, сумма всех вкладов всех частиц КК должна быть также важной на этом масштабе.
Экспериментаторы уже ищут частицы КК на Тэватроне в Фермилабе. Хотя Тэватрон не достигает энергий, которые будут доступны БАК, он достигает энергий, при которых имеет смысл начать поиск. Но БАК сделает это лучше, и имеет значительно больше шансов обнаружить АДД-частицы КК, если они существуют.
Как будут выглядеть эти частицы? Ответ состоит в том, что соударения, порождающие КК-партнеров гравитона, будут выглядеть как обычные для коллайдера события, за исключением того, что будет казаться, что теряется энергия. На БАК, где сталкиваются два протона, может произойти рождение частицы Стандартной модели и КК-партнера гравитона. Например, частицей Стандартной модели может быть глюон; протоны испытают соударение, образуя виртуальный глюон, а этот виртуальный глюон может, в свою очередь, превратиться в реальный физический глюон и КК-партнер гравитона.
Однако любая индивидуальная частица КК будет взаимодействовать слишком слабо для того, чтобы ее можно было обнаружить; напомним, что КК-партнеры гравитона взаимодействуют очень слабо, и их можно обнаружить только потому, что их очень много. Но поскольку детектор зарегистрирует глюон, или, более аккуратно, струю (см. гл. 7), окружающую глюон, событие, в котором родится КК-партнер гравитона, будет записано, даже если сам КК-партнер гравитона не будет зафиксирован. Ключ к идентификации события, как произошедшего в пространстве с дополнительными измерениями, будет состоять в том, что невидимый КК-партнер унесет энергию в дополнительные измерения, так что будет казаться, что энергия потерялась. Изучая события с одиночными струями, в которых энергия испущенного глюона меньше, чем начальная энергия соударения, экспериментаторы могут заключить, что они родили КК-партнера гравитона (рис. 77). Это аналогично тому, как Паули предсказал существование нейтрино (см. гл. 7).
Так как все, что мы знаем о новой частице, — это тот факт, что она уносит энергию, в действительности мы не можем быть уверены, что ускоритель произвел частицу КК, а не какую-то другую частицу, также слишком слабо взаимодействующую для того, чтобы быть зарегистрированной. Однако, произведя детальные исследования событий с потерянной энергией, например, то, как вероятность образования частиц зависит от энергии, экспериментаторы могут надеяться определить, верна ли интерпретация события как рождение частицы КК.
Частицы КК были бы наиболее доступными посланниками дополнительных измерений в нашем четырехмерном мире, так как они больше всего годятся
на роль легчайших объектов, которые могут сигнализировать о наличии дополнительных измерений. Но, если нам повезет, помимо них могут появиться и другие знаки модели АДД, включающие еще более экзотические объекты. Если АДД правы, гравитация в дополнительных измерениях станет сильной в области порядка ТэВ, что является значительно более низкой энергией, чем та, которая была бы верна в обычном четырехмерном мире. Если дело обстоит именно так, в области энергий порядка ТэВ могли бы рождаться черные дыры, и такие черные дыры из пространства дополнительных измерений открыли бы дорогу к лучшему пониманию классической гравитации, квантовой гравитации и формы вселенной. Если же соответствующие предложению АДД энергии достаточно малы, рождение черных дыр может стать неизбежным; они могут рождаться на БАК.
Черные дыры из дополнительных измерений, которые будут образовываться на коллайдерах, будут намного меньше тех, которые присутствуют в окружающей нас вселенной. Они будут сравнимы по размеру с очень маленькими дополнительными измерениями. Если вы тревожитесь по этому поводу, уверяю вас, что эти малые очень короткоживущие черные дыры не будут представлять для нас или для нашей планеты никакой опасности; они исчезнут прежде, чем смогут чем-то навредить. Черные дыры не существуют вечно, они испаряются, испуская излучение, за счет явления, известного как излучение Хокинга. Точно так же, как маленькая капля кофе испаряется быстрее, чем большая, так и малые черные дыры, которые в принципе могут рождаться на коллайдерах, почти мгновенно испарятся. Тем не менее, если они все же образуются, эти черные дыры из дополнительных измерений будут существовать достаточно долго, чтобы оставить в детекторе видимые следы своего существования. У них будут очень определенные проявления, так как они будут рождать намного больше частиц, чем это обнаруживается при распадах обычных частиц, причем эти частицы будут разлетаться во все стороны.
Кроме того, если модель АДД верна, черные дыры и КК-партнеры гравитона могут быть не единственными экзотическими новыми открытиями. Если теория АДД и теория струн одновременно верны, на коллайдерах могут рождаться струны очень малых энергий, почти достигающих ТэВ. Повторим, что это происходит потому, что фундаментальный гравитационный масштаб в моделях АДД очень низок. Гравитация в пространствах с дополнительными измерениями становится сильной при энергии порядка ТэВ, а квантовая гравитация может привести к измеримым эффектам.
Массы струн в теории АДД даже близко не будут совпадать с недоступным планковским масштабом. Если вы воспринимаете струны как ноты, то струны модели АДД издают значительно более низкие звуки. Низкие звуки в модели АДД будут соответствовать массам не более ТэВ. Если нам повезет, эти массы окажутся достаточно малыми, чтобы их можно было создать на БАК. Соударения с достаточно высокой энергией будут в достаточном количестве рождать легкие струны наряду с новыми объектами, которые называются клубками струн и содержат много длинных струн.
Однако, несмотря на заманчивость таких возможных открытий, следует помнить, что по всей вероятности энергия БАК будет близкой, но не превышающей энергии, необходимой для образования струн и черных дыр. Будут ли струны АДД и черные дыры видимыми, зависит от точного значения энергии многомерной гравитации (и, конечно, от того, верны ли сами предположения).
Последствия
Предложение АДД замечательно. Кто бы мог подумать, что дополнительные измерения могут быть настолько большими или что они могут иметь отношение к проблемам, представляющим непосредственный интерес (по крайней мере для физиков-частичников), например к проблеме иерархии? Однако это предложение на самом деле не решило проблему иерархии. Оно превратило эту проблему в другой вопрос: могут ли дополнительные измерения быть столь большими? Это остается самым главным вопросом в сценарии АДД. Без каких-то новых и до сих пор неустановленных физических принципов нет оснований считать, что измерения будут настолько экстраординарно большими. По крайней мере, согласно современным теориям, нам все еще требуется суперсимметрия, чтобы сохранить большое плоское пространство, необходимое для сценария АДД. По существу, суперсимметрия стабилизирует и укрепляет большие измерения, которые в противном случае сколлапсировали бы. А так как одним из приятных свойств модели АДД является то, что она, как кажется, исключает необходимость суперсимметрии, это несколько разочаровывает.
Другим слабым местом теории являются ее космологические приложения. Для того чтобы теория согласовывалась бы с известными фактами, касающимися эволюции Вселенной, нужно тщательно выбрать ряд ее параметров. При этом балк должен содержать слишком мало энергии, в противном случае, космологическая эволюция не будет согласовываться с наблюдениями. Конечно, все это возможно, но весь смысл решения проблемы иерархии состоит в том, чтобы исключить необходимость большой подгонки.
Тем не менее многие физики склонны всерьез воспринимать теории с дополнительными измерениями и пытаются изобретать пути их поиска. Экспериментаторы были особенно возбуждены. Как мне сказал работающий в Фермилабе физик-частичник Джо Ликкен, описывая реакцию экспериментаторов на большие дополнительные измерения: «Да они все свихнулись на этих „поисках за рамками Стандартной модели“. Суперсимметрия или дополнительные большие измерения? Какая разница! Дополнительные измерения не большее сумасшествие». Экспериментаторы изголодались по поискам чего-то нового, а дополнительные измерения сулят очень интересную альтернативу суперсимметрии.
Реакция теоретиков была более неоднородной. С одной стороны, большие дополнительные измерения выглядят очень странно; ранее никто никогда их не рассматривал, так как ни у кого не было никакой причины, почему дополнительные измерения должны быть так велики. С другой стороны, никто не мог найти способ от них оказаться. На самом деле, прежде чем была написана первая статья о больших дополнительных измерениях, один из ее авторов Гия Двали докладывал о них в Станфорде. Авторы, которые вполне понимали радикальный характер их предложения, ожидали доклада с трепетом, и успокоились, когда не было сделано никаких серьезных замечаний. Но они были также немного испуганы — как люди могли принять эту достаточно радикальную идею с таким спокойствием? Нима сказал мне, что аналогичная реакция была и тогда, когда они впервые выложили свою статью в Интернете. Хотя они ожидали потока откликов, получили всего два. По-видимому, итальянский физик Рикардо Ратацци и я были единственными, кто сделал замечания по ряду возможных проблем. Но даже эти два отклика не были, на самом деле, независимыми: Рикардо и я только что обсуждали эту работу в ЦЕРНе, где мы оба находились по приглашению.
Постепенно, проникаясь приложениями модели АДД, физики начали более детально исследовать следствия этой модели для реального мира, включая тестирование гравитации, поиски на ускорителях, астрофизические следствия и космологические приложения. Реакция менялась в зависимости от исследовательских интересов или стиля.
Физики, исследования которых опирались на детали Стандартной модели, были счастливы получить возможность разработки новой идеи, которая в любом случае была интересной. Удивительно, что определенная враждебность исходила от некоторых моделестроителей, которые не хотели проститься с идеями о суперсимметрии, укоренившимися за последние годы. Правда, следует признать, что столь драматичное изменение Стандартной модели стало серьезным вызовом. Каждая новая модель должна воспроизводить те свойства Стандартной модели, которые уже были экспериментально проверены, и теориям, которые столь сильно меняют Стандартную модель, надо принять этот вызов. Кроме того, сияющая вершина суперсимметрии — объединение констант, т. е. тот факт, что при большой энергии все взаимодействия будут иметь одинаковую интенсивность, также должна быть стерта. Однако более молодые теоретики, не столь преданные суперсимметрии, были сильно воодушевлены. Дополнительные измерения были свежей, необъезженной идеей, бросающей новые вызовы и ставящей открытые вопросы.
Реакция со стороны теоретиков-струнников также была смешанной. Когда Савас Димопулос приступил к работе над своим проектом, он предвидел, что изучение дополнительных измерений приведет к более тесному объединению теории струн и физики частиц. И теоретики-струнники обратили внимание на работу, хотя большинство из них рассматривали большие дополнительные измерения как интересную идею, которая никогда не будет иметь отношения к теории струн. Для теоретиков-струнников главная проблема была теоретической: очень трудно понять, каким образом измерения могут быть настолько большими, как предполагается в схеме АДД.
Лично я не верила, что дополнительные измерения, даже если они существуют, окажутся столь большими[150]. И по теоретическим причинам (трудно получить измерения, которые столь велики), и по экспериментальным (очень трудно получить работающую космологию), идея выглядит как общий план. Даже Нима, один из адептов идеи, высказывает в этом месте сомнения. Но это была очень важная теоретическая идея. Это новое, ранее не исследовавшееся предложение высветило размеры нашего незнания о гравитации и форме вселенной. Работа АДД стимулировала много новых мыслей, и окажется ли она правильной или нет, она уже оказала важное влияние на мысли физиков. Сценарии с большими измерениями привели к множеству новых предложений по дополнительным измерениям, и предложили много идей для экспериментальной проверки. После того как заработает БАК, теоретические предубеждения будут отброшены, так как следствия точных данных будут неопровержимыми. Кто знает? Они могут оказаться правы.
Что нового
• Если частицы Стандартной модели закреплены на бране, дополнительные измерения могут быть намного больше, чем ранее думали физики: размер этих измерений может быть порядка десятой доли миллиметра.
• Дополнительные измерения могут быть настолько большими, что они могут объяснить, почему тяготение настолько слабее электромагнитного, слабого и сильного взаимодействий.
• Если большие дополнительные измерения решают проблему иерархии, гравитация в пространстве больших дополнительных измерений может стать сильной при энергии порядка ТэВ.
• Если гравитация в пространстве с дополнительными измерениями становится сильной при энергии порядка ТэВ, то БАК будет рождать частицы КК с измеримой вероятностью. Частицы КК будут уносить энергию соударения, так что их сигнатурой (характерным признаком) будут события с потерявшейся энергией.
Глава 20
Закрученный пассаж: решение проблемы иерархии
What’s so small to you,
Is so large to me.
If it’s the last thing I do,
I’ll make you see.
Suzanne Vega[151]
Афина вздрогнула и проснулась. К ней снова и снова возвращался тот сон, когда за входом в кроличью нору ее ждал сказочный мир. Но сейчас, когда Кролик объявил: «Следующая остановка — Двумерная страна», Афина не шелохнулась и стала ждать, что же будет дальше.
На остановке в трех пространственных измерениях Кролик объявил: «Если Вы здесь жили, то сейчас окажетесь дома». Но он отказался открыть двери, несмотря на заявления Афины, что она действительно живет здесь и очень хочет вернуться домой.
На следующей остановке попытались войти одетые в униформу шестимерщики. Но Кролик бросил взгляд на их непомерно раздавшиеся тела и резко закрыл двери, говоря, что они вряд ли поместятся, они быстро удалились, после того как Кролик пригрозил обтесать их со всех сторон[152].
Лифт продолжал свое необычное движение. Когда он опять остановился, кролик объявил: «Закрученная геометрия — пятимерный мир»[153]. Он ласково подтолкнул Афину к двери и посоветовал: «Войди в комнату смеха — тебя вернут домой». Так как Кролик упомянул пятое измерение, Афине это показалось маловероятным. Но у нее не было никакого выбора, кроме как войти и надеяться на правоту хитрого Кролика.
Когда вы изучаете иностранный язык, слова, которые вы запоминаете, зависят от ваших конкретных нужд или интересов. Например, во время велосипедного путешествия по Италии, я научилась множеству разных способов просить воды — aqua di rubinetto, aqua minerale, aqua (minerale) gassata, aqua (minerale) naturale и т. п. Аналогично, изучая новые физические сценарии, каждый физик имеет свои собственные представления и собственные вопросы и может поэтому обратить внимание на определенный ряд свойств системы или обнаружить разные приложения того, что уже известно. Каждый из нас может услышать что-то свое, даже когда он сталкивается с теми же словами или ситуациями. Имеет смысл внимательно слушать.
Раман и я размышляли над проблемой иерархии в течение многих лет. Но когда мы начали свое сотрудничество, мы не искали нового, лучшего решения этой проблемы. Мы работали над моделью уединенного нарушения суперсимметрии, которую я описала в гл. 17. В процессе этой работы мы случайно обнаружили замечательную закрученную геометрию пространства-времени (частный тип искривленной геометрии, о которой я вскоре расскажу), ограниченного двумя бранами. Поскольку Раман и я занимались физикой частиц и слабостью гравитационного взаимодействия, мы немедленно поняли потенциальную важность закрученной геометрии: если Стандартная модель физики частиц «живет» в этом пространстве-времени, проблема иерархии может быть решена. Я не уверена, что мы были первыми, изучившими эту конкретную систему уравнений Эйнштейна. Но мы, безусловно, были первыми, кто осознал, что она имеет поразительные последствия.
Следующие несколько глав поясняют эту и другие примечательные возможности искривленного пространства-времени и то, как эти следствия иногда не соответствуют нашим ожиданиям. В этой главе внимание сосредоточено на закрученном пятимерном мире, который может помочь объяснить огромный диапазон масс в физике частиц. В то время как в четырехмерной квантовой теории поля частицы обычно имеют примерно одинаковые массы, в закрученной многомерной геометрии это уже не так. Закрученные геометрии определяют структуру, в которой очень естественно возникают несоизмеримые массы, а квантовые эффекты находятся под контролем.
В конкретной геометрии, описанной в этой главе, мы увидим, что пространство так сильно скручено в присутствии двух плоских граничных бран, что проблема иерархии в физике частиц автоматически решается, не требуя присутствия большого измерения или какого-то другого большого числа. В этом сценарии одна брана испытывает действие большой силы гравитации, а другая не испытывает этого действия вообще. Вдоль пятого измерения пространство-время изменяется так быстро, что оно превращает скромное число, связанное с расстоянием между двумя бранами, в огромное число (порядка десяти миллионов миллиардов), связанное с относительной интенсивностью гравитационного взаимодействия.
Сначала мы объясним слабость гравитации на второй бране в терминах функции вероятности гравитона, определяющей взаимодействия гравитона на любом заданном расстоянии в пятом измерении. Но мы объясним также слабость гравитации иными терминами, основанными на закрученной геометрии, а не на интенсивности гравитационного взаимодействия. Мы увидим, что одним из поразительных следствий закрученной геометрии является то, что размер, масса и даже время зависят от положения вдоль пятого измерения. Закручивание пространства и времени в этой установке из двух бран похоже на закручивание времени вблизи горизонта черной дыры. Но в этом случае время замедляется, геометрия расширяется и на одной из бран частицы приобретают малые массы, так что проблема иерархии автоматически решается.
После обсуждения закрученной геометрии и ее приложений к проблеме иерархии, мы завершаем эту главу обсуждением характерных для будущих экспериментов следствий теории. Одним из самых волнующих вопросов этой теории, как и вопросов о моделях с большими дополнительными измерениями, обсуждавшихся в предыдущей главе, является то, что если она верна, она очень скоро будет иметь экспериментальные следствия на ускорителях частиц. На самом деле мы увидим, что эти следствия будут даже более существенными, чем обсуждавшаяся нами характерная недостающая энергия. КК-партнеры гравитона, хоть и являясь гостями из многомерного пространства, будут различимыми, видимыми частицами, распадающимися на знакомые частицы на нашей четырехмерной бране.
Закрученная геометрия и ее удивительные приложения
Геометрия, которую мы рассматриваем в этой главе, содержит две браны, ограничивающие пятое измерение пространства, как показано на рис. 78. Эта система похожа на рассмотренную в гл. 17 тем, что имеются две браны и пятое измерение, простирающееся между ними. Однако на самом деле это совершенно другая теория. Частицы и распределение энергии различны, и теория не супер-симметрична. Тем не менее, как и в том случае, мы предполагаем, что все частицы Стандартной модели вместе с хиггсовской частицей, ответственной за нарушение электрослабой симметрии, закреплены на одной из бран.

Как и ранее, в этой схеме мы предполагаем, что гравитация — единственное взаимодействие, существующее внутри пятого измерения. Это означает, что, если не считать гравитацию, то каждая из бран выглядела бы как общепринятая четырехмерная вселенная. Калибровочные бозоны и частицы, расположенные на бранах, будут передавать взаимодействия и взаимодействовать друг с другом так, как будто не существует никакого пятого измерения. Частицы Стандартной модели будут перемещаться только по трем плоским пространственным измерениям на бранах, а взаимодействия будут распространяться только вдоль плоской трехмерной поверхности браны.
Однако гравитация отличается от других взаимодействий, так как она не прикреплена к бране, а напротив, существует в полном пятимерном балке. Гравитационное взаимодействие будет ощущаться везде в пятом измерении. Но это не означает, что оно ощущается везде одинаково. Энергия на бранах и в пятимерном балке искривляет пространство-время, что приводит к колоссальной разнице в значении гравитационного поля.
Теории с большими дополнительными измерениями из предыдущей главы использовали тот факт, что браны могут удерживать частицы и взаимодействия, но пренебрегали энергией, которую могут нести сами браны. Мы с Раманом не были уверены, что это предположение всегда хорошее, так как главной составной частью общей теории относительности Эйнштейна является то, что энергия индуцирует гравитационное поле, и это означает, что когда браны переносят энергию, они должны искривлять пространство и время. Во вселенной с единственным дополнительным измерением, которую мы собирались изучать, было совершенно не ясно, можно ли пренебречь энергией браны и балка: гравитационные эффекты браны не рассеиваются очень быстро, так что даже очень далеко от бран можно ожидать искажений пространства-времени.
Мы хотели узнать, каким образом пространство-время будет искривляться при наличии двух несущих энергию бран, которые ограничивают дополнительное измерение пространства. Раман и я решили эйнштейновские уравнения гравитации для такой схемы с двумя бранами, предполагая, что в балке и на бранах содержалась энергия. Мы обнаружили, что такая энергия была действительно очень важной — результирующее пространство-время было резко искривлено.
В ряде случаев искривленные пространства легко изобразить на картинке. Например, поверхность сферы двумерна — для того чтобы знать свое положение, вам требуются только широта и долгота, — но тем не менее она явно искривлена. Однако многие искривленные пространства труднее нарисовать, так как они не могут быть легко представлены в трехмерном пространстве. Конкретное закрученное пространство-время, которое мы сейчас будем рассматривать, является примером такого пространства. Это часть пространства-времени, известная как пространство анти-де Ситтера. Кривизна этого пространства отрицательна, так что оно напоминает скорее не сферу, а чипсы «Прингле». Это пространство получило свое название по имени датского математика и космолога Виллема де Ситтера, изучавшего пространство с положительной кривизной, которое сейчас называется пространством де Ситтера. Хотя нам эти названия здесь не понадобятся, мы сошлемся на них позднее, когда свяжем эту теорию с теорией пространства анти-де Ситтера, которое изучают теоретики-струнники.
Ниже мы рассмотрим интересный подход, в котором пятимерное пространство-время искривлено. Но для начала сосредоточимся на двух бранах на краях пятого измерения. Эти две граничные браны совершенно плоские. Находясь на бране на любой из границ, вы будете прикреплены к (три + один) — мерному миру (три пространственных измерения и одно временное)[154], который будет простираться бесконечно далеко по трем пространственным измерениям и выглядеть как плоское пространство-время, без особых гравитационных эффектов.
Кроме того, искривленное пространство-время обладает тем специальным свойством, что если вы ограничитесь любым отдельным срезом вдоль пятого измерения, но не самими бранами на краях, вы обнаружите, что этот срез совершенно плоский. То есть, хотя нигде в пятом измерении за исключением концов нет бран, геометрия (три + один) — мерных поверхностей, которые вы получаете, находясь в какой-либо пятимерной точке, выглядит плоской, т. е. имеет ту же форму, что и большие плоские браны на границах. Если вы рассматриваете граничные браны как горбушки у буханки хлеба, то плоские параллельные четырехмерные области в любой точке вдоль пятого измерения пространства-времени похожи на плоские, нарезанные куски хлеба из внутренней части буханки.
Но тем не менее рассматриваемое нами пятимерное пространство искривлено. Это отражается в том способе, которым четырехмерные плоские срезы пространства-времени склеены вместе вдоль пятого измерения. Впервые я говорила об этой геометрии в институте теоретической физики Кавли в Санта-Барбаре, где теоретик-струнник Том Бэнкс объяснил мне, что с технической точки зрения пятимерная геометрия, которую нашли Раман и я, называется закрученной. Хотя многие искривленные геометрии пространства-времени в разговорной речи называются закрученными, технический термин относится к геометриям, в которых каждый срез плоский[155], но они собираются вместе с учетом общего закручивающего конформного фактора. Этот фактор есть функция, меняющая общий масштаб для положения, времени, массы и энергии в каждой точке в пятом измерении. Такое замечательное свойство закрученной геометрии достаточно тонкое, и я объясню его позднее в следующем разделе. Конформный фактор сказывается также на функции вероятности гравитона и взаимодействиях, которые мы вскоре изучим.
Искривленное пространство с плоскими слоями изображено на рис. 79. Это заполненная воронка. Мы могли бы с помощью большого ножа нарезать воронку на плоские листки, но поверхность воронки явно искривлена. В некоторых отношениях это похоже на искривленное пространство-время, которое мы рассматриваем. Но аналогия не идеальна, так как граница воронки, ее поверхность есть единственное место, где она искривлена, в то время как в закрученном пространстве-времени кривизна есть везде. Эта кривизна отражалась бы в общем изменении масштаба измерительной линейки в пространстве и скорости хода часов для времени, которые будут разными в каждой точке пятого измерения.
Более простой способ проиллюстрировать кривизну закрученного пространства-времени — обратиться к форме функции вероятности гравитона. Гравитон — это частица, переносящая гравитационное взаимодействие, и его функция вероятности говорит нам о вероятности обнаружения гравитона в любой фиксированной точке пространства. Интенсивность гравитации отражается в этой функции: чем больше ее значение, тем сильнее взаимодействия гравитона в этой конкретной точке и тем сильнее сила тяготения.

Для плоского пространства-времени гравитон будет с равной вероятностью обнаруживаться везде. Функция вероятности для гравитона в плоском пространстве-времени была бы поэтому постоянной. Но для искривленного пространства-времени, как и для закрученной геометрии, которую мы рассматриваем, это уже будет не так. Кривизна говорит нам о форме гравитации. Когда пространство-время искривлено, значение функции вероятности гравитона различно в разных местах пространства-времени.
Так как каждый срез пространства-времени в нашей закрученной геометрии совершенно плоский, функция вероятности гравитона не изменяется вдоль трех стандартных пространственных измерений, а меняется только вдоль пятого измерения[156]. Иными словами, даже несмотря на то, что функция вероятности гравитона имеет разные значения в разных местах вдоль пятого измерения, до тех пор пока две точки равноудалены вдоль пятого измерения, значение этой функции будет одним и тем же. Это говорит нам, что функция вероятности гравитона зависит только от положения в пятом измерении. Тем не менее она полностью характеризует кривизну закрученного пространства-времени. И так как эта функция изменяется только вдоль одной координаты, т. е. вдоль пятого измерения, ее просто изобразить на рисунке.
Функция вероятности гравитона вдоль пятого измерения изображена на рис. 80. Она экспоненциально быстро (т. е. необычайно быстро) убывает, как только мы покидаем первую брану, которую мы назовем Гравитационной браной, и направляется в сторону второй браны, которую мы назовем Слабой браной. Гравитационная брана и Слабая брана различны, так как первая несет положительную энергию, а вторая несет отрицательную энергию. Такое распределение энергии приводит к тому, что функция распределения гравитона намного больше в окрестности Гравитационной браны.
Эффект падения функции вероятности состоит в том, что гравитон, физическая частица, обмен которой генерирует гравитационное притяжение, имеет очень мало шансов быть найденным вблизи Слабой браны. Поэтому взаимодействия гравитона на Слабой бране сильно подавлены.
Интенсивность гравитации так сильно зависит от положения в пятом измерении, что интенсивности гравитационного взаимодействия на двух бранах, ограничивающих противоположные концы такого закрученного пятимерного мира, очень сильно различаются. Гравитация сильна на первой бране, где гравитация локализована, но очень слаба на второй бране, где находится Стандартная модель. Так как функция вероятности гравитона пренебрежимо мала на второй бране, взаимодействия гравитона с захваченными здесь частицами Стандартной модели оказываются чрезвычайно слабыми.
Отсюда следует, что в таком закрученном пространстве-времени мы действительно можем ожидать иерархии между наблюдаемым массами и планковским масштабом масс. Хотя гравитон есть везде, интенсивность его взаимодействия с частицами на Гравитационной бране много больше, чем с частицами на Слабой бране. Функция вероятности гравитона на Слабой бране необычайно мала, и если этот сценарий есть правильное описание мира, такая малость ответственна за слабость гравитации в нашем мире.
В этой модели ничтожная гравитация на Слабой бране не требует большого расстояния между двумя бранами. Как только вы покидаете Гравитационную брану, где сильно сконцентрирована функция вероятности гравитона, гравитация становится экспоненциально малой, что приводит к необычайной малости гравитации на Слабой бране. Так как функция вероятности гравитона стремительно уменьшается, гравитация на Слабой бране (где мы живем) резко уменьшается. Она может быть в 1015 раз слабее, чем можно ожидать без учета закручивания, даже если две браны расположены довольно близко. Этот аспект теории, тот факт, что бранам не нужно быть разделенными слишком сильно, делает эту модель намного более реалистичной возможностью, чем модель больших дополнительных измерений. Хотя большие дополнительные измерения были привлекательной переформулировкой проблемы иерархии, в конце концов в них все еще присутствует необъясненное большое число — размер дополнительного измерения. В теории, которую мы сейчас рассматриваем, гравитационное взаимодействие на Слабой бране на много порядков величины слабее всех других взаимодействий, даже когда Слабая брана удалена от первой браны (Гравитационной браны) на очень скромное расстояние.
Расстояние между бранами в такой закрученной геометрии должно быть лишь чуть-чуть больше планковского масштаба длины. В то время как сценарий больших измерений требует введения очень большого числа, а именно размера измерений, в модели с закрученной геометрией для объяснения иерархии никакого неестественно большого числа не требуется. Это происходит потому, что экспонента автоматически превращает скромное число в очень большое число (экспоненту), или в очень малое число (обратное большой экспоненте). На Слабой бране интенсивность гравитации меньше; она уменьшается на фактор, являющийся экспонентой от расстояния между двумя бранами[157]. Если Слабая брана находится на расстоянии в 16 единиц от другой[158], ожидается огромное отношение между планковским масштабом масс — большой массой, говорящей нам, что гравитация слаба, — и массой хиггсовской частицы, а следовательно, массами слабых калибровочных бозонов. Это означает, что для того, чтобы объяснить иерархию, достаточно расстояния между бранами, которое всего в шестнадцать раз больше ваших самых наивных оценок. Множитель 16 может показаться большим, но он все же значительно меньше числа 1016, которое мы пытаемся объяснить.
В течение многих лет физики-частичники надеялись найти экспоненциальное объяснение иерархии. Иначе говоря, мы надеялись обнаружить, что это необъяснимо большое число является следствием некоторой естественно возникающей экспоненциальной функции. Теперь Раман и я с помощью дополнительных измерений нашли способ, которым физика частиц автоматически включила экспоненциальную иерархию масс. В том месте, где находится наша брана (Слабая брана), гравитационное взаимодействие может быть много меньше, чем оно было бы там, где функция вероятности гравитона достигает максимума. Так как гравитация на нашей бране должна быть ослаблена закрученной геометрией, если Стандартная модель квартирует на Слабой бране, то проблема иерархии будет решена. Это было решение проблемы иерархии, и оно падало прямо нам в руки.
Другой способ понять это примечательное новое свойство закрученной геометрии — рассмотреть, как ослабляется гравитация. В гл. 19 мы объяснили слабость гравитации в сценарии АДД с помощью идущих от массивного тела гравитационных силовых линий, которые разбавляются, распространяясь по большим измерениям. Если мы выбираем этот путь, мы должны описать такое разбавление как следствие функции вероятности гравитона. Напомним, что функция вероятности гравитона показывает, как гравитация распространяется по пространству. Так как гравитация в сценарии больших дополнительных измерений в равной степени сильна везде в дополнительных измерениях, в этом случае функция вероятности гравитона плоская. Такая плоская функция вероятности гравитона показывает, что гравитон, частица, переносящая гравитацию, размазана по большому пространству, окруженному дополнительными измерениями. Такая плоская функция вероятности, равномерно распределенная по всему пространству дополнительных измерений, говорит, что влияние гравитации в четырех измерениях сильно ослабилось.
У закрученного пятимерного пространства-времени, которое мы сейчас рассматриваем, имеется интересная особенность. Гравитон уже больше не с равной вероятностью находится во всех местах пятимерного пространства, лежащих между двумя границами, Гравитационной браной и Слабой браной. Распределение гравитона на самом деле далеко не демократично, что является автоматическим следствием определенного распределения энергии на бранах и в балке. Функция вероятности гравитона изменяется: она велика в одной области и мала во всех остальных, и именно это изменение обеспечивает фактор ослабления, ответственный за то, что гравитация столь слаба в нашем мире. Гравитация ничтожна на Слабой бране, так как функция вероятности гравитона на ней ничтожна.
Вернемся ненадолго к аналогии с разбрызгивателем, которую мы использовали ранее для объяснения того, каким образом интенсивность гравитации уменьшается с расстоянием. Чем больше область, над которой разбрызгиватель распределяет воду (показано на верхней части рис. 81), тем более разжижена струя воды. Если существуют большие дополнительные измерения, гравитация распределяется по очень большой области и тоже ослабляется. Поэтому в низкоэнергетической эффективной четырехмерной теории гравитация кажется слабой.

Закрученная геометрия, в свою очередь, напоминает разбрызгиватель, который не распределяет воду равномерно по всем направлениям, а вместо этого подает ее выборочно в одну конкретную область вокруг Гравитационной браны (см. нижнюю часть рис. 81). При таком недемократичном разбрызгивателе очевидно, что во все области, кроме любимой, будет доставляться меньше воды. И если количество воды, подающееся в другие области, падает экспоненциально от любимого места, доля воды, доставленная к другим областям, будет действительно очень малой, даже если все они будут на небольшом расстоянии друг от друга. Ясно, что вода, доставленная «закрученным» разбрызгивателем, «разбавляется» намного больше, чем вода, равномерно распределенная по всем областям.
Итог состоит в том, что если все частицы Стандартной модели размещены на Слабой бране, то гравитация так слаба по сравнению с другими тремя взаимодействиями, что проблема иерархии в физике частиц — вопрос о том, почему гравитация так слаба по сравнению с другими взаимодействиями — решен. Слабая гравитация есть естественное следствие малой амплитуды функции вероятности гравитона на Слабой бране, даже если она находится на сравнительно небольшом расстоянии (примерно в десять раз больше, чем любимый теорией струн планковский масштаб длины) от Гравитационной браны.
Увеличение и уменьшение в закрученном измерении
Предыдущее объяснение иерархии с помощью экспоненциально падающей функции вероятности полностью адекватно пониманию закрученного пространства-времени. Интуитивное объяснение слабости гравитации сводится к тому, что гравитон с меньшей вероятностью обнаруживается на Слабой бране. Вы можете принять это объяснение и перейти к следующему разделу, но, возможно, вас заинтересует чут^ более строгое объяснение, в котором более тщательно изучаются поразительные свойства закрученного пространства-времени.
В этом разделе мы увидим, что слабость гравитации на Слабой бране можно объяснить также как следствие существования объектов, становящихся больше и легче по мере удаления от Гравитационной браны и приближения к Слабой бране. Если бы Афина двигалась от Гравитационной браны к Слабой бране (как это она сделает в истории в следующей главе), она бы увидела, как ее тень на Гравитационной бране при удалении от браны увеличивается в размерах. При этом увеличение размеров ее тени огромно — она вырастет на шестнадцать порядков величины!
Мы увидим также, что в этой геометрии тяжелые и легкие частицы могут мирно сосуществовать. Даже когда на одной из двух бран имеются частицы планковского масштаба масс, на другой имеются только частицы слабого масштаба масс. Поэтому проблемы иерархии больше не существует.
Чтобы понять, как все это устроено, предположим, что, как и большинство людей (по крайней мере тех, кто не читал эту книжку), вы совершенно ничего не знаете о пятом измерении, которое ко всему еще невидимо. Непоколебимые в своем убеждении, что вы живете в четырех измерениях, вы будете знать только о четырехмерной гравитации, которая, как вы считаете, передается обычным четырехмерным гравитоном. В четырехмерной эффективной теории, описывающей то, что вы видите, будет только одно гравитационное взаимодействие, следовательно, только один тип четырехмерного гравитона. Но этот гравитон не будет содержать никакой информации о местонахождении частицы в исходной теории с дополнительным измерением.
Рассуждая таким образом, кажется будто все взаимодействия гравитонов должны быть одинаковы, т. е. независимы от того, где в пятом измерении изначально был объект. В конце концов, вы не можете знать, что объект пришел изначально из пятого измерения, или даже что пятое измерение было. Ньютоновская гравитационная постоянная, определяющая интенсивность взаимодействия гравитона, была бы единственной величиной, определяющей интенсивность всех четырехмерных гравитационных взаимодействий. Но в предыдущем разделе мы видели, что гравитационное взаимодействие слабеет, когда вы двигаетесь от Гравитационной браны к Слабой бране. Тогда возникает вопрос, каким образом интенсивность гравитации осуществляет сбор информации о местонахождении объекта в пятом измерении?
Решение кажущегося парадокса связано с тем фактом, что гравитационное взаимодействие также пропорционально массе, а масса в разных точках вдоль пятого измерения может и должна быть разной. Единственный способ воспроизвести слабеющее взаимодействие гравитона на каждом последующем срезе вдоль пятого измерения заключается в том, чтобы измерить массу порознь на каждом четырехмерном срезе.
Одно из многих примечательных свойств закрученного пространства-времени состоит в том, что, когда вы двигаетесь от Гравитационной браны к Слабой бране, энергии и импульсы уменьшаются. Уменьшающиеся энергии и импульсы (а также совместимость с квантовой механикой и специальной теорией относительности) говорят нам, что должны расширяться расстояние и время (рис. 82). В описываемой сейчас геометрии размер, время, масса и энергия зависят от места. Четырехмерные размеры и массы наследуют значения, зависящие от их исходных положений в пятом измерении. Физика выглядит четырехмерной. Но линейка, с помощью которой измеряется длина, или масштаб, с помощью которого измеряется масса, зависит от начального пятимерного местоположения. Жители Гравитационной браны или Слабой браны видят четырехмерную физику, но они будут измерять разные размеры и разные значения масс.
Гравитационное притяжение масс частиц, находящихся на большем расстоянии от Гравитационной браны в первоначальной пятимерной теории, становится меньше в четырехмерной эффективной теории, так как сами массы становятся меньше. Это происходит потому, что в каждой точке в пятом измерении масса и энергия изменяют масштаб в число раз, пропорциональное амплитуде функции вероятности гравитона в этой конкретной точке. При этом конформный фактор, равный той величине, во сколько раз вы изменяете масштаб энергий, при удалении от Гравитационной браны становится меньше. На самом деле график конформного фактора имеет в точности ту же форму, что и функция вероятности гравитона. Поэтому массы и энергии уменьшаются в разное число раз в каждой точке вдоль пятого измерения, причем конформный фактор определяет, во сколько именно.

Такое изменение масштаба может показаться произвольным, но это не так. Однако это вопрос тонкий, поэтому сначала рассмотрим аналогию. Предположим, что мы собираемся измерить время в единицах длительности поездки в 100 км на поезде. Я буду называть эти единицы ПВ (поездное время). Это прекрасная единица измерения времени с одним только недостатком, что ваше определение времени будет зависеть от того, где вы путешествуете: быстрые там поезда или нет? Например, предположим, что кинокартина длится 2 часа. Если американский поезд затрачивает один час, чтобы преодолеть 100 км, американский зритель проедет 200 км, пока посмотрит фильм, и скажет, что фильм длился 2 ПВ. С другой стороны, французский зритель, едущий на экспрессе, подумает, что фильм длился 6 ПВ, так как экспрессы во Франции едут примерно в три раза быстрее, и французскому зрителю придется смотреть свой DVD во время 600-километрового пути, чтобы понять, чем все закончится. Так как поезд французского зрителя проходит 100 км за 20 мин, в то время как американский поезд покрывает то же расстояние за 1 час, вам нужно изменить масштаб поездного времени, если американцы и французы должны использовать одинаковые единицы и согласны измерять длительность кино в единицах ПВ. Чтобы перевести время от французского к американскому, вам необходимо изменить масштаб французского поездного времени на множитель три.
Аналогично, на Слабой бране, где взаимодействие гравитона намного слабее, чем на Гравитационной бране, единицы масштаба, используемого для измерения энергии, должны быть изменены, чтобы учесть слабость гравитации. На Слабой бране изменение масштаба должно быть произведено в колоссальное число раз, равное 1016. Это означает, что в то время как на Гравитационной бране можно ожидать, что все фундаментальные массы равны МPl (планковский масштаб масс), на Слабой бране они будут только порядка 1000 ГэВ, т. е. в 1016 раз меньше. Массы новых частиц, живущих на Слабой бране, могут быть несколько больше, от 3000 до 5000 ГэВ, но они не должны быть много больше, так как все массы чрезвычайно сильно изменили масштаб.
Проблема иерархии возникает тогда, когда все массы оказываются около самой большой массы. Если эта масса есть планковский масштаб масс, то можно ожидать, что все массы будут такими же большими, как планковский масштаб масс. Но благодаря изменению масштаба, если вы первоначально полагали, что планковский масштаб масс был ожидаемой массой для всего на Гравитационной бране, тогда вы должны заключить, что ожидаемой массой на Слабой бране будет ТэВ, на 16 порядков меньшая масса[159]. Это означает, что масса хиггсовской частицы не столь ужасна; ожидается масса порядка ТэВ, даже несмотря на то, что гравитация слаба. Изменение масштаба, существенное в этой интерпретации, решает проблему иерархии.
По тем же соображениям, все новые объекты на Слабой бране, включая струны, должны иметь массу порядка ТэВ. Отсюда следует, что такая модель будет иметь впечатляющие экспериментальные следствия. На Слабой бране дополнительные частицы, связанные со струнами, будут намного легче, чем частицы на Гравитационной бране, или, если угодно, в четырехмерном мире. Слабая брана представляет сказочный сценарий в контексте обнаружения дополнительных измерений. Если эта идея правильна, то частицы малой массы из дополнительных измерений находятся почти рядом. Частицы ТэВной массы в изобилии имеются на Слабой бране.
Ожидается, что масса всего, что находится на Слабой бране, меньше планковского масштаба масс на фактор 1016. Но согласно квантовой механике, меньшая масса означает больший размер. Тень Афины будет расти, когда она пойдет от Гравитационной браны в сторону Слабой браны. Это указывает, что струны на Слабой бране не должны иметь размер 10-33 см. Напротив, они должны также быть на 16 порядков величины больше, т. е. иметь размер порядка 10-17 см.
Хотя я сконцентрировала внимание на сценарии двух бран с конкретным конформным фактором, рассмотренные свойства, похоже, являются более общими. С учетом дополнительных измерений есть основания ожидать несопоставимых масс. Интуитивные представления физики частиц о том, что массы должны быть более или менее одинаковые, нарушается, и ожидается появление широкого диапазона масс. Находящиеся в разных местах частицы будут, естественно, иметь разные массы. Их тени меняются, если вы перемещаетесь в другое место. В нашем четырехмерном мире результатом будет широкий диапазон размеров и масс, и все это мы будем наблюдать.
Дальнейшие исследования
Когда в 1999 году появилась наша статья, объясняющая иерархию с помощью закрученной геометрии, большинство наших коллег не заметило, что это была по-настоящему новая теория, сильно отличающаяся от идеи больших измерений. Джо Ликкен сказал мне: «Реакция наступила медленно. В конце концов каждый понял, что эта работа (и еще одна, которую я поясню в гл. 22) очень важная, новая и плодотворная, открывающая целую новую арену идей. Но случилось это не сразу».
В течение месяцев после выхода нашей работы в свет меня просили сделать доклады о моей работе по «большим дополнительным измерениям». Я пыталась возражать, что вся красота нашей теории как раз в том, что измерения небольшие! А Марк Вайс (какое удачное имя),[160] теоретик в области физики частиц из Калтеха, много смеялся над заголовком, который был дан моему пленарному докладу на заключительном заседании Конференции по лептонам и фотонам в 2001 году, главной конференции по физике частиц, на которой экспериментаторы представляют важные результаты. Организаторы дали моему докладу название, которое имело отношение ко всем работам по дополнительным измерениям, кроме моей собственной!
Марк и его тогдашний студент Вальтер Гольдбергер были первыми, кто поняли преимущества закрученного сценария. Но они также заметили, что Раман и я оставили потенциальный пробел в наших результатах, который следовало заполнить. Мы предполагали, что динамика бран естественным путем приведет к бранам, находящимся на умеренном расстоянии друг от друга. Однако мы не показали явно, как устанавливается расстояние между двумя бранами. Это не просто деталь; роль нашей теории как решения проблемы иерархии зависела от способности быстро стабилизировать две браны на малом, но конечном расстоянии друг от друга. Имелась возможность того, что обратная экспоненциальная функция расстояния (которую мы хотели бы видеть крайне малой), а не само расстояние, естественно оказалась бы небольшим числом. Если так, то предсказываемая иерархия между масштабом массы слабых взаимодействий и планковским масштабом масс была бы умеренным числом, а не (много меньшей) обратной экспонентой от этого числа, и наше решение не работало бы.
Гольдбергер и Вайс проделали важное исследование, закрывшее эту потенциально ненадежную дыру в теории, построенной Раманом и мной. Они показали, что расстояние между двумя бранами равно умеренному числу, а обратная экспонента от этого расстояния очень маленькая, в точности, как требовалось для того, чтобы наше решение работало.
Их идея была элегантна, и оказалось, что она имеет более общую применимость, чем кто-то мог в то время предположить. Выяснилось, что любая модель стабилизации очень похожа на их модель. Гольдбергер и Вайс предположили, что вдобавок к гравитону существует массивная частица, живущая в пятимерном балке. Они приписали этой частице свойства, которые позволили ей действовать, как пружине. В общем случае пружина имеет предпочтительную длину; пружина любой меньшей или большей длины будет переносить энергию, которая заставит пружину двигаться. Гольдбергер и Вайс ввели частицу (и связанное с ней поле), для которой равновесная конфигурация для поля и браны включала умеренное разделение бран, — опять же, то, что требовало наше решение проблемы иерархии.
Их решение базировалось на двух конкурирующих эффектах, один из которых предпочитал далеко разведенные браны, а другой — близко расположенные браны. Результатом была стабильная компромиссная позиция. Комбинация двух противодействующих эффектов естественно приводит к модели двух бран, в которой они находятся на умеренном расстоянии друг от друга.
Работа Гольдбергера — Вайса сделала ясным, что сценарий двух бран с закрученной геометрией действительно дает решение проблемы иерархии. И тот факт, что расстояние между бранами может быть фиксировано, было важным по другой причине. Если расстояние между бранами было неопределенным, браны могли двигаться рядом или разбегаться, если изменялась температура и энергия вселенной. Если расстояние между бранами могло изменяться, или если различные стороны пятимерной вселенной могли расширяться с разной скоростью, сама вселенная не эволюционировала так, как это предполагается в четырех измерениях. Так как астрофизики проверяли расширение Вселенной на поздней стадии ее эволюции, мы знаем, что недавно Вселенная расширялась так, как будто она была четырехмерной.
С учетом механизма стабилизации Гольдбергера — Вайса закрученная пятимерная вселенная согласуется с космологическими наблюдениями. Если браны стабилизированы по отношению к друг другу, вселенная будет эволюционировать так, как будто она четырехмерна, даже если на самом деле у нее пять измерений. Даже при наличии пятого измерения стабилизация будет жестко ограничивать различные положения вдоль пятого измерения, так чтобы они эволюционировали одинаково, и вселенная вела бы себя так, как будто она имеет четыре измерения. Так как стабилизация Гольдбергера — Вайса должна происходить сравнительно рано, закрученная вселенная будет выглядеть четырехмерной в течение большей части своей эволюции.
Как только стабилизация и космология стали понятными, в дело вошло решение проблемы иерархии с помощью закрученной геометрии. Скоро последовали многие другие интересные исследования, касающиеся этой закрученной геометрии. Одним из них было объединение взаимодействий. Все взаимодействия, включая гравитацию, могут быть объединены при высоких энергиях в закрученной геометрии, которую мы рассматриваем!
Закрученная геометрия и объединение взаимодействий
В гл. 13 объяснялось, почему главный козырь суперсимметрии — это то, что она может успешно обеспечить объединение взаимодействий. Теории с дополнительными измерениями, обращающиеся к проблеме иерархии, этого, кажется, лишены. Но так как мы не видели ни одного убедительного экспериментального свидетельства объединения — такого как распад протона — это не главная потеря, ибо мы не знаем до сих пор с уверенностью, что объединение правильно. Тем не менее три линии, сходящиеся в одной точке, выглядят интригующе и могут быть знамением чего-то важного. Даже если объединение еще не установлено достаточно твердо, мы не должны отвергать его слишком поспешно.
Алекс Помарол, испанский физик из Барселонского университета, заметил, что объединение взаимодействий может также происходить в закрученной геометрии. Однако схема, которую он рассматривал, слегка иная; электромагнитное, слабое и сильное взаимодействия не закреплены на бране, а вместо этого существуют в полном пятимерном балке. Калибровочные бозоны Стандартной модели — глюоны, W, Z и фотон — не прибиты к (три + одна) — мерной бране.
Согласно теории струн, калибровочные бозоны могут быть прибиты к бране с дополнительным числом измерений или, наряду с гравитацией, они могут находиться в балке. В противоположность гравитону, который должен возникать из замкнутой струны, калибровочные бозоны и заряженные фермионы могут соответствовать либо открытым, либо замкнутым струнам в зависимости от модели. Согласно тому, возникли ли они из открытых или замкнутых струн, калибровочные бозоны и фермионы будут либо прибиты к бране, либо получат возможность двигаться в балке.
В сценарии больших дополнительных измерений, если негравитационные взаимодействия находятся в балке, они оказываются слишком слабыми, чтобы согласовываться с наблюдениями. Взаимодействия в балке распространились бы по всему огромному пространству дополнительных измерений. Поэтому, как и в случае гравитации, они также будут очень сильно ослаблены. Это было бы неприемлемо, так как измеренные нами интенсивности взаимодействий оказались намного больше, чем эта теория может предсказать.
Но если дополнительные измерения не слишком велики, как в случае закрученной геометрии, не существует проблем с негравитационными взаимодействиями в пятимерном балке. Единственное, что их может ослабить, это не закручивание, а размер дополнительных измерений, но в закрученном сценарии этот размер довольно мал. Это означает, что истинная теория мира такова, что все четыре взаимодействия проявляются через балк. В этом случае не только частицы на бране, но и частицы во всем многомерном пространстве-времени могут ощущать электромагнитное, слабое и сильное взаимодействия, а также гравитацию.
Если калибровочные бозоны в закрученном сценарии присутствуют в балке, они могут иметь энергию, много большую чем ТэВ. Висящие в балке калибровочные бозоны будут ощущать весь диапазон энергий. Не чувствуя себя более привязанными к Слабой бране, они могут перемещаться везде в балке и обладать энергиями порядка планковского масштаба энергий. Только на Слабой бране энергия становится меньше, чем ТэВ. Так как взаимодействия находятся в балке и поэтому могут происходить при больших энергиях, становится возможным объединение взаимодействий. Это знаменательный факт, так как он означает, что взаимодействия могут объединяться при большой энергии даже в теории с дополнительными измерениями. Помарол получил очень интересный результат, что объединение действительно происходит почти так же, как будто теория является по-настоящему четырехмерной.
Но дела обстоят еще лучше. Объединение и механизм закрученной иерархии можно скомбинировать. Помарол показал, что взаимодействия объединяются, но он также предположил, что проблему иерархии решает суперсимметрия. Но для решения проблемы иерархии в закрученной геометрии требуется только, чтобы хиггсовская частица находилась на Слабой бране, так чтобы ее масса была близка к масштабу энергии слабых взаимодействий между 100 ГэВ и 1 ТэВ. Прибивать же калибровочные бозоны к бране не следует.

Все, что вам требуется в закрученной геометрии для решения проблемы иерархии, это малая величина массы хиггсовской частицы. Это происходит потому, что хиггсовское поле ответственно за спонтанное нарушение симметрии, являющееся источником масс всех элементарных частиц. Если симметрия слабого взаимодействия не будет нарушена, калибровочные бозоны и фермионы не будут иметь массы. До тех пор пока хиггсовская частица имеет масштаб массы слабых взаимодействий, массы слабых калибровочных бозонов оказываются правильными. Решение проблемы иерархии с помощью закрученной гравитации требует, в действительности, только одного — чтобы хиггсовская частица была на Слабой бране.
Все это означает, что если хиггсовская частица находится на Слабой бране, а кварки, лептоны и калибровочные бозоны — в балке (рис. 83), вы можете легко и просто получить желаемый результат. Слабая шкала будет защищена и будет иметь величину порядка ТэВ, но объединение сможет все же произойти при очень больших энергиях, на масштабе ТВО. Мой бывший студент Мэтью Шварц и я показали, что суперсимметрия не является единственной теорией, которая может быть согласована с объединением, — теория закрученных дополнительных измерений тоже может!
Экспериментальные приложения
Естественная шкала на Слабой бране порядка ТэВ. Если сценарий закрученной геометрии окажется правильным описанием нашего мира, его экспериментальные следствия на Большом адронном коллайдере в ЦЕРНе, Швейцария, будут потрясающими. Опознавательные знаки закрученного пятимерного пространства-времени могут включать частицы Калуцы — Клейна (КК), пятимерные черные дыры анти-де-ситтеровского пространства и струны ТэВной массы.
Частицы КК закрученного пространства-времени, вероятно, будут самыми доступными экспериментальными провозвестниками этой геометрии. Как всегда, частицы КК — это частицы, обладающие импульсом в дополнительных измерениях. Но новая загвоздка в этой модели состоит в том, что так как пространство искривленное, а не плоское, массы частиц КК будут отражать характерные особенности закрученной геометрии.
Так как единственная частица, про которую мы твердо знаем, что она распространяется в балке, это четырехмерный гравитон, сосредоточимся на его КК-партнерах. Как и в плоском пространстве, легчайшей из КК-партнеров гравитона будет частица, вообще не имеющая импульса в четвертом измерении. Такая частица будет неотличима от частицы подлинно четырехмерного происхождения: это гравитон, который будет переносить гравитацию в том, что выглядит как четырехмерный мир, и это гравитон, функцию вероятности которого мы детально изучали в этой главе. Если бы не было дополнительных частиц КК, гравитационное взаимодействие вело бы себя в точности так же, как в истинно четырехмерной вселенной. В этом сценарии вселенная по секрету пятимерна, но частица, которая действует как четырехмерный гравитон, не разоблачает этого факта. В отсутствие более тяжелых частиц КК мир Афины действительно кажется ей четырехмерным.
Только более массивные частицы КК могут рассказать о секретах пятимерной теории. Однако они должны быть достаточно легкими, чтобы рождаться. Вычисление значений масс частиц КК в этой теории довольно хитроумное. Из-за определенной геометрии частицы КК не будут обладать массами, пропорциональными обратным размерам измерения, как это было в случае свернутых измерений в плоском пространстве. Масса, пропорциональная обратному размеру, была бы чрезвычайно удивительной, так как для малых дополнительных измерений, которые мы рассматриваем, это должен быть планковский масштаб масс. На Слабой бране не может существовать ничего, что тяжелее чем ТэВ; никто, безусловно, никогда не нашел бы на ней объекта планковского масштаба масс.
Так как ТэВ — это масса, связанная со Слабой браной, вы не должны удивляться, что проведя аккуратно вычисления с учетом закрученного пространства-времени, масса частиц КК окажется порядка ТэВ. Если пятое измерение, как мы и предполагали, заканчивается на Слабой бране, то массы самых легких частиц КК и разность масс последовательно более тяжелых частиц КК оказываются порядка ТэВ. Частицы КК собираются на Слабой бране (поскольку их функция вероятности имеет там максимум), и обладают всеми свойствами частиц Слабой браны.
Это означает, что существуют КК-партнеры гравитона с массами порядка 1 ТэВ, 2 ТэВ, 3 ТэВ… В зависимости от окончательной энергии, которой достигнет БАК, есть хороший шанс найти одну или несколько из них. В противоположность КК-партнерам в сценарии больших дополнительных измерений, эти КК-партнеры взаимодействуют намного сильнее, чем гравитация.
Интенсивность взаимодействия этих частиц КК близко не приближается к интенсивности взаимодействия гравитона в четырех измерениях, — частицы КК обладают на 16 порядков величины большей интенсивностью взаимодействия. КК-партнеры гравитона взаимодействуют в нашей теории настолько

сильно, что любой КК-партнер, образованный на коллайдере, не будет просто исчезать из вида, унося энергию, не оставляя при этом никакого видимого сигнала. Напротив, КК-партнеры будут распадаться внутри детектора на детектируемые частицы, возможно, мюоны и электроны, которые можно использовать для реконструкции той частицы КК, от которой они произошли (рис. 84).
Это общепринятый рецепт открытия новых частиц: изучи все продукты распада и установи свойства той частицы, от которой они произошли. Если то, что вы нашли, не есть что-то, о чем вы знаете, это должно быть что-то новое. Если частицы КК распадаются в детекторе, сигнал от дополнительных измерений должен быть очень чистым. В нашей модели реконструкция масс и спинов частиц КК должна быть чрезвычайно полезными способом, который скорее сообщит нам о свойствах новых частиц, чем просто недостающая энергия, не имеющая никаких специальных меток о ее происхождении, позволяющих отличить эту модель от других. Значение спина частиц КК, равного 2, было бы действительным идентификационным знаком, который сообщил бы нам, что новые частицы имеют отношение к гравитации. Обнаружение частицы спина 2 и массы порядка ТэВ было бы необычайно сильным свидетельством в пользу закрученных дополнительных измерений. Несколько других моделей предсказывают существование таких тяжелых частиц спина 2, но с другими отличительными свойствами.
Если нам повезет, вдобавок к КК-партнерам гравитона эксперименты могли бы породить еще богатое множество частиц КК. В теории, согласно которой большинство частиц Стандартной модели находится в балке, мы могли бы увидеть также заряженные КК-партнеры кварков, лептонов и калибровочных бозонов. Эти частицы были бы заряженными и тяжелыми. И в конечном итоге они могли бы дать нам еще больше информации о многомерном мире.[161] На самом деле моделестроители Чаба Чаки, Кристоф Грожан, Луиджи Пило и Джон Тернинг показали, что в закрученном пространстве-времени с дополнительными измерениями и частицами Стандартной модели в балке электрослабая симметрия могла бы быть нарушена даже без хиггсовской частицы, а заряженные частицы, которые при этом могли бы обнаружить экспериментаторы, могли бы сообщить нам, является ли такая альтернативная модель верной для мира, в котором мы живем.
Еще более причудливая возможность
Я уже описывала несколько странных свойств дополнительных измерений. Но самая странная возможность еще впереди. Вскоре мы увидим, что закрученное дополнительное измерение может на самом деле простираться бесконечно далеко, оставаясь при этом ненаблюдаемым, в противоположность плоскому измерению, которое всегда должно иметь конечный размер, чтобы согласовываться с наблюдениями.
Этот результат поистине шокирует. В гл. 22, где мы обсудим это бесконечное дополнительное измерение, мы сосредоточимся на геометрии пространства, а не на проблеме иерархии. Но я кратко остановлюсь здесь на том, как можно решить проблему иерархии в случае пространства с бесконечным дополнительным измерением.
До сих пор мы рассматривали модель с двумя бранами: Гравитационной браной и Слабой браной, причем обе они ограничивали пятое измерение. Однако Слабая брана не обязана быть концом мира (т. е. границей пятого измерения). Если хиггсовская частица закреплена на второй бране, расположенной в середине бесконечного дополнительного измерения, то такая модель также может решить проблему иерархии. Функция вероятности гравитона была бы очень малой на Слабой бране, гравитация была бы слабой, и проблема иерархии решалась бы как и раньше, когда Слабая брана ограничивала пятое измерение. Функция вероятности гравитона в модели с бесконечным закрученным измерением продолжалась бы за пределы Слабой браны, но это не повлияло бы на решение проблемы иерархии, которое основано только на малости функции вероятности гравитона на Слабой бране.
Однако, поскольку измерение бесконечно, частицы КК имели бы другие массы и взаимодействия, так что экспериментальные следствия этой модели отличались бы от тех, которые я только что описала. Когда мы с Джо Ликкеном впервые обсуждали эту возможность в Аспеновском физическом центре (вдохновляющее место, а также одна из причин, по которым многие физики-теоретики любят гулять пешком), мы не были уверены, будет ли эта идея на самом деле работать. Если бы пятое измерение не кончалось на Слабой бране, не все частицы КК были бы тяжелыми (и имели бы массу порядка ТэВ). Массы некоторых частиц КК были бы крохотными. Если бы эти частицы были обнаружимы, но экспериментаторы до сих пор их не открыли, модель должна была бы быть исключена.
Но оказалось, что модель выжила. Сидя на скамейке, окруженная роскошным горным пейзажем, я решала задачу о взаимодействиях частиц КК (Джо занимался такими же вычислениями, но, я полагаю, он находился в своем кабинете в Центре). Мы получили результат, из которого следовало, что хотя взаимодействия частиц КК были достаточно велики, чтобы представлять интерес для будущих экспериментов, они были недостаточно велики для того, чтобы их уже можно было наблюдать.
В будущем БАК дает хороший шанс рождать частицы КК этой модели, если они существуют. Такие частицы будут выглядеть не так, как частицы из моделей с конечными закрученными дополнительными измерениями. Вместо милых частиц КК, распадающихся внутри детектора, частицы КК в модели с бесконечным дополнительным измерением сбегут в дополнительное измерение (похоже на поведение частиц КК, когда имеются большие измерения). Поэтому, если существует бесконечное закрученное дополнительное измерение и Слабая брана, решающая проблему иерархии, экспериментаторы могут только надеяться обнаружить события с недостающей энергией. Даже в этом случае при достаточно больших энергиях недостающая энергия должна быть достаточно ясным сигналом того, что где-то здесь есть нечто новое.
Черные дыры, струны и другие сюрпризы
Когда запустят БАК, то вдобавок к частицам КК могут появиться и другие примечательные сигналы дополнительных измерений. Хотя эффекты пятимерной гравитации при обычных энергиях ничтожно малы, но когда коллайдер начнет рождать частицы больших энергий, пятимерная гравитация станет главным игроком. На самом деле, когда энергии достигнут примерно ТэВ, эффекты пятимерной гравитации станут огромными, они перекроют взаимодействия слабо взаимодействующего четырехмерного гравитона, имеющего очень малую функцию вероятности на Слабой бране, где мы живем (и ставятся эксперименты).
Огромная интенсивность пятимерной гравитации означает, что могут рождаться пятимерные черные дыры, а также пятимерные струны. Кроме того, как только энергии достигнут величины порядка ТэВ, все, что сосредоточено на Слабой бране или в ее окрестности, будет сильно взаимодействовать со всем остальным. Это произойдет потому, что эффекты гравитации и дополнительных частиц КК будут огромными при ТэВных энергиях, и они будут сговариваться, чтобы все взаимодействовало со всем. Такие сильные взаимодействия между всеми известными частицами и гравитацией не возникают в четырехмерном сценарии; это будет ясный сигнал о чем-то новом. Как и в случае больших дополнительных измерений, мы до сих пор не знаем, хватит ли энергии, чтобы увидеть эти новые объекты. Но если взаимодействия сильны при энергиях, не слишком превышающих ТэВ, эксперименты этого не пропустят.
Кода
Связь между решением проблемы иерархии и экспериментальными следствиями при ТэВных энергиях очень крепка, но детали того, что мы увидим, зависят от модели. Разные модели приводят к различным экспериментальным следствиям, и это обнадеживает. Эти определенные опознавательные знаки означают, что как только запустят БАК, у нас появится хороший шанс установить, какая из этих моделей (если это имеет место) применима к нашему миру.
Что нового
• Пространство-время может быть сильно искривлено вследствие присутствия энергии в балке и бране, даже если сама брана совершенно плоская.
• Рассмотренная в этой главе модель имеет две браны, Гравитационную и Слабую, на каждом из концов пятого измерения конечных размеров. Энергия в балке и на бранах закручивает пространство-время.
• Единственное дополнительное измерение предлагает совершенно новый способ решения проблемы иерархии. Пятое измерение в этой модели невелико, но очень закручено. Интенсивность гравитации сильно зависит от того, где вы находитесь в пятом измерении. Гравитация сильна на Гравитационной бране и очень слаба на Слабой бране, где живем мы с вами.
• С точки зрения наблюдателя, считающего, что он находится в четырех измерениях, объекты могут иметь разные размеры и массы, если они берут начало в разных местах в пятом измерении. Объекты, прикрепленные к Гравитационной бране, должны быть очень тяжелыми (с массой порядка планковского масштаба масс), в то время как объекты, прикрепленные к Слабой бране, должны иметь значительно меньшие массы порядка ТэВ.
• Все взаимодействия могут объединиться, и проблема иерархии может быть решена, если хиггсовская частица (но не калибровочные бозоны) прикреплена к Слабой бране.
• Калуца-клейновские партнеры гравитона на коллайдере должны приводить к очень отчетливым событиям, в которых они распадаются на частицы Стандартной модели внутри детектора.
• В моделях, в которых частицы Стандартной модели находятся в балке, могут рождаться и распадаться и другие частицы КК.
Глава 21
Закрученная аннотированная «Алиса»[162]
Go ask Alice.
When she’s ten feet tall.
Jefferson Airplane[163]
Сказочный лифт остановился в закрученном пятимерном мире. Афина вышла из лифта и очень удивилась, увидев только три пространственных измерения. Неужто Кролик подшутил над ней? он говорил, что приведет ее в мир с четырьмя пространственными измерениями, но на самом деле их там было только три! И зачем путешествовать по миру, который выглядит как обычный?![164]
Местный житель с большой любезностью принял озадаченную гостью. «Приветствую Вас в Брансвилле[165], нашей славной столице. Разрешите мне помочь Вам осмотреться». Афина, усталая и озадаченная, тут же выпалила: «Брансвилл совсем не выглядит как-то особенно. Даже мэр выглядит совершенно нормально», хотя она могла поклясться, что не была в этом уверена, так как никогда раньше не видела мэра.
Мэр, к которому обратилась Афина, появился в сопровождении своего Главного Советника, Чеширского Толстого Кота. Обязанность Кота заключалась в том, чтобы следить за всем происходящим в городе, и она сильно облегчалась его способностью захватывать жителей врасплох, что было особенно удивительно с учетом невероятной величины Кота, кот обожал объяснять, что он обязан своим мастерством способности прятаться в балке, но никто даже не понимал, что он имел в виду[166].
Кот материализовался рядом с Афиной и спросил, не хочет ли она сопровождать его, пока он совершает свой обход. Он предупредил, что ей придется освоиться с невероятными размерами, но Афина его заверила, что ее любимый дядя был, на самом деле, очень, очень толстым, кот отнесся к этому скептически, но согласился взять ее с собой. Он предложил Афине сливочное пирожное с масляной глазурью, которое она с удовольствием съела. И они пустились в путь.
Афин а заинтересовалась, что же она съела. Ей сейчас казалось, что она находится на четырехмерном срезе пятимерного мира, и, насколько она могла судить, она была не толще, чем этот тонкий четырехмерный срез, она воскликнула: «Я сейчас выгляжу, как моя бумажная кукла! Но в то время как Долли имеет два пространственных измерения в трехмерном мире, у меня три пространственных измерения в четырехмерном пространственном мире».
Кот глубокомысленно ухмыльнулся и объяснил: «Вы сейчас ощущаете то, что я предпочитаю называть Балком. Вы все еще находитесь в Брансвилле, но через мгновение покинете его (и вырастите), в действительности Брансвилл есть часть пятимерной вселенной, но пятое измерение закручивается так осторожно, что жители Брансвилла совершенно не чувствуют его существования. У них нет даже представления о том, что Брансвилл есть граница пятимерного штата, вы также ошибочно заключили при своем появлении, что существуют только три пространственных измерения. Новая Афина, не привязанная к бране, свободно может перемещаться в пятом измерении, могу ли я предложить в качестве места назначения другую деревню, находящуюся на другом краю пятимерной вселенной и называемую Слабой браной?»

Какое странное оказалось пятимерное путешествие, покинув Брансвилл, Афина оказалась движущейся в другом измерении и растущей, как это уже с ней бывало (см. рис. 85).[167] Внимательный Кот заметил смущение на лице Афины и обнадеживающе объяснил: «Слабая брана уже близко, и мы там скоро будем[168]. Там красиво, но не волнуйтесь, когда вы увидите, что, как и жители Брансвилла, с которыми вы уже сталкивались, жители слабой браны издеваются над понятием четырех пространственных измерений, вы, имея возможность видеть через балк, увидите огромную тень над Брансвиллом, в десять миллионов миллиардов раз больше, чем та, с которой вы начинали. Почти все остальное будет казаться вам и им совершенно нормальным».
Но по прибытии на слабую брану Афина заметила еще одну вещь, путешественников на их пути спокойно сопровождал четырехмерный гравитон, который мягко трогал ее за плечо, он касался ее настолько нежно, что она едва могла это заметить[169].
Но Афина не могла продолжать игнорировать гравитон, ибо он пустился в долгое перечисление жалоб. «Слабая брана была бы такой замечательной, если бы не превосходящее влияние укоренившейся иерархии. Сильные, слабые и электромагнитные вооруженные силы на Слабой бране позволяют мне оказывать только самое слабое сопротивление». Гравитон жаловался, что в любом другом месте он был бы силой, с которой считаются, особенно в Брансвилле, управлявшемся олигархами, обладавшими сравнительно большими вооруженными силами[170]. Слабая брана, на которой гравитация была подавлена сильнее всего, была самым нелюбимым местом гравитона [171]. Гравитон обратился к Афине с надеждой поддержать его план выбить власть из рук правящей элиты.
Афина подумала, что ей лучше немедленно вернуться, и оглянулась в поисках кроличьей норы, но не смогла найти ее. Но она заметила белого кролика, и посчитала, что он будет хорошим гидом, но кролик слабой браны был поразительно медлителен, и продолжал все время повторять, как он счастлив, что почти не стареет[172]. Афина поняла, что этот кролик никуда не годится, и нашла более шустрого кролика, за которым она последовала и совершила обратный путь домой. Афина получила большое удовольствие от своего сна, как только поняла его физический смысл, хотя следует заметить, что она никогда больше не ела сливочных пирожных.
Глава 22
Глубокий пассаж: бесконечное дополнительное измерение
From, another dimension,
With voyeuristic intention,
Let’s do the Time Warp again.
Vanessa («The Rocky Horror Picture Show»)[173]
Афина вздрогнула и проснулась. Ее повторяющийся сон вновь провел ее вниз по норе Кролика. Однако на этот раз она попросила Кролика проводить ее прямо в закрученный пятимерный мир.
Афина опять вернулась в Брансвилл (или ей так казалось), вскоре появился Кот, и она с нетерпением повернулась к нему, предвкушая пирожное и замечательную экскурсию на Слабую брану. Она была горько разочарована, когда Кот сказал ей, что здесь, в этой конкретной вселенной, нет такой вещи, как Слабая брана[174].
Афина не поверила коту и подумала, что где-то дальше должна быть другая брана. Гордая собой за понимание того, каким образом в закрученной геометрии более далекие браны обладают более слабой гравитацией, она решила, что такую брану можно назвать Послушной браной, и с просила Кота, может ли она попасть туда.
Но снова она была вне себя от разочарования, кот объяснил: «Такого места нет. вы находитесь на Бране; других бран не существует». «Все страньше и страньше», — подумала Афина. Очевидно, что это не было точно то же место, что и раньше, так как имелась только одна брана, но Афин а была не готова сдаваться. «Могу я сама убедиться, что другой браны не существует?» — спросила она самым нежным голоском.
Кот решительно предостерег против этого, предупредив, что «четырехмерная гравитация на Бране не гарантирует четырехмерной гравитации в балке, однажды я потерял там почти все, кроме своей улыбки», несмотря на множество приключений, Афина была осмотрительной девочкой, и она приняла предупреждение Кота близко к сердцу, но она часто задавалась вопросом, что же имел в виду Кот. Что находится за браной, и как об этом можно узнать?
Искривленное пространство-время обладает удивительными свойствами. В гл. 20 мы использовали некоторые из них, включая то, как масса, размер и интенсивность гравитации могут зависеть от местоположения. В этой главе мы обсудим еще более удивительные свойства искривленного пространства-времени: оно может казаться четырехмерным, хотя на самом деле оно пятимерно. Исследуя закрученную геометрию пространства-времени более внимательно, мы с Раманом, к своему удивлению, осознали, что даже бесконечное дополнительное измерение может иногда быть невидимым.
Геометрия пространства-времени, которую мы рассмотрим в этой главе, практически совпадает с рассмотренной в гл. 20.

Однако, как рассказано в истории перед началом этой главы, такая геометрия обладает единственным отличительным свойством: она имеет только одну брану. Но это невероятно важное различие: так как нет второй граничной браны, наличие единственной браны означает, что пятое измерение бесконечно (рис. 86).
Это громадное различие. Через три четверти века после того, как в 1919 году Теодор Калуца предложил идею дополнительного измерения пространства, физики поверили, что дополнительные измерения приемлемы, но только если они имеют конечный размер, и либо свернуты, либо ограничены между бранами. Считалось, что бесконечные дополнительные измерения очень легко исключить, так как гравитационное взаимодействие, которое распространилось бы бесконечно далеко в этих измерениях, выглядело бы неправильно на всех масштабах расстояний, даже на тех, про которые мы уже знаем. Предполагалось, что бесконечное пятое измерение дестабилизирует все вокруг нас, даже Солнечную систему, которая удерживается в равновесии благодаря ньютоновской физике.
В этой главе объясняется, почему такое рассуждение не всегда правильно. Мы обсудим обнаруженное Раманом и мной в 1999 году совершенно новое соображение о том, почему дополнительные измерения могут быть скрытыми. Пространство-время может быть настолько закручено, что гравитационное поле сильно концентрируется в малой области вблизи браны, причем концентрируется настолько, что огромная протяженность бесконечного измерения становится несущественной. Гравитационное взаимодействие не теряется в дополнительных измерениях, а остается сфокусированным в малой области вблизи браны.
В этом сценарии гравитон, частица, переносящая гравитацию, локализован вблизи браны, которая и есть Брана из истории Афины, но с этого момента я буду называть ее Гравитационной браной. Афина во сне попала в это закрученное пятимерное пространство, в котором Гравитационная брана столь радикально изменяет природу пространства-времени, что пространство кажется четырехмерным, хотя оно в действительности пятимерное. Примечательно, что закрученное более высокое измерение может иметь бесконечную протяженность, но тем не менее быть скрытым, в то время как три плоских бесконечных измерения воспроизводят физику нашего мира.
Локализованная гравитация
Вспомним, что когда я впервые вводила понятие браны, я подчеркивала разницу между нежеланием путешествовать далеко от дома и настоящим заточением, когда явно запрещается покидать пределы той области, где что-то или кто-то находится в заключении. Возможно, вы никогда не бывали в Гренландии, но никакие законы не запрещают этого. Однако посещение некоторых мест сопряжено с большими хлопотами. Даже если путешествие в такие места разрешено, и даже если эти места находятся немногим дальше других мест, где вы бывали, вы все же можете никогда туда не попасть.
Или вообразите, что кто-то сломал ногу. В принципе, этот человек мог бы выходить из дома, когда захочет, но значительно вероятнее, что он будет находиться внутри дома больше времени, чем снаружи, даже когда никакие засовы и ключи не удерживают его внутри.
Аналогично, локализованный гравитон имеет неограниченный доступ в бесконечное пятое измерение. Тем не менее он сильно сконцентрирован в окрестности браны и имеет очень малую вероятность обнаружиться где-то вдали. Согласно общей теории относительности, все, включая гравитон, подвержено действию гравитационной силы. У гравитона нет никаких ограничений, но он ведет себя так, как будто он гравитационно притянут к бране и поэтому остается близко от нее. А поскольку гравитон очень редко выходит за пределы ограниченной области, дополнительное измерение может быть бесконечным, не порождая никаких опасных эффектов, которые закрыли бы такую теорию.
В нашей работе Раман и я сконцентрировались на гравитации в пятимерном пространстве-времени с одним единственным дополнительным измерением пространства. Мы могли поэтому сконцентрироваться на механизме локализации, который мы сейчас обсудим, и который удерживает гравитацию в малой области пятимерного пространства-времени. Я буду предполагать, что если вселенная имеет десять или более измерений, существует некоторая комбинация локализации и скручивания, которая прячет остальные. Такие дополнительные скрытые измерения не будут влиять на явление локализации, так что мы проигнорируем эти измерения и сфокусируем внимание на пяти измерениях, критически важных для нашего обсуждения.
В нашей модели единственная брана находится на одном конце пятого пространственно-временного измерения. Она отражающая, как и две браны, описанные мной в гл. 20. Предметы, которые ударяются о брану, просто отскакивают назад, так что не происходит потери энергии. Так как модель, которую мы сейчас рассматриваем, содержит только одну эту брану, мы предположим, что частицы Стандартной модели удерживаются на ней; обратим внимание на отличие от модели, обсуждавшейся в предыдущей главе, где частицы Стандартной модели были на Слабой бране, которой теперь больше не существует. Местонахождение частиц Стандартной модели не имеет отношения к геометрии пространства-времени, но оно, конечно, имеет следствия для физики частиц.
Хотя в этой главе нас интересует теория с одной браной, первым сигналом, что бесконечное пятое измерение может иметь право на жизнь, было любопытное свойство закрученной геометрии с двумя бранами. Мы сначала предполагали, что вторая брана выполняет две функции. Одна состояла в том, чтобы удержать частицы Стандартной модели; вторая заключалась в том, чтобы сделать пятое измерение конечным. Как и в случае плоских дополнительных измерений, конечное пятое измерение гарантировало, что на достаточно больших расстояниях гравитация будет такой же, как и в четырехмерном пространстве-времени.
Однако обнаружился любопытный факт, что последняя роль для второй браны была отвлекающим маневром и что вторая брана была несущественна для того, чтобы гравитация воспроизводила исходную гравитацию четырехмерной вселенной: взаимодействия четырехмерного гравитона были виртуально независимы от размера пятого измерения. Расчет показал, что гравитация будет иметь одинаковую интенсивность, если вторая брана будет находиться там, где она есть, или она будет в два раза дальше от Гравитационной браны, или если она будет в десять раз дальше внутри балка, все дальше и дальше от первой браны. На самом деле четырехмерная гравитация сохранится, даже если наша модель отодвинет вторую брану на бесконечность, иными словами, полностью ее устранит. Это не должно быть верно, если вторая брана и конечное измерение существенны для воспроизведения четырехмерной гравитации.
Это был наш первый ключ к пониманию того, что наше интуитивное желание иметь вторую брану было основано на плоских измерениях и не было обязательно верным в закрученном пространстве-времени. При плоском дополнительном измерении вторая брана обязательна для четырехмерной гравитации. Это можно увидеть с помощью аналогии с разбрызгивателем из гл. 20. Плоское дополнительное измерение будет соответствовать воде, распределяющейся везде одинаково вдоль длинного прямого шланга (рис. 81 на стр. 314)[175]. Чем длиннее разбрызгиватель, тем меньше воды будет попадать на каждый конкретный газон. Если распространить эти рассуждения на бесконечно длинный разбрызгиватель, мы увидим, что вода будет подаваться так скупо, что, по существу, на любой газон конечных размеров вода практически не будет попадать.
Аналогично, если гравитация распространялась бы через все бесконечное однородное измерение, гравитационная сила была бы настолько ослаблена вдоль бесконечного пятого измерения, что она свелась бы к нулю. В геометрии с бесконечным дополнительным измерением должна присутствовать некая тонкость, выходящая за рамки такой простой интуитивной картины, если гравитация должна вести себя четырехмерно. И действительно, закрученное пространство-время обеспечивает необходимый дополнительный штрих.
Чтобы увидеть, как это действует, еще раз используем аналогию с разбрызгивателем, чтобы выявить пробел в предыдущем рассуждении. Пусть у вас есть бесконечно длинный разбрызгиватель, но вы не подаете воду всюду в равных количествах. Вместо этого вы контролируете то, как распределена вода, чтобы убедиться, что ваш собственный участок хорошо полит. Один способ достичь этого — использовать половину воды для вашего участка, а остальную часть — за его пределами. В этом случае, хотя удаленные участки будут плохо политы, ваш участок гарантировано получит всю необходимую воду. Ваш участок всегда будет получать половину воды, даже если разбрызгиватель будет продолжать подавать воду на бесконечно далекое расстояние. При таком неравномерном распределении воды ваш участок будет получать всю необходимую воду. Разбрызгиватель мог быть бесконечным, но вы могли бы не знать расстояние.
Аналогично, функция вероятности гравитона в нашей закрученной геометрии всегда очень велика вблизи Гравитационной браны, несмотря на бесконечное пятое измерение. Как и в предыдущей главе, функция вероятности гравитона имеет максимум на этой бране (рис. 87), и экспоненциально падает, когда гравитон движется от гравитационной браны в пятое измерение. Однако в этой теории функция вероятности гравитона продолжается бесконечно далеко, но она несопоставима с величиной функции вероятности гравитона вблизи браны.

Быстро падающая функция вероятности такого типа показывает, что вероятность обнаружить гравитон вдали от Гравитационной браны необычайно мала, настолько мала, что мы можем в общем случае пренебречь удаленными областями пятого измерения. Хотя в принципе гравитон может находиться где угодно на пятом измерении, экспоненциальное убывание делает функцию вероятности гравитона сильно сконцентрированной в окрестности Гравитационной браны. Ситуация почти (но не совсем) такая, как будто вторая брана удерживает гравитон в ограниченной области.

Большую вероятность обнаружения гравитона вблизи Гравитационной браны и соответствующую концентрацию гравитационного поля в этой области можно сравнить с большой вероятностью нахождения прожорливых уток в пруду вблизи берега. Обычно утки не плавают равномерно по пруду, а концентрируются вблизи кусочков хлеба, которые им бросают любители птиц (рис. 88). Поэтому размер пруда будет совершенно несущественно влиять на распределение уток. Аналогично, в закрученном пространстве-времени гравитация притягивает гравитон к Гравитационной бране, так что протяженность пятого измерения несущественна.
Можно также увидеть, почему пятое измерение не влияет слишком сильно на гравитацию, рассмотрев гравитационное поле, окружающее тело на Гравитационной бране. Мы видели, что в плоских пространственных измерениях силовые линии, исходящие от тела, равномерно распределяются по всем направлениям. Когда существуют конечные дополнительные измерения, линии поля распространяются по всем направлениям до тех пор, пока какая-то из них не достигнет границы и не повернет назад. По этой причине линии гравитационного поля, находящиеся дальше от тела, чем размер дополнительных измерений, распространятся только по трем бесконечным измерениям мира с малой размерностью.


С другой стороны, в закрученном сценарии линии поля распределяются равномерно по всем направлениям, только находясь рядом с браной. В направлении, перпендикулярном бране, их очень мало (рис. 89). Так как линии гравитационного поля распространяются в основном вдоль браны, гравитационное поле выглядит почти тождественным полю, связанному с телом в четырех измерениях. Распространение в пятое измерение настолько мало (не больше, чем планковский масштаб длины 10-33 см), что мы можем его проигнорировать. Хотя дополнительное измерение бесконечно, оно несущественно для гравитационного поля связанного с браной тела.
Вы можете также понять, каким образом Раман и я разрешили исходную загадку, с которой мы столкнулись: почему размер пятого измерения несуществен для определения интенсивности гравитации. Возвращаясь к аналогии с разбрызгивателем, предположим, что мы задаем распределение воды по всему разбрызгивателю, так что оно напоминает распределение гравитации от резко падающей функции вероятности гравитона: после того как вы забираете половину воды для своего участка, вы отдаете половину оставшейся воды на соседний участок, половину этого количества — на следующий участок и т. д., причем каждый из последующих участков получает вдвое меньше воды, чем предыдущий. Чтобы имитировать вторую брану в пятом измерении, предположим, что мы прекращаем подачу воды после некоторой точки, точно так же, как вторая брана в пятом измерении обрезала бы функцию вероятности гравитона в некоторой точке вдоль пятого измерения. Для того чтобы представить бесконечное пятое измерение, предположим, что разбрызгиватель подает воду неограниченно вдоль своей длины.
Чтобы показать, что размер пятого измерения не имеет отношения к интенсивности гравитации вблизи браны, мы хотели бы показать, что первые несколько участков получают практически одинаковое количество воды, независимо от того, прекращаем ли мы подачу воды после того, как ее получит пятый участок, или десятый участок, или мы вообще не прекращаем подачу воды. Поэтому рассмотрим, что случится, если разбрызгиватель перекроют после первых пяти участков. Так как шестой и последующие участки будут получать очень мало воды, полное количество воды, которое разбрызгиватель будет подавать на несколько первых участков, будет отличаться от того количества, которое подаст бесконечный разбрызгиватель, лишь на несколько процентов. Если вы перекроете разбрызгиватель после седьмого участка, отличие станет еще меньше. При таком распределении, когда почти вся вода используется на полив нескольких первых участков, удаленные участки, получающие только малую долю воды, несущественны при оценке количества воды, попадающей на несколько первых участков[176].
Так как я хочу в следующей главе опять использовать аналогию с утками, я поясню то же самое с помощью подсчета уток, приплывших к берегу, когда кто-то бросает им куски хлеба. Если вы сначала сосчитаете ближайших уток, затем тех, которые подальше, продолжать подсчет скоро станет почти бесполезно. К моменту, когда вы охватите взглядом акваторию чуть дальше вглубь озера, останется очень мало уток, избежавших подсчета. Вам не нужно продолжать считать уток вдали от берега, так как вы уже сосчитали практически всех, ограничившись областью вблизи берега (рис. 88).
Функция вероятности гравитона просто так мала в области за второй браной, что местонахождение второй браны может привести только к пренебрежимо малой разнице в интенсивности взаимодействия четырехмерного гравитона. Иными словами, расстояние, на которое простирается пятое измерение, несущественно для проявляющейся интенсивности четырехмерной гравитации в этой теории, в которой гравитационное поле сосредоточено вблизи Гравитационной браны. Даже если бы не было второй браны и пятое измерение было бы бесконечным, гравитация продолжала бы выглядеть четырехмерной.
Мы с Раманом назвали наш сценарий локализованной гравитацией. Название выбрано так потому, что функция вероятности гравитона локализована вблизи браны. Хотя, строго говоря, гравитация может просачиваться в пятое измерение, так как это измерение действительно бесконечно, в реальности этого не происходит из-за малой вероятности обнаружения гравитона вдали от браны. Пространство не усечено, но все остается в концентрированной области в окрестности браны. Удаленная брана не приводит к изменению физических процессов на Гравитационной бране, так как мало что из Гравитационной браны рискует удалиться на большое расстояние. Все, что рождается на Гравитационной бране или вблизи нее, так и остается вблизи, в ограниченной области.
Иногда физики ссылаются на эту модель локализованной гравитации как на RS2. Здесь RS — это Рэндалл и Сундрум, но цифра 2 вводит в заблуждение. Она относится к тому факту, что это была вторая работа, которую мы написали по поводу закрученных измерений, но не к тому, что в работе были две браны. Сценарий с двумя бранами, посвященный проблеме иерархии, известен как RS1. (Названия приводили бы к меньшей путанице, если бы мы писали работы в обратном порядке.) В противоположность RS1, сценарий в этой главе не относится к проблеме иерархии, хотя вы можете ввести вторую брану и с тем же успехом решить эту проблему, как мы коротко рассмотрели в конце гл. 20. Но есть ли в пространстве вторая брана для решения проблемы иерархии или ее нет, локализованная гравитация есть радикальная возможность с важными теоретическими следствиями, идущими вразрез с устоявшимся предположением о том, что дополнительные измерения должны быть компактными.
Калуца-клейновские (КК) партнеры гравитона
В предыдущем разделе обсуждалась функция вероятности гравитона, которая была в большой степени сконцентрирована на Гравитационной бране. Частица, о которой я буду говорить, играет роль четырехмерного гравитона, так как она распространяется почти исключительно вдоль браны и обладает лишь крохотной вероятностью просочиться в пятое измерение. С точки зрения гравитона пространство выглядит так, как будто пятое измерение имеет не бесконечный размер, а размер порядка 10-33 см (размер, определяемый кривизной, которая, в свою очередь, определяется энергией в балке и на бране).
Но хотя Раман и я были довольно взволнованы своим открытием, мы не были уверены в том, что решили проблему до конца. Достаточно ли само по себе наличие локализованного гравитона, чтобы построить четырехмерную эффективную теорию, в которой гравитация ведет себя так, как будто она четырехмерна? Потенциальная проблема была в том, что калуца-клейновские партнеры гравитона могли бы также давать вклад в гравитационное взаимодействие и поэтому существенно модифицировать гравитацию.
Нас беспокоило то, что, вообще говоря, чем больше размер дополнительного измерения, тем меньше масса легчайшей частицы КК. Для нашей теории с бесконечным измерением это означало бы, что легчайшая частица КК могла бы быть произвольно легкой. Но так как разность масс частиц КК также уменьшается при увеличении размера дополнительного измерения, при любой конечной энергии может рождаться бесконечно большое количество типов очень легких КК-партнеров гравитона. Все эти частицы КК могли бы, в принципе, давать вклад в закон гравитационного взаимодействия и изменять его. Проблема выглядела особенно трудной, так как даже если каждая частица КК взаимодействовала бы очень слабо, если их было слишком много, то гравитационное взаимодействие выглядело бы тем не менее совершенно иначе, чем в четырех измерениях.
И главное, так как частицы КК чрезвычайно легкие, их можно легко рождать. Коллайдеры уже работают при энергиях, достаточных для рождения этих частиц. Даже обычные физические процессы, например химические реакции, порождают достаточно энергии, чтобы образовать КК-партнеров гравитона. Если бы частицы КК переносили много энергии в пятимерный балк, теория была бы неверной.
К счастью, оказывается, что ни одно из этих предположений не является проблемой. Когда мы рассчитывали функции вероятности для частиц КК, мы нашли, что КК-партнеры гравитона взаимодействуют очень слабо на Гравитационной бране или вблизи нее. Несмотря на большое число КК-партнеров гравитона, все они взаимодействуют столь слабо, что нет никакой опасности произвести слишком большое их количество, или где-то изменить форму гравитационного взаимодействия. Если и есть какая-то проблема, она состоит в том, что эта теория настолько близко имитирует четырехмерную гравитацию, что мы до сих пор не знаем способа экспериментально отличить ее от истинно четырехмерного мира! КК-партнеры гравитона будут вносить столь ничтожный вклад во все наблюдаемые эффекты, что мы до сих пор не знаем, как описать разницу между четырьмя плоскими измерениями и четырьмя плоскими измерениями, дополненными пятым закрученным измерением.
Слабость взаимодействий КК-партнеров гравитона можно понять, взглянув на форму их функций вероятности. Как и для гравитона, они указывают на вероятность, с какой любая частица может быть обнаруженны в любом положении вдоль пятого измерения. Раман и я следовали более или менее стандартной процедуре нахождения масс и функций вероятности каждого КК-партнера гравитона в нашей закрученной геометрии. Это включало решение квантово-механической задачи.
Для плоского пятого измерения описанная в гл. 6 квантово-механическая задача состояла в том, чтобы найти волны, которые укладываются на закрученном в кольцо измерении, и тем самым проквантовать разрешенные энергии[177]. Для нашей закрученной бесконечной пятимерной геометрии квантово-механическая проблемы выглядела несколько иначе, так как нам нужно было учесть энергию на бране и в балке, которые закручивали пространство-время. Но мы сумели модифицировать стандартную процедуру так, чтобы она походила для нашей схемы. Результаты оказались ошеломляющими.
Первая частица КК, которую мы нашли, была частицей без импульса в пятом измерении. Функция вероятности этой частицы была сильно сконцентрирована на Гравитационной бране и экспоненциально убывала вдали от нее. Эта форма выглядела знакомой: это была функция вероятности для того же четырехмерного гравитона, которую мы уже обсуждали. Такая безмассовая мода КК есть четырехмерный гравитон, переносящий ньютоновский четырехмерный закон тяготения.
Однако остающиеся частицы КК очень разные. Ни одна из них, похоже, не находится вблизи Гравитационной браны. Вместо этого, мы нашли, что для любого значения массы между нулем и планковским масштабом масс существуют частица КК с этой конкретной массой, и функция вероятности каждой из этих частиц имеет максимум в разных местах вдоль пятого измерения.
На самом деле существует интересная интерпретация локализации разных пиков. В гл. 20 мы видели, что для того, чтобы рассматривать все частицы на равном основании в четырехмерной эффективной теории в закрученном пространстве-времени, так чтобы все они одинаково взаимодействовали с гравитацией, мы по-разному изменяем масштаб всех расстояний, моментов времени, энергий и импульсов вдоль пятого измерения. При перемещении в сторону от браны, каждая точка ассоциируется с экспоненциально уменьшающейся энергией. Именно поэтому частицы на Слабой бране имеют массы порядка ТэВ. Тень путешествующей Афины из пятого измерения становится больше, а сама Афина становится легче, когда она движется от Гравитационной браны к Слабой бране.
Каждая точка вдоль пятого измерения может быть сопоставлена таким же образом с конкретной массой; масса связывается с планковским масштабом масс путем изменения масштаба в этой точке. Частица КК, функция гравитации которой имеет максимум в определенной точке, имеет приблизительно такую же изменившую масштаб массу. Когда вы перемещаетесь в пятом измерении, вы сталкиваетесь последовательно со все более легкими частицами КК в точках, где их функции вероятности достигают максимума.
На самом деле можно сказать, что спектр КК представляет крайне сегрегированное общество. Тяжелые частицы КК изгоняются из областей пространства, где изменившая масштаб энергия слишком мала, чтобы их образовать. Легкие частицы КК встречаются редко в тех областях, которые содержат частицы больших энергий. При заданной массе, частицы КК концентрируются как можно дальше от Слабой браны. Их положения напоминают то, как сидят модные штаны на подростках — настолько мешковато-большие, насколько это возможно, чтобы только не упасть. К счастью, законы физики, определяющие местоположение частиц КК, легче понять, чем подростковую моду.
Для нас самым важным свойством функций вероятности для легких частиц КК является то, что на Гравитационной бране они очень малы. Это означает, что есть только малая вероятность найти частицы КК вблизи этой браны или на ней. Поскольку легкие частицы КК как можно сильнее шарахаются от Гравитационной браны, легкие частицы (помимо гравитона, функция вероятности которого имеет максимум на Гравитационной бране) будут рождаться очень редко. Кроме того, легкие частицы КК несущественно модифицируют закон гравитационного взаимодействия, так как они имеют тенденцию держаться подальше от Гравитационной браны и поэтому слабо взаимодействуют с частицами, закрепленными на бране.
Собрав все это вместе, Раман и я решили, что нам удалось найти теорию, которая работает. Локализованный на Гравитационной бране гравитон ответствен за появление четырехмерной гравитации. Несмотря на большое количество КК-партнеров гравитона, они взаимодействуют так слабо на Гравитационной бране, что их проявления совершенно незаметны. И несмотря на существование бесконечного пятого измерения, все физические законы и процессы, включая гравитационные, кажется согласуются с тем, что ожидается в четырехмерном мире. В этом сильно закрученном пространстве допустимо бесконечное дополнительное измерение.
Как было ранее отмечено, с наблюдательной точки зрения такая модель несколько разочаровывает. Как ни удивительно может показаться, эта пятимерная модель так хорошо имитирует четыре измерения, что крайне тяжело разделить их. Экспериментаторов, занимающихся физикой частиц, безусловно, ждут тяжелые времена.
Однако физики начали исследовать астрофизические и космологические свойства, которые могли бы разделить два мира. Многие физики[178] рассматривали черные дыры в закрученном пространстве-времени, и продолжают исследовать, существуют ли отличительные свойства, которые мы могли бы использовать для определения того, во вселенной какого типа мы на самом деле живем.
В настоящее время мы знаем, что локализация — это новая и заманчивая теоретическая возможность для существования в нашей вселенной дополнительных измерений. Я страстно ожидаю дальнейших исследований, которые могли бы окончательно определить, является ли это истинным свойством нашего мира.
Что нового
• Измерение может быть бесконечно длинным, но невидимым, если пространство-время должным образом закручено.
• Гравитацию можно локализовать, даже если она не закреплена жестко в конечной области.
• В локализованной гравитации безмассовая частица КК есть локализованный гравитон. Он концентрируется вблизи Гравитационной браны.
• Все другие частицы КК концентрируются вдали от Гравитационной браны; форма их функции вероятности и положения, где эти функции достигают максимума, зависят от их массы.
Глава 23
Задумчивый и раздвигающий пассаж
Someday girl I don’t know when
We’re gonna get to that place
Where we really want to go.
Bruce Springsteen[179]
Икар XLII решил жить с размахом. Он нацелился испытать сверхвысокие настройки Алисэксвира на многие мегапарсеки, с помощью которых он мог бы выйти за пределы Галактики и известной вселенной и ощутить простор далеких областей, которых никто ранее не видел.
Икар был восхищен, когда Алисэксвир унес его вдаль на расстояния в 9, 12 и даже 13 миллиардов световых лет. но его восторг поутих, когда он попытался пойти еще дальше, ибо тут мощность его сигнала резко упала, когда он замахнулся на 15 миллиардов световых лет, его полет прервалось полностью: он больше не получал никакой информации. Вместо этого он услышал: «Сообщение 5В73: клиент на Горизонте, с которым вы пытаетесь связаться, находится все зоны действия сети. Если вам нужна помощь, пожалуйста, обратитесь к вашему оператору дальней связи».
Он не верил своим ушам. Это был тридцать первый век, и тем не менее его служба Горизонта все еще обеспечивала только ограниченное покрытие, когда Икар попытался обратиться к оператору, автоответчик сказал: «пожалуйста, оставайтесь на бране. Вы получите ответ в порядке очередности поступления вызова». Икар подозревал, что оператор не ответит никогда, и был достаточно мудр, чтобы не ждать.
Предыдущая глава объяснила, почему искривление может снять ограничения на дополнительное измерение и позволить ему быть бесконечным и тем не менее ненаблюдаемым. Но бесконечное дополнительное измерение не есть конец физического рассказа: вещи становятся еще более странными. В этой главе будет объяснено, как четырехмерная гравитация (т. е. с тремя пространственными измерениями и одним временным) может быть по-настоящему локальным явлением, — гравитация может выглядеть совсем иначе вдалеке. Мы увидим, что не только пространство-время может казаться четырехмерным, когда в действительности имеется пять измерений, но и что мы можем жить в изолированном кармане с четырехмерной гравитацией внутри пятимерной вселенной.
Модель, которую мы сейчас рассмотрим, показывает, что разные области пространства могут обладать разным числом измерений. В процессе исследования некоторых необычных свойств локализованной гравитации физик Андреас Карч и я нашли модель пространства-времени, в которой это действительно происходит. Новый радикальный сценарий, к которому мы пришли, предполагает, что причина, по которой мы не видим дополнительные измерения, может быть более странной, чем кто-либо мог предполагать. Мы можем жить в четырехмерной дыре, в которой наличие трех пространственных измерения является просто следствием случайного расположения.
Осмысление
Когда я вновь просматриваю электронную почту того времени, когда Раман и я работали вместе, меня удивляет, что мы сумели закончить нашу работу среди такого большого количества отвлекающих обстоятельств. Когда мы начали наши исследования, я была в процессе переезда из МИТ в Принстон, где должна была занять должность профессора, и я также занималась планированием шестимесячного визита в Санта-Барбару в следующем году. Раман, проведя несколько лет на пост-докторских позициях, переживал, удастся ли ему получить работу на факультете, поэтому занимался подготовкой соответствующих докладов и документов. В это было трудно поверить. Он сделал прекрасную работу, и я и другие пытались убедить его, что в конце концов все получится, и ему не следует оставлять физику и пытаться сделать другую карьеру. Раман был явно предназначен для физики и определенно заслуживал отличной должности на факультете, и тем не менее у него были проблемы с работой. Мейлы того времени демонстрируют хаос: интересные физические темы чередуются с просьбами о рекомендательных письмах, с назначением времени докладов, с поисками жилья в Принстоне и с организацией конференции в Санта-Барбаре. Также было несколько обменов мейлами с другими физиками по поводу нашей работы. Но немного. Хотя работа RS2 была в конечном счете процитирована тысячи раз и получила признание, ее первоначальное восприятие было смешанным. Прошло некоторое время, прежде чем большинство физиков поняли нас и поверили нам. Один коллега говорил мне, что люди ожидали, что выход найдет кто-то другой, и поэтому не обращали на работу внимания. Конечно, вряд ли можно сказать, что доклад Рамана в Принстоне был встречен с энтузиазмом.
Даже те, кто действительно слушали, не обязательно проникались сразу нашей идеей. Обсуждение с теоретиком-струнником Энди Стромингером прояснило очень много, и теперь он смеется над тем, как сначала не воспринял ни одного нашего слова. К счастью, он не был слишком скептически настроен для того, чтобы слушать и разговаривать.
В физическом сообществе были некоторые, кто понял и поверил в то, что мы сделали, с самого начала. Нам повезло, что среди них был Стивен Хокинг, и что он сразу поделился своим энтузиазмом с физической аудиторией. Я вспоминаю, что Раман возбужденно говорил мне, как на престижных лекциях Лёба в Гарварде Хокинг сконцентрировался, в основном, на нашей работе.
Несколько других физиков также работали над близкими проблемами. Но следующей осенью, через несколько месяцев после того, как наша работа была опубликована (и через много месяцев после того, как мы начали говорить о ней), все физическое сообщество начало обращать на нее внимание. Счастливым случаем оказалось то, что Давид Кутасов, израильский физик из Чикагского университета, Миша Шифман, физик-частичник русского происхождения из университета Миннесоты, и я организовали осенью 1999 года шестимесячный семинар в Институте теоретической физики Кавли в Санта-Барбаре. Первоначальной целью этого семинара было свести вместе теоретиков-струнников и строителей моделей и извлечь пользу из возникшего слияния интересов в исследованиях таких тем, как суперсимметрия и калибровочные теории сильных взаимодействий. Мы начали планировать семинар заранее, до того, как понятие бран и дополнительных измерений вмзвало такой ажиотаж.
Хотя мы надеялись на некоторое сотрудничество между теоретиками-струн-никами и строителями моделей, мы не знали в начале организации семинара, что мы будем думать о дополнительных измерениях, когда конференция действительно будет происходить.
Но время проведения оказалось счастливым. Семинар предоставил замечательную возможность облечь в плоть наши идеи о дополнительных измерениях, а для строителей моделей, специалистов по струнам и общей теории относительности — поделиться опытом. Произошло много восхитительных дискуссий, и закрученная геометрия была одной из главных тем. Наконец и строители моделей, и специалисты по струнам восприняли закрученную пятимерную геометрию всерьез. В действительности различие между двумя областями сгладилось, когда люди стали работать вместе над подобными проблемами закрученной геометрии и другими идеями.
В дальнейшем многие физики работали над другими аспектами закрученной геометрии, устанавливая связи и исследуя тонкости, что сделало локализованную гравитацию еще более интересной. Хотя специалисты по струнам сначала отметали RS1 (закрученную геометрию с двумя бранами) как модель, как только они начали исследования, они нашли способы реализовать сценарий RS1 в теории струн. Вопросы теории черных дыр, временной эволюции и связи с идеями из теории струн и частиц также оказались плодородной почвой для исследований. Локализованная гравитация теперь изучалась в различных контекстах, и новые идеи продолжают появляться.
После того как наша теория была принята, некоторые физики фактически ударились в другую крайность, заявляя, что в нашей теории нет ничего нового. Один специалист по струнам пошел настолько далеко, что заключил, что вычисление в теории струн влияния мод Калуцы — Клейна было «дымящимся револьвером», который доказывал, что наша теория была не чем иным, как версией теории струн, которую физики-струнники уже изучали. Это соответствует шутливой присказке в науке о том, что новая теория проходит через три фазы, прежде чем быть признанной: сначала она неправильная, затем очевидная и, наконец, кто-нибудь утверждает, что кто-то другой уже сделал это первым. В нашем случае, однако, «дымящийся револьвер» превратился в дым, когда физики осознали, что вычисления в теории струн были намного сложнее, чем они думали, и что желаемый ответ из теории струн в действительности был ошибочным. Правдой же было то, что пересечение с работами из теории струн было волнующим для всех нас и привело и к новым важным прозрениям. Оказалось, что локализованная гравитация сильно пересекалась с самыми важными идеями в развитии теории струн того времени: и наша работа, и исследования теоретиков-струнников привлекали аналогичную закрученную геометрию. В действительности, возможно потому, что наши исследования не бросали прямого вызова моделям теории струн, сообщество теории струн фактически приняло и признало важность нашей работы скорее, чем сообщество строителей моделей. Хотя сначала это казалось случайным, возможно, это было указание на то, что все мы были на правильном пути. И к счастью, у Рамана в дальнейшем больше не было проблем с трудоустройством (он теперь профессор в Университете Джона Хопкинса).
Однако некоторые скептики остаются. Точная модель, которую рассмотрели Раман и я, привела к интересным вопросам, на которые не было немедленного ответа. Зависела ли локализация от формы пространства-времени на больших расстояниях? Когда люди пытались найти примеры геометрии того типа, который предложили Раман и я, в теориях супергравитации, форма гравитации вдали от локализующей браны казалась непреодолимым препятствием. Но были ли эти условия важными? Другой вопрос, на который мы хотели ответить, был о том, везде ли пространство-время с необходимостью кажется четырехмерным? Локализованная гравитация заставила всю пятимерную вселенную вести себя так, как будто бы гравитация была четырехмерной. Всегда ли это так, или некоторые области могли казаться четырехмерными, а некоторые могли вести себя по-другому? И что происходит, когда брана неплоская? Работает ли локализация точно так же для браны с другой геометрией? Это некоторые из вопросов, на которые обращена теория локально локализованной гравитации, которую развили Андреас и я.
Локально локализованная гравитация
Так сколько же измерений у пространства? Действительно ли мы это знаем? Теперь, я надеюсь, вы согласитесь с тем, что было бы излишним заявлять, что мы наверняка знаем, что дополнительные измерения не существуют. Мы видим три пространственных измерения, но могут быть еще такие, которые мы пока не обнаружили.
Вы теперь знаете, что дополнительные измерения могут быть спрятанными или потому, что они свернуты и малы, или потому, что пространство-время искривлено и гравитация сконцентрирована в небольшой области, так что даже бесконечное измерение невидимо. В любом случае, компактны ли измерения или локализованы, пространство-время будет казаться четырехмерным везде, где бы вы ни были.
Это может быть немного менее очевидным в сценарии локализованной гравитации, в котором вероятностная функция гравитона становится все меньше и меньше по мере того, как вы идете в пятое измерение. Гравитация действует так же, как в четырех измерениях, если вы находитесь рядом с браной. Но как обстоят дела в других областях?
Ответ состоит в том, что в модели RS1 влияние четырехмерной гравитации неизбежно, где бы вы ни были в пятом измерении. Хотя вероятностная функция гравитона максимальна на бране, объекты повсюду могут взаимодействовать друг с другом посредством обмена гравитоном, и поэтому все объекты будут испытывать четырехмерную гравитацию независимо от места их локализации. Гравитация повсюду выглядит четырехмерной, потому что вероятностная функция гравитона никогда точно не равна нулю — она продолжается повсюду. В локализованном сценарии объекты вдали от браны имели бы крайне слабое гравитационное взаимодействие, но слабая гравитация, тем не менее, вела бы себя четырехмерным образом. Так, например, ньютоновский закон обратных квадратов все равно выполнялся бы, неважно, где вы находитесь в пятом измерении.
Маленькая, но ненулевая вероятностная функция гравитона вдали от браны была важна для решения проблемы иерархии, которое я изложила в гл. 20. Слабая брана, расположенная вдали от Гравибраны в балке, чувствует гравитацию, которая оказывается четырехмерной, даже если она чувствует ее крайне слабо. Как вода вдали от вашего участка в аналогии с разбрызгивателем — вода всегда есть, хотя ее и немного.
Но предположим, что мы размышляем далее и спрашиваем, что мы действительно точно знаем о размерностях пространства. Мы не знаем, что пространство повсюду кажется трехмерным, а только что пространство рядом с нами кажется трехмерным. Пространство представляется имеющим три измерения (а пространство-время — четыре) на расстояниях, которые мы можем видеть. Но пространство может простираться за эти пределы в недостижимую область.
В конце концов, скорость света конечна, и наша Вселенная существует только конечное время. Это значит, что мы можем знать только об окружающей нас области пространства в пределах того расстояния, которое свет прошел с момента рождения Вселенной. Это не бесконечно далеко. Это определяет область, известную как горизонт, разделительная линия между информацией, которая доступна и недоступна для нас. За горизонтом мы не знаем ничего. Революция, произведенная Коперником, постоянно обновляется и пересматривается по мере того, как мы вглядываемся все дальше во Вселенную и осознаем, что не везде все с необходимостью такое же, как то, что мы видим. Даже если законы физики везде одинаковы, это не значит, что сцена, на которой они действуют, везде такая же. Возможно, близкие браны индуцируют другой закон изменения гравитационной силы вокруг нас, чем тот, который наблюдается в других местах.
Как можем мы заявлять, что знаем размерность вселенной вне границ нашего видения? Не было бы никакого противоречия, если бы вселенная за их пределами являла собой больше измерений — может пять, может десять, а может и больше. Думая скорее о голых сущностях, чем предполагая, что повсюду, даже в недостижимых областях, пространство-время выглядит как наше, мы можем вывести, что действительно фундаментально, а что крайне постижимо и законно.
Все, что мы знаем, это то, что воспринимаемое нами пространство-время оказывается четырехмерным. Возможно, предполагая, что все остальные области вселенной также должны быть четырехмерными, мы переходим границу разумного. Почему мир, предельно далекий от нашего и, возможно, совсем не взаимодействующий с нами или же взаимодействующий посредством крайне слабых гравитационных сигналов, должен видеть гравитацию и пространство такими же, какими их видим мы? Почему в нем не может быть гравитация другого типа?
Замечательная вещь состоит в том, что это возможно. Наш мир на бране может воспринимать три плюс одно измерения, в то время как область вне его другая. К нашему крайнему удивлению, в 2000 году у нас с Андреасом Карчем родилась теория, в которой пространство-время выглядит четырехмерным на или вблизи браны, но большая часть пространства-времени вдали от браны оказывается многомерной. Эта идея схематически представлена на рис. 90.
Мы назвали наш сценарий локально локализованная гравитация, потому что локализация порождает гравитон, который передает четырехмерное гравитационное взаимодействие только в локальной области — остальное пространство-
время не выглядит четырехмерным. Четырехмерный мир[180] может существовать только на гравитационном «острове». Размерность пространства, которую вы наблюдаете, зависит от вашего положения в пятимерном балке.
Чтобы понять локальную локализацию, давайте вернемся к нашим уткам в пруду. Вы могли бы не согласиться, когда я сказала, что размер пруда не имеет значения. Если бы пруд был действительно огромный, утки на противоположной стороне не смогли бы присоединиться к уткам на вашей стороне. Действительно, было бы очень странным, если бы вы смогли влиять на уток, которые были очень далеко. Далекие утки не заметили бы ваш хлеб и плавали бы в удаленной части пруда.
Основная идея, заложенная в локально локализованную гравитацию, очень похожа на эту. Локализация гравитации на бране не должна с необходимостью зависеть от того, что происходит в удаленных областях пространства. Хотя в модели, которую я изучала с Раманом, был гравитон, вероятностная функция которого спадала экспоненциально, но нигде не обращалась в нуль — и эта четырехмерная гравитация должна была ощущаться везде — поведение гравитации на больших расстояниях не должно было быть существенным для определения того, существует ли четырехмерная гравитация в окрестности браны.
В этом суть локально локализованной гравитации. Гравитон может быть локализован и порождать четырехмерную гравитационную силу в окрестности браны, не влияя на гравитационную силу вдалеке. Четырехмерная гравитация может быть совершенно локальным феноменом, относящимся только к некоторой части пространства.
По иронии судьбы Андреас, замечательный физик и приятный парень, начал думать о модели, которая допускала такую возможность, когда занимался исследовательским проектом с одним из моих прежних коллег по МИТ, который намеревался оспорить мою работу с Раманом (к счастью для нас, в результате их сотрудничества появилась замечательная работа, показывающая, что наша работа правильна). По ходу работы над проектом, Андреас нашел модель, которая была очень близка к развитой Раманом и мной, но обладала некоторыми очень необычными свойствами. Когда Андреас был в Принстоне, он зашел ко мне поговорить об этом. Позже мы выяснили, что у этой модели были удивительные следствия. Сначала мы с Андреасом обсуждали результаты по электронной почте и во время посещений институтов друг друга, а впоследствии, когда я вернулась в Бостон, более просто. И то, что мы нашли, было воистину замечательно.
Эта модель была очень похожа на ту, которую я изучала с Раманом; в ней была одна брана в закрученном пятимерном пространстве. Но отличие в этом случае было в том, что брана не была точно плоская. Это было потому, что она имела очень малую отрицательную вакуумную плотность энергии. В общей теории относительности, как мы видели, не только относительная энергия, но и полное количество энергии имеет смысл. Полная энергия говорит пространству, как оно должно искривляться. Например, постоянная отрицательная плотность энергии в пятимерном пространстве-времени приводит в точности к тому искривленному пространству, которое мы обсуждали в нескольких последних главах. Однако в том случае сами браны были плоскими. Здесь же отрицательная плотность энергии на бране делает ее немного искривленной.
Отрицательная плотность энергии на бране приводит к даже более интересной теории. Мы, однако, не интересовались отрицательной плотностью энергии самой по себе — если мы живем на бране, наша брана в действительности должна иметь очень малую положительную плотность энергии для того, чтобы было согласие с экспериментальными наблюдениями. Андреас и я решили изучить эту модель только потому, что она приводила к зачаровывающим следствиям для размерности. Для понимания того, что мы нашли, давайте ненадолго вернемся к постановке задачи с двумя бранами, имея в виду, что впоследствии мы удалим вторую брану. Когда вторая брана находится достаточно далеко, мы обнаружили, что существует два разных гравитона, каждый из которых локализован около одной из бран. Каждая из вероятностных функций гравитонов имела максимум около соответствующей браны и экспоненциально спадала вдали от нее.
Ни один из гравитонов не отвечал за четырехмерную гравитацию во всем пространстве. Они порождали четырехмерную гравитацию только в областях, прилегающих к бранам, на которых они локализованы. Гравитационные взаимодействия, ощущаемые на разных бранах, были различными. Они даже могли иметь существенно разные силы. И объекты на одной бране не взаимодействовали гравитационно с объектами на другой бране. Ситуацию с двумя широко разделенными бранами можно сравнить с ситуацией, когда кто-то на противоположном, очень далеком берегу тоже кормит уток. Те утки могли бы быть совершенно другого типа; возможно, вы зовете крякв, но на другом берегу кто-то зовет лесных уток. В этом случае у другого берега будет второе скопление уток, аналогичное вероятностной функции гравитона, который локализован у второй браны.
Появление двух различных частиц, выглядящих как четырехмерный гравитон, было для нас большим сюрпризом. Предполагалось, что общие физические принципы обеспечивают существование только одной теории гравитации. И конечно, пятимерная теория гравитации единственна. Однако оказывается, что пятимерное пространство содержит две разных частицы, каждая из которых передает гравитационную силу, представляющуюся четырехмерной, но каждая из которых действует в разных областях пятимерного пространства. Различные области пятимерного пространства выглядят так, как будто в них действует четырехмерная гравитация, но гравитоны, переносящие гравитационную силу в этих областях, оказываются разными.
Но был еще и второй сюрприз. В соответствии с общей теорией относительности гравитон безмассовый. Подобно фотону, он должен двигаться со скоростью света. Но Андреас и я обнаружили, что один из гравитонов имеет ненулевую массу и не движется с этой скоростью. Это было действительно удивительно — но также и тревожно. В физической литературе говорится, что массивный гравитон не может порождать гравитационную силу, которая согласуется со всеми наблюдениями. В действительности, точно так же, как и в случае тяжелого калибровочного бозона в гл. 10, массивный гравитон будет иметь больше поляризаций, чем безмассовый. А физики показали, сравнивая различные измеренные гравитационные эффекты, что никаких эффектов от дополнительных поляризаций гравитона никогда замечено не было. Это озадачило нас на некоторое время.
Но наша модель оказалась остроумнее, чем обычная мудрость! Когда мы открыли эту модель, Массимо Поррати, физик из университета Нью-Йорка, Ян Коган, Ставрос Мусопулос и Антониос Папазуглу в Оксфордском университете нашли, что в некоторых случаях гравитон может иметь массу и, тем не менее, давать правильные гравитационные предсказания. Они проанализировали технические детали в теории и нашли прокол в той логике, согласно которой массивный гравитон не может согласовываться с наблюдаемыми гравитационными процессами.
А у модели были даже еще более необычные следствия. Давайте теперь подумаем о том, что случится, когда мы устраним вторую брану. Физические законы тогда по-прежнему будут казаться четырехмерными на оставшейся бране, на Гравибране, несмотря на бесконечное дополнительное измерение. Гравитация вблизи Гравибраны будет практически идентична гравитации в модели RS2. Для тел на Гравибране единственный гравитон передает гравитационную силу, и гравитация оказывается четырехмерной.
Однако между этой моделью и RS2 есть существенное различие. В этой модели, которая отличается только наличием отрицательной плотности энергии на бране, гравитон, который локализован на бране, не доминирует в гравитационном взаимодействии во всем пятимерном пространстве. Этот гравитон не взаимодействует с объектами повсюду; он порождает четырехмерную гравитацию только на бране или рядом с ней. Вдали от браны гравитация больше не кажется четырехмерной! ^
Может показаться, что это противоречит тому, что я говорила раньше, что гравитация должна существовать везде в пространстве дополнительных измерений. Это не ошибочное заявление; пятимерная гравитация существует везде. Однако, в отличие от других теорий с дополнительными измерениями, которые мы рассматривали до сих пор и в которых физика всегда имеет четырехмерную интерпретацию, эта теория выглядит четырехмерной только для объектов на бране или рядом с ней. И закон Ньютона для гравитационной силы тоже относится только к бране и области рядом с ней. Повсюду вне их гравитационная сила пятимерна. В такой постановке четырехмерная гравитация представляется совершенно локальным феноменом, воспринимаемым только в окрестности браны. Размерность пространства, которую вы выведете из поведения гравитации, будет зависеть от того, где вы находитесь в пятом измерении. Если эта модель правильна, мы должны жить на бране, чтобы ощущать четырехмерную гравитацию. Если бы мы были где-либо еще, гравитация выглядела бы пятимерной. Брана представляет собой четырехмерную гравитационную дыру — четырехмерный гравитационный остров.
Конечно, мы пока не знаем, имеет ли локально локализованная гравитация отношение к реальному миру. Мы не знаем даже, существуют ли дополнительные измерения, или, если они существуют, что с ними стало. Но если теория струн права, дополнительные измерения есть. Они могут быть скрыты или компактификацией, или локализацией (или локальной локализацией), или какой-либо комбинацией этих двух возможностей. Многие специалисты по теории струн продолжают верить, что ответ дает компактификация, но поскольку в теории гравитации, которая получается из теории струн, так много загадок, уверенным быть нельзя. Я рассматриваю локализацию как новый выбор. Когда гравитация локализована, физические законы таковы, как если бы дополнительных измерений не было, в точности так же, как со свернутыми измерениями. Поэтому локализованная гравитация дополняет наш инструментарий для построения моделей и повышает шансы открыть реализацию теории струн, которая согласовывается с экспериментом. Мне нравится то, что локально локализованная гравитация концентрируется на том, что мы действительно можем проверить. Она говорит только, что вселенная должна выглядеть четырехмерной там, где мы можем это проверить — а не то, что она должна быть четырехмерной. Наши три пространственных измерения могут быть просто случайным следствием нашего расположения. Эта идея пока еще не была полностью изучена. Но вполне оправдан вопрос о том, что различные области пространства могли бы иметь разное число измерений. В конце концов, новая физика открывается всякий раз, когда мы зондируем более короткие расстояния за пределами того, что мы уже видели раньше. Возможно, то же самое справедливо и для больших расстояний: если мы живем на бране, то кто знает, что находится вне ее?
Что нового
• Локализованная гравитация представляет собой локальный феномен. Она не зависит от удаленных областей пространства-времени.
• Гравитация может вести себя так, как если бы мир имел разное число измерений в разных областях, поскольку локализованный гравитон не обязательно простирается во всем пространстве.
• Мы можем жить в изолированном кармане пространства, который кажется четырехмерным.
VI Завершающие мысли
Глава 24
Дополнительные измерения: мы внутри или снаружи?
But I still haven’t found what I’m looking for.
U2[181]
Сказания о снах Афины о 1D-ленде, бранах и пяти измерениях передавались из поколения в поколение. Когда Икар XLll их услышал, он захотел проверить, была ли в этих рассказах доля истины. Поэтому он завел свой Алисэксвир и задал очень малый масштаб — не настолько малый, чтобы появились струны, но достаточно малый, чтобы проверить, есть ли пятое измерение. Алисэксвир послушно подчинился и привез Икара в пятимерный мир.
Но Икар не был полностью удовлетворен. Он помнил необычные вещи, которые случились раньше, когда он баловался с опциями гиперпривода. Поэтому он опять повернул рычаг гиперпривода — и опять все бешено переменилось. Икар не мог узнать ни одного привычного объекта. Он мог сказать только одно: пятое измерение исчезло.
Икар был в замешательстве. Поэтому он запросил в Спейснете информацию об «измерениях». Он побродил по многочисленным сайтам, отбрасывая кучу надоедливого спама, но скоро понял, что ему нужно уточнить критерии поиска. Когда же он снова не смог найти ничего определенного, он признал, что в ближайшее время узнать фундаментальную причину возникновения измерений не удастся. Поэтому Икар решил переключиться на путешествия во времени.
Физика вступила в замечательную эру. Идеи, которые когда-то были в царстве научной фантастики, входят в сферу нашей теоретической — и, возможно, даже экспериментальной — достижимости. Новейшие теоретические открытия о дополнительных измерениях необратимо изменили представление физиков-частичников, астрофизиков и космологов о нашем мире. Само количество и темп открытий говорят нам, что мы, вероятно, только дотронулись до крышки сокровищницы. Идеи обрели свою собственную жизнь.
Тем не менее нужно еще до конца ответить на многие вопросы, и наше путешествие еще далеко от завершения. Физики-частичники по-прежнему хотят знать, почему мы видим именно эти силы, и есть ли еще другие? Откуда берется масса и свойства близких частиц? Мы также хотим знать, верна ли теория струн. И если да, то как она связана с нашим миром?
Недавние космические наблюдения подбросили еще больше загадок, которыми мы хотим заняться. Из чего состоит большая часть энергии и вещества во Вселенной? Была ли короткая фаза взрывного расширения на ранней стадии эволюции Вселенной, и если да, то что ее вызвало? И каждый хочет знать, какой была Вселенная, когда она только начиналась.
Мы теперь знаем, что гравитация может вести себя очень по-разному на различных масштабах длины. На очень малых расстояниях только квантовая теория гравитации, такая как теория струн, будет описывать это взаимодействие. На больших масштабах общая теория относительности работает удивительно хорошо, но современные наблюдения Вселенной на очень больших расстояниях ставят космологическую загадку о том, что ускоряет ее расширение. А на еще больших расстояниях мы достигаем космологического горизонта, за которым мы вообще ничего не знаем.
Одним из интригующих аспектов теорий с дополнительными измерениями является то, что они естественным образом дают разные следствия на разных масштабах. Проявление гравитации в таких теориях на расстояниях меньших, чем свернутые измерения, или там, где кривизна слишком мала для того, чтобы оказывать влияние, отличается от ее поведения на больших расстояниях, где дополнительные измерения могут быть невидимы, или где искривление становится важным. Это дает нам основания думать, что дополнительные измерения могли бы когда-нибудь пролить свет на некоторые таинственные черты космоса. Если мы действительно живем в многомерном мире, мы, конечно же, не можем пренебрегать космологическими следствиями этого. Некоторые исследования в этой области уже были сделаны, но я уверена, что нас ожидает еще много интересных результатов.
Куда, на мой взгляд, физика пойдет дальше? Есть слишком много возможностей, для того чтобы их перечислять. Но позвольте мне описать несколько интригующих наблюдений, которые подсказывают, что еще много важных теоретических сюрпризов остается в запасе — тех, которые могут приблизиться к ответу в ближайшее время. Все эти тайны сконцентрированы вокруг вопроса, который в этом месте может показаться шокирующим, а именно:
Что же вообще такое измерения?
Как я могу задавать такой вопрос так поздно? Ведь я уже посвятила большую часть этой книги обсуждению дополнительных измерений и некоторым возможным следствиям предложенных миров с такими измерениями. Но теперь, когда я рассказала вам, что мы понимаем об измерениях, позвольте мне ненадолго вернуться к этому вопросу.
Так что же в действительности означает число измерений? Мы знаем, что число измерений определяется как число величин, необходимых для задания положения точки в пространстве. Но в гл. 15 и 16 я привела примеры, показывающие, что десятимерные теории иногда имеют те же физические следствия, что и одиннадцатимерные.
Такая дуальность подсказывает, что наше понятие измерения не настолько определенно, как кажется, — в определении есть пластичность, которая ускользает от обычной терминологии. Дуальные описания одной теории говорят нам, что ни одна из формулировок не является с необходимостью лучшей. Формулировки и даже число измерений в наилучшем описании могут зависеть, например, от величины струнной константы связи. Поскольку ни одна из теорий не дает лучшего описания, вопрос о числе измерений не всегда имеет простой ответ. Эта неопределенность в смысле измерений и явное появление дополнительного измерения в сильно взаимодействующих теориях представляют собой наиболее важные наблюдения в теоретической физике в последнее десятилетие. Позвольте мне теперь перечислить несколько наиболее интригующих теоретических открытий, которые указывают на то, что понятие измерения несколько более размыто, чем нам бы хотелось думать.
I. Закрученная геометрия и дуальность
В гл. 20 и 21 я объяснила некоторые следствия закрученной геометрии пространства-времени, которую предложили Раман Сундрум и я. В этой геометрии массы и размеры объектов зависят от расположения в пятом измерении, и еще гравитация локализована в окрестности браны. Но есть еще одна замечательная черта у этого закрученного пространства-времени, известного также как пространство анти-де Ситтера, о которой я теперь должна вам рассказать, — черта, которая порождает дальнейшие вопросы о размерности.
Эта замечательная черта пространства анти-де Ситтера заключается в существовании дуальной четырехмерной теории. Ход теоретических мыслей говорит нам, что все, что происходит в пятимерном пространстве анти-де Ситтера, может быть описано в рамках дуальной четырехмерной теории, в которой присутствуют крайне сильные взаимодействия с особыми свойствами. В соответствии с этой таинственной дуальностью все в пятимерной теории имеет аналог в четырехмерной теории. И наоборот.
Хотя математические рассуждения и говорят нам, что пятимерная теория в пространстве анти-де Ситтера эквивалента некоторой четырехмерной, мы не всегда знаем точный набор частиц в этой четырехмерной дуальной теории. Но в 1997 Хуан Малдасена, специалист по струнам (родом из Аргентины, сейчас в Принстоне), представил явный пример такой дуальности в этой теории, чем вызвал лихорадочную активность в теории струн. Он осознал, что версия теории струн с большим числом перекрывающихся Х) — бран, на которых струны сильно взаимодействуют, может быть описана или как четырехмерная квантовая теория поля, или как десятимерная теория гравитации, в которой пять из десяти измерений свернуты, а остальные пять образуют пространство анти-де Ситтера. Как мотут четырехмерная теория и пяти- или десятимерная теория иметь одинаковые следствия? Например, что есть аналог объекта, движущегося в пятом измерении? Ответ состоит в том, что объект, движущийся в пятом измерении, представляется в дуальной четырехмерной теории как объект, который растет или сжимается. Это в точности похоже на тень Афины на Гравибране, которая росла по мере того, как она уходила от Гравибраны через пятое измерение. Кроме того, объекты, движущиеся мимо друг друга в пятом измерении, соответствуют объектам, которые и растут, и сжимаются, и перекрываются в четырех измерениях.
Как только вы вводите браны, следствия дуальности становятся еще более странными. Например, пятимерное пространство анти-де Ситтера с гравитацией, но без бран эквивалентно четырехмерной теории без гравитации. Но как только вы включите в пятимерную теорию брану, как сделали мы с Раманом, эквивалентная четырехмерная теория неожиданно содержит гравитацию. Означает ли эта дуальность, что я вводила вас в заблуждение, когда говорила, что закрученные геометрии являются многомерными теориями? Абсолютно нет. Дуальность интригует, но в действительности она ничего не меняет в том, что я вам рассказала. Даже если кто-нибудь найдет точную дуальную четырехмерную теорию, такую теорию будет крайне трудно изучать. Она должна содержать огромное число частиц и такие крайне сильные взаимодействия, что теория возмущений (см. гл. 15) будет к ней неприменима.
Теории, в которых объекты взаимодействуют с большой силой, почти никогда не поддаются интерпретации без альтернативного описания со слабым взаимодействием. И в этом случае таким разумным описанием является пятимерная теория. Только пятимерная теория допускает достаточно простую подходящую для вычислений формулировку, поэтому имеет смысл думать о теории в пятимерных терминах. Тем не менее, даже если пятимерная теория проще для работы, дуальность все равно заставляет меня интересоваться тем, что же в действительности значит слово «измерения». Мы знаем, что число измерений должно быть числом величин, необходимых для того, чтобы задать положение объекта. Но всегда ли мы уверены в том, что мы знаем, какие величины нужно считать?
II. T-дуальность
Еще одной причиной задать вопрос о значении понятия измерения является эквивалентность между двумя внешне разными геометриями, известная как Т-дуальность. Еще до того, как физики открыли дуальности, которые я обсуждала, они уже открыли Т-дуальность, которая заменяет пространство с крошечным свернутым измерением на другое пространство с огромным свернутым измерением. Как это ни странно, в теории струн крайне малые и крайне большие свернутые измерения приводят к тем же физическим следствиям. Крошечный объем свернутого пространства приводит к тем же физическим следствиям, что и крайне большой.
Т-дуальность применима в теории струн со свернутыми измерениями, потому что в пространстве-времени, компактифицированном в окружность, есть два разных типа замкнутых струн, и эти два типа взаимозаменяются, когда пространство с малым свернутым измерением заменяется на пространство с большим свернутым измерением. Первый тип замкнутых струн осциллирует, когда он движется в свернутом измерении подобно калуца-клейновским частицам, которые мы рассматривали в гл. 18. Другой тип наматывается на свернутое измерение. Он может сделать это раз, два, или любое число раз. И операции Т-дуальности, которые заменяют малое свернутое измерение на большое, взаимозаменяют эти два типа струн.
В действительности Т-дуальность была первым указанием на то, что браны должны существовать: без них в дуальной теории не было бы аналога открытых струн. Но если T-дуальность применима, и крошечное свернутое измерение дает те же физические следствия, что и огромное свернутое измерение, это могло бы означать, что, опять же, наше понятие «измерения» неадекватно.
Это так потому, что если вы захотите сделать радиус одного свернутого измерения бесконечно большим, Т-дуальное свернутое измерение будет окружностью нулевого размера — т. е. окружности вообще не будет. То есть бесконечное измерение в одной теории T-дуально теории, в которой на одно измерение меньше (поскольку окружность нулевого размера не считается измерением). Так T-дуальность тоже показывает, что два внешне разных пространства могут казаться имеющими разное число больших протяженных измерений и тем не менее приводить к тождественным физическим предсказаниям. Еще раз повторю, что понятие измерения неоднозначно.
III. Зеркальная симметрия
T-дуальность применима, когда измерение свернуто в окружность. Но еще более необычная симметрия, чем T-дуальность, есть зеркальная симметрия, которая иногда используется в теории струн, если шесть измерений свернуты в многообразие Калаби — Яу. Зеркальная симметрия говорит, что шесть измерений могут быть свернуты в два очень разных многообразия Калаби — Яу, и тем не менее получающаяся четырехмерная теория на больших расстояниях может быть одной и той же. Многообразие, получающееся в результате применения этой зеркальной симметрии к некоторому многообразию Калаби — Яу, может выглядеть совершенно иначе: оно может иметь другую форму, размер, скрученность или даже некоторое число дырок[182]. Тем не менее, если для некоторого многообразия Калаби — Яу существует зеркальное, то физическая теория, где шесть измерений свернуты в одно из двух многообразий, будет одна и та же. Поэтому и с зеркальными многообразиями две явно разных геометрии приводят к тем же самым предсказаниям.
IV. Матричная теория
Матричная теория, инструмент для изучения теории струн, дает еще более таинственные подсказки про измерения. Поверхностно, матричная теория выглядит как квантово-механическая теория, которая описывает поведение и взаимодействия D0-бран (точечноподобных бран), движущихся в десяти измерениях. Но хотя теория явно не содержит гравитацию, D0-браны действуют как гравитоны. Так что в конце теория получается содержащей гравитационное взаимодействие, хотя гравитон внешне отсутствует.
Кроме того, теория D0-бран напоминает супергравитацию в одиннадцати измерениях, а не в десяти. То есть матричная модель выглядит так, как если бы она содержала супергравитацию в пространстве с размерностью на единицу больше, чем в исходной теории. Эта подсказка (наряду с другими математическими свидетельствами) привела теоретиков-струнников к убеждению, что матричная теория эквивалентна М-теории, которая также содержит одиннадцатимерную супергравитацию.
Одна особенно странная черта матричной теории была замечена Эдвардом Виттеном и состоит в том, что когда D0-браны подходят слишком близко друг к другу, нельзя точно знать, где они находятся. Как сказали Том Бэнкс, Уилли Фишлер, Стив Шенкер и Ленни Сасскинд — создатели матричной теории — «таким образом, для малых расстояний не существует представления конфигурационного пространства и терминах обычного положения»[183]. То есть положение D0-браны больше не является имеющей смысл математической величиной, когда вы пытаетесь определить его слишком точно.
Такие странные свойства делают матричную теорию мучительно трудной для изучения, и в настоящее время очень трудно использовать ее для вычислений. Проблема состоит в том, что, подобно другим теориям, содержащим сильно взаимодействующие объекты, никто еще не нашел способа решить многие важнейшие вопросы, которые помогут нам понять, что же в ней действительно происходит. Все же, из-за возникновения дополнительного измерения и исчезновения измерений, когда D0-браны подходят слишком близко друг к другу, матричная теория дает еще один повод думать о том, что же в действительности значат измерения.
О чем думать?
Хотя физики математически продемонстрировали эти таинственные эквивалентности между теориями с разным числом измерений, нам явно все еще не хватает полной картины. Знаем ли мы наверняка, что эти дуальности применимы, и если так, то что они говорят нам о природе пространства и времени? Более того, никто не знает, что будет лучшим описанием, когда измерение не слишком велико и не слишком мало (по сравнению с чрезвычайно малым планковским масштабом длины). Возможно, наше понятие пространства-времени просто полностью разваливается, как только мы пытаемся описать что-нибудь столь малое.
Одной из сильнейших причин для веры в то, что наше пространственно-временное описание неадекватно на планковском масштабе длины, является отсутствие даже теоретического метода исследования таких малых расстояний. Мы знаем из квантовой механики, что для исследования таких малых масштабов длины требуется огромная энергия. Но как только вы поместите слишком много энергии в область планковского размера, 10-33 см, вы получите черную дыру. И тогда у вас нет способа узнать, что же происходит внутри. Вся эта информация заключена внутри горизонта событий черной дыры.
Сверх того, даже если бы вы попытались впихнуть больше энергии в эту крошечную область, вам бы это не удалось. Как только вы закачаете так много энергии в область планковского размера, вы не сможете добавить еще, не расширяя эту область. То есть черная дыра будет расти, если вы добавляете энергию. Поэтому вместо того, чтобы получить хороший крошечный зонд для исследования таких расстояний, вы раздуете область до большего размера и никогда не сможете изучать ее, пока она маленькая. Это примерно то же, что изучать мелкие артефакты в музее с помощью тонкого лазерного луча — он их просто сожжет. Даже в мысленном физическом эксперименте вы попросту никогда не видите область, которая меньше планковского масштаба длины. Законы физики, которые мы знаем, нарушатся прежде, чем мы туда попадем. Где-то вблизи планковского масштаба длины привычные понятия пространства-времени почти наверняка неприменимы.
Столь странные факты требуют более глубокого объяснения. Одним из наиболее важных уроков невероятных открытий последнего десятилетия является то, что у пространства и времени есть более фундаментальные описания. Эд Виттен кратко обрисовал проблему емкой фразой «может оказаться, что пространство и время обречены». Многие ведущие специалисты по теории струн согласны с этим: Натан Зайберг утверждает: «Я почти уверен в том, что пространство и время — это иллюзии»; в то же время Дэвид Гросс полагает, что «очень вероятно, пространство и, возможно, даже время из чего-то составлены; пространство и время могут оказаться выводимыми свойствами некоторой теории, выглядящей совершенно иначе»[184]. К сожалению, пока никто не знает, какова может быть природа этого более фундаментального описания пространства-времени. Но бесспорно, что более глубокое понимание фундаментальной природы пространства и времени остается одним из самых масштабных вызовов для физиков в грядущие годы.
Глава 25
Открытое заключение
It’s the end of the world as we know к (and I feel fine).
REM[185]
Икар Раш мор XLII воспользовался машиной времени, чтобы посетить прошлое и предупредить Икара III о катастрофе, которая постигнет его, если он будет продолжать гонять на своем порше. Икар III был настолько поражен своим гостем из будущего, что внял доводам Икара XLII. Он поменял свой порше на фиат, и перешел к более спокойной жизни.
Афина была в восторге от того, что она вновь встретилась со своим братом, а Дитер был счастлив снова увидеть своего друга, хотя оба чувствовали себя неловко, так как казалось, что Икар никуда не отлучался. Афина и Дитер осознавали, что путешествие во времени, о котором рассказал Икар, было чистой фантазией. Даже в снах Кот никогда не замыкал петель во времени, кролик никогда не останавливал лифт на конце дополнительных временных измерений, и квантовый детектив отказывался считать вероятным такое странное поведение времени. Но Афина и Дитер предпочитали счастливые концы, поэтому они отложили недоверие и все-таки приняли фантастическую историю Икара.
Несмотря на впечатляющие достижения в физике за последние несколько лет, мы до сих пор не знаем, как использовать гравитационное взаимодействие или телепортировать объекты сквозь пространство, так что, возможно, еще несколько преждевременно инвестировать в собственность в дополнительных измерениях. И так как мы не знаем, как связать вселенные, в которых вы могли бы совершить переход сквозь время, с той вселенной, в которой мы живем, никто не может создать машину времени, и, вероятнее всего, никто не сможет сделать это в обозримом будущем (или прошлом).
Но даже если подобные идеи остаются в области научной фантастики, мы живем в прекрасном мире, полном загадок. Наша цель состоит в том, чтобы изучить, как его кусочки собираются в цельную картину и как они эволюционировали в теперешнее состояние. Что это за связи, которые мы еще не поняли? В чем состоят ответы на вопросы, подобные тем, что я задавала в конце последней главы?
Даже если нам еще предстоит понять окончательную структуру материи на глубочайшем уровне, я надеюсь, что убедила вас, что мы уже понимаем многие стороны ее фундаментальной природы на тех пространственных масштабах, которые мы экспериментально изучили. И даже если мы не знаем самые основные элементы пространства-времени, мы понимаем его свойства на расстояниях вдали от планковского масштаба длины. В таких режимах мы можем применять физические принципы, которые нам известны, и вывести ряд следствий, которые я описала. Мы столкнулись с большим количеством неожиданных свойств дополнительных измерений и бран, и эти свойства могут играть решающую роль при анализе многих загадок нашей вселенной. Сейчас мы знаем, что многомерные структуры могут проявляться в любом количестве форм и размеров. Они могут иметь закрученные дополнительные измерения или большие дополнительные измерения; они могут содержать одну брану или две; они могут содержать частицы в балке и другие частицы, прикрепленные к бранам. Космос может быть больше, богаче и разнообразнее, чем все, что мы можем представить.
Какая же из этих идей описывает реальный мир? Мы должны подождать, чтобы ответ дал реальный мир. Фантастично то, что это, вероятно, произойдет. Одно из самых волнующих свойств некоторых многомерных моделей, описанных в книге, это то, что у них есть экспериментальные следствия. Важность этого факта нельзя переоценить. Многомерные модели, с новыми свойствами, про которые мы думали, что они либо невозможны, либо скрыты, могут иметь следствия, которые можно наблюдать. И из этих следствий мы имеем возможность вывести существование дополнительных измерений. Если нам это удастся, наше представление о вселенной безвозвратно изменится.
Проверки теорий многомерного пространства-времени возможны и в астрофизике и космологии. Физики сейчас разрабатывают детальные теории черных дыр в многомерных мирах, и они нашли, что хотя их свойства по многом аналогичны свойствам черных дыр в четырех измерениях, имеются тонкие различия. Свойства многомерных черных дыр могут оказаться достаточно характерными, так что мы можем распознать отличительные черты.
Космологические наблюдения могли бы в конце концов больше сказать нам о структуре пространства-времени. Современные наблюдения говорят, как выглядела Вселенная миллиарды лет назад. Многие соглашаются с предсказаниями, но остается ряд важных вопросов. Если мы живем в многомерной Вселенной, она должна была раньше очень сильно отличаться от того, что есть сейчас, причем эти отличия могли бы помочь объяснить поразительные свойства, наблюдаемые в эксперименте. Сейчас физики изучают влияние дополнительных измерений на космологию. Нам потребуется узнать о черной материи, спрятанной на других бранах, или космологической энергии, запасенной в спрятанных многомерных объектах.
Но одно бесспорно. В течение следующих пяти лет будет запущен Большой адронный коллайдер (БАК) в ЦЕРНе [186], и он начнет исследовать физические области, которые до это были недоступны для наблюдения. Мои коллеги и я с нетерпением ожидаем наступления этого времени. БАК — это большая ставка, для ученых лучше не придумаешь. Эксперименты на БАК почти наверняка откроют частицы, свойства которых дадут нам новое понимание физики за рамками Стандартной модели. И очень возбуждает, что никто не знает, что за частицы будут открыты.
За все время, что я занимаюсь физикой, были открыты только такие новые частицы, существование которых с большой долей вероятности следовало из теоретических соображений. Ни в коей мере не умаляя важность этих открытий — среди них были очень впечатляющие достижения, следует сказать, что обнаружение чего-то фундаментально нового и неизвестного будет значительно более волнующим. Пока БАК не начнет работу, никто не может сказать с уверенностью, где следует концентрировать усилия. Результаты, полученные на БАК, похожи на смену нашего взгляда на мир.
БАК будет иметь достаточно большую энергию, чтобы порождать новые типы частиц, которые обещают снять завесу с многих тайн. Эти частицы могут оказаться суперпартнерами или другими частицами, которые предсказываются четырехмерными моделями. Но они могут оказаться частицами Калуцы— Клейна, которые путешествуют по дополнительным измерениям. Увидим ли мы эти частицы КК и когда это произойдет, полностью зависит от размера и формы космоса, в котором мы живем. Живем ли мы в многомерной вселенной? И будут ли размер и форма этой вселенной способствовать тому, чтобы частицы КК стали видимыми?
Все модели, предлагающие решение проблемы иерархии, имеют наблюдаемые следствия на масштабе энергий слабых взаимодействий. Особенно поразительны характерные следы закрученной геометрии, также дающей решение проблемы иерархии. Если эта теория верна, мы обнаружим частицы КК и измерим их свойства по оставленным ими за собой следам. Напротив, если Вселенную описывают другие многомерные модели, энергия будет исчезать в дополнительных измерениях, и мы в конечном итоге их обнаружим, детектируя нехватку энергии.
Безусловно, мы пока что не знаем всех ответов. Но Вселенная близка к тому, чтобы приоткрыть свои тайны. Астрофизические исследования обратятся к более ранним стадиям космоса, более далеким регионам и с большей детализацией, чем когда-либо ранее. Открытия на БАК расскажут нам о природе материи на расстояниях, меньше тех, на которых когда-либо изучались любые физические процессы. При больших энергиях начнется извержение новых знаний о Вселенной.
Секреты космоса начинают раскрываться. Что касается меня, я жду этого с нетерпением.
Глоссарий
Альфа-частица. Ядро атома гелия (состоит из двух протонов и двух нейтронов).
Анархический принцип. Утверждение, что все взаимодействия, которые не запрещены симметриями, будут происходить.
Аномалия. Нарушение симметрии, возникающее от квантовых вкладов в физическое взаимодействие, но отсутствующее в соответствующей классической теории (в которой квантовые поправки не принимаются во внимание).
Аномальная передача. Передача нарушения суперсимметрии квантовыми эффектами.
Античастица. Частица той же массы, что и другая частица, но противоположно заряженная.
Антропный принцип. Рассуждения, утверждающие, что из всех возможных вселенных мы можем жить лишь в тех, где может сформироваться структура.
Аромат. Метка, различающая разные типы кварков или лептонов (часто используется для различения кварков и лептонов из разных поколений).
Атом. Строительный блок материи, состоящий из электронов, вращающихся вокруг положительно заряженных ядер.
БАК (Большой адронный коллайдер). Ускоритель частиц высокой энергии, в котором сталкиваются встречные пучки протонов энергией 7 ТэВ, образуя частицы массой до нескольких ТэВ.
Балк. Полное многомерное пространство.
Бета-распад. Радиоактивный распад, в котором нейтрон превращается в протон, электрон и нейтрино.
Бозон. Частица с целым спином, равным 1, 2 и т. д. (одна из двух категорий частиц, допускаемых квантовой механикой; другой категорией является фермион). Примерами бозонов являются фотоны и хиггсовские частицы.
Брана. Мембраноподобный объект в многомерном пространстве, который может обладать энергией и удерживать частицы и взаимодействия.
Вакуум. Состояние Вселенной с наименьшей возможной энергией и без частиц.
Виртуальная частица. Эфемерная частица, допускаемая только законами квантовой механики; виртуальные частицы имеют тот же заряд, что и соответствующие реальные физические частицы, но неправильную энергию.
Внешние частицы. Реальные физические частицы, способные влетать в область взаимодействия и покидать ее.
Внутреннее вращение (спин). Число, характеризующее то, как ведет себя частица, которая как бы вращается. Спин может принимать как целые, так и полуцелые значения.
Внутренняя симметрия. Симметрия, в которой физические законы не меняются для множества преобразований, сохраняющих геометрическое положение частиц, но меняющих только некоторые внутренние свойства или метки.
Возмущение. Малая модификация известной теории.
Волновая функция. Квантово-механическая функция, определяющая относительную вероятность нахождения соответствующего объекта в любой точке пространства. -
Геодезическая. В пространстве — кратчайший путь между двумя точками; в пространстве-времени — путь свободно падающего наблюдателя (такого, на которого не действуют никакие силы).
Гиперкуб. Обобщение понятия куба на более чем три измерения.
Гипотеза пустыни. Предположение, что при энергиях ниже энергии объединения не могут рождаться никакие частицы кроме тех, которые включены в Стандартную модель.
Глубоко неупругое рассеяние. Эксперимент по рассеянию электронов на протонах и нейтронах, в котором были обнаружены кварки.
Глюон. Элементарная частица, переносящая сильное взаимодействие.
Горизонт. Область, из-под которой ничто не может вылететь.
Гравитационное линзирование. Расщепление луча света на множество изображений при огибании светом массивного тела.
Гравитино. Суперпартнер гравитона.
Гравитон. Частица, переносящая гравитационное взаимодействие.
ГэВ (гигаэлектронвольт). Единица энергии, равная одному миллиарду эВ.
Действие на расстоянии. Гипотетическое мгновенное влияние тел на другие удаленные тела.
Дуальные теории. Два эквивалентных описания одной и той же теории, которые могут казаться совершенно различными.
Закон обратных квадратов. Закон, описывающий те силы, напряженность которых уменьшается обратно пропорционально квадрату расстояния между объектами; классические гравитационное и электромагнитное поля подчиняются закону обратных квадратов.
Закон тяготения Ньютона. Классический закон тяготения, утверждающий, что сила притяжения между двумя массивными телами пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними.
Закрученная геометрия пространства-времени. Пространство-время (в общем случае каждый слой которого имеет одинаковую форму), которое было бы плоским, но закручивается благодаря присутствию общего масштаба, меняющегося в зависимости от положения в конкретном измерении.
Замкнутая струна. Струна, делающая петлю и не имеющая концов.
Излучение черного тела. Излучение, испускаемое черным телом.
Измерение. Независимое направление в пространстве или времени.
Инвариантность относительно вращений. Независимость результатов экспериментов от ориентации (или направления).
Инерциальная система отсчета. Система отсчета, движущаяся с постоянной скоростью по отношению к фиксированной, например покоящейся, системе отсчета.
Ион. Заряженное связанное состояние ядра и электронов; атом, в котором слишком мало, или слишком много электронов.
Калибрино. Суперпартнер калибровочного бозона, переносящего взаимодействие.
Калибровочный бозон. Частица, переносящая взаимодействие.
Калибровочная передача. Перенос нарушения суперсимметрии с помощью калибрино.
Квазикристалл. Твердое вещество, кристаллическая структура которого выводится из высших измерений.
Квант. Дискретная неделимая единица измеряемой величины; наименьшая единица этой величины.
Квантовый вклад. Вклад в физический процесс за счет виртуальных частиц.
Квантовая гравитация. Теория гравитации, объединяющая квантовую механику и общую теорию относительности.
Квантовая механика. Теория, основанная на предположении, что вся материя состоит из дискретных элементарных частиц, с которыми связаны волновые функции.
Квантовая теория поля. Используемая для изучения физики частиц теория, с помощью которой можно рассчитать вероятности процессов, в которых частицы могут взаимодействовать, рождаться или уничтожаться. Согласно квантовой теории поля, флуктуации полей проявляются как частицы.
Кварк. Элементарный фермион, испытывающий сильные взаимодействия.
Кварк «верхний» (u-кварк). Один из элементарных кварков, входящих в состав протона и нейтрона.
Кварк «боттом» (b-кварк). Короткоживущая и более тяжелая версия нижнего кварка (d-кварка) и «странного» (s-кварка).
Кварк «нижний» (d-кварк). Один из элементарных кварков, входящих в состав протона и нейтрона.
Кварк «очарованный» (с-кварк). Короткоживущая и более тяжелая версия верхнего кварка (u-кварка).
Кварк «странный» (s-кварк). Короткоживущая и более тяжелая версия u-кварка.
Кварк «топ» (t-кварк). Короткоживущая и более тяжелая версия u-кварка; самый тяжелый из всех известных кварков.
Кинетическая энергия. Энергия, связанная с движением.
Киральность. Спиральность частицы со спином.
Классическая физика. Законы физики, не принимающие во внимание ни квантовой механики, ни теории относительности.
Коллайдер частиц. Ускоритель частиц высоких энергий, на котором происходит столкновение частиц, сопровождаемое выделением огромной энергии.
Коллапс волновой функции. Редукция квантового состояния, после того как точное измерение фиксирует значение измеряемой величины.
Компактное пространство. Конечное (финитное) пространство.
Компактифицированное пространство. Пространство, скрученное в область конечных размеров.
Комптоновское рассеяние. Рассеяние фотонов на электронах.
Константа связи. Число, определяющее интенсивность взаимодействия.
Константа связи струны. Величина, определяющая интенсивность взаимодействия между струнами.
Космологическая постоянная. Значение постоянной фоновой плотности энергии, которая не переносится веществом.
Космология. Наука об эволюции Вселенной.
Красное смещение. Уменьшение частоты волны в том случае, когда излучающее волну тело либо удаляется (эффект Доплера), либо тормозится сильным гравитационным полем (гравитационное красное смещение).
Кривизна. Величина, описывающая искривление или изгибание объекта, пространства или пространства-времени.
КХД (квантовая хромодинамика). Квантово-полевая теория сильных взаимодействий.
КЭД (квантовая электродинамика). Квантово-полевая теория электромагнетизма.
Лептон. Элементарный фермион, не испытывающий сильного взаимодействия.
Локальное взаимодействие. Взаимодействие между соседними или совпадающими объектами.
Локализованная гравитация. Высокая концентрация гравитационного поля в определенной области пространства; гравитация, которая кажется низкоразмерной, так как она не растворена в дополнительных измерениях.
Локально локализованная гравитация. Теория, в рамках которой четырехмерная гравитация испытывается не везде, а только в области пространства, где сконцентрирована функция вероятности частицы, действующей как четырехмерный гравитон.
Матричная теория. Десятимерная квантово-механическая теория, которая, возможно, эквивалентна теории струн.
Метрика. Величина или величины, устанавливающие шкалу измерений, определяющую физические расстояния и углы.
Механизм Хиггса. Спонтанное нарушение электрослабой симметрии, которое позволяет приобрести массу калибровочным бозонам и другим элементарным частицам.
Мир на бране. Физическая структура, в которой материя и взаимодействия прикреплены к бранам.
Многообразие Калаби — Яу. Шестимерное компактное пространство, определяемое своими математическими свойствами и играющее важную роль в теории струн.
Модель. Кандидат в теорию.
Мода Калуцы — Клейна (КК). Четырехмерные частицы многомерного происхождения; КК-моды различаются своими импульсами в пространстве дополнительных измерений.
Молекула. Связанное состояние двух или нескольких атомов, в котором электроны распределяются между ними.
Мультивселенная. Гипотетическое обобщение Вселенной, содержащее области, не взаимодействующие или чрезвычайно слабо взаимодействующие друг с другом.
Мысленный эксперимент. Воображаемый физический эксперимент, с помощью которого можно оценить следствия данного набора физических предположений.
Мюон. Короткоживущий более тяжелый вариант электрона.
Натяжение. Сопротивление растяжению, определяющее, насколько просто будет колебаться струна, порождая тяжелые частицы.
Нейтральный объект. Объект, безразличный к взаимодействию; нейтральные объекты обладают нулевым полным зарядом.
Нейтрино. Фундаментальная элементарная частица, взаимодействующая только за счет слабого взаимодействия.
Нейтрон. Составная часть атомного ядра, в которой тесно связаны «-кварк и два й-кварка.
Нуклон. Протон или нейтрон.
Ньютоновская гравитационная постоянная. Общий коэффициент, определяющий силу гравитационного притяжения в законе тяготения Ньютона; эта постоянная обратно пропорциональна квадрату планковского масштаба масс.
Общая теория относительности. Теория тяготения, описывающая гравитационное поле, порождаемое любым источником материи или энергии, в том числе, запасенной самим гравитационным полем, в любой системе отсчета; согласно общей теории относительности гравитационное поле сосредоточено в кривизне пространства-времени.
Открытая струна. Струна с двумя концами.
Поле. Физическая сущность, имеющая определенные значения в каждой точке пространства. Примеры включают классическое электрическое поле и квантовые поля.
Проблема аромата (в суперсимметрии). Предсказание слишком высокого значения вероятности процессов с изменением аромата (за счет виртуальных скварков и слептонов), являющееся бедствием для большинства моделей нарушения суперсимметрии.
Поколение. Каждый из трех наборов частиц, содержащих полный комплект типов частиц (левый и правый заряженный лептон, верхний кварк и нижний кварк и левое нейтрино).
Проблема иерархии. Вопрос о слабости гравитации или, эквивалентно, вопрос о том, почему планковский масштаб масс, характеризующий интенсивность гравитационного взаимодействия, на шестнадцать порядков величины больше, чем масштаб массы слабых взаимодействий, связанный со слабым взаимодействием.
Промежуточные (внутренние) частицы. Виртуальные частицы, обмен которыми переносит взаимодействия между другими частицами.
Продольная поляризация. Колебания волны вдоль направления движения.
Планковский масштаб длины. Масштаб длины, на котором гравитация сильна, и в предсказания гравитационных эффектов следует включить квантовые эффекты.
Планковский масштаб энергий. Энергия, при которой гравитация становится сильным взаимодействием, и необходимо учитывать квантово-механические вклады.
Позитрон. Положительно заряженная античастица электрона.
Поляризация. Направление колебаний волны.
Поперечная поляризация. Колебание волны, перпендикулярное направлению распространения.
Постоянная Планка. Квантово-механическая величина, связывающая энергию с частотой и импульс с длиной волны.
Потенциальная энергия. Запасенная энергия, которая может быть высвобождена в форме кинетической энергии.
Преобразование симметрии. Манипуляция с физической системой, не меняющая ее свойства или поведение; действие, преобразующее различные конфигурации, связанные друг с другом симметрией.
Принцип Паули. Утверждение, что два тождественных фермиона не могут занимать одно и то же место.
Принцип эквивалентности. Принцип, согласно которому однородное ускорение неотличимо от тяготения.
Проекция. Определенное предписание для получения представления меньшей размерности для объекта более высокой размерности.
Протон. Составная часть атомного ядра, в котором два u-кварка и один d-кварк сильно связаны друг с другом.
Пространство-время. Концепция, объединяющая пространство и время в единую структуру; математическая формулировка области, где могут происходить физические процессы.
Пространство анти-де Ситтера. Пространство-время с постоянной отрицательной кривизной.
Пространство де Ситтера. Пространство-время постоянной положительной кривизны.
Размерность. Число величин, требуемых для однозначного определения положения точки.
Размерность браны. Число измерений, по которым разрешено перемещаться связанным на бране частицам.
Ренормализационная группа. Техника вычислений для нахождения связи между величинами, которые относятся к разным энергетическим или пространственным режимам.
Свободная от аномалий теория. Теория, в которой симметрии классической теории являются также симметриями теории с учетом квантовых вкладов.
Семейство. См. поколение.
Сильное взаимодействие. Одно из четырех известных взаимодействий; например, сильное взаимодействие ответственно за связывание кварков в протоне или нейтроне.
Симметрия. Свойство объекта или физического закона, состоящее в том, что некоторые физические операции являются недетектируемыми.
Симметрия ароматов. Симметрия, меняющая местами различные ароматы из конкретной категории частиц.
Сингулярность. Область, в которой разрушается математическое описание объекта, так как некоторая величина становится бесконечной.
Система отсчета. Наблюдательная точка отсчета или множество координат для описания событий в пространстве или пространстве-времени.
Скварк. Суперпартнер кварка.
Скорость. Величина, характеризующая одновременно модуль скорости и ее направление.
Слабое взаимодействие. Одно из четырех известных взаимодействий; например, слабое взаимодействие ответственно за бета-распад нейтронов в протоны.
Слабые взаимодействия, масштаб длины Длина 10-16 см, которая соответствует (по законам квантовой механики и специальной теории относительности) масштабу энергии слабых взаимодействий. Это есть радиус действия слабого взаимодействия, т. е. максимальное расстояние между частицами, на котором они могут влиять друг на друга путем слабого взаимодействия.
Слабые взаимодействия, масштаб массы. Масса, связанная с масштабом энергии слабых взаимодействий (порядка 250 ГэВ) и скоростью света. В обычных массовых единицах масштаб масс слабых взаимодействий равен 10-21 г.
Слабые взаимодействия, масштаб энергии. Энергия, при которой спонтанно нарушается симметрия, связанная со слабым взаимодействием. Масштаб энергии слабых взаимодействий определяет массы элементарных частиц.
Слабый калибровочный бозон. Элементарная частица (существующая в трех разновидностях и Z), являющаяся переносчиком слабого взаимодействия.
Слептон. Суперпартнер лептона.
Соотношение неопределенностей. Основной принцип, составляющий фундамент квантовой механики, ограничивающий точность, с которой могут быть одновременно измерены пары величин (например, положение и скорость частицы).
Спектр. Функция, определяющая разброс энергии, излученной на всех частотах.
Спектральные линии. Дискретные частоты, на которых неионизированный атом испускает или поглощает свет.
Специальная теория относительности. Релятивистская теория, описывающая движение в инерциальных системах отсчета.
Спин. См. внутреннее вращение.
Спиральность. Направление спина (вращения) налево или направо.
Спонтанно нарушенная симметрия. Симметрия, которая сохраняется физическими законами, но нарушается реальным физическим состоянием системы.
Стандартная модель (в физике частиц). Эффективная теория, описывающая все известные частицы и негравитационные силы и взаимодействия между ними.
Старая квантовая теория. Предшественница квантовой механики, постулировавшая правила квантования, но не определявшая их систематически или не описывавшая эволюцию квантового состояния во времени.
Структура. Составные части материи.
Струна. Одномерный (в пространстве) протяженный объект, осцилляции которого образуют элементарные частицы.
Струя. Энергичный сгусток сильно взаимодействующих частиц, окружающий кварк или глюон большой энергии, движущийся в определенном направлении.
Субструктура. Более элементарные составные части структуры материи.
Супергравитация. Суперсимметричная теория, включающая гравитацию.
Суперпартнер (частицы). Частица, которая связана суперсимметрией с другой частицей; если исходная частица — бозон, суперпартнер — фермион, и наоборот.
Суперпространство. Абстрактное пространство, включающее знакомые четыре измерения, а также гипотетические фермионные измерения.
Суперсимметрия. Симметрия, меняющая местами пары бозонов и фермионов.
Сэлектрон. Суперпартнер электрона.
Тахион. Частица, сигнализирующая о нестабильности, и внешне проявляющаяся как частица с отрицательным квадратом массы.
Тау-лептон. Короткоживущая частица с таким же зарядом, как у электрона и мюона, но более тяжелая.
Темная материя. Несветящаяся материя, составляющая примерно 25 % всей энергии Вселенной.
Темная энергия. Измеренная энергия вакуума во Вселенной, составляющая 70 % всей энергии Вселенной, но не переносящаяся какой бы то ни было формой материи.
Теория. Определенный набор элементов и принципов, а также правил и уравнений для предсказания того, как эти элементы взаимодействуют друг с другом.
Теория Великого объединения (ТВО). Предполагаемая теория, в рамках которой три известные негравитационные взаимодействия сливаются при большой энергии в единое взаимодействие.
Теория возмущений. Когда интересующая вас теория отличается от решаемой (обычно не содержащей взаимодействия) теории малым параметром (это может быть, например, малая интенсивность взаимодействия), теория возмущений позволяет совершить экстраполяцию от решаемой теории к интересующей вас теории путем последовательного разложения по малому параметру. Результаты выражаются в виде разложений по степеням соответствующего параметра, являющегося обычно константой связи.
Теория гетеротических струн. Версия теории струн, в которой колебательные моды, распространяющиеся по часовой стрелке, отличаются от мод, распространяющихся против часовой стрелки.
Теория относительности. Одна из двух созданных Эйнштейном теорий пространства-времени: специальная теория относительности, объединившая пространство и время, и общая теория относительности, объясняющая тяготение как кривизну пространства-времени.
Теория струн. Теория, утверждающая, что составными частями Вселенной являются фундаментальные струны, которая должна согласованно включить квантовую механику и общую теорию относительности.
Теория суперструн. Суперсимметричный вариант теории струн без тахионов, включающий вдобавок к гравитонам и калибровочным бозонам еще и фермионы.
Теория Хоржавы — Виттена. Теория сильносвязанных гетеротических струн, или эквивалентно (по дуальности) версия теории струн с двумя бранами, разделенными одиннадцатым измерением, в котором спрятаны взаимодействия гетеротической струны.
Тонкая настройка. Манипуляция путем подгонки параметра к очень специальному (и маловероятному) значению.
Трансляционная инвариантность. Независимость физических законов от места в пространстве.
ТэВ (тераэлектронвольт). Единица энергии, равная одному триллиону эВ.
Тэватрон. Коллайдер высокой энергии, в настоящее время работающий в Фер-милабе; на этом коллайдере сталкиваются пучки протонов с энергией 1 ТэВ и пучки антипротонов такой же энергии.
Уединение. Физическая изоляция разных типов элементарных частиц в дополнительных измерениях.
Ультрафиолетовая катастрофа. Предсказываемая классической теорией черного тела бесконечная энергия, излучаемая при высоких частотах.
Уравнения Эйнштейна. Уравнения общей теории относительности, с помощью которых по заданному распределению материи и энергии определяется метрика (следовательно, гравитационное поле).
Ускоритель частиц. Установка для изучения физики высоких энергий, ускоряющая частицы до высоких энергий.
Фактор конформный. Общий масштаб метрики, зависящий в случае закрученной геометрии от координаты дополнительного измерения.
Фейнмановская диаграмма. Диаграмма, схематически изображающая разрешенные взаимодействия в физике частиц.
Ферми взаимодействие. Взаимодействие, порождаемое обменом одним из массивных слабых калибровочных бозонов.
Фермилаб. Ускорительный центр в штате Иллинойс (США). В этом центре находится Тэватрон.
Фермион. Частица с полуцелым спином 1/2, 3/4 и т. д. (одна из двух категорий частиц, допускаемых квантовой механикой; другой категорией является бозон). Примерами фермионов служат кварки и лептоны.
Физика частиц. Раздел физики, изучающий самые фундаментальные строительные блоки материи.
Фотино. Суперпартнер фотона.
Фотон. Элементарная частица, осуществляющая передачу электромагнитного взаимодействия; квант света.
Функция вероятности. Квадрат модуля волновой функции, определяющий вероятность обнаружения частицы в данном месте.
Хиггсовское поле. Поле, участвующее в механизме Хиггса, ответственном за нарушение симметрии, связанной с электрослабым взаимодействием.
ЦЕРН. Вошедшая в обиход аббревиатура, построенная по первым латинским буквам названия Европейской организации ядерных исследований (Conseil Européen pour la Recherche Nucléaire — CERN) в Женеве (Швейцария). ЦЕРН является международным ускорительным центром высоких энергий, где в ближайшее время вступит в строй Большой адронный коллайдер (БАК) — самый мощный ускоритель на встречных пучках протонов.
Черная дыра. Компактный объект, который настолько плотен, что ничто не может вырваться из окружающего этот объект гравитационного поля.
Черное тело. Идеализированое тело, поглощающее всю теплоту и энергию и излучающее ее по закону, определяемому только температурой.
эВ (электронвольт). Энергия, требуемая для преодоления электроном разности потенциалов 1 В.
Электромагнетизм. Одно из четырех известных взаимодействий; электромагнетизм совместно описывает электричество и магнетизм.
Электрон. Очень легкая элементарная частица с отрицательным зарядом.
Электрослабая теория. Теория, включающая как электромагнитное, так и слабое взаимодействие; существенный компонент Стандартной модели физики частиц.
Энергия вакуума. Энергия, которой обладает вакуум; состояние, в котором отсутствуют частицы; также известна как космологическая постоянная.
Эфир. Гипотетическая невидимая среда (в наши дни полностью развенчанная), колебания которой, как считалось, являются электромагнитными волнами.
Эффективная теория. Теория, описывающая те элементы и взаимодействия, которые в принципе наблюдаемы на расстоянии или в масштабе энергий, выше которых она применима.
Эффективная теория поля. Квантовая теория поля, определенная при некоторой энергии и описывающая те частицы и взаимодействия, которые относятся к энергиям, при которых эта теория применима.
Ядро. Твердый, плотный центральный компонент атома.
D — брана. В теории струн брана, на которой заканчиваются открытые струны.
М-теория. Гипотетическая всеобъемлющая теория, объединяющая все известные версии десятимерной теории струн и одиннадцатимерной супергравитации.
р-брана. Решение уравнений тяготения Эйнштейна, продолжающееся бесконечно далеко в некоторых пространственных измерениях, но в оставшихся измерениях ведущее себя как черная дыра, захватывающая слишком близко подошедшие тела.
T-дуальность. Эквивалентность между физическими явлениями во вселенной с малым скрученным измерением и другой вселенной с большим измерением (величина радиуса свернутого измерения заменяется на обратную величину).
Математические примечания
1. Это замечание на самом деле не математическое, но «мальчик субботнего вечера» трехмерен (рис. M1).

2. Метрика пространства может иметь вид
ds2 — ах dx2 + ау dy2 + az dz2,
где x,y,z — три координаты точки в пространстве, ах, ау, az могут быть числами или функциями от х, у, z. Метрика определяет длины, расстояния и углы между прямыми. Например, длина вектора, исходящего из начала координат в точку с координатами {х, у, z}, равна
(ахх2 + ауу2 + azz2)1/2.
Если ax= ay = az = 1, это соответствует плоскому пространству, так что расстояния и длины будут измеряться обычным способом. Например, длина вектора, исходящего из начала координат в точку {х, у, z}, будет равна (х2 + у2 + z2)1/2.
В более сложных метриках могут появляться перекрестные члены типа dxdy. В этом случае метрика должна описываться тензором с двумя индексами, которые определяют коэффициенты aij каждого слагаемого метрики вида dxi dxj. Позднее, при обсуждении теории относительности, у метрики появится слагаемое dt2, а также возможные слагаемые вида dt dxi.
3. Гиперсфера определяется уравнением
x12 + x22 +… + xn2 = r2
Здесь xiобозначает i-ю координату (местоположение в i-м измерении), а r есть радиус гиперсферы. Сечение гиперсферы, когда она пересекает фиксированное положение в п-м измерении xn = d, описывается уравнением
x12 + x22 +… + xn — 12 = r2 - d2
Это уравнение гиперсферы, размерность которой на единицу меньше, а радиус равен (г2 — d2)1/2. Так, например, когда п = 3 и сфера пересекает Флатландию, ее жители флатландцы будут видеть окружности. (Они будут видеть диски, если будут смотреть на окружности и на то, что внутри этих окружностей, что математически описывается неравенством.)
4. Многообразия Калаби — Яу не являются единственными скрытыми многообразиями в теории струн. Сейчас мы знаем, что и другие многообразия, например, многообразия, называемые (G2-голономными, могут приводить к приемлемым моделям.
5. В теории струн мы также иногда используем слово «брана» для обозначения заполняющих пространство бран, имеющих то же число измерений, что и многомерное пространство. Однако здесь мы сосредоточимся только на бранах, имеющих меньшее число измерений, чем полное многомерное пространство, так что я ограничусь использованием термина так, как описано в книге.
6. Брана, простирающаяся вдоль измерений х1….,xj, описывается п — jуравнениями
xj + 1 = cj + 1, xj + 2 = cj + 2…, xn = cn
где xi — координаты, п — число измерений пространства, а сi — фиксированные константы, описывающие положение браны. Более сложные браны, которые искривлены в данной системе координат, описываются более сложными уравнениями, описывающими поверхность.
7. В форме уравнения закон Ньютона утверждает, что сила тяготения равна
Gm1m2/r2
где G — ньютоновская постоянная, m1 и m2 — две массы, которые притягиваются друг к другу, а r — расстояние между ними.
8. Ньютоновское тяготение согласуется с евклидовой геометрией. В евклидовой геометрии длина вектора, проведенного в точку с координатами (х, у, z), равна (х2 + у2 + z2)1/2 и не зависит от системы координат. Это означает, что вы можете вращать вашу систему координат, но расстояние до любой точки не будет меняться, даже если будут меняться отдельные координаты. Специальная теория относительности вводит в эту картину время. Она утверждает, что х2 + у2 + z2 — c2-t2 не зависит от вашего выбора инерциальной системы отсчета. Заметим, что эта инвариантная величина включает и пространство, и время, но время рассматривается иначе из-за знака минус перед слагаемым c2t2. Заметим также, что для того, чтобы эта величина не зависела от выбора инерциальной системы, изменения системы отсчета должны перемешивать значения пространственных и временных координат. Если одна система отсчета движется со скоростью v по отношению к другой в направлении вдоль оси х, преобразования координат от (t, х, у, z) к (t', х', у', z') будут иметь вид
х' = γх — cβγt, t' = γt — βγx/c, у' = у, z' = z,
с
где β — v/c, с — скорость света, γ = (1 — β2)-1/2.
9. Уравнения Эйнштейна указывают нам, как определить метрику gμν по известному распределению материи и энергии:
Rμν = 1/2gμνR = 8πG/c4*Tμν
Здесь Rμν — тензор кривизны Риччи, связанный с метрикой gμν — тензор энергии-импульса, описывающий распределение материи и энергии, G — ньютоновская постоянная тяготения, с — скорость света. Например, для покоящегося вещества плотностью массы ρ компонента T00 = ρ, в то время как все другие компоненты тензора равны нулю.
10. Энергия на единичный интервал частоты, излучаемая черным телом температурой Т зависит от частоты f согласно формуле f3/(еhf/kT — 1), где k = 1,3807 — 10-16 эрг/К — постоянная Больцмана, переводящая температуру в энергию. Обратите внимание на то, что при низких частотах энергия растет с частотой. Однако при частотах, когда энергия кванта hf велика по сравнению с kT, спектр резко обрывается, и излучаемая энергия при больших частотах экспоненциально мала.
11. На самом деле волновая функция является комплекснозначной. Это является источником многих странных свойств квантовой механики. Когда вы складываете две комплексные функции, а затем возводите сумму в квадрат, вы в общем случае получите результат, отличный от того, который получится, если сначала возвести в квадрат, а затем сложить. Это приводит к явлениям интерференции. Например, в эксперименте с двумя щелями вероятность, записанная на экране, возникает от интерференции волн, описывающих два возможных пути электрона.
12. Точнее, это есть произведение постоянной Планка и абсолютной величины коммутатора двух величин, деленной пополам.
13. Специальная теория относительности утверждает, что покоящееся тело массой m0обладает энергией Е = m0c2. В более общем случае, тело, движущееся со скоростью v (β = v/с, γ = (1 — β2)-1/2), переносит энергию Е = γт0с2. Массу т0 иногда называют инвариантной массой (т. е. не зависящей от системы отсчета). Это название связано с тем, что согласно законам преобразования специальной теории относительности соотношение
Е2 — р2с2 = (m0)2с4
одинаково в любой системе отсчета. Заметим, что для того, чтобы породить тело массой то, необходимо затратить энергию, по меньшей мере равную m0c2. Обратим внимание также на то, что когда масса тела мала по сравнению с его энергией (на самом деле, с энергией, деленной на с2), энергия и импульс связаны приближенным соотношением Е = рс. Именно поэтому при высокой энергии импульс и энергия взаимозаменяемы.
14. Уравнения Максвелла в системе СГСЭ имеют вид:
div Е = 4πρ,
rot E = — 1/c * ϐB/ϐt
div В = 0,
rot H = 4π/c * j + 1/c * ϐE/ϐt
где Е — электрическое поле, В — магнитное поле, ρ — плотность заряда, j — плотность тока. Это дифференциальные уравнения первого порядка; комбинируя два их них, можно вывести дифференциальное уравнение второго порядка, включающее только электрическое или только магнитное поле. Это уравнение принимает вид волнового уравнения, т. е. его решения есть синусоидальные волны[188].
15. На самом деле, согласно основополагающим принципам специальной теории относительности, может быть и четвертая поляризация, которая соответствует колебаниям во временном измерении. Но она тоже не существует, и та же внутренняя симметрия, которая устраняет третью (продольную) поляризацию, устраняет и «временную поляризацию». Так как эти вопросы не играют роли в обсуждении в этой и последующей главах, мы не будем их далее рассматривать.
16. На самом деле истинные симметрии, связанные со всеми взаимодействиями, более тонки и поворачивают поля, являющиеся комплексными величинами, превращая их друг в друга. Симметрии не только меняют поля местами, они превращают одно поле в линейную суперпозицию других полей. Взаимодействие, связанное с электромагнетизмом, поворачивает одно комплексное поле, в то время как слабое взаимодействие вращает два комплексных поля, превращая их друг в друга, а сильное взаимодействие вращает три поля.
17. Чтобы модель Хиггса заработала, нужно сделать так, чтобы по крайней мере одно из хиггсовских полей приняло ненулевое значение. Это станет возможным, если возникнет конфигурация с минимальной энергией, в которой значение по крайней мере одного из хиггсовских полей не равно нулю. Один из способов сделать это продемонстрирован на рис. М2, на котором показан так называемый потенциал «Мексиканская шляпа», т. е. график энергии, которую примет система для любой комбинации значений двух хиггсовских полей, причем две нижние оси являются абсолютными значениями двух хиггсовских полей, а высота трехмерной поверхности представляет энергию данной конкретной конфигурации. Этот конкретный потенциал имеет вид

λ(│H1│ + │H2│ — v2 )2 ,
где λ определяет то, как искривлен потенциал, а V определяет значение, которое принимает │H1│ + │H2│ в точке минимума потенциала. Ключевое свойство этого потенциала заключается в том, что когда оба поля имеют равные нулю значения, это соответствует локальному максимуму. Поэтому энергетические соображения говорят, что оба хиггсовских поля не могут быть равными нулю. Напротив, они примут такие значения, которые поместят их на дно круговой чаши, окружающей начало координат.
18. Более точный способ описания симметрии слабого взаимодействия состоит в том, чтобы сказать, что она вращает поля, а не меняет их местами.
19. Это действительно упрощает нарушение симметрии. Даже, если х и у оба не равны нулю, например, если х и у равны 5, вращательная симметрия будет нарушена, так как выбрано конкретное направление, указывающее направление от точки x = 0, у = 0 к точке x = 5, у — 5. Аналогичная «вращательная» симметрия применима к полям хиггс1 и хиггс2, но я упростила рассмотрение и рассматриваю симметрию просто как обменную. В действительности, даже если оба хиггсовских поля примут одинаковые значения, симметрия слабого взаимодействия будет нарушена, во многом аналогично тому, как точка х = 5, у = 5 спонтанно нарушает вращательную симметрию.
20. Хотя построение этой модели начинается с двух комплексных хиггсовских полей, в конечном итоге остается одна хиггсовская частица. Это происходит потому, что три остальных (действительных) поля становятся тремя дополнительными полями, требуемыми для того, чтобы превратить три безмассовых частицы с двумя физическими поляризациями в массивные частицы с тремя поляризациями. Три хиггсовских поля становятся третьими поляризациями трех тяжелых слабых калибровочных бозонов — двух W и Z. Четвертое оставшееся хиггсовское поле должно рождать истинные физические хиггсовские частицы. Если такая модель верна, эти частицы должны родиться на БАК.
21. Интенсивность каждого взаимодействия определяется численным коэффициентом (константой взаимодействия). Вычисления методом ренормализационной группы показывают, что значения этих констант логарифмически меняются с энергией.
22. В то время как симметрия слабого взаимодействия смешивает пары полей, а симметрия сильного взаимодействия смешивает три поля, группа симметрии теории Великого объединения Джорджи — Глэшоу смешивает пять полей. Некоторые преобразования симметрии, связанные с взаимодействиями ТВО, совпадают с преобразованиями слабой и сильной симметрии. Взаимодействия объединяются, так как одна единственная группа преобразований симметрии включает все преобразования симметрии Стандартной модели.
23. Эта связь с пространством и временем становится на самом деле более явной, если последовательно совершаются два преобразования суперсимметрии, сначала в одном порядке, а затем в другом, после чего один результат вычитается из другого. В этом случае фермионы остаются фермионами, а бозоны бозонами, но система совершает движение; окончательный результат преобразования в точности тот же, как и обычное преобразование пространства-времени. Коммутатор двух суперсимметричных преобразований, осуществляющий точно ту же операцию, как и единственное преобразование пространственно-временной симметрии, убедительно демонстрирует, что преобразования суперсимметрии должны быть связаны с симметриями, которые действуют на пространство и время и передвигают вещи.
24. Траектория частицы — это мировая линия, определяющая положение частицы как функцию времени. Траектория струны — это поверхность, описывающая положение всей струны в процессе ее движения во времени. Мировая поверхность представляет движение открытой струны, а мировая трубка представляет движение замкнутой струны.
Это показано на рис. М3, где иллюстрируется движение во времени и «более мягкие» взаимодействия струн.
25. Натяжение струны не всегда так велико, как можно подумать, зная значение планковского масштаба энергии. Оно зависит от того, насколько сильно взаимодействуют струны. Джо Ликкен и др. рассматривали возможность, что оно намного меньше, и в этом случае дополнительные частицы в теории струн могли бы быть намного легче.
26. На самом деле, согласно принципу дуальности, о котором шла речь в этой главе, даже пробные частицы, используемые для изучения данной версии теории струн, изменяют свой характер, когда связь становится сильной. Так, если Икар действительно был частью струнного мира, он также изменился бы.
27. Они могут простираться и в нулевом измерении, тогда они являются новыми типами частиц, которые называются D0-бранами, а также в одном измерении, и тогда возникают новые типы струн, называемые D1 — бранами.
28. Браны не обязательно взаимодействуют посредством обычных зарядов. Они взаимодействуют посредством многомерных обобщенных зарядов.
29. На самом деле симметрия вращает браны, переводя их друг в друга, но это находится за рамками технического уровня этой книги.
30. Обычно массы калибрино находятся в отношении 1:3:30, причем фотино является самой легкой частицей, следующими идут вино (хотя зино могут быть немного тяжелее или легче, чем вино), а глюино — самые тяжелые. В уединенных моделях это отношение равно 1:2:8, причем вино — самые легкие, фотино тяжелее, а глюино опять самые тяжелые.
31. Волновые функции мод Калуцы — Клейна — это те моды, которые возникают в обобщенном фурье-разложении многомерной волновой функции.
32. Это предполагает также, что в геометрии пространства-времени отсутствуют сингулярности, т. е. места, где пространство-время сжимается до нулевого размера.
33. Д. Кремадес, С. Франко, Л. Ибаньес, Ф. Марчесано, Р. Рабадан и А. Уранга предложили интересную альтернативу. Их идея состоит в том, что частицы закреплены не на индивидуальных бранах, а на пересечениях разных бран. Как и в случае разделенных параллельных бран, простирающиеся между бранами струны должны быть в общем случае тяжелыми. Но легкие или безмассовые частицы возникают от струн нулевой длины, которые в этом случае были бы прикреплены к области, где происходит пересечение бран.
34. Мы можем также показать это несколько иным способом с помощью более математизированного рассуждения. Когда имеются свернутые измерения, силовые линии, исходящие от массивного объекта, ведут себя на малых расстояниях согласно закону тяготения в пространстве с большим числом измерений, а на больших расстояниях — согласно четырехмерному закону тяготения. Единственный способ согласовать два закона силы и гладко переключиться от одного к другому состоит в том, чтобы заметить, что на расстояниях, примерно соответствующих размерам дополнительных измерений, силовые линии расходятся так, как будто существуют только четыре измерения, но с интенсивностью, подавленной за счет дополнительного объема свернутого пространства. За пределами размера дополнительных измерений гравитация ведет себя четырехмерно, но с интенсивностью, подавленной за счет размытия по объему дополнительных измерений.
Ньютоновский закон тяготения утверждает, что когда имеются три пространственных измерения, сила пропорциональна
1/MPl2 x 1/r2
Если существуют п дополнительных измерений, то закон силы примет вид
1/Mn+2 x 1/rn+2
где М определяет интенсивность тяготения в пространстве большего числа измерений, аналогично тому, как МPl определяет интенсивность четырехмерной гравитации. Заметим, что силовой закон в пространстве с дополнительными измерениями быстрее меняется как функция r, так как силовые линии расплываются по гиперсфере, поверхность которой имеет п + 2 измерения (в противоположность двумерной поверхности сферы, определяющей закон тяготения в трехмерном пространстве). Однако, когда объем дополнительных измерений конечен и п дополнительных измерений имеют размер R, закон силы примет вид
1/Mn+2 x 1/rn x1/r2
где r больше R, и силовые линии не могут более распространяться в дополнительных измерениях. Если осуществить отождествление МPl2 = Мп+2Rn, то это будет форма пространственно трехмерного закона силы. Так как Rп есть объем пространства дополнительных измерений, мы получаем, что интенсивность гравитационного взаимодействия уменьшается с объемом, или, что эквивалентно (так как интенсивность тяготения слабее, когда планковский масштаб энергии больше), планковский масштаб энергии большой, если объем большой.
35. Плоская метрика с тремя пространственными измерениями имеет вид
ds2 = dx2 + dy2 + dz2 — с2dt2.
Так как в ней нет никаких коэффициентов, зависящих от пространственных или временной переменных, измерения не зависят от того, где вы находитесь или в каком направлении смотрите. Можно сказать, что пространство-время полностью плоское. Все три пространственные координаты, а также временная координата (с точностью до знака минус, который всегда выделяет время) рассматриваются на равных основаниях. Это означает, что коэффициенты в слагаемых метрики полностью не зависят от положения во времени и пространстве.
36. Метрика закрученной геометрии имеет вид
ds2 = е -k|r| (dx2 + dy2 + dz2 — с2dt2) + dr2,
где г — координата пятого измерения. Это говорит нам о том, что при любом фиксированном положении в пятом измерении, соответствующем фиксированному значению г, пространство-время полностью плоское. Однако общий зависящий от г множитель указывает, что способ измерения размера меняется в соответствии с положением объекта в пятом измерении. Экспоненциальное уменьшение коэффициента, являющегося закручивающим конформным фактором, есть причина того, что функция вероятности гравитона экспоненциально уменьшается, а также того, почему мы должны менять масштаб массы, энергии и размера, чтобы получить единую четырехмерную эффективную теорию.
37. Так как пространство не является плоским, объем дополнительных измерений, возникающий при вычислении MPl в четырех измерениях, не равен просто MPl3R, как это было бы в случае плоского пространства. Теперь значение MPl зависит от кривизны. Если метрика имеет форму
ds2 = е -k|r| (dx2 + dy2 + dz2 — с2dt2) + dr2
где r — координата пятого измерения, то, приблизительно, MPl2 = М3/k. Иными словами, размер пространства в значительной степени безразличен. Это разумно, так как кривизна пространства, а не размер дополнительного измерения, определяет то, каким образом силовые линии распространяются в дополнительном измерении, и тем самым определяют интенсивность четырехмерной гравитации. На самом деле существует небольшая зависимость от R. Правильная формула имеет вид
MPl =M3 / k(1 — e-kR),
но когда kR велико, экспоненциальное слагаемое практически не существенно, и им можно пренебречь.
38. Закручивающий фактор в локально локализованной модели гравитации, которую предложили Андреас Карч и я, есть сумма уменьшающейся экспоненциальной функции (как в закрученных геометриях, которые мы уже рассматривали) и растущей экспоненциальной функции. Этот фактор пропорционален ch (kc — k|r|), где величина k связана с энергией балка, а величина с — с энергией браны. Аналогично закручивающему фактору локализованной гравитации, который мы уже рассматривали, этот закручивающий фактор экспоненциально уменьшается, если вы покидаете брану. Но в противоположность предыдущему случаю, закручивающий фактор резко меняет поведение и экспоненциально возрастает. Четырехмерный гравитон локализован в области между браной и этой «точкой разворота». Вне этого расстояния четырехмерная гравитация более неприменима.
39. При преобразовании T-дуальности радиус компактификации r меняется со своим обратным 1/r (расстояния при этом измеряются в единицах длины струны).
40. Однако физики Чаба Чаки, Джошуа Эрлих и Кристоф Грожан сделали интересное наблюдение, что скорость света и скорость гравитации могут различаться (в действительности скорость распространения гравитации может быть больше), если существует асимметрично закрученное пространство-время, в котором масштабы временной и пространственных координат вдоль пятого измерения отличаются друг от друга.